极软岩巷道钢管混凝土支架结构优化设计*

何晓升于广龙孙晓彤杨永迁

（1.中国矿业大学（北京）力学与建筑学院，北京市海淀区，100083；2.冀中能源股份有限公司，河北省邯郸市，056107）

极软岩巷道钢管混凝土支架结构优化设计*

何晓升1于广龙2孙晓彤1杨永迁2

（1.中国矿业大学（北京）力学与建筑学院，北京市海淀区，100083；2.冀中能源股份有限公司，河北省邯郸市，056107）

为解决查干淖尔一号井回风大巷钢管混凝土支架反底拱失稳破坏问题，分析了支架变形破坏原因。采用结构力学分析方法，研究了拱脚固支约束受均布荷载作用下的钢管混凝土圆弧拱内力大小随矢跨比变化的规律。理论计算结果表明：当圆弧拱矢跨比小于0.25时，在一定的均布荷载作用下，ø194 mm×10 mm钢管混凝土支架反底拱随着矢跨比的增加，拱内最大轴力与最大弯矩下降明显，因此反底拱矢跨比0.25～0.3较为合理。优化方案将反底拱矢跨比为0.15的钢管混凝土支架改为反底拱矢跨比为0.25的支架，其他措施与原有支护方案相同。巷道返修完成2年后无明显变形。

极软岩巷道 钢管混凝土支架 结构设计 矢跨比

钢管混凝土支架作为一种新型高承载力支架，每米含钢量相同的条件下，支架承载力可达U型钢支架的2～3倍，可为巷道提供强大的支护反力。该种支架已在我国20余个矿井的深埋巷道和软岩巷道中使用，取得了良好的应用效果，钢管混凝土支架为巷道支护提供了一种新的支架形式。

目前，对钢管混凝土支架的应用研究主要在于利用其自身承载能力大，且一定塑性变形范围内，承载力不下降的特点，运用基于钢管混凝土支架的复合支护方案控制巷道围岩的变形。

查干淖尔一号井井底车场巷道顶底板极软岩层厚度达42 m，可锚性差，锚杆、锚索支护作用有限。巷道开挖后的半年内，虽先后采用29U型钢支架+锚网喷支护、16#对工字钢棚+锚网喷支护和36U型钢支架+锚网喷支护返修巷道，均未能实现巷道长期稳定。

2012年3月起，查干淖尔一号井井底车场采用基于钢管混凝土支架的复合支护技术进行返修巷道长度达609 m，巷道实现了长期稳定，支护效果良好。然而，距回风大巷起点174.5～194.5 m段长度20 m巷道采用基于钢管混凝土支架复合支护方案返修巷道2个月后，底板混凝土在巷道底角处突然开裂，巷道变形不断扩展，至8月11日12时，巷道收敛速度突然加快，至15时，巷道底鼓量达2.7 m。

本文对原有支护中的钢管混凝土支架反底拱进行了结构力学分析，发现反底拱的矢跨比对支护结构的承载能力影响较大，给出了反底拱合理的矢跨比范围。在支护材料不变的条件下，仅增加了支架反底拱矢跨比，优化了支架受力情况，提出了返修方案。巷返修道已有2年，巷道稳定性良好。

1　工程概况

查干淖尔一号井井底车场回风大巷位于2#煤层底板泥岩中，距回风大巷起点174.3 m处，巷道完全进入断层破碎带，巷道实测剖面与局部放大如图1所示。

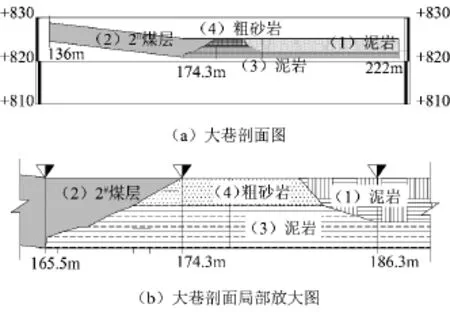
图1　回风大巷所在的断层破碎带

2#煤层顶底板中极软弱岩层厚度达42 m，单轴抗压强度均低于3.79 MPa，围岩含水状态接近饱和，属于极软岩巷道。钻孔岩土试验参数及岩性见表1。

表1　岩土试验参数

2　巷道原有支护情况

原有钢管混凝土支架支护断面如图2所示，基于钢管混凝土支架的复合支护方案为:

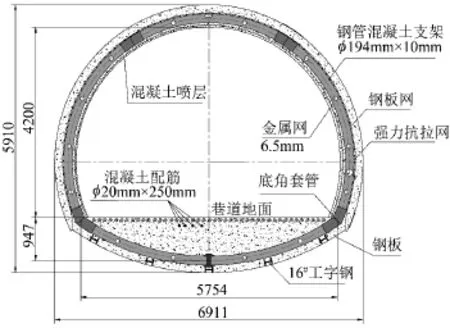
图2　钢管混凝土支架支护断面图

临时支护:50 mm厚混凝土喷层；

永久支护:ø194 mm×10 mm钢管混凝土支架+400 mm厚混凝土喷层。钢管混凝土支架钢管型号为ø194 mm×10 mm，支架间距0.7 m，支架内灌注C40混凝土。

施工工艺:

（1）巷道地面以下，铺设5 mm厚钢板和16#工字钢，安装支架反底拱段及支架间顶杆。

（2）巷道地面以上，钢管混凝土支架壁后挂强力抗拉网和钢板网，强力抗拉网横筋直径18 mm，纵筋直径8 mm，网格规格250 mm×150 mm（宽×高），钢板网网孔为菱形，网孔尺寸25 mm× 25 mm，支架内侧挂钢筋网，规格200 mm× 200 mm，支架壁后木板背实。每安装两架支架以C40混凝土浇筑巷道地坪，底板混凝土配直径20 mm钢筋，间距250 mm。铺设轨道方便运料与施工。

（3）支架安装完成15架后集中灌注钢管混凝土支架。

（4）最后，已灌注混凝土支架处施工喷射混凝土，混凝土强度C20。

施工完成约3月后，回风大巷174.5～194.4 m段底板混凝土在巷道右侧底角处混凝土突然开裂，且底板裂缝不断扩展，又经过一周缓慢变形后，巷道变形速度突然加快，造成矿车翻倒，伴有混凝土开裂的阵阵响声，3 h后巷道内绞车和带式输送机几乎接触顶板，最大底鼓量达2.7 m。

反底拱破坏主要原因是自回风大巷174.3 m处，巷道完全进入断层破碎带，作用于支护体上的围岩压力增大，超过了支护体极限承载能力；支护体储备承载力不足，需要进一步提高支护体整体承载能力，对反底拱进行结构优化设计。

3　钢管混凝土支架底拱段结构力学分析

喷射混凝土与钢管混凝土支架支护体成型后，一旦围岩产生较大变形，喷射混凝土破坏，支护体整体承载能力削弱。考虑支护体整体承载能力条件下，钢管混凝土支架与喷射混凝土同样仅允许发生小变形。为了方便计算认为钢管混凝土支架发生的变形为弹性变形。

原有支护方案中钢管混凝土支架形状为浅底拱圆形。较浅的底拱可减少巷道底板开挖量。但底拱段钢管混凝土支架矢跨过小会导致反底拱内力增大。

3.1力学模型建立

巷道顶底板中极软岩厚度达42 m，且含水状态接近饱和，围岩强度极低，可手捏成团，呈现塑性流动状态。因此，巷道围岩压力可简化为静水压力。

钢管混凝土支架的底拱段与两帮段成一定角度相交，采用底脚套管连接，底脚套管的结构如图3所示。

图3　底脚套管结构

底脚套管经过加强设计，可有效限定支架各节端部的转动与沿钢管轴向的位移，底脚套管对反底拱的约束可视为固支约束。

受均布静水压力作用的钢管混凝土支架反底拱段简化后的力学模型如图4。钢管混凝土支架荷载为均布水压p，钢管混凝土反底拱为固支约束，底拱半径为R，根据几何关系跨度可表示为:

图4　反底拱内力计算力学模型

式中:D——底拱跨度；

R——反底拱半径；

φ——反底拱所对圆心角弧度值的一半，rad。

3.2结构力学求解

反底拱内力求解问题转化成等截面圆弧形无铰拱均布水压作用下的内力，这种状态下，反底拱的承载能力受控于反底拱矢跨比（底拱深度与跨度之比）。底拱跨度一定时，矢跨比仅与底拱深度相关。

为方便理论计算，将矢跨比转化为关于反底拱所对圆心角弧度值的一半的表达式。根据图4中的几何关系，矢跨比与反底拱所对圆心角弧度值的一半之间具有如下对应关系:

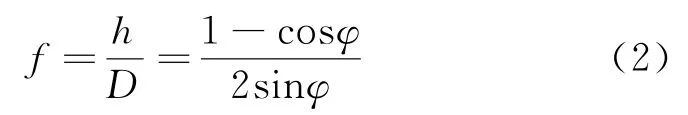
式中:h——底拱深度；

f——矢跨比。

假设支架正常工作条件下处于弹性阶段，则无铰拱的求解为弹性条件下3次超静问题，利用弹性中心法进行求解。将受力状态分3步求解:不考虑轴向变形的无铰拱内力；无铰拱轴向变形造成的拱内附加力；合并前两者，求得无铰拱内力。

（1）忽略轴向变形，基本结构在荷载作用下的受力状态非常简单:

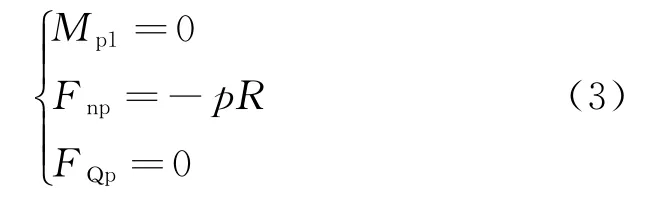
式中:Mp1——忽略变形条件下，无铰拱弯矩；

FQp——忽略变形条件下，无铰拱剪力；

Fnp——忽略变形条件下，无铰拱轴力。

（2）在考虑圆弧拱轴向变形，利用结构的对称性，将无铰拱由跨中位置截开，并加一对刚臂，引入作用于无铰拱弹性中心的附加力，即弯矩、压力和剪力（由于对称，剪力为0）。

弹性中心与圆弧拱的圆心距离为:

式中:d——弹性中心与圆弧拱的圆心距。

力法基本方程和力法方程中系数和自由项计算方程为:

式中:X1——弹性中心附加弯矩；

X2——弹性中心附加压力；

X3——弹性中心附加剪力；

p——作用于圆弧拱上的均布水压力；

E——反底拱的弹性模量；

A——反底拱截面积；

I——反底拱的抗弯刚度；

Δ1p——基本结构所受外因造成的沿X1方向的广义荷载位移；

Δ2p——基本结构所受外因造成的沿X2方向的广义荷载位移；

δ11——X1的位移系数；

δ22——X2的位移系数。

根据式（5）与式（6），可求解附加力X1和X2。

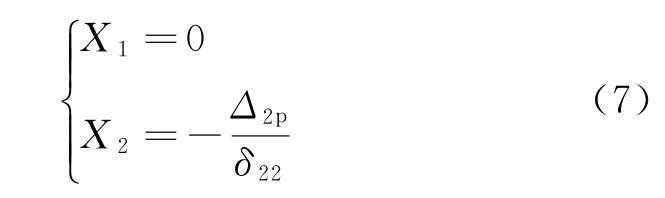
（3）合并无铰拱无轴向变形条件下的内力与轴向变形所引起的附加内力，可得:

式中:Mp——待求点弯矩；

Fn——待求点轴力；

φ0——反底拱上内力待求点和O连线与y轴所成角度。

由式（8）可知，最大轴力在跨中处，最大弯矩在拱脚处或拱顶处。根据式（8）求拱脚（φ0=φ）弯矩与跨中（φ0=0）弯矩之比为:

式中:α——拱脚弯矩与跨中弯矩之比。

圆弧拱所对圆心角的一半取值范围为（0，π/2），拱脚弯矩与跨中弯矩之比随圆弧拱所对圆心角变化情况如图5。由曲线可知，拱脚弯矩始终大于跨中弯矩。

图5　拱脚弯矩与跨中弯矩之比随圆弧拱所对圆心角变化情况

一般认为巷道宽度是一定的，即底拱跨度为已知。弹性中心与圆弧拱的圆心距、底拱曲率半径都可以用底拱跨度表示，且都是关于φ的函数。由式（4）和图4几何关系可得:

式中:EI——圆弧拱的抗弯刚度；

EA——圆弧拱的抗压刚度。

式（11）中，圆弧拱抗弯刚度与抗压刚度与材料有关，材料一旦确定即为定值。因此，当反底拱受到一定均布荷载作用时，拱内最大弯矩和轴力出现在拱顶或拱脚处（即φ0=0或φ0=φ时）。拱内最大弯矩和轴力仅受控于变量φ，而矢跨比与φ具有一一对应的关系。因此，拱内最大弯矩和轴力仅与矢跨比有关。

3.3不同矢跨比钢管混凝土支架反底拱内力分析

在巷道支护中，巷道围岩变形稳定前，支护体支护阻力与作用在支护体上的荷载是一个动态变化的相互作用过程。巷道围岩地质条件复杂，支护体工作状态中，作用于支护体上的荷载是难以准确评估的。

回风大巷围岩为极软岩，且接近饱水状态，可认为作用于支护体上的荷载为均布荷载。但荷载大小不能确定，由式（11）可看出，无铰拱内弯矩与轴力都与荷载成正比，因此，为方便反底拱内力分析，可赋予荷载一假定值，进行定量化分析，考察在无铰拱某一均布荷载作用下，拱内轴力和弯矩随矢跨比的变化情况。

假设作用于支护体上的荷载为均布荷载，其中有0.6 MPa由支架承担，支架间距为0.7 m，可认为每架钢管混凝土支架承担的线荷载q为420 k N/m。

根据《钢管混凝土拱桥技术规范:GB 50923 -2013》，钢管混凝土抗压刚度和抗弯刚度为:

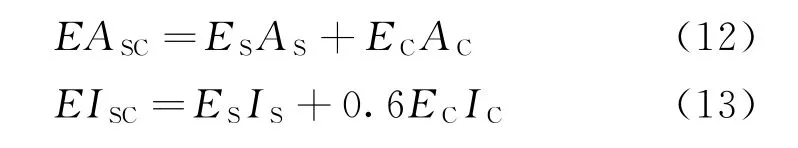
式中:EASC——钢管混凝土的抗压刚度；

联立式（6）、（7）、（8）和（10）可得弯矩和轴力表达式:

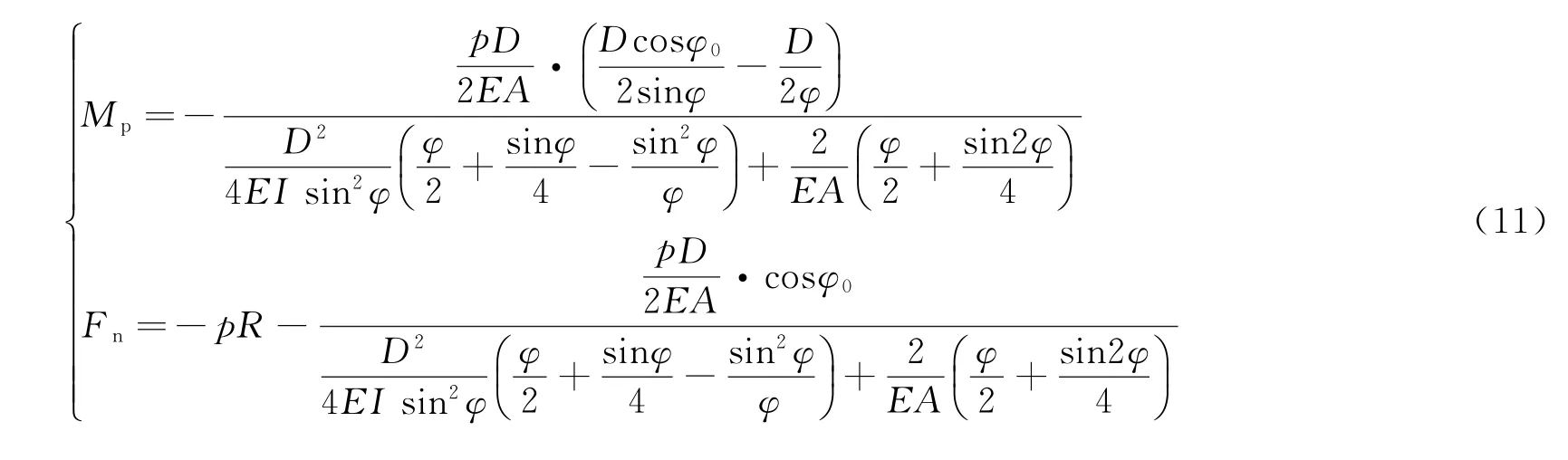
EISC——钢管混凝土的抗弯刚度；

ES——钢材的弹性模量；

EC——混凝土的弹性模量；

AS——钢管的横截面积；

AC——钢管内混凝土的横截面积；

IS——钢管对其重心的惯性矩；

IC——钢管内混凝土对其重心的惯性矩。

以钢管型号ø194 mm×10 mm的钢管混凝土结构为例，根据 《钢管混凝土拱桥技术规范:GB 50923-2013》，ES取2.06×105N/mm2，EC取3.25×104N/mm2，钢管横截面积A s取5780 mm2，钢管内填混凝土横截面积A c取23778 mm2，当底拱跨度和均布荷载一定时，钢管的惯性矩为24523023 mm4，混凝土的惯性矩为44972462 mm4。代入式（12）和式（13），计算得EASC为1.96×109N，EISC为5.92×106N·m2。

支架底拱跨度为5.8 m，将EASC、EISC、q及数据代入式（11），求出拱内轴力和拱内弯矩随φ变化关系。计算得出，拱内轴力、拱内弯矩、反底拱所对圆心角弧度值的一半和矢跨比的对应关系如表2所示，跨中轴力与拱脚弯矩随矢跨比变化情况如图6所示。

由图6可知，跨度为5.8 m的ø194 mm× 10 mm钢管混凝土支架反底拱段，随着矢跨比的减小，拱内最大轴力和弯矩增大。由表2可知:当矢跨比小于0.25时，拱内最大轴力随矢跨比的减小明显增大。矢跨比为0.15、0.2和0.25的圆弧拱拱内最大轴力分别是矢跨比为0.3圆弧拱拱内最大轴力的1.65倍、1.29倍和1.1倍；矢跨比为0.15、0.2和0.25的圆弧拱拱内最大弯矩值分别是矢跨比为0.3圆弧拱拱内最大弯矩值的3.55倍、2.08倍和1.36倍。

图6　拱内跨中轴力和拱脚弯矩随矢跨比变化情况

表2　不同矢跨比条件下圆弧拱内力情况

考虑到矢跨比越大卧底量越大，钢管弧长也越长。建议极软岩巷道中使用的钢管混凝土支架圆弧拱矢跨比取值范围为0.25～0.3。原支护方案中使用的钢管混凝土支架反底拱深度0.9 m左右，反底拱宽度5.8 m，矢跨比约为0.15，有待进一步优化设计。

4　支护方案设计优化与支护效果

4.1支架结构优化

对钢管混凝土支架进行结构设计优化，优化设计后支护方案中钢管混凝土支架反底拱矢跨比为0.25。反底拱宽度由5.7 m改为5.5 m，拱的深度由0.94 m改为1.37 m。假设现有支护方案中支架受力状态与原有支护方案中一致，根据式（9）进行理论计算。优化后钢管混凝土支架反底拱拱内最大轴力为1475 k N，是原有方案中反底拱拱内最大轴力的65%；其最大弯矩为24.8 k N·m，为原有反底拱的46%。据此，可认为优化后钢管混凝土支架承载能力可达原有支架承载能力的1.53倍（1/0.65=1.53）。能够维持巷道围岩稳定。巷道支护断面如图7所示。

图7　巷道支护断面图

4.2支护效果

自2012年9月至今，查干淖尔一号井回风大巷使用钢管混凝土支架返修完工已经有2年时间。表观上，混凝土喷层未发生明显变形。

5　结论

（1）根据工程实践中，钢管混凝土支架反底拱的受力情况与约束情况，建立了小变形条件下计算钢管混凝土支架内力的力学模型，经理论分析发现:在均布荷载作用下，跨度一定的反底拱拱内弯矩与轴力随着矢跨比的减小而增大，特别是当矢跨比小于0.25时，拱内弯矩与轴力急剧增大。根据理论分析结果，建议极软岩巷道中使用的钢管混凝土支架反底拱矢跨比为0.25～0.3。

（2）设计了查干淖尔一号井回风大巷返修方案，将原有支护中支架底拱段的矢跨比由0.15增大至0.25，支架钢管型号依然采用ø194 mm× 10 mm。巷道支护完成2年后，巷道稳定，无明显变形。

［1］ 高延法，王军，黄万朋.直墙半圆拱形钢管混凝土支架力学性能实验及应用 ［J］.隧道建设，2014（1）

［2］ 刘珂铭，高延法，郭贺等.深井软岩巷道钢管混凝土支架复合支护技术［J］.中国煤炭，2015（6）

［3］ 高延法，冯绍伟，刘珂铭等.极软岩返修巷道钢管混凝土支架支护方案研究 ［J］.中国煤炭，2014（11）［4］ 张晓凤，颜伟.钢管混凝土支架在华丰煤矿深井支护中的应用［J］.煤矿机械，2011（7）

［5］ 彭可平，董智慧.煤层冲刷带软岩巷道支护技术研究［J］.中国资源综合利用，2011（7）

［6］ 李学彬，杨仁树，高延法等.大断面软岩斜井高强度钢管混凝土支架支护技术［J］.煤炭学报，2013（10）

［7］ 王军，陈锋，刘国磊等.千米深井巷道钢管混凝土支架支护技术应用［J］.隧道建设，2013（9）

［8］ 高延法，王波，曲广龙等.钢管混凝土支架力学性能实验及其在巷道支护中的应用 ［A］.第八届海峡两岸隧道与地下工程学术与技术研讨会 ［C］.台湾，2009

［9］ 曲广龙.钢管混凝土支架结构抗弯性能研究及应用［D］.中国矿业大学（北京），2013

［10］ 黄万朋.深井巷道非对称变形机理与围岩流变及扰动变形控制研究 ［D］.中国矿业大学（北京），2012

［11］ 高延法，王波，王军等.深井软岩巷道钢管混凝土支护结构性能试验及应用 ［J］.岩石力学与工程学报，2010（S1）

Optimization design of the structure of concrete-filled steel tube supports in the extremely soft rock roadway

He Xiaosheng1，Yu Guanglong2，Sun Xiaotong1，Yang Yongqian2
（1.School of Mechanics and Civil Engineering，China University of Mining and Technology，Beijing，Haidian，Beijing 100083，China；2.Jizhong Energy Resources Co.，Ltd.，Handan，Hebei 056107，China）

Aiming to solve the buckling failure problem of inverted arch of concrete-filled steel tube supports in main return way of Chagannaoer No.1 Coal Mine，the reason for deformation and fracture was analyzed.When the clamped restraint of arch springer was affected by even load，the laws that the internal force of circular arch changed with the rise-span ratio were researched using structural mechanics analysis method.The theoretical calculation results showed that when the supports was under a certain even load and the rise-span ratio of circular arch was less than 0.25，the maximum axial force and the maximum bending moment in the inverted arch ofø194 mm×10 mm type concrete-filled steel tube supports decreased obviously with the increasing of rise-span ratio，and the reasonable rise-span ratio was 0.25～0.3.The concrete-filled steel tube supports whose rise-span ratio was 0.25 were adopted instead of the former supports，while keeping other supporting scheme unchanged.Practice has proven that there was no obvious deformation since the roadway completed repair 2 years ago.

extremely soft rock roadway，concrete-filled steel tube support，structural design，rise-span ratio

TD353

A

何晓升（1989-），男，山东菏泽人，博士研究生，主要从事软岩巷道支护与支护结构设计研究工作。

（责任编辑 张毅玲）

国家自然科学基金面上资助项目（51474218），国家自然科学基金重点项目（51134025）