地面大功率干扰源对导航星座星间链路的干扰分析

王东会，徐博，刘文祥，孙广富



地面大功率干扰源对导航星座星间链路的干扰分析

王东会，徐博，刘文祥，孙广富

(国防科学技术大学电子科学与工程学院卫星导航研发中心，湖南长沙，410073)

为了定量分析地面大功率干扰源对导航星座星间链路的影响程度，提出单星干扰解析模型，通过等效载噪比定量描述干扰强度，通过测距误差和通信误码率衡量干扰对单颗导航卫星的影响。根据导航星间链路的工作特点，对卫星受干扰导致整星座星地联合定轨及星间转发通信功能异常的原理进行分析。研究结果表明：星间链路系统具有较强的抗地面干扰的能力，地面单个大功率干扰源对星地联合定轨精度的影响小于厘米级，对星间转发通信的影响仅为部分卫星的链路传输代价增加以及直接干扰卫星一段时间内的通信异常。

星间链路；地面大功率干扰；星地联合定轨；星间转发通信；等效载噪比

星间链路是卫星导航系统的重要组成部分。GPS Block IIR以及Block IIF卫星已采用UHF频段建立星间链路，采用TDMA体制协调整星座的测距和通信时序[1]。整个星座可以脱离地面站的支持而独立地运行180 d，大大提高了星座战时生存能力[2−3]。到GPSIII阶段，星间链路可能采用a(频率为23 GHz)或(频率为60 GHz)频段，星间链路天线实现点波束，可提高通信速率和抗干扰能力[4]。GLONASS，GALILEO以及BDS系统对星间链路的建设也处于研究和论证阶段[5−6]。对于地面监测站分布在局部地区的卫星导航系统，星间链路尤为重要。这不仅表现为战时的星座自主运行，更重要的是在平时，星间链路可以为无法直接上注的境外卫星转发通信信息，从而维持整个星座对全球用户的导航服务能力。在未来导航战背景下，卫星导航星间链路可能受到各种人为或意外干扰，严重时甚至影响整个导航系统的正常运行。有必要对这种影响效果进行分析，并在此基础上增加抗干扰措施。目前在通信卫星网络的可靠性及抗毁性分析评估方面已有一些研究成果，如文献[7]提出一种快速分析评价通信网可靠性的方法等。在卫星导航抗干扰性能分析方面也已有较多研究成果，如文献[8]提出以平均信噪比损耗为指标评估空域抗干扰的性能；文献[9]对天线阵抗干扰评估方法进行了分析。但这些分析方法均是针对地面导航接收终端，不能完全适用于星间链路系统，需要根据导航星间链路的特点有针对性地研究适合的干扰影响分析方法。本文作者在上述研究成果的基础上，针对导航星间链路的特点，提出单星干扰解析模型，进而对星地联合定轨及星间转发通信受干扰的原理进行分析，最后以典型的Walker24/3/2星座以及a点波束天线星间链路为例进行仿真实验，对基于地面单个大功率干扰源的干扰影响进行分析。

1 单星干扰解析模型

地面大功率干扰信号经过空间传播，经由星间链路天线进入卫星。卫星受影响程度由进入卫星天线口面的干扰信号强度决定。由于卫星始终处于运动状态，卫星与地面干扰源的相对位置关系是时变的，导致干扰信号影响也是时变的。为了分析方便，本文提出单星干扰解析模型，给出任意时刻地面干扰源对卫星的干扰强度计算方法。

地面对卫星干扰示意图如图1所示。其中：为地心；S为某颗导航卫星；为地面干扰源；矢量方向为天线方向图中心指向。

图1 地面大功率干扰源对单颗卫星的干扰示意图

地面干扰信号相对卫星的来向定义为：惯性系下干扰信号与卫星地心间连线的夹角，即∠JSO。从图1可以看出：干扰信号相对卫星的来向与干扰源对卫星的观测方向相反。假设卫星S的位置矢量为()，干扰源位置矢量为()，则干扰来向可通过余弦定理得到：

(1)

假设星间链路天线方向图俯仰方向的中心为图1中的方向，则对于不同的星间天线形式，方向是不同的，有如下2种情况。

1) 对于宽波束天线，如GPSIIR的UHF天线，星间天线指向不变，假设星间链路天线仰角范围为[min,max]，则天线方向图中心指向可表示为

2) 对于点波束天线，如GPSIII可能采用的a或频段点波束天线，卫星间通过波束扫描的方式实现相互对准，因此，波束指向是随时间变化的，可表示如下：

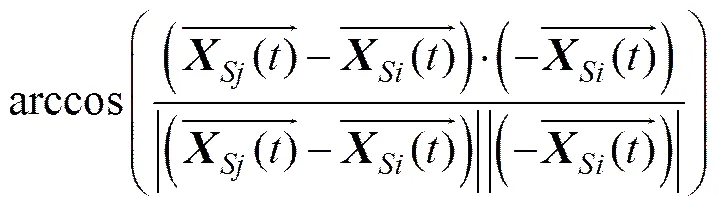
其中：S为与S天线对准的卫星。于是，可以得到干扰方向与卫星方向图中心的夹角为

(4)

∠ASJ随时间变化，根据天线方向图即可得到星间天线对干扰信号的增益。根据信号空间传播定理，可得到任意时刻卫星接收到的干扰信号强度为

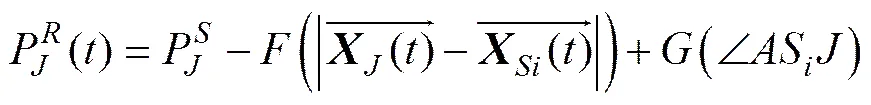
其中：P为地面干扰源天线出口功率；为空间传播损耗函数，损耗功率由干扰源与卫星间的距离决定；为星间链路天线方向性增益函数。

本文采用等效载噪比描述干扰信号程度。扩频通信体制的等效载噪比计算方法如下[10]：

其中：()为无干扰时的信号接收载噪比；P()为星间链路正常信号接收功率；是为各种类型干扰源和调制器而确定的抗干扰品质因数；C为扩频码码速率。

地面干扰源对单颗卫星的影响主要从测距误差以及通信误码率两方面来衡量，具体方法如下。

1) 干扰对测距误差的影响。根据等效载噪比以及典型的码跟踪环测量误差原理[11]可得到存在干扰时的测距误差jam()，进而可得到卫星S对卫星S的测距为

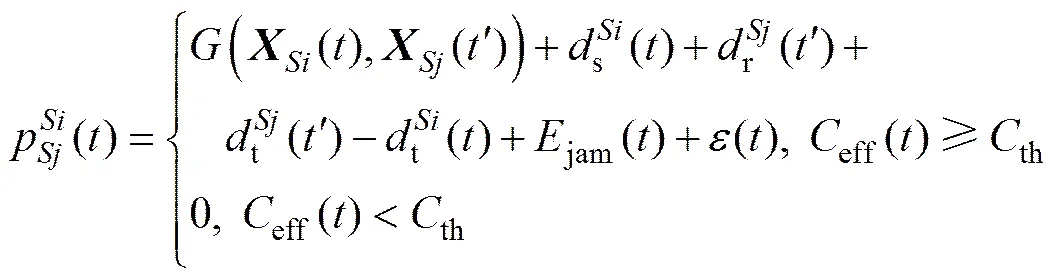
其中：为距离观测函数；为信号发射时刻；为信号接收时刻；()为卫星位置矢量；s()为发射零值；r()为接收零值；t()为钟差；()为随机误差；jam()为干扰引入的测距误差；eff为等效载噪比；th为接收载噪比门限。

式(7)的含义是：当等效载噪比超过接收机载噪比门限时，测距误差增大；当等效载噪比低于载噪比门限时，接收机无法测距。

2) 干扰对通信误码率的影响：首先将等效载噪比换算为等效信噪比，分贝形式的换算方法如下：

根据BPSK信号信噪比与误码率的关系确定干扰对通信误码率的影响[10]：

其中：erfc( )为互补误差函数。

当误码率超过系统可容忍的门限eth时，该卫星的通信将不可用。

2 整星座干扰影响原理

当存在干扰时，可通过单星干扰解析模型得到单星测距误差和误码率影响。但一个网络中的某个节点受干扰时，其影响往往不局限于单个节点，而可能因为节点重要性不同对整个网络产生不同程度的影响。这里根据导航星间链路工作体制的特点论述地面大功率干扰源对整个星间链路系统的干扰影响原理。

2.1 导航星间链路工作原理

星间测距和星间通信是导航星间链路系统的两大主要功能，通过星间测距及通信可完成星座自主导航、星地联合定轨以及上注星历等信息的传输。

导航星座星间链路工作原理示意图如图2所示。

图2 星间链路工作原理示意图

星间链路系统通常按照星座运行周期划分为若干个工作周期以及工作时隙[2]，对星座所有卫星进行合理的测距规划，在1个工作周期内获得尽可能多的星间测距信息。这些测距信息通过星地链路下传到地面主控中心。主控中心结合星间测距及各地面监测站对卫星的测距信息进行精密定轨解算。对精密定轨结果进行轨道外推得到各卫星的广播星历，通过上行链路将广播星历注入给各导航卫星。注入站可视卫星直接注入，不可视卫星通过星间链路进行信息转发通信。

从上述分析可以得出：当卫星受到干扰时，整星座精密定轨及星间转发通信都可能受到影响。

2.2 干扰对整星座精密定轨的影响

等效载噪比高于载噪比门限时，对式(7)在卫星初始状态0处进行泰勒展开，得到线性化方程：

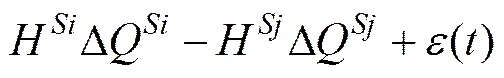
参照式(7)和(10)可得到类似的星地线性化观测方程，将星间和星地测距方程组成联合解算方程如下：

(11)

其中：Y()为星地观测残差；Y()为星间观测残差；为观测矩阵；Δ为待估参数，包含卫星三维位置、速度、钟差以及日月引力、地球非球形引力、太阳光压等摄动力参数[11]。

对式(11)进行最小二乘估计即可得到基于星地、星间测距的联合定轨结果。

由最小二乘估计原理可知：受干扰影响的星间测距数量越多，测距误差越大，则联合定轨结果精度越低。由于联合定轨对所有卫星同时解算，因此，整星座所有卫星的定轨结果都将包含干扰影响。

2.3 干扰对转发通信的影响

地面站与不可视卫星通信时，首先要选择1个地面接触卫星节点，即选择1个最佳的地面站直接可视卫星。将通信信息首先传输给该卫星，然后进行星间网络的最优路由计算，选择最优路径将信息由接触点卫星传递给目标卫星，完成转发通信。

导航星间链路通常采用基于最小代价的K短路径算法进行最优路由计算[12]，代价可以根据系统需求选择传输时延和链路切换次数等。

地面干扰源对星间链路通信的干扰可以分为2个方面：一是对星地传输链路进行干扰，即干扰地面接触卫星节点的上注信号接收；二是对星间传输链路进行干扰。星地链路受干扰对整个卫星导航系统将产生很大影响，卫星无法获得上注广播星历，从而无法为用户提供导航服务。在通常情况下，星地链路与星间链路采用不同的工作频段，对星间链路进行干扰的干扰源无法同时对星地链路进行干扰，加之上注链路本身具有很高的抗干扰性能，因此，本文仅就星间传输链路受干扰的情况进行分析。

干扰对星间转发通信的影响表现为2点：

1) 直接被干扰卫星通信异常，影响程度由信号接收误码率和误码率门限确定。卫星重新进入地面注入站可视范围内时，可恢复正常通信。

2) 当2颗卫星间的最优传输路径上的某个节点卫星因干扰而误码率提高甚至不可通信时，需要剔除该卫星并重新计算星间路由。新得到的传输路径整体代价大于原最优路由的代价。

因此，干扰对星间转发通信的影响就表现为部分卫星传输链路代价增加以及直接干扰卫星一段时间内通信出现异常。受干扰的卫星数量越多，受干扰卫星在整网中作为中转节点的次数越多，则整网通信代价增加越大。

3 算例分析

3.1 仿真条件

3.1.1 星座条件

未来的卫星导航系统将普遍采用3个轨道面的星座结构[13]。因此，本文仿真时选用3个轨道面的Walker星座。利用美国AGI公司的STK软件创建星座场景。仿真时间为2008−07−02T12:00—2008−07−03T12:00，仿真时间间隔5 min。星座相关参数如下[6]：

1) 星座构型为Walker24/3/2；

2) 轨道半长轴为24 126 km；

3) 轨道倾角为55°；

4) 星间天线采用4个a点波束天线。天线波束主瓣宽度为10°，旁瓣抑制超过30 dB。

3.1.2 建链方式

星间建链方法为：每颗卫星同时建立4条链路，星间测距时刻根据可见卫星情况动态分配测距链路，保证所有可见卫星在1个星间链路周期内至少建立1次链路；星间通信时刻在所有可见卫星中按照最优路径建链。

3.1.3 干扰源参数

由于星间链路窄波束天线具有较好的旁瓣抑制作用，要想对星间链路实施有效干扰，地面干扰源需具备较大的发射功率。因此，地面干扰源需采用窄波束天线，使干扰信号能量集中，每个干扰源只能针对1颗卫星实施定向干扰。

根据当前a频段功放及大口径天线技术水平[14−15]，地面大功率干扰源参数设置如表1所示。

表1 干扰源参数

3.1.4 仿真场景

选择第1颗卫星MEO11作为地面接触点卫星，选择第19颗卫星MEO33作为被干扰卫星。由于Walker星座具有良好的对称性和周期性，因此，选择上述卫星进行仿真可代表整个星座的特性。假设地面设立单个干扰源，干扰源位置为(77 ºW，39 ºN)，固定对MEO33卫星进行干扰。

3.2 仿真结果

3.2.1 等效载噪比仿真结果

按照单星干扰解析模型，当卫星MEO33受到地面大功率干扰时，其接收同轨道相邻卫星MEO32和异轨道卫星MEO23信号时，等效载噪比与正常无干扰条件下的载噪比对比结果如图3所示。

由于MEO33与MEO32卫星是同轨道相邻卫星，相对位置关系不随时间变化，因此，图3(a)中无干扰条件下的载噪比保持不变。由于地面干扰源相对卫星MEO33的位置关系不断变化，因此，等效载噪比存在一定幅度的上下波动。图3(b)中载噪比为0的时段表示MEO33和MEO23卫星不可视。载噪比的波动原因为异轨道卫星相对位置关系随时间变化。

由图3可知：等效载噪比均低于20 dB∙Hz，此结果远低于正常接收机信号捕获门限，因此，干扰时间段内MEO33卫星无法接收测距和通信信号。

(a) MEO33接收MEO32卫星信号；(b) MEO33接收MEO23卫星信号

3.2.2 星地联合定轨仿真结果

利用星间链路测距数据和星地下行测距数据按照式(11)对整星座24颗卫星进行联合定轨解算。无干扰条件下和卫星MEO33受干扰条件下的星座平均定轨结果如表2所示。

表2 联合定轨仿真结果

由表2可知：当单个卫星MEO33受干扰时，对整星座定轨结果的影响在厘米级以下。这是因为星间链路中每颗卫星可扫描到的卫星个数均有12~16颗[16−17]，单个卫星受干扰仅导致1个测距链路受损失，卫星间仍然有足够的可用测距数量。

要想对卫星定轨产生较大的影响，必须增加地面干扰源数量，对更多的卫星实施干扰。

3.2.3 星间转发通信仿真结果

为了分析方便，本文选择路径传输时延作为整网通信代价。按照K短路径算法选择传输时延最小的路径作为最优通信路径。假设某时刻从地面接触节点卫星MEO11向整网其他卫星发起通信传输业务。正常无干扰条件下与MEO33受干扰条件下各卫星数据传输时延如图4所示。

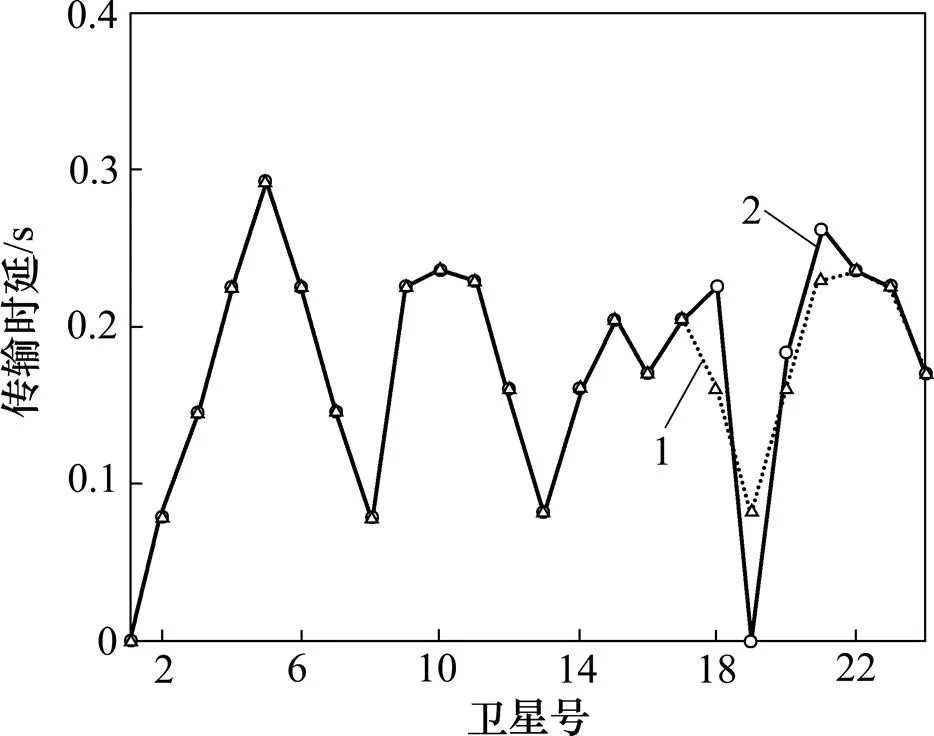
1—无干扰；2—MEO33受干扰

对于Walker星座来说，从任意一颗卫星节点到整网其他卫星最多仅需要1次中转，即星间链路的通信最多经过3颗卫星。从MEO11到整网其他卫星的最优链路中，第19号卫星MEO33作为中转卫星出现了3次，因此，当MEO33受干扰时，这3条路径需要重新计算。从图4可见：重新计算的3条链路分别为MEO11到第18号卫星MEO32、第20号卫星MEO34以及第21号卫星MEO35。这3条路径的链路传输时延增加量分别为0.063 9，0.021 1和0.033 1 s。而MEO33卫星由于干扰而无法接收通信信号。

4 结论

1) 针对地面大功率干扰源对星间链路的干扰影响问题进行了分析，提出了单星干扰解析模型，并根据星间链路特点分别论述了干扰对整网精密定轨及星间转发通信的影响原理。

2) 当星间链路采用点波束天线时，对地面干扰信号具有较好的抑制作用，但由于地面干扰源发射功率可以很高，因此，存在干扰时的等效载噪比仍然比正常条件下降低了20 dB以上，被干扰卫星无法接收测距和通信信号。

3) 地面单个干扰源对整星座平均定轨精度的影响小于厘米级。以被干扰卫星作为中转节点的通信链路均需要重新计算路由，新路径代价必然高于原最优路径的代价。单个链路传输时延最多增加63.9 ms。直接被干扰卫星在进入地面站可视范围前将无法接收转发通信信息。

4) 虽然地面干扰源可对星间链路产生一定影响，但只有当干扰源数量足够多以致大部分卫星无法工作时，才可能对整星座产生较大影响。

参考文献：

[1] Fisher S C, Ghassemi K. GPS IIF-the next generation[J]. Proceedings of the IEEE, 1999, 87(1): 24−47.

[2] Rajan J A. Highlights of GPS II-R autonomous navigation[C]// Proceedings of the 58th Annual Meeting of the Institute of Navigation and CIGTF 21st Guidance Test Symposium. Albuquerque: ION, 2002: 354−363.

[3] Fernandez F A. Inter-satellite ranging and inter-satellite communication links for enhancing GNSS satellite broadcast navigation data[J]. Advances in Space Research, 2011, 47(5): 786−801.

[4] Maine K, Anderson P, Bayuk F. Communication architecture for GPSIII[C]// Proceedings of The IEEE Aerospace Conference. Los Angeles: IEEE Press, 2004: 124−129.

[5] Sanchez M, Pulido J A, Amarillo F, et al. The ESA “GNSS+” project inter-satellite ranging and communication links in the frame of the GNSS infrastructure evolutions[C]// Proceedings of the 21stInternational Technical Meeting of the Satellite Division of the Institute of Navigation. Savannah: ION, 2008: 2538−2546.

[6] 徐勇, 常青, 于志坚. GNSS星间链路测量与通信新方法研究[J]. 中国科学: 技术科学, 2012, 42(2): 230−240. XU Yong, CHANG Qing, YU Zhijian. One new measurement and communication techniques of GNSS inter-satellite links[J]. Scientia Sinica: Technologica, 2012, 42(2): 230−240.

[7] 郭伟. 野战地域通信网可靠性的评价方法[J]. 电子学报, 2000, 28(1): 3−6. GUO Wei. Reliability evaluation method of tactical communication network[J]. Acta Electronic Sinica, 2000, 28(1): 3−6.

[8] Fante R L, Vaccaro J J. Evaluation of adaptive space-time- polarization cancellation of broadband interference[C]// Proceedings of the IEEE Position Location and Navigation Symposium. California: IEEE Press, 2002: 1−3.

[9] 聂俊伟, 葛锐, 李垣陵, 等. 基于导航定位服务性能的GNSS天线阵抗干扰统计性能评估方法[J]. 国防科技大学学报, 2012, 34(2): 81−87.NIE Junwei, GE Rui, LI Yuanling, et al. Performance evaluation method for GNSS anti-jam antenna arrays based on the navigation service performance[J]. Journal of National University of Defense Technology, 2012, 34(2): 81−87.

[10] Kaplan E D. GPS原理与应用[M]. 寇艳红, 译. 北京: 电子工业出版社, 2006: 181−200. Kaplan E D. Understanding GPS principles and applications[M]. KOU Yanhong, trans. Beijing: Publishing House of Electronics Industry, 2006: 181−200.

[11] ZHOU Shanshi, HU Xiaogong, WU Bin. Orbit determination and prediction accuracy analysis for a regional tracking network[J]. Sci Sin Phys Meth Astron, 2010, 53(6): 1130−1138.

[12] 周建华, 杨龙, 徐波, 等. 考虑波束限制的改进导航星座星间链路方案[J]. 中国科学: 物理学力学天文学, 2011, 41(5): 575−580. ZHOU Jianhua, YANG Long, XU Bo, at el. An improved satellite link scheme with beam restriction for the navigation constellation[J]. Scientia Sinica: Physica, Mechanica & Astronomica, 2011, 41(5): 578−580.

[13] 谭述森. 北斗卫星导航系统的发展与思考[J]. 宇航学报, 2008, 29(2): 391−396. TAN Shusen. Development and thought of compass navigation satellite system[J]. Journal of Astronautics, 2008, 29(2): 391−396.

[14] Ben M R, Einat M. 23 GHz ferroelectric electron gun based gyrotron[J]. Applied Physics Letters, 2011, 98(17): 173506− 173509.

[15] Rzesnicki T, Piosczyk B, Kern S, et al. 2.2-MW record power of the 170-GHz European preprototype coaxial-cavity gyrotron for ITER[J]. IEEE Transactions on Plasma Science, 2010, 38(6): 1141−1149.

[16] ZHOU Shanshi, HU Xiaogong, WU Bin. Orbit determination and time synchronization for a GEO/IGSO satellite navigation constellation with regional tracking network[J]. Sci Sin Phys Meth Astron, 2011, 54(6): 1089−1097.

[17] 周善石. 基于区域监测网的卫星导航系统精密定轨方法研究[D]. 北京: 中国科学院研究生院, 2011: 78−90. ZHOU Shanshi. Studies on precise orbit determination theory and application for satellite navigation system with regional tracking network[D]. Beijing: Graduate School of Chinese Academy of Science, 2011: 78−90.

[18] WANG Donghui, NI Shaojie, LIU Wenxiang, et al. Compass satellite orbit determination based on inter-satellite and satellite- to-station ranging[C]// The 25th International Technical Meeting of the Satellite Division of the Institute of Navigation. Nashville TN, 2012: 340−346.

Jamming effects analysis of ground power jamming source on navigation inter-satellite links

WANG Donghui, XU Bo, LIU Wenxiang, SUN Guangfu

(Satellite Navigation Research and Development Center, National University of Defense Technology, Changsha 410073, China)

In order to quantitatively analyze the jamming effects of ground power jamming source on navigation inter-satellite links (ISL), an analytical model for single satellite jamming was proposed. The model describes jamming signal strength by equivalent carrier to noise ratio (CNR), and describes jamming effects on single satellite by ranging error and communication bit error rate (BER). Jamming principle on satellite orbit determination and inter-satellite communication of the whole constellation was analyzed according to ISL operating mode. The results show that ISL has a good anti-jamming performance. Satellites orbit error caused by single ground power jamming source is less than centimeter level. Transmission delay of some satellites increases because of the jamming, and the directly jammed satellite can not communicate for a period of time.

navigation inter-satellite links; ground power jamming source; orbit determination; inter-satellite communication, equivalent CNR

10.11817/j.issn.1672-7207.2015.07.019

TN967.1

A

1672−7207(2015)07−2517−07

2014−07−13；

2014−10−19

教育部新世纪优秀人才支持计划项目(NCET-08-0144) (Project((NCET-08-0144) supported by Program for New Century Excellent Talents in University)

王东会，博士研究生，从事卫星导航应用研究；E-mail: wdhhawk@163.com

(编辑 杨幼平)