基于碟形砂轮磨齿的面齿轮齿面主动设计方法
郭辉,项云飞,赵宁
基于碟形砂轮磨齿的面齿轮齿面主动设计方法
郭辉,项云飞,赵宁
(西北工业大学机电学院,陕西西安,710072)
基于局部综合法、双层优化法以及碟形砂轮展成磨削原理,提出面齿轮齿面的主动设计方法。通过砂轮齿廓修形参数的优化获得预设幅值和形状对称的传动误差函数;通过对砂轮的多轴数控运动控制获得预期的齿向修形模式。研究结果表明:该方法使设计人员能够按照要求的传动性能来设计面齿轮齿面的形状,并可在数控磨齿机上进行加工;齿面主动设计能保证面齿轮副的传动误差和接触路径满足预先设计的要求。
面齿轮;主动设计;碟形砂轮;磨齿;接触印痕;传动误差
面齿轮传动具有结构紧凑、安装调整方便、传动比大的优点[1]。据报道,已应用于直升机的主传动系统与弧齿锥齿轮相比,能显著降低分扭传动系统的重力并提高承载能力。在面齿轮传动的设计与加工方面,国内外已有不少学者进行相关研究。为了获得传动稳定性并避免边缘接触,Litvin等[2]提出了使用碟形砂轮对直齿面齿轮传动中的小齿轮进行双冠修形的方法,实现预置抛物线传动误差,消除齿顶边缘接触,同时使接触轨迹发生倾斜,增大了重合度,但当有安装误差时会出现不一致的接触椭圆和不均匀接触线移动。Zanzi等[3]研究了通过碟形砂轮对小齿轮进行双冠修形的方法,控制修形因数和磨齿加工运动参数来改变面齿轮接触印痕的位置和方向,并获得抛物线传动误差。Tsay等[4]基于锻造成型技术对面齿轮齿面进行双向修形,该方法可以灵活地控制接触印痕的倾斜角度和重合度以及传动误差幅值,但不适合于齿轮切削加工。采用碟形砂轮[5−6]磨削面齿轮具有结构简单、设计制造方便且不受面齿轮设计参数限制的优点。郭辉 等[7]在5坐标曲面磨床上利用碟形砂轮进行了面齿轮的磨削实验,齿面偏差达到了21 μm以下。Tang等[8]研究了利用碟形砂轮磨削修形面齿轮的原理,扩展了其应用。此外,Wang等[9−10]采用了轮齿承载接触分析的方法来研究面齿轮的啮合特性。吴训成等[11]提出了基于功能需求的齿面主动设计方法,可以直接设计齿面啮合过程中的接触迹线、接触椭圆长轴尺寸及传动的高阶加速度。彭先龙等[12]通过构造圆柱齿轮拓扑修形齿面的方式对面齿轮传动进行了主动设计,预设了接触性能。本文提出点啮合面齿轮的主动设计方法:以传动误差曲线和接触印痕等指标为目标,采用双层优化法和局部接触综合法,通过对5轴联动数控磨齿机加工参数的设计调整,保证加工出的齿面在整个啮合过程中满足预置的传动误差和接触印痕要求,从而实现对齿面啮合质量的全程控制。
1 碟形砂轮磨削面齿轮的原理
1.1 面齿轮磨齿的展成运动
碟形砂轮加工面齿轮的磨齿原理如图1所示。从图1可见:碟形砂轮在2个不同时刻的位置,其中面齿轮与虚拟小齿轮相啮合,虚拟小齿轮与碟形砂轮齿形相配合,因此,碟形砂轮能够与面齿轮正确啮合。为了应用这种加工方法磨削面齿轮,所用碟形砂轮的轴截面齿廓应该与虚拟小齿轮的端面齿廓一致。在磨削面齿轮时,缓慢变化砂轮的安装角并将轴和轴插补,此时砂轮的轴截面齿廓便可看作1个旋转的很薄的小齿轮。与此同时,面齿轮按照传动比规律绕其回转轴作相应的转动,从而模拟了面齿轮与1个很薄的小齿轮之间的啮合,即展成运动。

图1 碟形砂轮的磨齿加工原理图
1.2 磨齿进给运动
由于所用碟形砂轮的轴截面齿廓与虚拟小齿轮的端面齿廓一致,这样在某个加工位置,碟形砂轮与虚拟小齿轮之间形成线接触,而虚拟小齿轮和面齿轮之间也为线接触,此时碟形砂轮与面齿轮之间为点接触,接触点为2条接触线的交点。
为了实现对面齿轮整个齿面的包络,需要面齿轮在2个方向上进行进给。本文作者采取的进给运动为:固定机床的轴角度,让砂轮在虚拟小齿轮轴线方向上(图1所示轴方向)作往复运动,此时砂轮模拟某个时刻处的虚拟小齿轮齿面(若虚拟小齿轮为斜齿轮,在碟形砂轮作平行于机床轴的运动时,砂轮应绕机床轴转动∆,面齿轮也应做相应的补偿转动),碟形砂轮在面齿轮齿宽方向上连续磨削1次,形成面齿轮齿面上的1个带状区域;然后改变砂轮安装角度,再次让砂轮沿面齿轮齿宽方向上连续磨削,则可以形成一系列带状区域,由这些带状区域构成面齿轮的整个齿面。砂轮中心的沿齿宽方向的进给运动,独立于砂轮改变安装角的展成运动。
2 面齿轮的齿面主动设计
采用碟形砂轮展成加工面齿轮,并进行齿面双向修形,以实现对面齿轮齿面接触印痕和传动误差的控制。其中,传递误差由对碟形砂轮的齿廓修整来实现,齿向修形即承载接触的局部化通过控制碟形砂轮中心的运动规律来实现。
2.1 碟形砂轮轴截面齿廓的修形
图2所示为碟形砂轮的轴截面齿廓。碟形砂轮加工面齿轮的工作面是1个旋转曲面,其产形线为轴截面齿廓(如图2中粗实线所示),它与虚拟小齿轮的端面齿廓相同。

图2 碟形砂轮的轴截面齿廓
图3所示为碟形砂轮轴截面齿廓的修形。从图3可见:未修形的碟形砂轮1侧的轴截面齿廓是1条渐开线,记为。在坐标系s中其位矢和法矢可表示为
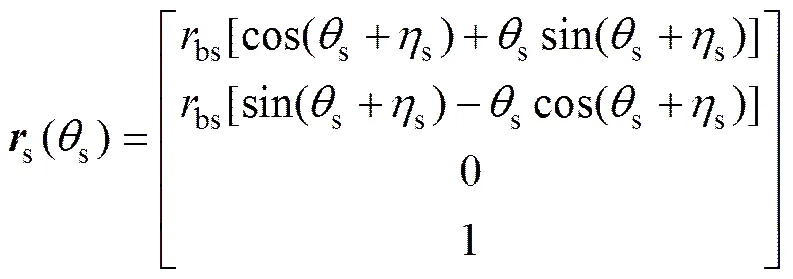
(2)
式中:s和s分别为法截面齿廓上每点的位置矢量及法向量;为渐开线展角参数;为渐开线初始角;bs为虚拟小齿轮的基圆半径。

图3 碟形砂轮轴截面齿廓的修形
图4所示为砂轮轴截面齿廓的修形抛物线。从图4可见:对碟形砂轮轴截面的齿廓沿法线方向按抛物线规律修形,即齿廓上任意点s处的修形量为
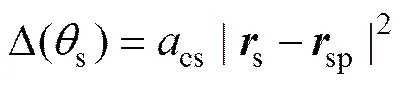
其中:sp为上修形参考点的位矢;cs为修形系数,用于控制修形程度。
修形后碟形砂轮轴向齿廓g的方程为
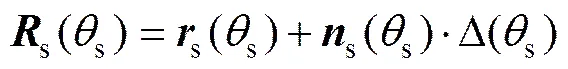
2.2 修形碟形砂轮齿面方程
图5所示为砂轮齿面生成坐标系。从图5可见:将前面修形后的砂轮齿廓表示在坐标系f下,再将其绕d轴旋转则可以得到砂轮的齿面。坐标系d与砂轮固联,坐标系c和s与虚拟小齿轮固联,f为辅助坐标系,为砂轮齿面旋转参数。

(a) 碟形砂轮截面图;(b) 截面旋转运动关系图
前面修形砂轮齿廓在坐标系S下的方程为
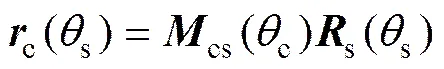
式中:cs为从坐标系s到坐标系c的坐标变换矩阵,为半个齿距角。
砂轮齿面方程可表示为
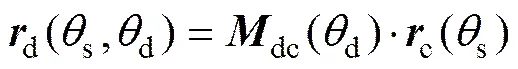
式中:dc为从辅助坐标系c到碟形砂轮坐标系d的坐标变换矩阵。
2.3 砂轮包络面齿轮的坐标系统
砂轮加工面齿轮的坐标系统如图6所示。从图6可见:2与面齿轮固联;d与碟形砂轮固联;t与虚拟小齿轮固联;m,a和g为辅助坐标系;m和a与机架固联;和分别为碟形砂轮和面齿轮的转角,,2s为给定的传动比;0为面齿轮坐标系原点2到虚拟小齿轮坐标系原点t的距离;g为碟形砂轮中心的齿向位置参数(即进给运动参数);d为砂轮中心到虚拟小齿轮中心的距离;∆与∆分别为砂轮在进给运动时,砂轮中心在砂轮固联坐标系d的d轴和d轴方向作抛物线补偿运动的进给量。

(a) 产形齿轮与面齿轮之间的坐标关系;(b) 砂轮的运动坐标系
2.4 无齿向修形的面齿轮齿面
若不考虑齿向修形,即在砂轮作进给运动时砂轮中心在d轴和d轴方向不作抛物线补偿运动,通过砂轮双参数包络的面齿轮齿面记为。在坐标系2中碟形砂轮齿面的曲面族可表示为
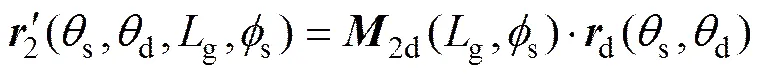
式中:2d为d到2的坐标变换矩阵;和为砂轮齿面参数;g为砂轮沿小齿轮轴向运动参数;为砂轮转动角度参数。
砂轮与面齿轮间的啮合点必须同时满足下面的啮合方程:

(9)
2.5 齿面主动设计与砂轮运动控制
图7所示为面齿轮齿面旋转投影。从图7可见:将齿向未修形面齿轮齿面旋转投影在1个通过面齿轮轴线2的平面上,并在齿面上预置1点来控制接触路径的位置。点可以由以下2个条件确定:1)点位于面齿轮齿宽中点;2) 在齿面包络过程中点与砂轮修形参考点相啮合。以点为坐标原点,建立投影坐标系g,则面齿轮齿面上任意1点在g中的投影坐标为

式中:2,2和2为齿面上任意一点在2中的坐标,2m,2m和2m为点在2中的坐标。
图7 面齿轮齿面旋转投影
Fig. 7 Face gear profile for coordinate system
根据Litvin等[13]提出的局部接触综合法,可以通过预置的位置及接触路径的方向,确定1条完整的接触路径,并通过调整机床加工参数,改善啮合和接触的状态。这里引入倾斜角参数控制接触路径的方向,则接触路径上任1点M满足

从图7还可见:在瞬时接触线L上另取1点K,使K距M的距离为F,F为预置接触椭圆长轴长度。用与M同样的方法求出点,再获得K点处的面齿轮齿面法向量,表示在砂轮固联坐标系d下为,表示砂轮与面齿轮在K相接触时对应砂轮齿面的法向量。
通过沿面齿轮齿面上的瞬时接触线L方向对齿面进行齿向修形。以M点为抛物线修形顶点,取K处的法向修形量为,这里取GLEASON公司推荐值0.007 62 mm[4]。为了达到修形效果,在砂轮沿齿向进给运动过程中,令砂轮中心在砂轮固联坐标系d的d轴和d轴方向作抛物线补偿运动来实现。
引入碟形砂轮中心的补偿运动可表示为

式中:f为齿向修形抛物线系数;为修形方向参数;g0为抛物线顶点位置参数。
已知K点处的法向修形量为,将其分解到齿面上该点法向量dki的各个方向上。则有
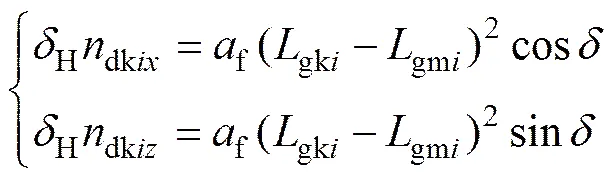
其中:gki与gmi分别是K点和M点对应的砂轮齿向运动参数;dkix与dkiz是砂轮与面齿轮在K点接触时砂轮齿面的法向量分量。
则可以确定3个抛物线运动参数
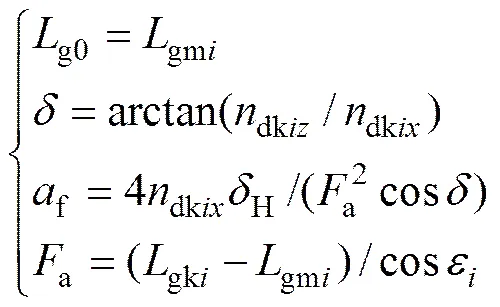
根据上述3个参数控制砂轮中心的运动轨迹,可以将砂轮摆角为时对应的面齿轮齿面上瞬时接触线L以M点对称修形。依次变化砂轮安装角度,控制砂轮进给并在和轴上作补偿修形运动,则可实现预期方式的齿向修形,得到齿向修形后面齿轮齿面。
3 优化传动误差
3.1 轮齿接触分析
轮齿接触分析是将2个连续啮合齿面的啮合过程进行计算机模拟,以获得2齿轮的啮合性能。图8所示为齿面接触分析坐标系统。图8中:1和2分别与标准小齿轮和面齿轮固联;f为整体固定坐标系;a和b为两辅助坐标系;∆为面齿轮的轴向安装误差;∆为偏置误差;为轴交角误差。
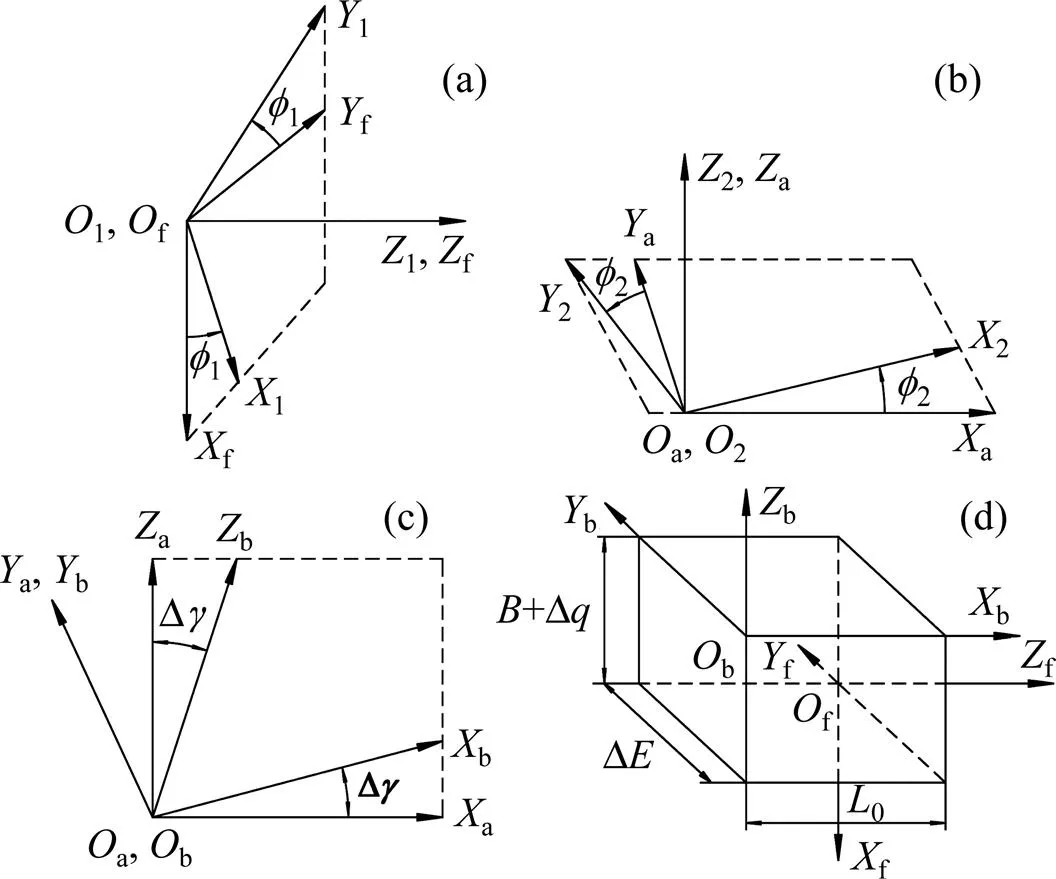
(a) 坐标系S1与Sf;(b) 坐标系S2与Sa; (c) 坐标系Sa与Sb;(d) 坐标系Sb与Sf
通过坐标变换将修形面齿轮和小斜齿轮变换到坐标系f下,则有
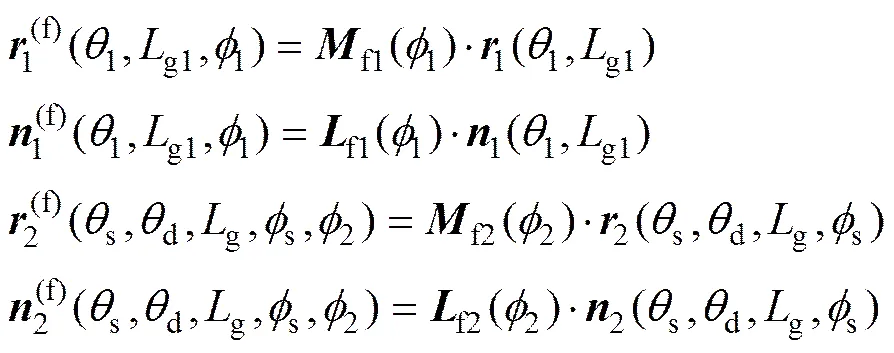
根据齿轮啮合原理[14],修形面齿轮和圆柱齿轮进行点啮合传动,在啮合传动过程中满足以下方程:
(16)
在上述的方程中,可以通过分解得到包含7个方程的非线性方程组,通过给定一系列,代入方程组(16)进行求解,则可以得到每1个相对应的和。
3.2 传动误差曲线优化

由于实际传动误差曲线一般为2次以上(含高阶项,如3次项、4次项)曲线,因此,难以通过双参数控制实际传动误差与预置传动误差曲线的吻合,本文通过双层优化法对传动误差曲线进行优化。在内层优化中,使传动误差曲线2侧幅值尽可能相等,因而建立幅值对称度目标函数:

图9 传动误差曲线优化
Fig. 9 Optimization for transmission errors curve
在外层优化中,令传动误差曲线最大幅值等于预设值,可通过抛物线形状优化参数来调节传递误差曲线的幅值。建立幅值吻合度目标函数:

在每1层优化计算中都只有1个优化设计变量,因此,使用一维优化计算程序即可求解式(18)及式(19)。
4 算例分析
由本文作者方法对某一直齿面齿轮齿面进行设计,与标准小齿轮进行轮齿接触分析,其齿轮副的设计参数如表1所示。
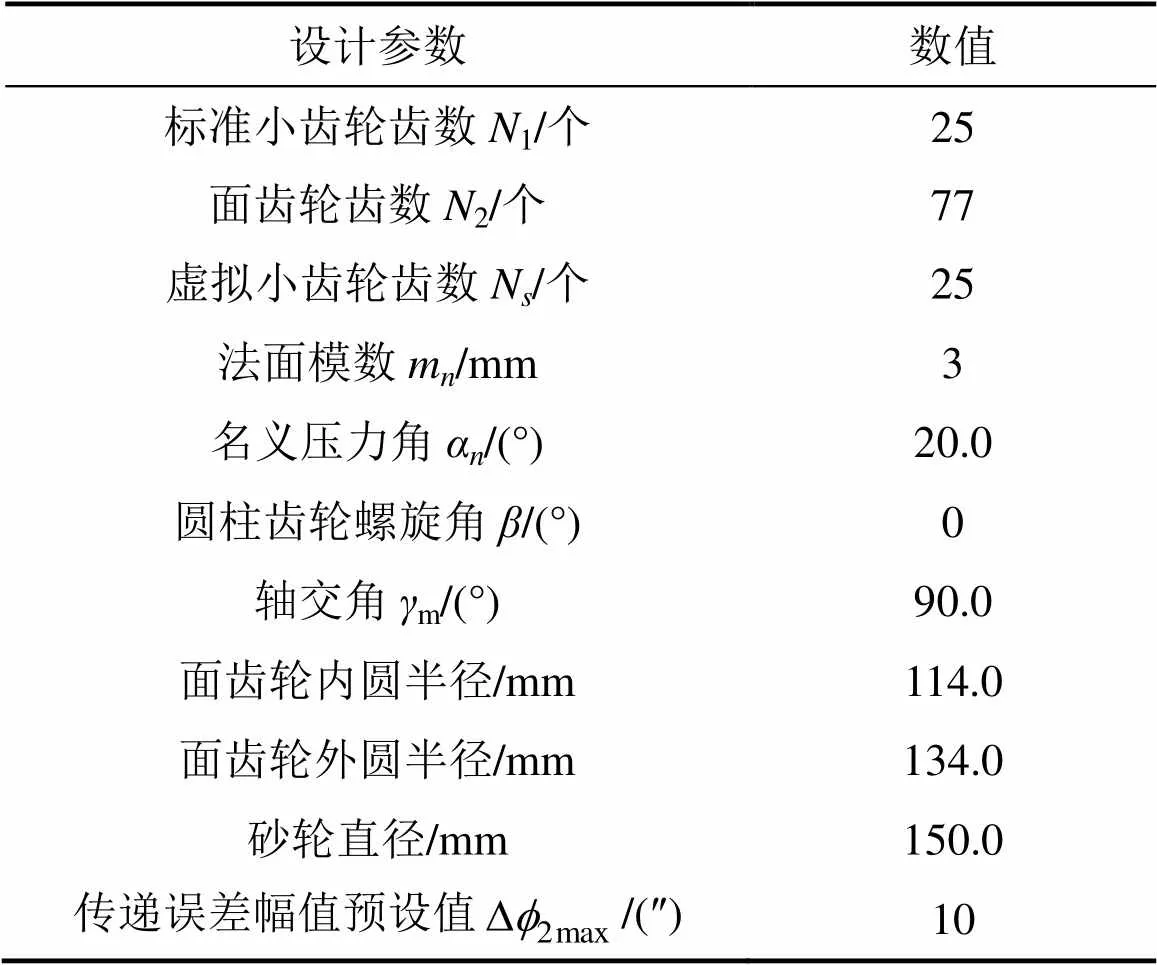
表1 面齿轮副设计参数
通过预置传动误差幅值和接触痕迹进行面齿轮齿面的主动设计,进行齿轮接触分析(TCA),分析结果如图10和图11所示。从图10可以看出:其设计结果中的接触印痕位置和方向基本达到预置要求,该主动设计方法实现了对接触痕迹的控制。从图11可以看出:3种不同情况下的传递误差曲线左右两侧幅值基本相等,非常接近预设值10″。由此可见,该主动设计方法实现了对传动误差曲线的主动设计。

(a) μ=30°, Fa=4 mm; (b) μ=45°, Fa=3 mm; (c) μ=45°, Fa=4 mm; (d) μ=45°, Fa=5 mm; (e) μ=60°, Fa=4 mm.
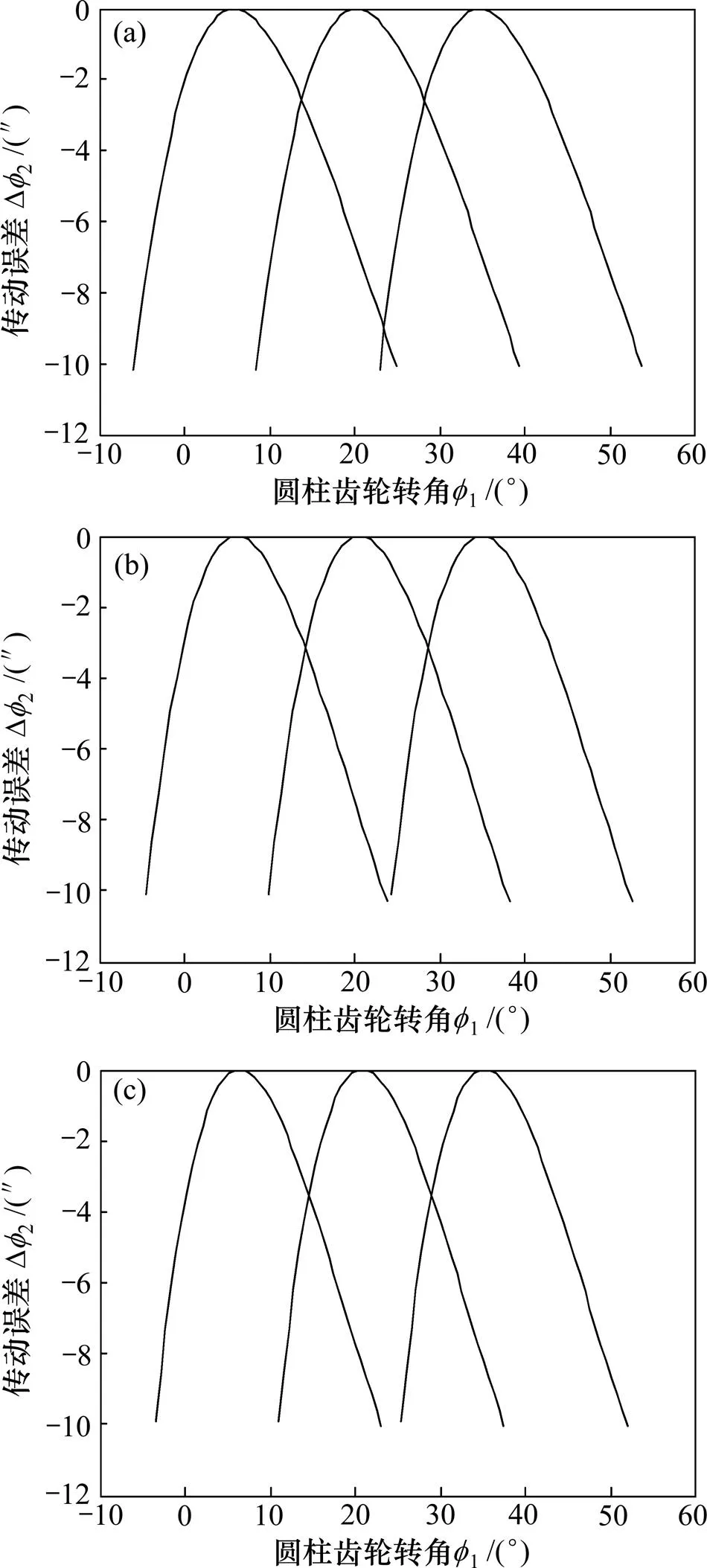
(a) μ=30°, Fa=4 mm; (b) μ=45°, Fa=4 mm; (c) μ=60°, Fa=4 mm.
为了研究和分析该设计方法对安装误差的敏感性,取=30°,a=4 mm,将上述修形后的面齿轮与标准小圆柱齿轮进行有安装误差的TCA分析。令面齿轮轴向安装误差∆=0.2 mm,偏置距安装误差∆=0.05 mm,轴交角安装误差∆=0.05°,其啮合印痕及安装误差如图12所示。由图12可知:经修形后的面齿轮传动避免安装误差下的边缘接触,且啮合印痕的位置和方向对安装误差的敏感性很小;由于安装误差引入了线性的传动误差,会导致传动误差曲线幅值一侧增加,一侧减小。
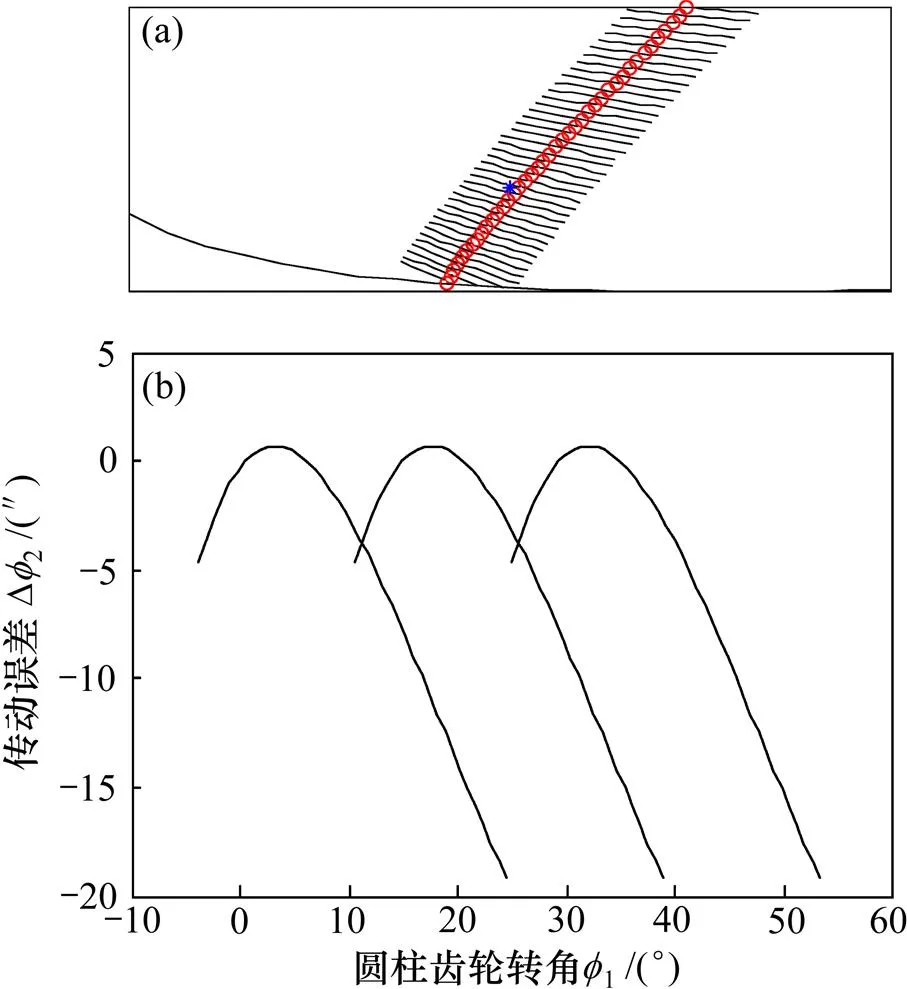
(a) 啮合印痕;(b) 传动误差曲线.
5 结论
1)基于局部综合法和双层优化法建立了面齿轮的主动设计方法。通过对碟形砂轮轴截面齿廓修形量的优化,使面齿轮传动误差满足设计要求;通过齿向的修形优化,使接触印痕的位置和倾斜方向达到预定要求,重合度也得到提高。
2) 主动设计的面齿轮传动避免了边缘接触,且接触印痕对安装误差的敏感性较小,传动误差能够吸收安装误差引起的线性误差。
3) 对面齿轮进行主动设计,达到齿面啮合质量的全程控制,对于高速和重载传动场合具有重要的意义。
参考文献:
[1] Gregory D L, Robert R F, Jie T. Development of face gear technology for industrial and aerospace power transmission[R]. Cleveland (USA): NASA Glenn Research Center, 2002: 1−87.
[2] Litvin F L, Fuentes A, Howkins M. Design, generation and TCA of new type of asymmetric face-gear drive with modified geometry[J]. Computer Methods in Applied Mechanics and Engineering, 2001, 190(43): 5837−5865.
[3] Zanzi C, Pedrero J I. Application of modified geometry of face gear drive[J]. Computer Methods in Applied Mechanics and Engineering, 2005, 194(27): 3047−3066.
[4] Tsay M F, Fong Z H. Novel profile modification methodology for moulded face-gear drives[J]. Proceedings of the Institution of Mechanical Engineers, Part C: Journal of Mechanical Engineering Science, 2007, 221(6):715−725.
[5] Stadtfeld H J. CONIFACE face gear cutting and grinding[J]. Gear Solutions, 2010(9): 38−47.
[6] 彭先龙, 李建华, 方宗德, 等. 采用碟形砂轮的面齿轮磨齿方法理论分析[J]. 航空动力学报, 2012, 27(5): 1159−1165. PENG Xianlong, LI Jianhua, FANG Zongde, et al. Theory analysis for application grinding disk in face gear grinding[J]. Journal of Aerospace Power, 2012, 27(5): 1159−1165.
[7] 郭辉, 赵宁, 侯圣文. 基于碟形砂轮的面齿轮磨齿加工误差分析及实验研究[J]. 西北工业大学学报, 2013, 31(6): 915−920. GUO Hui, ZHAO Ning, HOU Shengwen. Tooth deviation analysis and experimental research of face gear based on disk grinding wheel[J]. Journal of Northwestern Polytechnical University, 2013, 31(6): 915−920.
[8] TANG Jinyuan, YIN Feng, CHEN Xingming. The principle of profile modified face-gear grinding based on disk wheel[J]. Mechanism and Machine Theory, 2013, 70(1): 1−15.
[9] WANG Yanzhong, WU Canhui, GONG Kang, et al. Loaded tooth contact analysis of orthogonal face-gear drives[J]. Journal of Mechanical Engineering Science, 2012, 226(9): 2309−2319.
[10] 李政民卿, 朱如鹏. 面齿轮传动的承载接触分析[J]. 南京航空航天大学学报, 2010, 42(2): 219−223. LI Zhengminqing, ZHU Rupeng. Load tooth contact analysis on face gear driver[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2010, 42(2): 219−223.
[11] 吴训成, 毛世民, 吴序堂. 点啮合齿面主动设计理论和方法[J]. 机械科学与技术, 2000, 19(3): 347−349.WU Xuncheng, MAO Shimin, WU Xutang. On function-oriented design of point-contact tooth surfaces[J]. Mechanical Science and Technology, 2000, 19(3): 347−349
[12] 彭先龙, 胡锡文, 方宗德. 构造拓扑修形齿面的面齿轮传动主动设计[J]. 航空动力学报, 2014, 29(5): 1216−1222. PENG Xianlong, HU Xiwen, FANG Zongde. Active design of face gear drive for modifying ease-off topology flank[J]. Journal of Aerospace Power, 2014, 29(5): 1216−1222.
[13] Litvin F L, ZHANG Yi. Local synthesis and tooth analysis of face-milled of spiral bevel gears[R]. Chicago: University of Illinoist. NASA Office of Management Scientific and Technical Information Division, 1991: 1−20.
[14] 吴序堂. 齿轮啮合原理[M]. 西安: 西安交通大学出版社, 2009: 126−145. WU Xutang. Principles of gear meshing[M]. Xi’an: Xi’an Jiaotong University Press, 2009: 126−145
Tooth surface function-oriented design of face gear based on grinding disk
GUO Hui, XIANG Yunfei, ZHAO Ning
(School of Mechatronics, Northwestern Polytechnical University, Xi’an 710072, China)
A function-oriented design method for face geartooth surface was proposed based onlocalsynthesis method, double-optimization method and the disk wheel generating grinding principle. A predesigned symmetrical parabolic function of transmission errors with given amplitude was obtained by optimization of modification parametersfor thegrinding wheeltooth profile, and a desiredmodificationmode in longitudinal direction was obtained bycontrolling computer numerical control (CNC) multi-axismotions. The results show that this methodenables designers to designthe tooth surface oftheface gearaccording to performance requirements, and to finish processing of face gears on a CNC grinding machine. The function-oriented designmethod canmake thetransmission errorsandtooth contact paths satisfythe design requirements.
face gear; function-oriented design; disk wheel; tooth grinding; contact mode; transmission error
10.11817/j.issn.1672-7207.2015.07.011
TH132.41
A
1672−7207(2015)07−2459−08
2014−06−18;
2014−08−08
国家自然科学基金资助项目(51105307,51075328);陕西省自然科学基金资助项目(2014JM7242);中央高校基本科研业务费专项资金资助项目(3108251511333);高等学校学科创新引智计划项目(B13044) (Projects(51105307, 51075328) supported by the National Science Foundation of China; Project(2014JM7242) supported by the Natural Science Foundation of Shaanxi Province; Project(3108251511333) supported by the Fundamental Research Funds for the Central Universities; Project(B13044) supported by the 111 Project)
郭辉,博士,副教授,从事机械动力学及齿轮几何等研究;E-mail: guohui502@nwpu.edu.cn
(编辑 罗金花)

