连续刚构桥上无缝线路计算模型及方法的简化

王平，谢铠泽



连续刚构桥上无缝线路计算模型及方法的简化

王平，谢铠泽

(西南交通大学高速铁路线路工程教育部重点实验室，四川成都，610031)

为简化连续刚构桥上无缝线路计算模型以及确定正确的简化计算方法，基于原有连续刚构桥上无缝线路计算模型、刚构桥受力特点及梁轨相互作用原理提出新的计算模型。以实际连续刚构桥为例，采用原有计算模型及本文提出的模型分别计算伸缩、制动、断轨及挠曲工况。研究结果表明：在伸缩及断轨工况下，可采用本文提出的简化模型进行计算；对于制动工况，当中支点截面与固结桥墩截面抗弯刚度比值大于4时，采用本文提出的简化模型计算的梁轨相对位移误差可控制在0.2 mm范围内；对伸缩、断轨及制动工况计算可以将变截面刚构桥简化为等截面桥进行简化计算，并且计算结果满足工程需要；对于挠曲工况，由于简化模型未考虑桥墩的偏转因此有较大的误差，因此挠曲工况计算必须采用可以考虑变截面梁及桥墩的整体模型进行计算。

无缝线路；连续刚构桥；计算模型；纵向水平刚度；梁轨相对位移；断缝

连续刚构桥不仅保持了连续梁桥结构刚度大、变形小、动力性能好以及主梁变形挠曲线平缓等优点，也具备了T型刚构桥受力合理的特点。同时由于连续刚构桥施工方法成熟、跨越能力大、对地形地质条件适应性好[1−4]的优点，以及高强预应力钢材、高强混凝土、大吨位张拉锚固体系的应用与发展[5]使其在主跨为100~300 m铁路桥梁中得到较多应用。由于刚构桥梁体为变截面、桥墩与梁体间固结等原因使刚构桥上无缝线路的计算相对比较复杂，也使得分析刚构桥上无缝线路受力及变形时需要依据实际梁体及桥墩的截面参数进行建模并将桥墩与梁体进行耦合。这不仅增加了建模的复杂性，造成程序的通用性不强，也限制模型只能用于桥梁设计完成后对桥上无缝线路受力检算，而不能依据无缝线路受力为桥梁设计尤其是桥墩设计提供指导。本文作者结合刚构墩在被动位移模式下的抗推刚度(以下称为纵向水平刚度)[4]，刚构桥上无缝线路受力特点及原有刚构桥上无缝线路的建模方法对刚构桥上无缝线路的计算模型进行简化，以提高刚构桥上无缝线路建模的效率以及计算程序的通用性。

1 连续刚构桥桥上无缝线路简化模型提出

1.1 连续刚构桥桥墩纵向水平刚度简化

连续刚构桥与连续梁桥的桥墩纵向水平刚度存在一定的差异，主要是由于连续刚构桥桥墩与梁体的固结作用，使得桥墩在发生弯曲变形时会受到梁体的约束作用。因此刚构墩的纵向水平刚度计算不能像连续梁桥桥墩直接简化为悬臂梁的力学模型进行计算，但是其刚度计算公式仍然为

/(1)

式中：为刚度；为作用力；为在作用力下作用点处沿作用力方向的位移。

1个与梁体固结的刚构墩可以简化为图1所示计算模型，图中E为各段梁的弹性模量；G为各段梁的剪切模量；L为各段梁的长度；I为各段梁的惯性距；A为各段梁的截面面积；k为各段梁切应力沿截面分布不均匀而引起的修正系数，其值仅与梁的截面形状有关，对于矩形截面取值为6/5，圆形截面取值为10/9，薄壁圆环截面取值为2[6]。

图1 桥墩刚度计算简图

计算条件为：1=3，为刚构墩弹性模量；1=3，为刚构墩剪切模量；1=3，为刚构墩的长度；1=3，为刚构墩截面惯性距的一半；1=3，为刚构墩截面积的一半；1=3；22=∞；2取较小值，采用力法对超静定结构进行求解，其对应的静定结构示意图如图2所示。

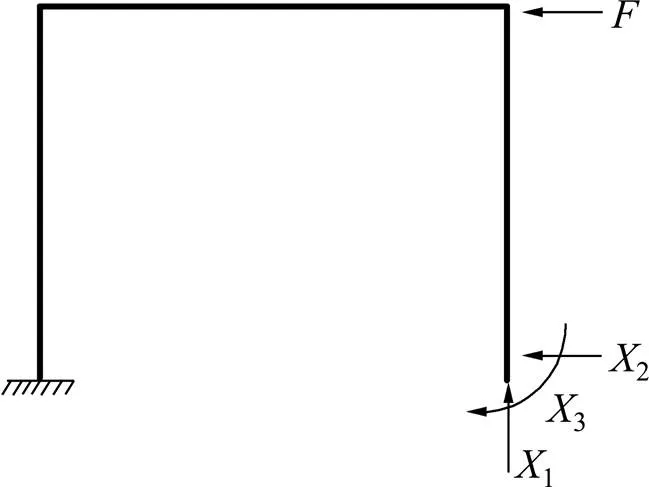
图2 静定结构受力图

因为在图1中2→0，所以桥墩在横向力作用下的位移为

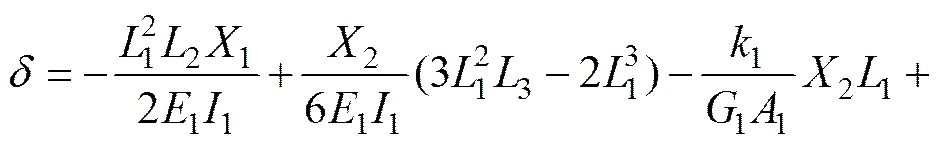
(2)

式(2)适用于桥墩为等截面的情形，图3给出了不同桥墩高度1及桥墩截面惯性矩之半1变化时刚构墩纵向水平刚度与相同条件下连续梁桥墩纵向水平刚度的比值。

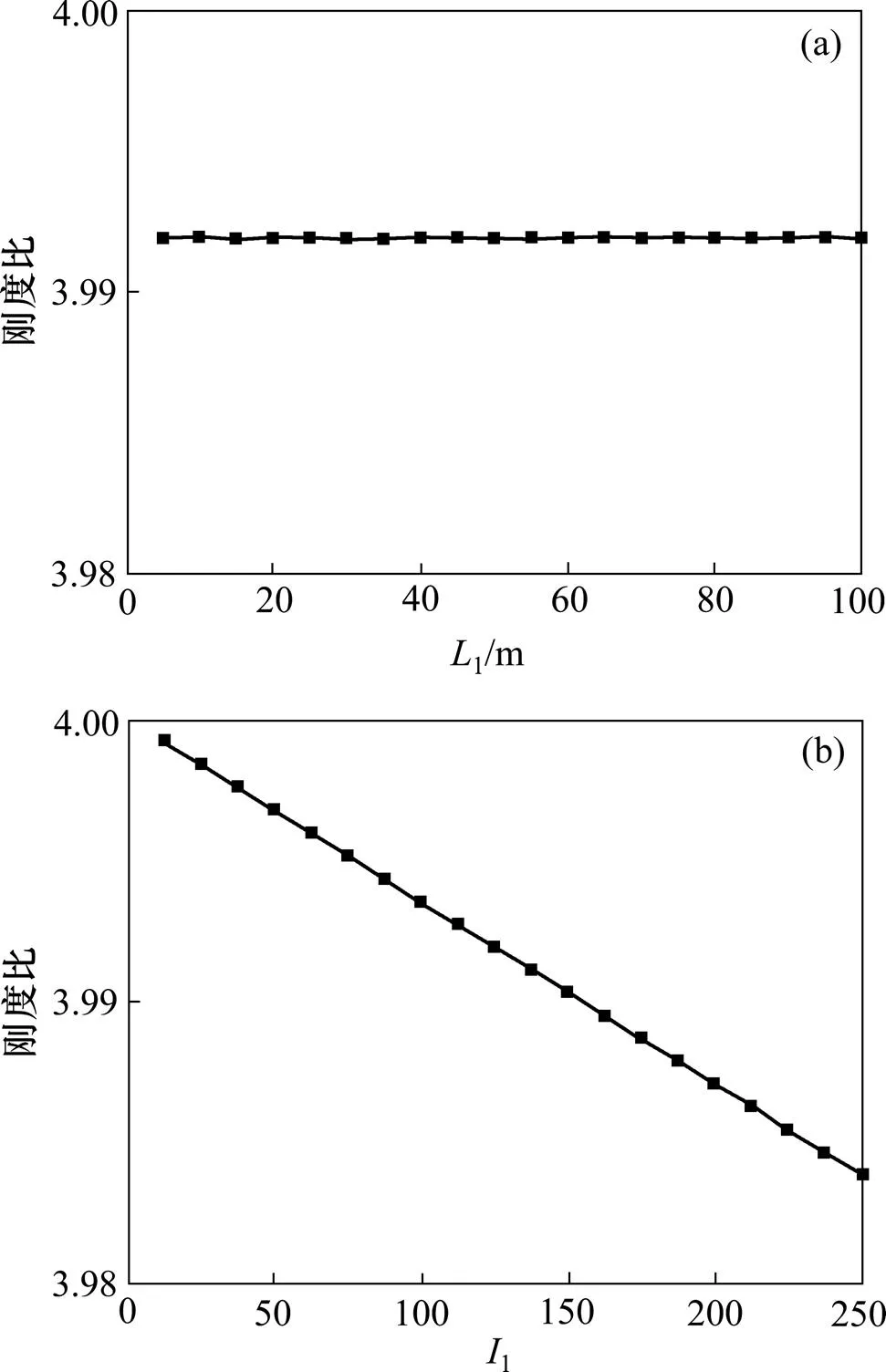
(a) 桥墩高度；(b) 桥墩截面惯性矩

从图3可以看出：单个刚构墩简化后的桥墩纵向水平刚度约为同等条件下连续梁桥墩纵向水平刚度的4倍，该计算结果与文献[4]中简化方法计算的结果是一致的。对于变截面桥墩刚度采用公式计算较为复杂，因此采用有限元方法计算，其得到的结果仍然是刚构桥墩的纵向水平刚度为同等条件下连续梁桥墩纵向水平刚度的4倍。在上面的计算方法中取22=∞，放大了桥梁梁体的约束作用，简化后的桥墩纵向水平刚度稍大，因此需讨论这种简化方法对计算结果的影响。

1.2 刚构桥上无缝线路计算模型

目前普遍采用的刚构桥上无缝线路计算模型如图4(a)所示，其中钢轨采用弹性点支承梁模型，扣件纵向阻力采用非线性弹簧模拟；上下翼缘等效为刚臂用于模拟桥梁挠曲时上下翼缘产生的纵向位移；梁体及桥墩采用梁单元模拟[3, 7−8]。图4(b)所示为本文依据梁轨相互作用原理[9−11]及刚构桥受力特点提出的简化计算模型，该模型主要对桥墩进行了简化，其简化依据为1.1节的计算结果。该简化使模型建立时不需要桥墩的实际截面参数，而可以直接采用设计者提供的桥墩纵向水平刚度进行计算。因此该模型可以在桥梁设计初期，从轨道的角度对桥梁的桥墩刚度提出设计要求，从而方便设计者对桥墩截面尺寸的设计，同时由于对桥墩的简化也使得模拟桥墩的单元从原来的梁单元转变为更为简单的线性弹簧单元。该模型还可以通过设置桥上线路股道数以考虑单线、双线及多线等实际情况，因此，能够更加真实地反映桥上各股道线路受力的状态。该模型采用的单元类型同图4(a)所示的模型相同，且其计算假设同普通桥上无缝线路的计算假设相同，参见文献[12]。

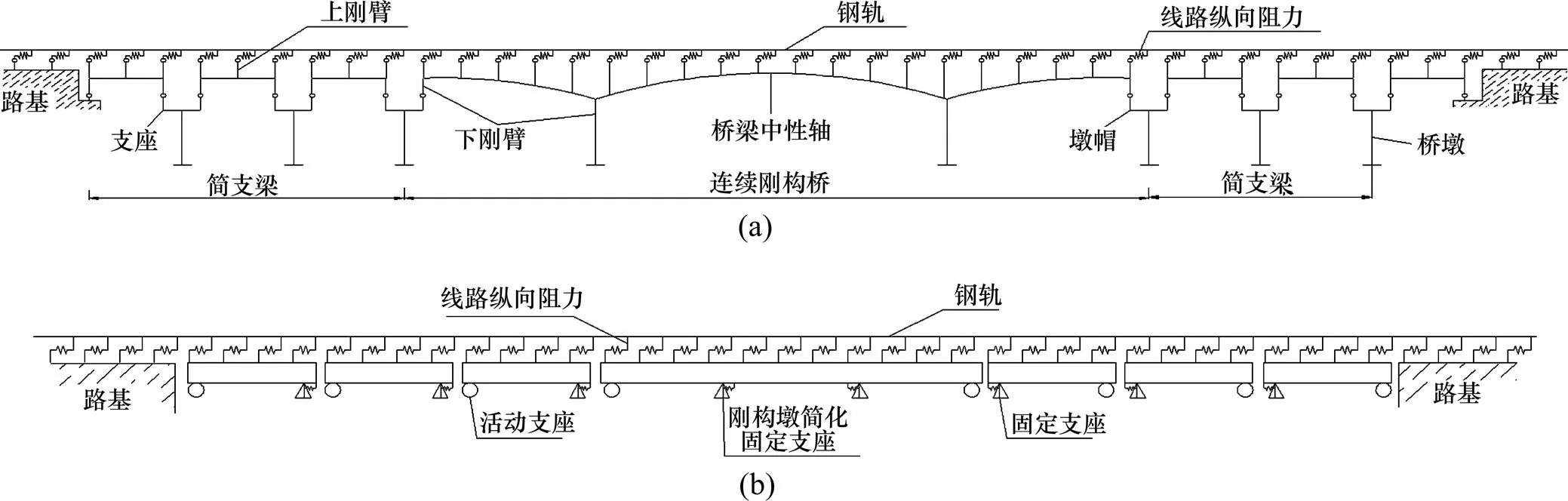
(a) 模型1；(b) 模型2

2 模型计算结果比较

2.1 计算参数取值

以直线上5×32 m简支梁桥+(89+168+89) m连续刚构桥+5×32 m简支梁桥桥上双线有砟轨道无缝线路为例来研究简化计算模型的可靠性，其桥跨及支座布置如图5所示。图5中为边跨支点截面(梁高6 m)、为中支点截面(梁高12 m)、为跨中截面(梁高6 m)，计算中桥梁截面参数均依据设计图纸进行选取。简支梁桥墩刚度采用稍大于规范规定的最小刚度，取为400 kN/cm，单个刚构桥墩纵向水平刚度在设计图中为2 688 kN/cm，与采用1.1节方法计算结果相吻合。计算中为消除边界效应，保证桥上无缝线路处于固定区，简支梁两边的路基长度取为112 m[13−14]。

图5 桥跨及支座布置

钢轨采用60 kg/m钢轨，不考虑钢轨磨耗；全桥不铺设小阻力扣件，因此，线路的纵向阻力即为道床纵向阻力，具体取值依据规范；列车荷载采用中—活载，其中在列车制/启动工况计算时荷载长度取为400 m[15]。在上述计算参数条件下，基于模型1与模型2分别计算伸缩、制动、断轨及挠曲等工况，并进行比较分析。

2.2 伸缩工况

依据TB 10015—2012“铁路无缝线路设计规范”桥上有砟轨道无缝线路在伸缩附加力计算中混凝土梁温度变化为±15 ℃。表1和图6所示为采用模型1与模型2计算的结果。

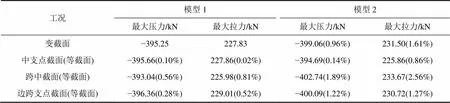
表1 模型1与模型2伸缩工况计算结果

注：表中括号里的数据是相对于模型1变截面工况的相对误差。

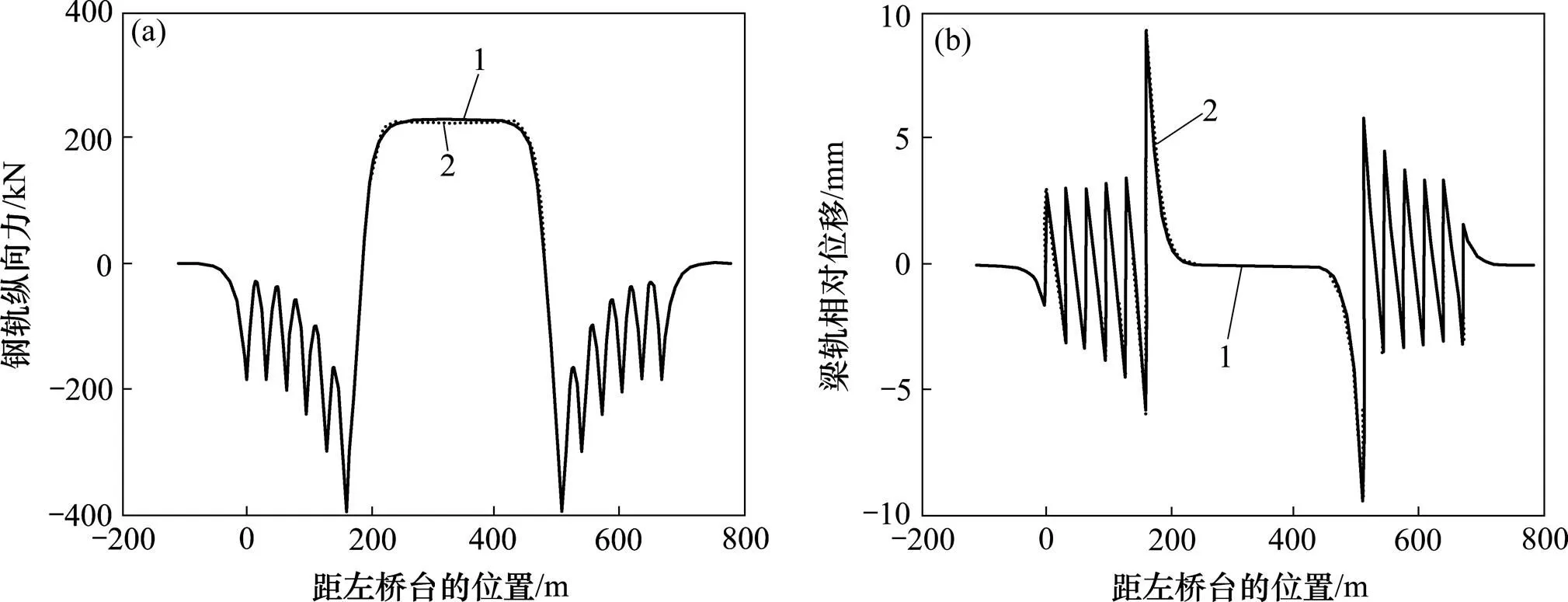
(a) 钢轨纵向力；(b) 梁轨相对位移

由表1和图6可以看出：2种模型均采用变截面梁模型时，模型2计算的钢轨最大压力与模型1计算的最大压力相差0.96%，最大拉力相差1.61%。以等截面建立的3个计算模型中，以中支点截面建立的模型计算的结果与模型1计算的结果相差最小，并且小于变截面梁计算的结果；以跨中截面计算结果相差最大，但是最大压力也仅相差1.89%，最大拉力相差2.56%，均小于5%，满足工程应用的需要。因此，本文提出的刚构桥计算模型可以应用于刚构桥上无缝线路伸缩工况的计算，并且可以简化为等截面梁进行计算。

模型2对伸缩工况计算适用的主要原因为桥墩刚度的变化对伸缩附加力的影响较小(见图7)。由图7可见：桥墩纵向水平刚度从500 kN/cm变化到3 000 kN/cm，纵向压力仅改变了5.3 kN，因此，放大梁体对刚构桥墩的约束作用并不显著影响无缝线路伸缩工况的计算。

1—压力；2—拉力

基于上述分析可以得到：对于伸缩工况可以采用模型2进行计算，并且计算结果误差在允许的范围内，因此，对于2种模型采用等截面简化计算能够满足工程需要，并且以中支点截面进行计算的误差最小。

2.3 制/启动工况

对于桥上有砟轨道无缝线路制动工况的计算主要是检算制动荷载作用下梁轨快速相对位移是否超限，同时该检算项目也是控制桥墩纵向水平刚度最小值的主要因素[16]。对于模型1，从1.1节分析中可知梁体截面抗弯刚度越大，其对桥墩的约束作用就越强，梁轨相对位移就越小。采用模型1与模型2计算制动工况结果如表2所示，其中车头位于伸缩附加力最大位置处即刚构桥左端，列车向左制动且为一线制动。

从表2可以看出：采用模型1计算时随着梁体截面的抗弯刚度的增加，梁轨相对位移降低。由1.1节可知这主要是梁体截面抗弯刚度的增加对桥墩变形的约束作用增加，相当于增加了桥墩的纵向水平刚度，因此梁轨相对位移就会降低。

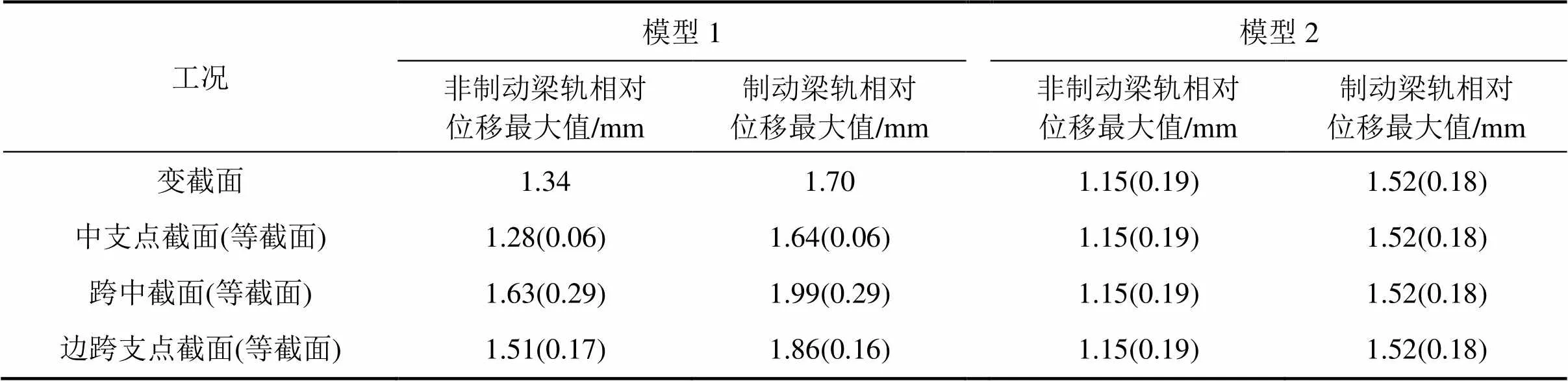
表2 模型1与模型2制动工况计算结果

注：表中括号里的数据表示与模型1变截面工况计算结果之差的绝对值。

当中支点截面惯性矩发生变化时，以模型1为基础，分别采用变截面与中支点等截面计算的梁轨相对位移差如图8所示，在计算变截面模型时跨中及边跨支点截面参数均按照中支点截面参数的改变而等比例变化。

1—非制动轨；2—制动轨

从图8可以看出：随着中支点截面惯性矩的增大，等截面与变截面计算的制动轨及非制动轨的梁轨相对位移差降低，但是差别不大。因此，可以采用中支点的截面代替变截面进行制动工况的计算，且对于刚构墩纵向水平刚度起主要影响作用的是中支点截面。

从表2中模型2的计算结果可见：无论采用变截面还是等截面梁模型计算结果均相差不大，主要是由于制动力对模型2而言仅为纵向力，因此截面的抗弯刚度对结果影响不大。由于桥梁截面面积比钢轨截面面积大得多，因此无论采用梁体的任何截面参数进行计算结果均相差不大。虽然2种模型的计算结果相差较小，但仍有差别，其主要原因是1.1节中桥墩纵向水平刚度推导时假设梁体抗弯刚度无穷大。当梁体截面刚度远大于桥墩刚度时，2种模型能够很好地吻合，下面以模型1为准，通过改变梁体与桥墩的截面惯性矩进行计算，并与模型2计算结果比较，如图9所示。图10所示为中支点截面与桥墩截面惯性矩比值为4时制动工况计算结果的比较图。

1—非制动轨；2—制动轨

从图9可以看出：随着中支点截面与桥墩截面惯性矩比值的增加，2种模型的计算差值愈来愈小，当中支点截面惯性距为桥墩截面惯性距的4倍时，2种模型的计算差值为0.2 mm，小于规范规定梁轨相对位移限值4 mm的5%。因此，当中支梁截面与梁体惯性矩的比值大于4时，可以采用模型2以等截面梁进行简化计算。

由于刚构桥的受力要求等造成中支点截面的抗弯刚度均比较大，而桥墩的截面抗弯刚度较小，对于一般刚构桥，中支点截面与桥墩截面惯性矩比值均能满足大于4的要求，因此，基于模型2采用等截面梁模型计算刚构桥制动工况的结果能够满足工程设计的要求。对于模型1也可以采用等截面代替变截面进行简化计算，为了达到更高的精度，尽量采用中支点截面参数进行等截面计算。由于模型2在制动工况计算中不需要桥墩的具体尺寸，仅需要知道桥墩纵向水平刚度，因此，在桥墩、梁体截面设计中也可以先采用模型2初步计算确定刚构墩的最小水平刚度等，为桥梁设计提供参考，从而降低设计中的反复更改设计的工作，提高工作效率。

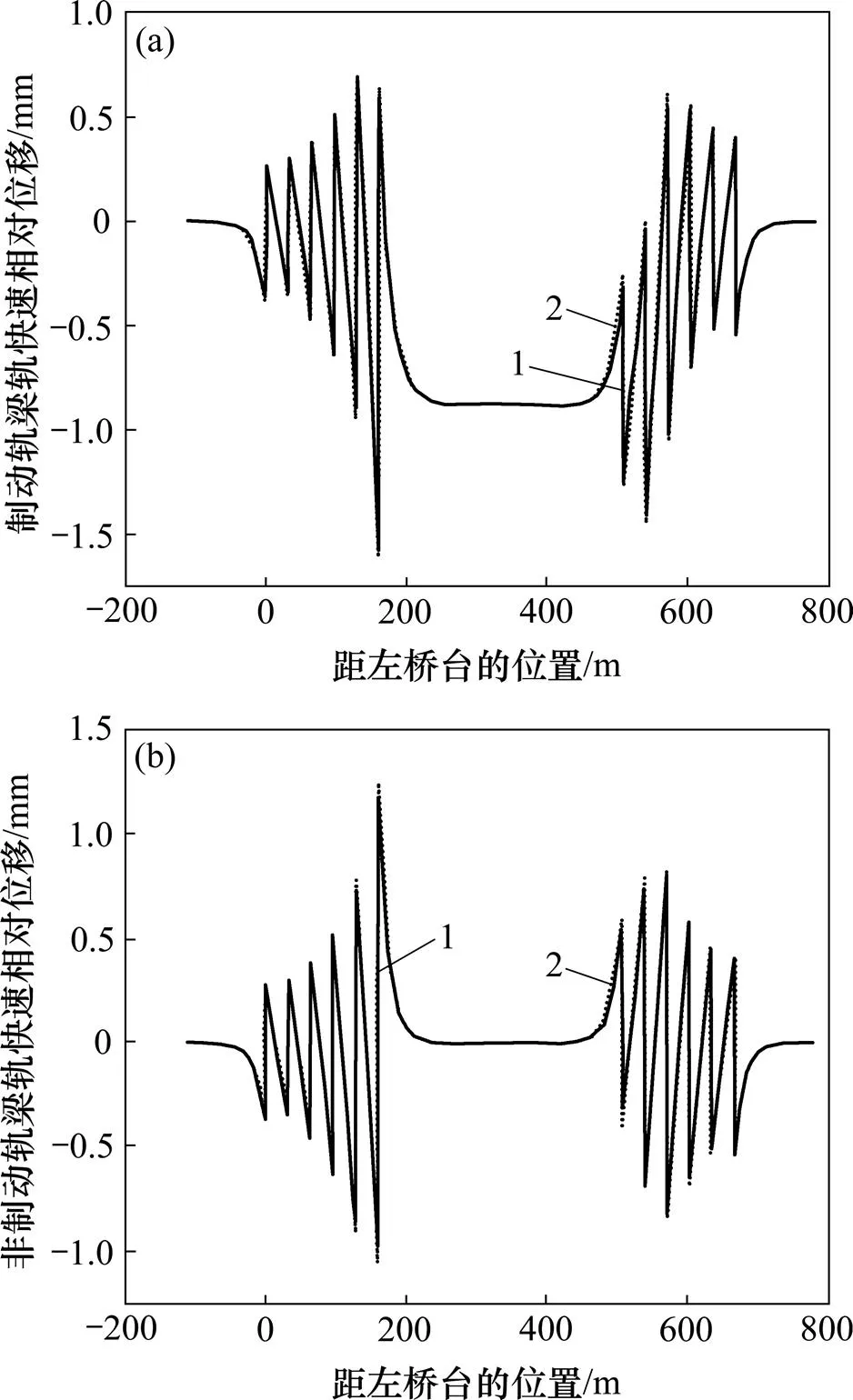
(a) 制动轨；(b) 非制动轨

2.4 断轨工况

为了保证计算的准确性，计算中建立双线4根钢轨，并考虑非断轨的约束作用[17]。计算中以轨温降低50 ℃为例，断轨位置均发生在连续刚构桥左端位置处(伸缩附加力最大位置处)，且只考虑1根钢轨发生断轨，采用模型1与模型2断缝计算结果如表3所示。

表3 模型1与模型2钢轨降温50 ℃时断缝结果

注：表中括号里的数据是相对于模型1变截面工况的相对误差。

从表3可以看出：无论模型1还是模型2计算得到的断缝随截面参数的变化均不大，最大的相对误差仅为0.38%，因此，断缝计算完全可以采用等截面计算的结果代替变截面计算的结果。其主要原因是断缝计算受桥墩刚度的影响比较小，如图11所示。图11是采用模型2计算得到的。

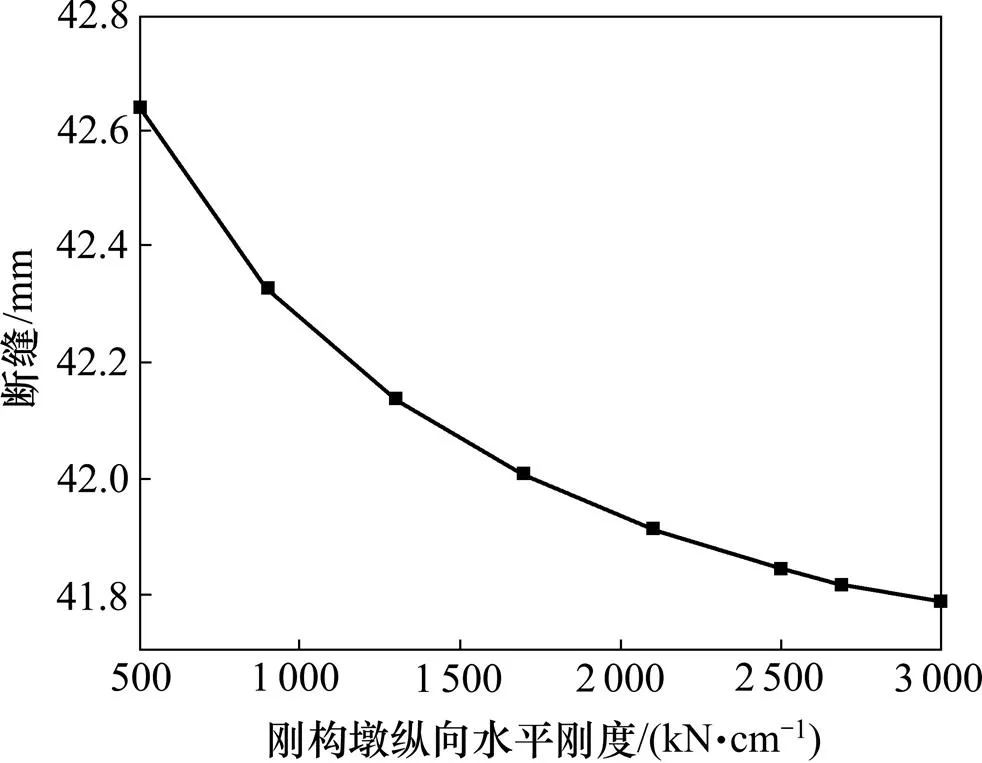
图11 断缝与桥墩刚度关系

从图11可以看出：随着桥墩刚度的增加，断缝逐渐减小，但当刚度从500 kN/cm变化到3 000 kN/cm时，断缝仅改变了0.85 mm；当刚构墩的刚度为2 688 kN/cm时的断缝为41.81 mm，与模型1的变截面断缝相差0.16 mm。因此，刚构桥上无缝线路断轨工况计算可以采用模型2进行计算，并且可以采用等截面梁模型进行计算。

通过上面计算分析可知：对于断缝工况计算可以采用本文提出的简化模型并采用等截面梁进行计算，且计算结果能够满足工程需要，在利用模型1进行计算时也可以将刚构桥简化为等截面梁进行计算。

2.5 挠曲工况

挠曲附加力是桥梁在列车荷载作用下产生挠曲变形，桥梁上下翼缘发生位移，从而引起钢轨中纵向附加力[12]。因此，挠曲计算应该采用变截面进行计算，采用等截面会出现较大的误差。表4所示的计算结果也验证梁体截面特性对挠曲附加力的影响，其中列车荷载从左侧入桥，刚构桥左侧两跨满布荷载，如图12所示。

图12 加载位置示意图

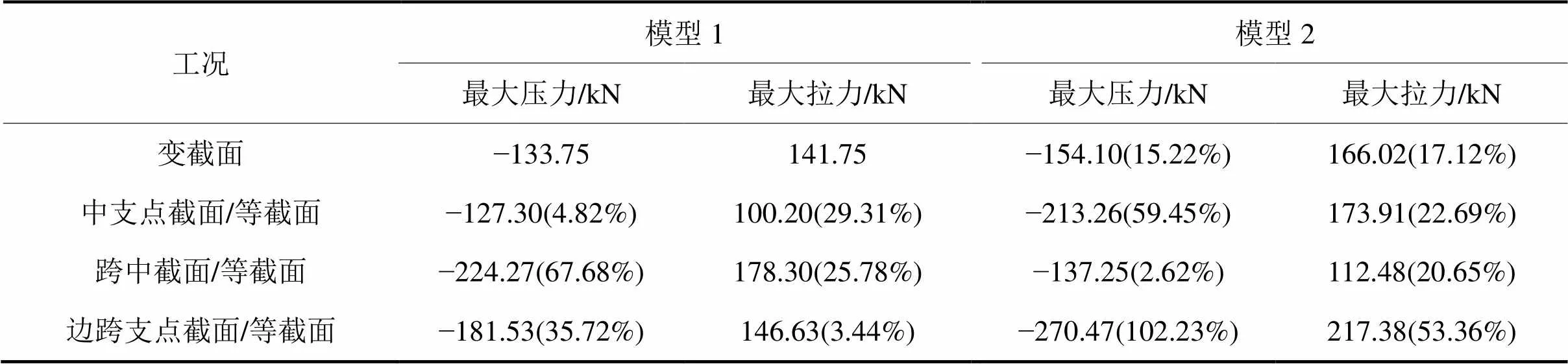
表4 模型1与模型2挠曲工况计算结果

注：表中括号里的数据是相对于模型1变截面工况的相对误差。

从表4可以看出：挠曲工况计算时必须采用变截面梁进行计算，否则会出现较大的误差。图13所示为以变截面为准采用模型1与模型2计算的结果。

从图13(a)可以看出：模型2计算的结果与模型1计算的结果不仅在数值上存在较大差别，而且在车头前方简支梁对应钢轨受力方向上也存在差别，其主要原因是模型2未考虑桥墩偏转，尤其是在列车荷载位于边跨时差别最大，当列车荷载仅位于中跨时这种差别会大幅减小(这里仅为了验证规律取列车荷载仅位于中跨上)，如图13(b)所示。

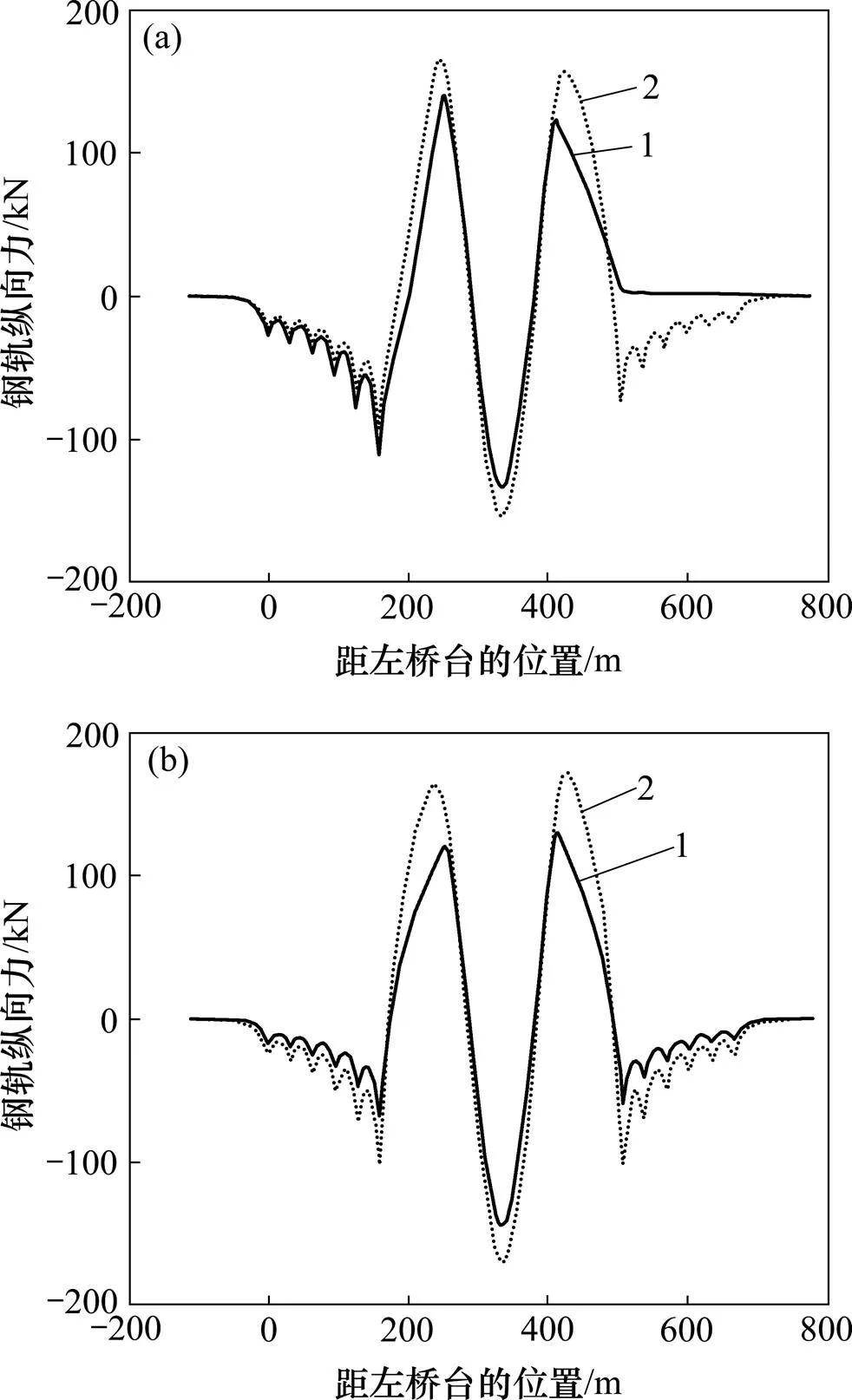
(a) 列车荷载位于刚构桥左侧两跨；(b) 列车荷载位于中跨

从上面2种模型计算的结果分析可知：在挠曲工况计算中必须依据刚构桥实际的截面参数进行建模计算。但是目前新建铁路桥梁一般采用箱形截面构造，因箱形截面整体性好、刚度大、在荷载作用下变形小，静活载作用下挠跨比一般小于1/5 000，因此，挠曲力明显较伸缩力小。从表1与表4的计算结果也可得出这样的结论，因此，桥梁及轨道检算时采用伸缩力，不考虑挠曲力[15, 18−19]。

上述分析表明，本文提出的刚构桥上无缝线路的简化模型不适用于挠曲工况的计算，但考虑到挠曲工况一般不会成为刚构桥上无缝线路检算的控制因素，故本文提出的简化模型具有一定的通用性，且可方便与连续梁桥方案对比。

3 结论

1) 连续刚构桥上无缝线路计算时，对于伸缩及断轨工况，从原理及计算结果均可看出本文提出的计算模型与传统模型并无差异，因此，可以采用本文提出的简化模型进行计算，并且无需建立变截面梁模型，而只需要采用等截面梁进行计算，为了方便，可以采用连续刚构桥的3个特殊断面进行计算。

2) 连续刚构桥上无缝线路制动工况的计算，在满足中支点梁的抗弯刚度为固结处桥墩抗弯刚度的4倍及以上时可以采用文中提出的简化计算模型，能够确保梁轨相对位移误差在0.2 mm范围内。

3) 对于刚构桥上无缝线路，其伸缩、制动及断轨工况可以采用本文提出的简化模型进行计算，计算结果能满足工程要求，并且为设计提出桥墩纵向水平刚度限值，可用于指导桥墩截面参数设计。

4) 连续刚构桥桥上无缝线路挠曲工况的计算必须采用变截面梁模型，并且必须依据桥梁实际尺寸建立整体模型进行计算。

参考文献：

[1] 李民伟. 连续刚构桥梁优化理论研究[D]. 昆明: 昆明理工大学建筑工程学院, 2012: 1−7. LI Minwei. Research on the optimization theory of continuous rigid frame bridge[D]. Kunming: Kunming University of Science & Technology. Faculty of Architecture Engineering, 2012: 1−7.

[2] 马保林. 高墩大跨连续刚构桥[M]. 北京: 人民交通出版社, 2001: 1−17. MA Baolin. Continuous rigid frame bridge with large-span and high-pier[M]. Beijing: People’s Traffic Press, 2001: 1−17.

[3] 张建. 刚构桥上无缝线路的ANSYS分析及二次开发[D]. 长沙: 中南大学土木工程学院, 2007: 48−49. ZHANG Jian. Analysis of CWR on rigid-frame bridge and secondary development of ANSYS[D]. Changsha: Central South University. School of Civil Engineering, 2007: 48−49.

[4] 张永水, 曹淑上. 连续刚构薄壁墩抗推刚度计算方法研究[J]. 中外公路, 2006(3): 144−147. ZHANG Yongshui, CAO Shushang. The study of calculation method of pushing stiffness of continuous rigid frame bridge thin-walled pier[J]. Journal of China & Foreign Highway, 2006(3): 144−147.

[5] 柳学发. 大跨度连续刚构桥的应用和发展[J]. 铁道标准设计, 1999(1): 8−9. LIU Xuefa. The application and development of large span continuous rigid frame bridge[J]. Railway Standard Design, 1999(1): 8−9.

[6] 李廉锟. 结构力学[M]. 4版. 北京: 高等教育出版社, 2004: 141−148, 206−207. LI Liankun. Structural mechanics[M]. 4th ed. Beijing: Chinese High Education Press, 2004: 141−148, 206−207.

[7] 江万红, 唐进锋, 张建, 等. 刚构桥上无缝线路纵向附加力三维有限元分析[J]. 四川建筑, 2012(6): 146−147. JIANG Wanhong, TANG Jinfeng, ZHANG Jian, et al. 3D finite element analysis of additional longitudinal forces transmission between CWR and rigid frame bridge[J]. Sichuan Architecture, 2012(6): 146−147.

[8] 蔡成标. 高速铁路特大桥上无缝线路纵向附加力计算[J]. 西南交通大学学报, 2003, 38(6): 609−614. CAI Chengbiao. Calculation of additional longitudinal forces in continuously welded rails on supper-large bridges of high-speed railways[J]. Journal of Southwest Jiaotong University, 2003, 38(6): 609−614.

[9] Rakesh K, Akhil U. Effect of temperature gradient on track-bridge interaction[J]. Interaction and Multiscale Mechanics, 2012, 5(1): 1−12.

[10] Coenraad E. Modem railway track[M]. 2nd ed. Netherlands: MRT—Productions, 2003: 184−193.

[11] DS804 (B6), Vetschrift for eisenbahnbrchen and sonstige ingenirurbauwerke[S].

[12] 广钟岩, 高慧安. 铁路无缝线路[M]. 4版. 北京: 中国铁道出版社, 2012: 206−207.GUANG Zhongyan, GAO Huian. Welded turnout of railway[M]. 4th ed. Beijing: Press of China Railway, 2010: 203−261.

[13] 谢铠泽, 王彪, 张亚爽, 等. 桥上无缝线路附加伸缩力放散温度及区段的研究[J].铁道建筑, 2012(11): 22−25.XIE Kaize, WANG Biao, ZHANG Yashuang, et al. Calculation and study on additional expansion force dispersion of continuously welded rails on bridge[J]. Railway Engineering, 2012(11): 22−25.

[14] 李秋义, 孙立. 桥墩温差荷载引起的桥上无缝线路钢轨附加力[J]. 中国铁道科学, 2007, 28(4): 50−54. LI Qiuyi, SUN Li. Additional longitudinal force of CWR track on bridge caused by temperature different between one side and another side of pier[J]. China Railway Science, 2007, 28(4): 50−54.

[15] TB 10015—2012, 铁路无缝线路设计规范[S]. TB 10015—2012, Code for design of railway continuous welded rail[S].

[16] 唐乐. 客运专线连续梁桥墩线刚度限值探讨[J]. 铁道工程学报, 2007(S1): 216−219, 224. TANG Le. Discussion of limit stiffness of pier of continuous beam in PDL[J]. Journal of Railway Engineering Society, 2007(S1): 216−219, 224.

[17] 王平, 陈小平. 桥上无缝线路钢轨断缝计算方法的研究[J]. 交通运输工程与信息学报, 2004, 2(2): 47−52. WANG Ping, CHEN Xiaoping. Study on the calculation methods of rail break of CWR on bridge[J]. Journal of Transportation Engineering and Information, 2004, 2(2): 47−52.

[18] 徐庆元, 陈秀方. 连续梁桥上无缝线路附加力研究[J]. 中国铁道科学, 2003(6): 58−63. XU Qingyuan, CHEN Xiufang. Study on additional force transmission between continuously welded rails and continuous beam bridge[J]. China Railway Science, 2003(6): 58−63.

[19] 王平, 刘学毅. 无缝道岔计算理论与设计方法[M]. 成都: 西南交通大学出版社, 2008: 240−294. WANG Ping, LIU Xueyi. The computational theory and design methods of welded turnout[M]. Chengdu: Southwest Jiaotong University Press, 2008: 240−294.

Simplification for calculation model and method of CWR on continuous rigid frame bridge

WANG Ping, XIE Kaize

(MOE Key Laboratory of High-speed Railway Engineering, Southwest Jiaotong University, Chengdu 610031, China)

In order to simplify the calculation model and determine the correctness of simplified calculation method of continuous welded rail (CWR) on continuous rigid frame bridge, a new calculation model based on the original model, mechanical properties of continuous rigid frame bridge and track-bridge interaction was put forward. The new model and original model were used to calculate the expansion, braking, broken rail and bending conditions of CWR on an actual continuous rigid frame bridge. The results show that the new model can be applied to expansion and broken rail conditions; for braking condition, when the ratio of the flexural rigidity of middle support section to that of pier is bigger than 4, the differential of relative displacement between bridge and rail of two models remains less than 0.2 mm; under the condition of expansion, braking and broken rail, it is acceptable to use constant section bridge rather than variable cross-section rigid frame bridge to calculate the force and displacement of CWR in engineering application; under the bending condition, since the new model does not consider the pier deflection, there exists bigger error. So the calculation of bending condition needs building a model which considers the variable cross-section beam and pier at the same time.

CWR; continuous rigid frame bridge; calculation model; longitudinal horizontal stiffness; relative displacement between beam and rail; broken gap

10.11817/j.issn.1672-7207.2015.07.048

U213.9

A

1672−7207(2015)07−2735−09

2014−07−14；

2014−10−17

国家自然科学基金资助项目(U1234201，U1334203) (Projects(U1234201, U1334203) supported by the National Natural Science Foundation of China)

谢铠泽，博士研究生，从事跨区间无缝线路设计理论与方法研究；E-mail: 877057790@qq.com

(编辑 杨幼平)