例析一类物理问题几何关系的简便求法

杨玉良

摘  要：对于带电粒子在圆形匀强磁场区域内的运动问题，几何关系的寻找是求解问题的关键。本文通过轨道对称思想分析，推导出此类问题几何关系的通式。此法不仅能够形象直观地确定运动轨迹，迅速准确寻找几何关系，而且方法容易把握，可以有效消除学生对此类问题的思维、方法障碍。

关键词：轨道对称;匀强磁场;圆形区域;几何关系;通用公式

中图分类号：G633.7 文献标识码：A    文章编号：1003-6148（2015）48-0048-3

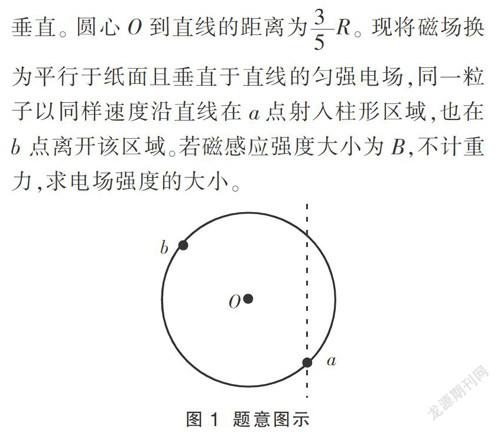
2012年高考理科综合全国卷新课标I物理压轴题：如图1，一半径为R的圆表示一柱形区域的横截面（纸面）。在柱形区域内加一方向垂直于纸面的匀强磁场，一质量为m、电荷量为q的粒子沿图中直线在圆上的a点射入柱形区域，在圆上的b点离开该区域，离开时速度方向与直线垂直。圆心O到直线的距离为R。现将磁场换为平行于纸面且垂直于直线的匀强电场，同一粒子以同样速度沿直线在a点射入柱形区域，也在b点离开该区域。若磁感应强度大小为B，不计重力，求电场强度的大小。

此题研究带电粒子分别在圆形匀强磁场和匀强电场区域内的运动，其物理过程并不复杂，涉及的物理原理也比较简单。解答此题的关键在于带电粒子在圆形匀强磁场区域内运动的几何关系确定，求出带电粒子在磁场中做匀速圆周运动的半径。参考答案给出确定几何关系的解法如下：

如图2所示，过O点和b点作直线的垂线，分别与直线交于c和d点。过O点作直线bd的垂线交于e点。由几何关系知，线段ad、bd和过a、b两点的轨道圆弧的两条半径（未画出）围成一正方形。

因此ad=bd=r （1）

设cd=x，由几何关系得：

ad=ac+cd=+cd=+x=R+x（2）

bd=be+ed=+Oc=+R（3）

联立（1）（2）（3）式得r=R。

笔者认为这种解法稍显麻烦，且学生不易把握。如果抓住带电粒子在圆形匀强磁场区域运动轨道的对称性，将会大大简化几何关系的确定与求解过程。下面提供一种确定带电粒子在圆形匀强磁场区域运动的几何关系的通用公式，现推导如下：

如图3，一半径为R的圆表示一柱形区域的横截面（纸面）。在柱形区域内加一方向垂直于纸面的匀强磁场，一质量为m、电荷量为+q的粒子沿图中直线在圆上的a点射入柱形区域，在圆上的b点离开该区域，粒子入射线的偏心距为d。

画出粒子运动轨迹及相关辅助线如图4所示。显然轨道圆和匀强磁场区域圆相对于两圆的连心线OO1对称。设粒子在磁场中做匀速圆周运动的半径为r，粒子的偏向角为θ，在直角三角形Oac中，Oa=R，ac=d，Oc==。在直角三角形OO1c中，∠OO1c=，=r+d，由三角函数关系得：

tan=（1）

当为-q时，粒子向下偏转，几何关系变为：

tan=（2）

公式（1）（2）为带电粒子在圆形匀强磁场区域运动时几何关系的通式。解题时只要抓住偏向角θ，圆形匀强磁场区域半径R， 粒子轨道半径r，偏心距d等四个量，带入公式即可确定几何关系。用上面推导的公式可以简便确定2012年高考理科综合全国卷新课标I物理压轴题几何关系如下：

设粒子在磁场中做匀速圆周运动的半径为r，题目中粒子的偏向角θ=90 °，粒子入射的偏心距d=R。经过简单分析，本题几何关系适用公式（2），把以上数据代入公式（2）得：

r=R。

下面用以上提供方法分析两道高考物理试题。

例1 （2013年高考全国理科综合课标卷I物理试题）如图5，半径为R的圆是一圆柱形匀强磁场区域的横截面（纸面），磁感应强度大小为B，方向垂直于纸面向外。一电荷量为q（q>0）、质量为m的粒子沿平行于直径ab的方向射入磁场区域，射入点与ab的距离为。已知粒子射出磁场与射入磁场时运动方向间的夹角为60 °，则粒子的速率为（不计重力）（     ）

A.        B.

C.         D.

解析  粒子在圆形匀强磁场区域做匀速圆周运动，根据运动轨道对称性，画出运动轨迹如图6所示。设圆周运动的轨道半径为r，粒子运动过程中洛伦兹力充当向心力，由牛顿第二定律，得

qvB=m

因粒子射出磁场与射入磁场时运动方向间的夹角为60 °，即粒子的偏向角为θ=60 °。粒子入射的偏心距为d=，本题适用公式（1）。把以上数据代入公式（1）得本题几何关系：

tan30 °=。

联立以上各式得：

v=。

所以，本题的正确选项为B。

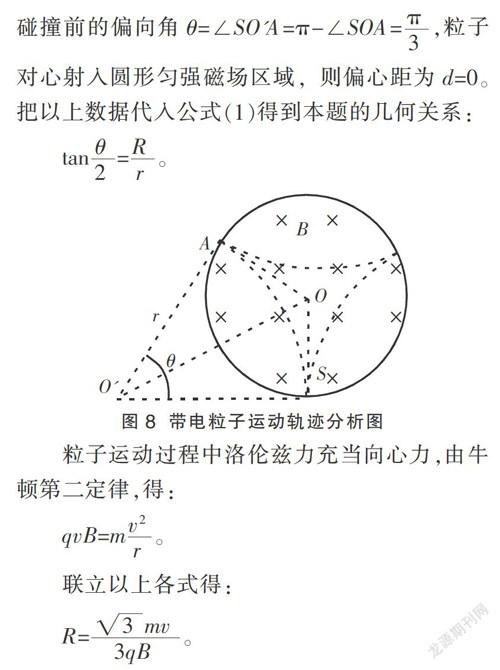
例2 （由2013年高考天津理科综合物理试题改编）一圆筒的横截面如图7所示，其圆心为O。筒内有垂直于纸面向里的匀强磁场，磁感应强度为B。质量为m、电荷量为q的带正电粒子从小孔S以速度v沿半径SO方向射入磁场中，粒子与圈筒发生两次碰撞后仍从S孔射出，设粒子与圆筒碰撞过程中没有动能损失，且电荷量保持不变，在不计重力的情况下，求圆筒的半径R。

解析  粒子进入磁场后做匀速圆周运动，在粒子运动轨道对称性的引领下，画出运动轨迹如图8所示。设运动轨道圆弧半径为r，第一次碰撞点为A，由于粒子与圆筒发生两次碰撞又从S孔射出，则∠SOA=。因此，粒子第一次与圆筒碰撞前的偏向角θ=∠SO'A=π-∠SOA=，粒子对心射入圆形匀强磁场区域，则偏心距为d=0。把以上数据代入公式（1）得到本题的几何关系：

tan=。

粒子运动过程中洛伦兹力充当向心力，由牛顿第二定律，得：

qvB=m。

联立以上各式得：

R=。

由以上解题过程可以看出，抓住轨道对称，就是抓住了分析带电粒子在圆形匀强磁场区域内运动问题的关键。应用轨道对称思想不仅能够形象直观地确定运动轨迹，而且能够用通用公式（1）或（2）迅速准确确定几何关系，方法简便，容易把握。（栏目编辑    陈   洁）