重视中学数学中的一题多解，掌握通性通法

洪庆兵

（西藏拉萨市第三高级中学 西藏拉萨 850000）

重视中学数学中的一题多解，掌握通性通法

洪庆兵

（西藏拉萨市第三高级中学 西藏拉萨 850000）

一题多解，顾名思义，从不同角度、不同渠道来分析问题，探求问题的解法， 最终达到异步同曲的目的它要求教师和学生要认真分析问题， 挖掘问题中的隐含条件， 多角度地探索问题尤其是教师，在设计一题多解的教学之前，要做好大量的准备工作， 尝试着从不同的侧面来解决问题。

在数学教学中， 开展“ 一题多解” 活动， 不仅能使学生加深对知识的理解， 沟通各方面知识的联系， 且能提高解题技能和技巧， 更重要的是有利于发散思维和创新能力的培养在采用“ 一题多解” 时，要注意引导学生从不同角度、不同层次观察和思考， 以便寻求不同解题途径，同时引导学生对各种方法进行比较并注意找出同一问题存在各种解法的条件与原因， 以便总结规律， 从而达到事半功倍的效果。“ 一题多解”是习题课中常用的一种教学方法一题多解， 一方面增强了例题的使用价值，另一方面也培养了学生的发散思维能力，挖掘了学生的创新潜力， 形成了学生的探究意识， 在高考复习中， 一题多解的重要性体现得更为明显笔者根据多年的学习数学专业知识，谈谈对一题多解教学的反思与认识。

人们常说“数学是思维的体操， 科学的皇后”，那么它作为“体操”的作用与“皇后”的价值是如何体现的呢？ 数学解题教学是思维教学的核心， 故可将解题视为二者的集中体现。这也是解题教学受到几乎所有教育工作者普遍重视的原因。近几年来高考数学试题特别注重对中学数学通性通法的考查， 这符合高考命题原则考查基础知识， 注重数学思想， 培养实践能力。中学数学的通性通法是指数学教材中蕴涵的基本数学思想化归思想、转化思想、分类思想、函数方程的思想、数形结合的思想和常用的数学方法数形结合法、构造法、待定系数法、换元法、配方法、反证法等。在高考复习中，要提高数学课堂效率和质量， 精选例题非常重要， 一道好的例题在不同的教学阶段可以用来渗透不同的数学思想。一题多解不仅可以复习数学的通性通法， 同时还能培养学生的发散思想能力。 下面根据这个具体实例，谈谈一题多解数学思想的渗透和数学方法的复习。

1.将最值问题转化为函数值域问题

解法一：通过转化思想，将求最值的问题转化为求函数值域的问题，再利用sin x的有界性得到函数的值域。通过此法也可以让学生弄清值域与最值的区别于联系。

2.将最值问题转化为函数单调性问题

解法二：利用函数性质（奇偶性、单调性、有界性）求最小值的基本方法。本题可以通过转化的思想将问题转化为考察函数的单调性问题，用换元法达到转化的目的。

3.将最值问题转化为基本不等式问题

解法三 ：基本不等式是求最值问题常用的方法。本法巧妙地经过变形构造为适合基本不等式（a2+b2≥2ab）运用的形式，经过两次放缩。注意：在求最值问题时，多次放缩时去“=”号的条件要相同。

4.将最值问题转化为方程根的问题

解法四：根据函数与方程内在的联系，利用转化思想转化为方程的根的问题，进而转化为解不等式问题。

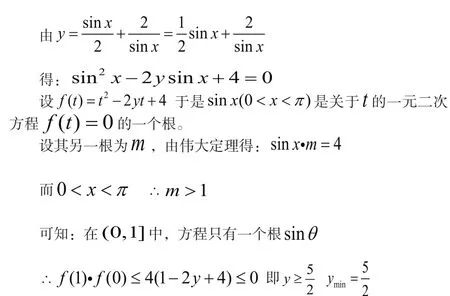
数学题可以是千变万化，但万变不离其中，其根本离不开通性通法的运用和基础知识的应用。题虽然简单，但通过一题多解，我们可以看出其中涵着丰富的教学思想及多种数学常用方法。因此，在我们的教学中，特别是高考、会考复习中，注意一题多解挖掘题的内在关系，可以达到以少胜多、融会贯通的效应，对学生掌握通性通法很有易处。