考虑交通能源消耗的出行需求管理策略研究

张卫华,陈俊杰,江 楠

(1.合肥工业大学交通运输工程学院,安徽合肥230009; 2.同济大学道路与交通工程教育部重点实验室,上海201804)

考虑交通能源消耗的出行需求管理策略研究

张卫华1,陈俊杰1,江 楠2

(1.合肥工业大学交通运输工程学院,安徽合肥230009; 2.同济大学道路与交通工程教育部重点实验室,上海201804)

本文综合考虑出行者出行行为、交通系统运行状态及交通系统能耗之间的关系,建立公交车和私家车双模式下的随机用户均衡模型以及交通系统达到平衡状态的总能耗模型.结合交通系统外部效应的特点和道路收费的经济学原理,以最小广义费用为上层目标函数,建立考虑能耗的双层规划模型,阐明了出行需求管理政策通过调节出行行为来控制交通能耗的机理.将交通政策抽象化代入所建立的双层规划模型.算例分析表明,该模型能够定量地反映实施道路拥挤收费和公交优先措施等策略在不同交通需求情况下对交通能耗的影响.

交通能耗;随机用户均衡;出行需求管理;道路拥挤收费;公交优先

1 引 言

随着社会经济的快速发展,我国交通系统的能源消耗逐年增加[1],如不加以控制,将会严重制约未来城市的健康发展[2].降低交通能耗、减轻排放污染的方法日益成为学术界研究的焦点[3,4].

近年来,越来越多的学者提出“可持续发展的交通”概念,将交通排放和拥堵并称为交通系统的“外部效应”,看作是一种对其他人而言无法补偿的负产品,并对交通公平性进行了研究.王炜等提出了交通系统能耗分析方法,并对交通污染造成的环境影响进行了研究[5].Yin等提出了考虑排放的双层规划模型及减排策略[6].Sugawara等从理论上推导了基于排放最优的出行分配模型以建立最优的碳排放方案,并在不同拥挤等级的道路网进行了实验[7].杨文国等研究了考虑环境因素的交通配流问题[8].Johansson-Stenman等认为间接的环境成本往往被大多数的道路收费模型所忽略,为此他们提出了考虑了环境因素的静态收费模型[9]. Sharma等认为道路收费对温室气体的减排效用通过两条路径达到:首先道路收费鼓励出行者选择更加绿色环保的出行方式,其次道路收费能够合理分配出行者的出行路径,减少拥堵,进而减少排放[10].张华歆等研究了考虑公平性原则的道路拥挤收费问题及确定收费路段的依据和方法[11].Long等从数学模型的角度研究了动态出行者最优情况下的路径选择问题[12].吴丽荣等考虑了交通运输过程中配送车辆燃料消耗的影响因素,构建了考虑能耗的路径问题模型[13].

诚然,增加交通供给可以暂时缓解交通拥堵,但是也会刺激交通需求的进一步增长,并非长久之计[14].出行者根据道路交通条件和交通环境以及具体的交通状况来决定如何出行.而城市交通管理者需采取各种措施以维护交通系统的正常运行,不仅要满足日益增长的交通需求,还应考虑其对能源消耗以及环境的影响,实现可持续发展[15].通过交通需求管理措施,合理地引导、优化出行者的交通行为,不仅可以减少交通拥堵,而且可以减少交通系统能耗,也是实现城市交通可持续发展的关键.因此,本文从出行者出行行为着手,研究私家车和公交车双模式下交通网络配流问题,构建考虑交通能源消耗的广义费用函数,并以此为基础建立双层规划模型,分析道路拥挤收费及公交优先管理策略的节能效果.

2 考虑能耗的随机用户均衡交通网络配流分析

20世纪50年代初学者Wardrop提出了交通网络平衡的第一原理和第二原理,即用户平衡原则与系统最优原则,为交通流分配理论的发展奠定了基础.城市混合交通配流问题涉及到不同交通方式的交通流量在路网上分配,其基础是出行者的出行选择,可采用离散选择模型对其进行分析.结合现实情况,出行者对路网中各路段广义费用的估计不可能完全正确,因此,采用logit模型来描述这种方式选择和路径选择的随机性.

2.1 双模式下广义出行费用函数

出行者在选择路线或交通方式时,通常会权衡不同出行方案所需消耗的时间和成本.除此之外,还需要考虑能耗带来的费用问题,至少对使用私家车出行的人来说,能耗成本不可忽略.所以在研究私家车和公交车双模式均衡分配问题时,出行者将会考虑到的私家车出行成本中包括能耗成本,而对于出行者而言公交车出行成本不包括能耗成本.

对交通网络[N,A]中的出行者不同要求进行均衡考虑,其中N为路网中所有节点构成的集合,A为路网中所有路段的集合,R为交通系统中所有OD对的集合.将能耗、行程时间以及可能的道路收费进行线性加权综合,定义为广义出行费用.由于道路收费和能耗成本容易用价格表示出来,时间成本描述时可以设一个出行者的单位时间价值,令单位时间价值τtime与出行时间的乘积为出行的时间成本.在长度为la的路段a(a∈A)上,私家车和公交车的广义出行费用分别为

其中私家车的广义出行费用C1a包括道路收费,时间成本和能耗成本,而公交车的广义出行费用C2a只包含时间成本,t1a和t2a分别为私家车和公交车通过路段a的时间,τoil是单位体积的油价,e1a是私家车通过路段a的能耗量,ua是对路段a征收的道路收费.

私家车和公交车行程时间采用BPR函数确定,即

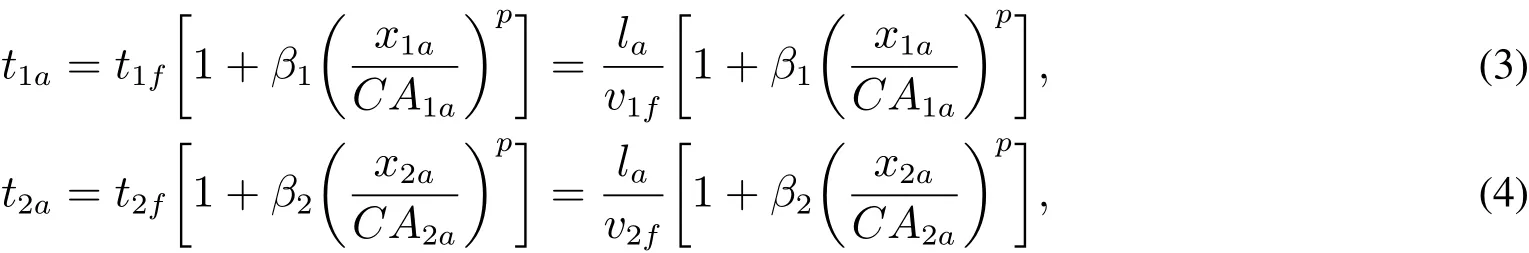
其中x1a和x2a为路段a上两种交通方式的交通量,CA1a和CA2a分别为路段a上私家车道和公交车道的通行能力,t1f和t2f分别为路段a上私家车和公交车为自由流状态下的行程时间,v1f和v2f分别为路段a上两者在自由流状态下的平均行程速度,β1、β2和p是待标定参数.

Chang等建立了一个以理论为基础的时间能耗模型,认为车速小于55km/h时,汽车在一定行程内的油耗与行程时间成线性关系[16].由于该模型的函数关于时间单调递增,结构简单,且在城市道路中,车速在绝大多数情况下小于55km/h,为便于推导,以此作为单车能耗函数.建立私家车和公交车的能耗与行程时间的关系函数如下

其中e1a和e2a分别是私家车和公交车通过路段a的能耗,g1和g2分别是私家车和公交车通过单位长度的路段克服阻力的能耗,h1和h2为大于0的拟合参数.

2.2 双模式下随机用户离散选择模型

假设出行者n的路径选择方案集合为Kin(i=1,2分别表示私家车和公交车),其中任意OD对rs间路径j上交通方式i的广义费用为.设路径j的效用函数为广义费用的相反数,则Uij=−.本着效用最大化原则,当出行者选择路径j出行时,则有

考虑到实际问题中出行者的效用函数很难被精确感知,通常将效用函数分为固定项和随机项,即

其中εij为随机项,数学期望为0.所以有固定项Vij=E(Uij)=−

路段与路径的广义出行费用关系如下

出行者n选择路径j出行的概率为

路径j上两种交通方式的交通量分别为

其中m1与m2分别为私家车和公交车的载客数和分别为OD对rs间两种交通方式的出行需求量.

出行者路径选择的离散模型方程中仍然有两个未知数,即私家车和公交车的流量.采用方式划分模型将私家车和公交车的流量从总流量中划分出来,较为经典的方式划分模型为[17]

其中qrs为OD对rs间的总需求量,θ为待定参数,和分别为私家车和公交车在OD对rs间的最小广义费用

由此可得

2.3 双模式下随机用户均衡模型

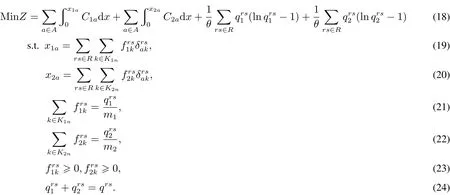
约束条件式(19)与(20)为两种交通方式的路段流量和路径流量的关系;式(21)与(22)表示路径流量与出行需求量之间的关系;式(24)为私家车与公交车双模式下的OD需求量守恒关系.

对该模型进行等价性分析可知,这是一个极小值问题,对数学规划问题,任意局部极小值解满足一阶条件.如果该模型的一阶条件满足路径流量、方式选择等式,则说明用户平衡的要求成立,问题的一阶条件即为拉格朗日函数的极小条件.

一阶条件为

经推导可以得出:上述极小值问题的解既满足logit方式划分模型,又满足Wardrop均衡原则,因此极小值模型的解就是所需要的结果.此外,可以证明目标函数Z为严格凸函数,其约束条件构成凸集,我们知道,凸规划问题的局部最优解亦是全局最优解,因此下层随机用户平衡模型具有唯一解,通常利用Frank-Wolfe算法去求解.

3 考虑交通能耗的双层规划模型

道路拥挤收费能够合理分配出行者的出行路径,引导出行者使用大容量公共交通出行,进而缓解拥堵,减少能耗和排放.体现在道路拥挤收费能够通过影响出行时段和路径选择从空间及时间上优化交通流量的分布,降低过量的出行需求[18].根据边际成本定价理论以及道路收费的经典经济学原理,结合交通管理的决策特点,使用双层规划模型来分析随机用户均衡模式下的道路收费问题.

3.1 模型建立

模型的上层代表管理者通过制定政策达到考虑能耗和延误的广义费用最小的目标,下层代表出行者对政策的反应.模型的核心在于,有一部分人意识到城市交通网络中出行成本与能耗有关,会选择能耗较小的出行方式或者路径,通过牺牲出行时间来减少能耗,达到广义出行费用最小的目标.

由上文分析可知,当路网处于平衡状态时,即可知道私家车与公交车在特定OD对中不同路径的均衡流量值,通过流量值可以得到在此平衡状态下的能耗值.显然能耗值与不同交通方式在不同的路径上的流量相关.当私家车和公交车在不同路径上的流量确定的情况下,路网的总能耗为

式(27)建立了交通系统能耗与交通流运行状态间的关系.

上层模型兼顾能耗因素和时间因素对管理者决策的影响,可表示为

上层模型中未知数x1a和x2a反应了不同路段上两种出行方式的交通量,可通过求解下层模型得到,下层模型即为双模式下随机用户均衡模型.

3.2 算法设计

一般来说,使用精确的数值算法来解决双层规划问题不太现实,通常使用随机搜索技术求解,如退火算法及遗传算法.此双层规划模型的复杂之处在于需要同时达到管理者目标函数最小化、设定考虑能耗的道路收费值以及考虑出行者对此收费值的反应.鉴于遗传算法在解决大规模非线性的最优化目标时更加有效,所以上层模型使用遗传算法求解,下层模型使用Frank-Wolfe算法求解.

设计算法如下:从上层规划开始,首先输入包含了路网细节、需求矩阵、通行能力、路段广义费用方程、行程时间方程、能耗成本方程等.创立初始的道路收费向量作为种群,这些初始的道路收费向量将被加入到广义出行费用矩阵中,作为初始出行费用的一部分.下层模型通过Frank-Wolfe算法求解,下层模型输出公交车和私家车的路段流量矩阵,将其导入BPR函数及能耗函数去计算路段行程时间以及能耗.这样总时间及总能耗就是各路段上不同交通方式的时间和能耗之和.进而得到上层模型目标函数的值,将其作为当前代,并检验约束情况及适应度函数.如此反复计算,直至产生最优解,最后输出的数值分别为目标函数值、最优收费向量、路段行程时间以及能耗.其中,Frank-Wolfe算法步骤如下:

步骤1给定初始流量矩阵ν∈D(D为下层模型的可行域),允许误差ε>0,迭代次数k=0;

4 考虑交通能耗的管理策略算例

为了达到一定的节能目的,管理者需要根据交通情况,制定不同需求管理政策,如道路收费、公交优先以及征收燃油税等.这些政策的目标与手段不尽相同,效果也不同.下面以两个典型案例,定量分析不同政策对城市交通能耗的影响.

4.1 不同出行需求下道路收费对交通能耗的影响

首先计算不同交通需求下,道路拥挤收费政策对道路分担率、公交分担率及平均出行能耗的影响.选取4个不同的总交通需求值,先用随机用户均衡模型算出4种不同总交通需求在无道路收费情况下的平均能耗.再利用双层规划模型算出进行了道路收费后,达到系统最优情况下的平均能耗.

建立简单路网(见图1),此路网有1个OD对1–4,有5条路段,长度分别为l1=l5=2km,l2=l4=4km, l3=3km.私家车和公交车路线的通行能力分别为500 pcu/h和50 pcu/h.v1f和v2f分别为私家车和公交车在自由流状态下的平均行程速度,结合实际情况,取v1f=60km/h,v2f=30km/h;p,β1和β2是BPR函数中待标定参数,取p=3,β1=0.6,β2=0.8;下层模型参数取θ=1;h1和h2为Herman模型的拟合参数,取h1=0.6,h2=3;g1和g2分别是私家车和公交车通过单位长度的路段克服阻力的能耗,取g1=0.1L/km, g2=0.5L/km;m1与m2分别为私家车和公交车的载客数,取m1=2,m2=40;取单位时间价值τtime=100,单位体积的油价τoil=8.

图1 路网示意图Fig.1 The sketches of the road network

计算结果如表1所示:

表1 不同出行需求下道路收费效果Table 1 The effect of road pricing with different travel demand

通过数据分析可知,平均出行能耗与需求量呈正相关关系,需求量一定的情况下,公交车的分担率越高则平均能耗越小.实施道路收费后,抑制了部分私家车出行需求,私家车出行分担率下降了25.70%到31%不等;更多人选择公交出行,系统总能耗有明显下降,实施道路拥挤收费的节能效果显著,平均能耗相应降低了22.51%到25.12%不等.此外,分析发现,道路收费可以均衡路网中不同道路上的私家车交通量,充分利用道路资源,更好地体现交通公平性原则,这反映了道路拥挤收费能够合理引导出行者的出行行为,让出行者更加理性地去选择出行路径和出行方式.

4.2 公交优先对城市交通能耗的影响

公交车载客率高,相对道路占有率低,因此,实施公交优先政策能够缓解城市道路系统负荷过重的问题,有利于混合交通流分流,是缓解交通资源供求矛盾的有效手段之一.

下面分析在提升增加公交系统通行能力的前提下,实施道路收费与否对公交分担率及道路交通能耗的影响.首先建立的简单路网,如图1所示,此路网有1个OD对1–4,有5条路段,长度分别为l1=l5=2km, l2=l4=4km,l3=3km.研究需求使得公交路线的通行能力提升20%,私家车和公交车路线的通行能力分别为500 pcu/h和60 pcu/h.v1f和v2f分别为私家车和公交车在自由流状态下的平均行程速度,结合实际情况,取v1f=60km/h,v2f=30km/h;p,β1和β2是BPR函数中待标定参数,取p=3,β1=0.6,β2=0.8;下层模型参数取θ=1;h1和h2为Herman模型的拟合参数,取h1=0.6,h2=3;g1和g2分别是私家车和公交车通过单位长度的路段克服阻力的能耗,取g1=0.1L/km,g2=0.5L/km;m1与m2分别为两种交通方式的载客数,取m1=2,m2=40;取单位时间价值τtime=100,单位体积的油价τoil=8;总需求量q=2 000次.得出公交扩容前后道路收费效果对比如表2所示:

表2 公交扩容前后道路收费效果Table 2 The effect of road pricing before and after the improvement of public transit capacity

由表2可以看出,在不实施道路拥挤收费情况下,公交通行能力上升后,公交分担率上升了5.56%,系统平均能耗下降3.95%.配合道路拥挤收费和公交扩容的措施后,公交分担率上升显著,增长率达到60.42%,系统能耗也有明显的下降,平均能耗下降26.54%.这说明,要增加公交车的分担率,仅靠发展公交系统是不够的,还需要有其他措施抑制不必要的私家车出行,合理引导出行者的出行行为,同时,也验证了通过道路拥挤收费能够充分利用公交系统资源,强化公交优先政策的节能效果.

5 结束语

本文研究了不同交通需求管理策略对城市交通能耗的影响,构造以最小广义费用为上层目标函数的双层规划模型,结合数值算例,定量探讨了不同交通需求管理策略的节能效果.得出以下结论:实施道路收费和公交优先策略能够合理引导出行者的出行行为,有效提高公交的分担率,两者联合实施可使系统平均能耗显著降低.为管理者制定节能型交通管理政策提供了很好的理论依据和参考,具有一定的实践意义.我们的研究还存在许多有待改进的地方,交通是一个动态的过程,动态交通分配情况下的交通系统能耗问题将作为后续研究工作的重点.

[1]张卫华,王 炜,胡 刚.基于低交通能源消耗的城市发展策略[J].公路交通科技,2003,20(1):80–84.

Zhang Weihua,Wang Wei,Hu Gang.Strategies on urban development based on low energy consumption of traffc[J].Journal of Highway and Transportation Research and Development,2003,20(1):80–84.(in Chinese)

[2]Chandran V G R,Tang C F.The impacts of transport energy consumption,foreign direct investment and income on CO2 emissions in ASEAN-5 economies[J].Renewable and Sustainable Energy Reviews,2013,24(1):445–453.

[3]Lutsey N,Sperling D.Greenhouse gas mitigation supply curve for the United States for transport versus other sectors[J].Transportation Research:Part D,2009,14(3):222–229.

[4]Liddle B.Urban density and climate change:A STIRPAT analysis using city-level data[J].Journal of Transport Geography,2013, 28(1):22–29.

[5]王 炜,项乔君,常玉林,等.城市交通系统能源消耗与环境影响分析方法[M].北京:科学出版社,2002.

Wang Wei,Xiang Qiaojun,Chang Yulin,et al.Analytical Methods for Energy Consumption and Environmental Impact on City Traffc System[M].Beijing:Science Press,2002.(in Chinese)

[6]Yin Y F,Lu H P.Traffc equilibrium problems with environmental concerns[J].Journal of the Eastern Asia Society for Transportation Studies,1999,3(6):195–206.

[7]Sugawara S,Niemeier D A.How much can vehicle emissions be reduced:Exploratory analysis of an upper boundary using an emissions-optimized trip assignment[J].Transportation Research Record,2002,1815(1):29–37.

[8]杨文国,高自友.考虑环境因素的广义用户平衡和广义系统最优配流模型[J].中国公路学报,2003,16(4):72–76.

Yang Wenguo,Gao Ziyou.Generalized user equilibrium assignment model and generalized system optimization assignment model under environment[J].China Journal of Highway and Transport,2003,16(4):72–76.(in Chinese)

[9]Johansson-Stenman O.Optimal environmental road pricing[J].Economics Letters,2006,90(2):225–229.

[10]Sharma S,Mathew T V.Multiobjective network design for emission and travel time trade-off for a sustainable large urban transportation network[J].Environment and Planning B:Planning and Design,2011,38(3):520–538.

[11]张华歆,周溪召.基于社会与空间公平多用户网络拥挤收费定位[J].系统工程学报,2009,24(2):184–189.

Zhang Huaxin,Zhou Xizhao.Congestion pricing location problem of multi-class network with social and spatial equity constraints[J].Journal of Systems Engineering,2009,24(2):184–189.(in Chinese)

[12]Long J C,Huang H J,Gao Z Y,et al.An intersection-movement-based dynamic user optimal route choice problem[J].Operations Research,2013,61(5):1134–1147.

[13]吴丽荣,胡祥培,饶卫振.考虑燃料消耗率的车辆路径问题模型与求解[J].系统工程学报,2013,28(6):804–811.

Wu Lirong,Hu Xiangpei,Rao Weizhen.New capacity-vehicle-routing-problem model and algorithm for reducing fuel consumption[J].Journal of Systems Engineering,2013,28(6):804–811.(in Chinese)

[14]Rajan S C.Climate change dilemma:Technology,social change or both:An examination of long-term transport policy choices in the United States[J].Energy Policy,2006,34(6):664–679.

[15]孟 梦,邵春福,张 鑫.考虑低碳排放约束的多模式均衡分配模型[J].北京理工大学学报,2012,32(1):7–10.

Meng Meng,Shao Chunfu,Zhang Xin.Traffc assignment model with low carbon emissions constraints[J].Transactions of Beijing Institute of Technology,2012,32(1):7–10.(in Chinese)

[16]Chang M F,Herman R.Trip time versus stop time and fuel consumption characteristics in cities[J].Transportation Science,1981, 15(3):183–209.

[17]SheffY.UrbanTransportationNetworks:EquilibriumAnalysiswithMathematicalProgrammingMethods[M].Englewood:Prentice Hall,1985:262–300.

[18]张小宁.交通网络拥挤收费原理[M].合肥:合肥工业大学出版社,2009:10–25.

Zhang Xiaoning.Theories of Congestion Pricing in Transportation Networks[M].Hefei:Hefei University of Technology Press, 2009:10-25.(in Chinese)

Strategies of travel demand management with transport energy consumption

Zhang Weihua1,Chen Junjie1,Jiang Nan2
(1.School of Transportation Engineering,Hefei University of Technology,Hefei 230009,China; 2.Key Laboratory of Road and Traffc Engineering of Ministry of Education,Tongji University,Shanghai 201804,China)

Taking the relationship between travel behavior,operating state and energy consumption of the transport system into account，a stochastic user equilibrium model with dual-mode of bus and private car has been established.Meanwhile,the total energy consumption model in the equilibrium state of transport system has been derived.According to the characteristics of externality and economic principles of road pricing,a bi-level programming model which regards the generalized cost as the upper objective function has been set up to probe the effect of travel demand management policies on regulating travel behaviors and the energy consumption.Various policies have been abstracted and imported into the bi-level programming models.The example shows that the infuence of traffc energy consuming can be quantitatively refected by implementing road pricing and public transport priority with the model under different traffc demands.

transport energy consumption;stochastic user equilibrium;travel demand management;road pricing;public transport priority

U491.1

A

1000−5781(2015)04− 0566−09

10.13383/j.cnki.jse.2015.04.00？

2013−03−04;

2013−08−19.

国家自然科学基金资助项目(51178158;51308176).

张卫华(1967—),男,安徽宿松人,博士,教授,研究方向:交通规划,E-mail:ahweihua@163.com;

陈俊杰(1989—),女,山西大同人,硕士,研究方向:交通规划,E-mail:amao9188@163.com;

江 楠(1989—),男,安徽黄山人,博士,研究方向:交通规划,E-mail:583962049@qq.com.