可靠性约束下系统全寿命周期成本优化建模

陈光宇,郑舒扬,冯 毅

(电子科技大学经济与管理学院,四川成都611731)

可靠性约束下系统全寿命周期成本优化建模

陈光宇,郑舒扬,冯 毅

(电子科技大学经济与管理学院,四川成都611731)

单纯依据全寿命周期成本最小或系统可靠性最高进行系统设计具有一定的局限性.在系统寿命服从Weibull分布的条件下,给出预防性维修策略,构建设计费用、制造费用和维护费用函数,从而建立可靠性约束下的系统全寿命周期成本的优化模型;接着完整地提出包括系统全寿命周期成本、可靠性设计水平和预防性维修次数在内的系统设计均衡区域的决策方法.最后,以某大型装置的光学系统为例,说明该方法在工程应用上的实效性,也为系统设计均衡区域的决策过程提供系统的思路和方法.

系统设计;可靠性;全寿命周期成本;预防性维修;均衡区域

1 引 言

全寿命周期成本(lifecycle costs,LCC)是系统在预定有效期内发生的直接、间接的费用之和,它是设计、制造、开发、使用、维护、退役等过程中发生的费用的总和[1].全寿命周期成本管理于20世纪60年代源起于美国军方,主要用于军事物资的研发和采购.合理地规划系统全寿命周期成本是非常必要的,比如美国设计的F-16战斗机,运用了LCC方法仔细地比较各种候选设计方案,最终选择了一个尺寸小、重量轻、结构简单和技术风险小的低成本方案.据分析,若F-16的设计不采用此方法,就要多花费42亿美元的全寿命周期成本, F-16的LCC设计既提供了符合要求的性能,又保证了较低的成本[2].近年来,LCC理论在装备和复杂系统领域得到了广泛的研究.¨Oner等[3]建立了受组件可靠性和备件库存水平影响的包括设计费用、制造费用以及维修和停机费用在内的产品全寿命周期成本模型,通过平衡可靠性和基础库存水平使产品的全寿命周期成本最小.Jin等[4]在系统使用度不确定的情况下提出一个解析模型来表示系统的使用可用性,并在系统可用度的要求下研究了机群全寿命周期成本最小和利润最大化条件下的LCC决策模型.Lu等[5]从LCC优化角度研究了电力系统的维护策略,运用机械工程学的退化理论,分析每次维修周期内的故障率,建立优化问题的模型,通过遗传算法得到最优维修策略.Waghmode等[6]提出了一个可修复系统的广义LCC模型,该可修复系统的寿命服从两参数的威布尔分布,采用随机点过程法描述了系统的维护和维修成本,但这篇文章并没有给出维修费用和系统可靠性之间的关系.

随着系统复杂性的增加,其维护和使用费用也日益昂贵,在某些工业领域维修费用在LCC中占据了最大的份额.1962年在美国国防部长的报告中披露:1961年美国国防预算至少25%用在维修费上,并且得出结论认为把全部寿命周期内的维护费压缩到最低才是产品研制的基本思想[7].在多种维修方法中,预防性维修(preventive maintenance)是很有代表性的方法.预防性维修的研究可追溯到20世纪60年代Barlow和Hunter的开创性工作[8].其后,研究者对预防性维修模型进行了扩展和推动.程志君等[9]针对故障信息监测下的多状态劣化系统,其劣化阶段停留时间和检测间隔时间服从一般分布且“修复如新”,利用位相型(PH)分布近似方法,提出系统预防性维修的优化模型及简化求解过程和改进的值迭代算法,解决了同一模型中检测与预防性维修策略综合优化的问题.随着模型复杂性的提高,更多预防性维修的研究考虑了维修成本因素,研究如何以最低的费用保持设备的固有可靠性.韩帮军等[10]提出了等效役龄的概念,建立了预防性维修周期间的故障率递推关系,以威布尔分布为例展开研究,构建了可靠度约束条件下有限时间区间的预防性维修的优化模型,但没有在LCC框架下对系统的可靠性和全寿命周期成本进行优化.

鉴于上述研究的不足,本文从全寿命周期成本优化的角度展开研究,系统投入使用后采用预防性维修策略,即在频繁故障期之前对系统进行维修,以减少随机故障的产生;并考虑预防性维修活动与系统故障率之间的动态变化而非“修复如新”的情况.在系统寿命服从威布尔分布的条件下,引入各预防性维修周期内系统的可靠度作为全寿命周期成本函数的约束条件,构建可靠度约束下的LCC模型,并提出了系统均衡设计区域的决策方法.

2 维修模型

对于造价昂贵、发生故障损失巨大的系统,如果能够根据系统故障的规律,在元件损伤加速之前就将其换下并进行修复,就可大大延长系统的寿命[11].为了预测故障率的变化,韩帮军等在文献[10]中提出了等效役龄的概念,建立了生产系统预防性维修周期间故障率的递推关系.因为该模型能够反映生产设备在这一时间段内维修成本与维修周期之间的关系,可以揭示预防性维修活动与设备故障率之间的动态变化规律.这里借鉴此思路,针对研究对象的特点,做出以下假设.

1)假设系统在寿命区间[0,T]内共进行n次预防性维修,并采用以下的故障控制策略.

a)系统运行到ti时刻时进行第i次预防性维修,预防性维修时间为θi,i=1,2,...,n;

b)当系统在第i个预防性维修周期Ti内出现故障时进行最小维修,小修会使系统恢复应有的功能,但不会改变系统维修后的故障率;

c)系统在故障后或到达预防性维修时间点时能立即进行维修;

d)进行小修的维修时间相对于运行时间很小,可忽略不计;

e)运行使用无停歇.

2)预防性维修的效果采用等效役龄τi和役龄回退因子αi(αi∈(0,1))度量.由于预防性维修降低了系统的故障率,提高了系统的性能,等同系统的役龄时间向前推移了一段时间.设在第i个预防性维修周期后,系统的役龄向前推移了αiTi,则经过预防性维修后相当于系统在第i个周期内只使用了Ti−αiTi,即等效役龄τi=Ti−αiTi.等效役龄τi的递推关系如下

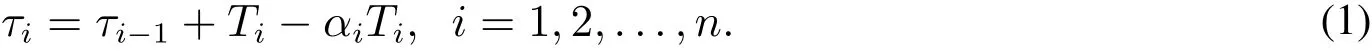
引入役龄回退因子和等效役龄后,则第i个预防性维修周期内发生的故障次数Fi可以表示为

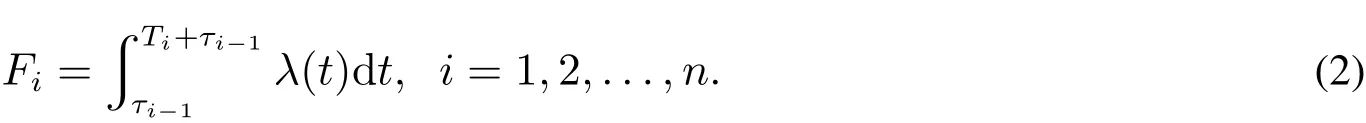
当系统寿命服从威布尔分布时,故障率如下

其中m为威布尔分布的形状参数,故障率函数递增或递减的趋势由m的取值决定:当01时,故障率递增.预防性维修能够减少系统的老化或者磨损,在故障率为常数和故障率递减时,预防性维修对系统可靠性没有任何影响,因此预防性维修主要考虑m>1的情况.η为尺度参数,它影响分布函数的均值和广度,也称离散度,当η增加时,相同时间点上的可靠度递增.

当失效时间服从威布尔分布时,故障次数为

Weibull分布的MTTF可由下式确定.此时，平均失效时间为

由于MTTF表示寿命均值,即系统平均能够正常运行多长时间,才发生一次故障.系统的可靠性越高,平均无故障时间越长.对于高倾斜数据而言,当m较小(小于3)时,可以用MTTF代替中值,来表征系统可靠性的设计要求[12].

为了使系统达到费用与性能之间的最佳平衡,就需要以最低的寿命周期费用使系统达到规定可靠性要求,对系统的可靠性和经济性进行综合权衡.开展预防性维修应该保证系统在每个预防性维修周期内具有一定的可靠度.设系统的最低可靠度要求为R0,在已知故障率函数的情况下,每个预防性维修周期内可靠度可以表示为

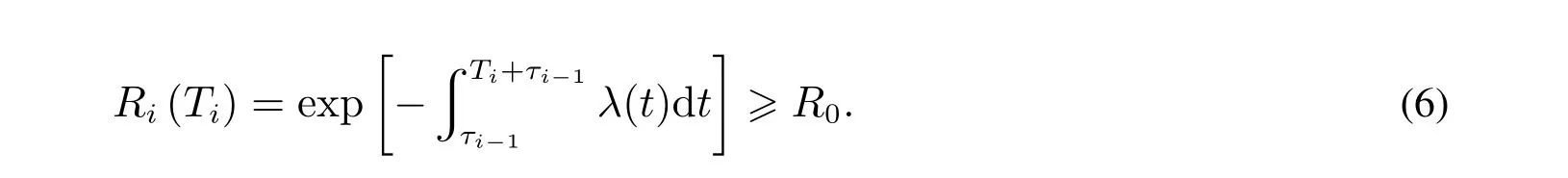
如果只考虑n个预防性维修周期内的可靠性,可能导致从最后一次预防性维修周期结束到T这段时间内系统运行可靠度很低.因此还要考虑从第n次预防性维修后到T时刻的系统可靠度

3 全寿命周期成本分析

从全寿命周期角度对系统的LCC进行分析,除了维修费用,设计费用和制造费用也需要纳入考虑.下面分别讨论系统的设计费用、制造费用和维修费用.

3.1 设计费用CD

目前的研究普遍认同随着系统可靠性的增加,系统的设计费用也随之增加.Huang[13]和Jin[4]在研究中提到设计费用随着可靠性呈指数级增长,他们在系统寿命服从指数分布和失效率为常数的条件下,提出了设计费用函数.

在系统寿命服从威布尔分布的条件下,故障率不再是常数,因此,用引入系统寿命中值的倒数,令h=1/MTTF来表征系统可靠性的设计值,对设计费用函数做如下改进.

设计费用CD可以表示为

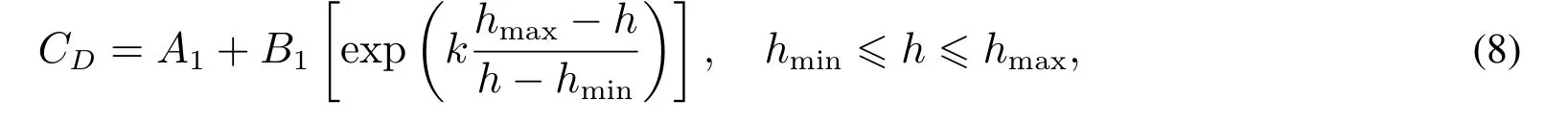
其中h表征系统的可靠性设计要求,hmax和hmin的值由ηmin和ηmax决定,分别表示系统能被接受的可靠性最低设计要求和能达到的最高可靠性设计要求.A1是hmax下的基本设计费用,B1表示为了提高系统可靠性所需的设计费用增量.常数k(k∈(0,1))表示在材料和资源约束下提高可靠性的难度系数.在给定基本设计费用A1的情况下,k和B1越大,表示在提高系统可靠性越困难,花费的设计成本也越高.

3.2 制造费用CM

系统可靠性的提高将对设计工艺、材料选择、制造精度提出更高的要求,因而制造费用会随着可靠性的改善持续增高.参考¨Oner[3]在故障率恒定的条件下提出了制造费用函数,对制造费用CM做如下改进

其中A2表示基本制造费用,B2表示在制造阶段为了提高系统可靠性需要增加的制造费用,υ表示提高系统可靠度的难度系数,取值为(0,1)之间的实数.从模型可看出,在给定A2的条件下,B2和υ越大,需要花费的制造费用越多.

3.3 维护费用CR

考虑系统在运行区间[0,T]内的维修的情况.预防性维修能够降低系统的故障修复费用,但进行预防性维修需要花费一定的时间和费用,过多的预防性维修活动会使总维修成本增加,造成“过维修”;而维修活动不足会使故障发生的频率增高,增加系统的故障维修成本,造成“欠维修”.因此,必须合理的规划预防性维修在特定时间区间内的次数以及开始时间等,使系统的总维修成本降到最小.维护费用主要由系统的故障小修费用和预防性维修费用构成.

1)故障小修费用

其中Cb为发生一次故障的小修费用,Fi为第i个预防性维修周期内的发生故障次数.

2)预防性维修费用

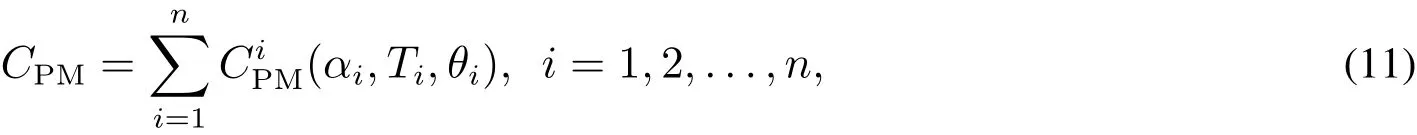
因此,维护费用CR可表示为

3.4 LCC优化模型

综上,全寿命周期成本π等于设计费用CD、制造费用CM、维护费用CR之和.由于系统在使用寿命周期内的可靠度不得低于设计要求的最低可靠度,所以全寿命周期成本的优化需要在可靠度的约束下进行.因此,以系统全寿命周期成本最小为目标函数,在系统可靠度要求下,建立以下模型

模型中的决策变量包括威布尔分布的形状参数m(m>1),尺度参数η(η>0),预防性维修次数n(n= 1,2,...),预防性维修周期Ti(Ti,i=1,2,...,n)以及预防性维修时间θi(θL<θi<θU),其中,θL和θU分别为进行预防性维修所需要的最短和最长预防性维修时间.约束条件1和2确保系统在预防性维修周期各阶段内的可靠度大于设计要求值.约束条件3保证维修时间和工作时间之和不超过系统的寿命周期.约束条件4限定了预防性维修时间的取值范围.由于模型涉及到整数规划和非线性规划的复杂性,需要通过编写一个优化算法求解.

为了说明预防性维修的必要性,式(15)考虑不进行预防性维修的系统全寿命周期成本,其中系统的维护费用仅包括小修费用,即

4 系统设计均衡区域的决策方法

从系统设计的角度来看,系统的可靠性指标体现了生产研制工作的可靠性设计水平和使用方对系统性能的要求.可靠性指标过高,将增加研制难度、周期和成本,甚至使研制工作失败.而可靠性指标过低,则影响系统使用效能,增加维护使用的工作量和费用.因此,综合来看,系统可靠性设计要求的确定,必须充分平衡上述两方面的影响,寻找既符合系统性能要求,经济性又最好的设计方案.

频繁的预防性维修,虽然可以降低系统LCC,但降低了系统可用性,因此,系统最优设计区间的确定不能仅根据LCC最小值确定,而应权衡系统LCC、可靠性水平和预防性维修次数,找到一个系统设计的均衡区域.

系统设计均衡区域的决策步骤如下:

步骤1对式(13)、(14)和式(15)优化求解.

优化后,可分别得到系统在进行预防性维修情况下的LCC和不进行预防性维修情况下的LCC.在不同可靠性水平下,可绘制出三条曲线:曲线I是在常规维修的条件下,即不考虑预防性维修时,系统在不同可靠性水平下的LCC曲线,是一条连续的曲线.曲线II是开展预防性维修后,在不同可靠性水平下,通过优化系统LCC和最优预防性维修次数得到的一组最优点连接而成的一条离散的曲线.两条曲线对应点的差值,表示开展预防性维修对系统LCC的减少带来的效用,即曲线III.

步骤2根据系统LCC函数,确定可靠性设计区间.

步骤3确定最优预防性维修次数.

在可靠性水平η∗下的最优预防性维修次数n∗的确定,就是将η∗代入式(13)和式(14).预防性维修次数在[Round(n∗)−1,Round(n∗)+1]的范围内都是合理的.

步骤4确定系统设计均衡区域.

结合曲线I和曲线II,依据步骤2和步骤3确定的可靠性设计值η的区间,就可确定系统设计的均衡区域.在这一区域内,系统LCC,系统可靠性设计水平η和预防性维修次数得到最优平衡.

当工艺水平得到改善,或成本函数发生变化时,利用上述提出系统设计均衡区域的决策思路和方法,可以重新得到系统新的均衡设计区域,将为系统的综合优化设计提供解决思路和有效的方法.

5 数值算例

以某大型装置的光学系统为例,验证上述构建的可靠度约束下系统全寿命周期成本优化模型的正确性.

该大型装置上使用的光学系统材料稀缺,加工工艺复杂,成本很高,极难获取,因而非常昂贵和珍贵,在高通量运行条件下,如果不加控制,激光诱发的损伤很快就会使元件报废,造成装置运行成本的急剧增加,极大地影响装置的效用.如果在光学元件没有出现灾难性损伤之前将元件换下,去除抛光杂质,对损伤区域进行维修,就能使元件循环使用,从而延长光学元件使用寿命、提高装置高效稳定运行能力[14].

形状参数m的取值通常是根据工程经验和历史数据来确定,如过去的故障数据及故障的失效机理等.参照文献[15],根据已有的工程经验和数据,考虑m=2时,对尺度参数η、全寿命周期成本和维修策略进行综合优化.假设每次预防性维修的役龄回退量相同,即αi=0.95,i=1,2,...,n.

表1和式(16)的参数取值参照现有工程数据给定,式(13)和(14)的求解在Lingo软件环境下实现.

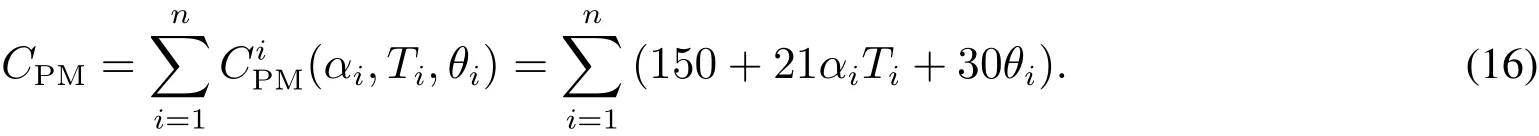
表1 相关参数Table 1 Relevant parameters

优化结果如表2所示.从表2可以看出,随着η的减小,预防性维修的次数增加.原因是在m给定的情况下,随着η的减小,相同时间段上的系统可靠度递减,因此,需要加大维修力度,使系统的可靠度满足要求.另外,以表2第4列为例:当η=134.7时,需要对系统进行4次预防性维修,系统全寿命周期成本为219 229元,各预防性维修周期的长度分别为63.6,60.5,57.7,55.2(单位h).从计算结果看出,由于等效役龄的影响,各预防性维修周期不再是等周期而是周期越来越短,这说明随着系统故障率的增加,需要对系统进行越来越频繁的预防性维修,这与工程实际情况相一致.θi的优化值为维修时间下限2.5h,即要求每次预防性维修活动尽可能用最短的时间恢复系统状态.

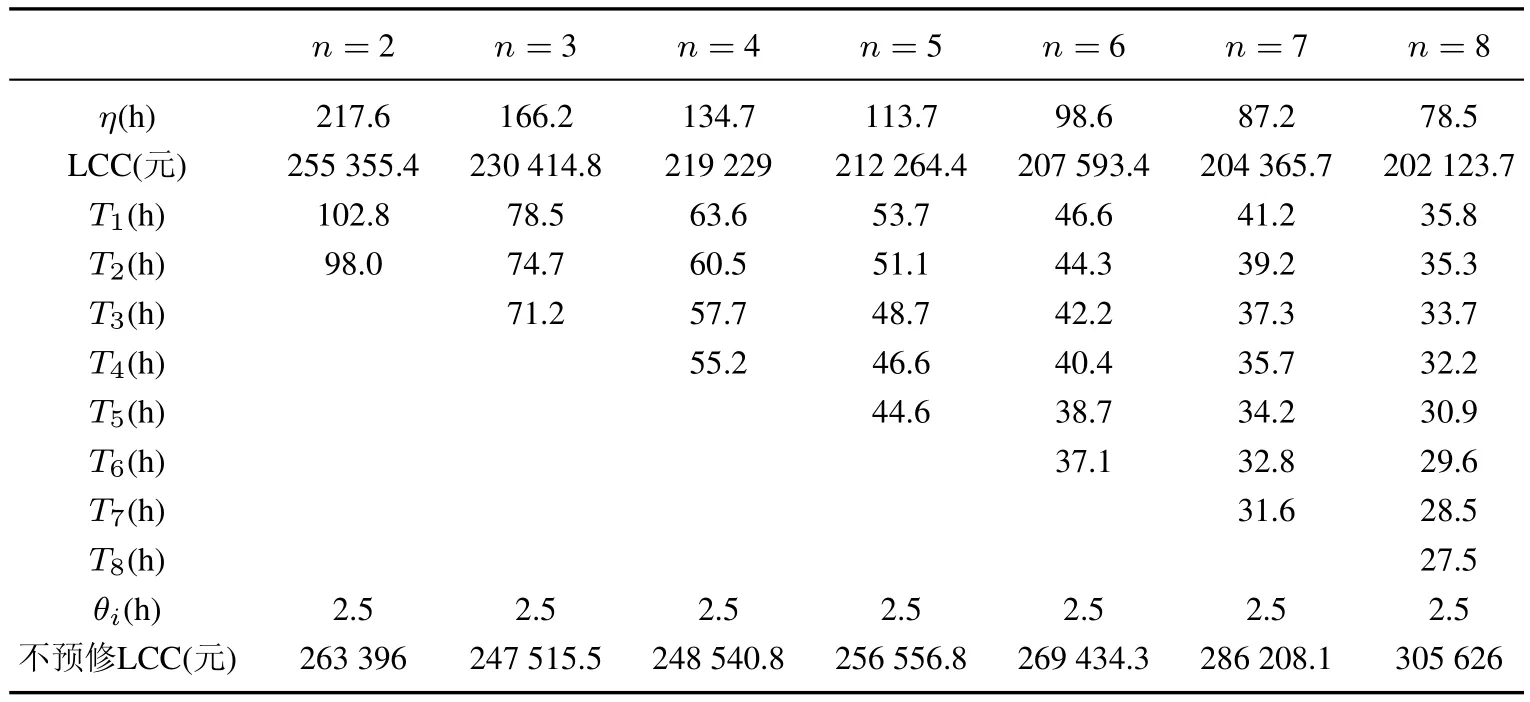
表2 优化结果Table 2 Optimized results

图1 最优LCC与η的关系Fig.1 Relationship between optimal LCC and η

进行预防性维修和不进行预防性维修的系统全寿命周期成本的比较如图1所示,在任何可靠度水平下,进行预防性维修的系统全寿命周期成本都要低于不进行预防性维修的系统全寿命周期成本,并且随着可靠度的降低,即η的减小,曲线I和曲线II的差值越来越大,即预防性维修的效用越来越明显.这是因为预防性维修降低了故障率,大大减小了系统的维修费用.进一步研究发现:

曲线I是系统在常规维修,即不考虑预防性维修的情况下的系统LCC值.曲线I呈抛物线状,是研制费用和维修费用共同作用的结果.随着η的增加,即随着系统可靠性的增加,相应的设计费用和制造费用大幅增加,而维护费用降低.在拐点之前,维修费用的降低多于设计费用和制造费用的增加.而在拐点之后,维修费用的减少已经不能消抵研制费用的快速增加,因此系统全寿命周期成本呈现上升趋势.曲线I验证了LCC曲线最低点的存在性.

曲线II由离散的点组成的,这些点表示在给定的可靠性水平下,寻找最优预防性维修策略后,优化的系统全寿命周期成本的最小值.曲线II位于曲线I之下,说明在系统寿命服从威布尔分布(m>1)的条件下,开展预防性维修后的优化LCC低于不开展预防性维修的LCC.曲线II也代表了开展预防性维修后,系统LCC的下限值,即系统LCC不会低于曲线II.曲线II随着可靠性水平的增加呈现递增趋势,说明在最优预防性维修策略下,随着η的增加,系统LCC增加的趋势不变.选取曲线II上的三个点A、B、C做具体分析:A点虽然LCC最低,但是需要进行频繁的预防性维修,影响了系统的可用性.C点可靠性的设计值高,所要求的工艺水平高,需要投入的总成本大,但开展预防性维修的效用值低.B点对应的η值虽然不高,但系统LCC和性能处于比较合理的位置,可以满足系统的正常使用.

曲线III是一条效用曲线,是曲线II与曲线I对应点的差值,表示在优化LCC条件下,开展预防性维修带来的成本减少效用.在给定的可靠性水平区间内,预防性维修的效用随可靠性水平的增加呈递减趋势.

此外,当m(m>1)取值不同时,上述LCC优化模型依然成立,采用系统设计均衡区域决策方法依然可以得到相应的系统设计均衡区域.例如,可利用该模型优化得到m=1.5时,η∈[142.6,170.0]以及n=4和n=5所对应的系统设计均衡区域;m=3时,η∈[130.0,170.3]以及n=2和n=3所对应的系统设计均衡区域.

6 结束语

LCC优化研究应充分体现全局性和系统性的思想.针对系统全寿命周期的各阶段费用及其关键影响因素的全局优化问题,上述构建可靠性约束下的LCC优化模型,将设计阶段的可靠性目标值与运维阶段的维修策略进行跨阶段的综合分析,找出不同维修策略下的可靠性设计水平与最优LCC的关系曲线,由此得到的效用曲线揭示了预防性维修的成本效用随可靠性水平的增加呈明显递减趋势.紧接着,提出的系统均衡设计区域决策方法,可以帮助设计师找出系统可靠性设计水平、维修策略和系统LCC的均衡区域.当技术的进步和工艺的不断改进时,虽然关键影响参数发生变化,但利用上述的优化模型和决策方法,设计师依然可以找到系统改进的新的均衡区域,因此,具有一定的工程应用价值.

[1]Benjamin S B.Design and Manage to Life Cycle Cost[M].Portland:M/A Press,1978:6.

[2]Yeung A A,Yoho K D,Arkes J.Estimates of unit cost reductions of the F-16 fghter as a result of U.S.arms export production[J]. Journal of Cost Analysis and Parametrics,2013,6(1):3–22.

[3]¨Oner K B,Kiesm¨uller G P,Houtum G J.Optimization of component reliability in the design phase of capital goods[J].European Journal of Operational Research,2010,205(3):615–624.

[4]Jin T,Wang P.Planning performance based contracts considering reliability and uncertain system usage[J].Journal of the Operational Research Society,2012,63(10):1467–1478.

[5]Lu K,Zhang Y,Suo M G.Study on the maintenance strategy of power equipment based on optimal LCC[C]//Power and Energy Engineering Conference,Wuhan:IEEE,2011:1–5.

[6]Waghmode L Y,Sahasrabudhe A D.Modelling maintenance and repair costs using stochastic point processes for life cycle costing of repairable systems[J].International Journal of Computer Integrated Manufacturing,2012,25(4):353–367.

[7]Smets L P,Houtum G J,Langerak F.Design for availability:A holistic approach to create value for manufacturers and customers of capital goods[J].Journal of Systems Science and Systems Engineering,2012,21(4):403–421.

[8]Barlow R,Hunter L.Optimum preventive maintenance policies[J].Operations Research,1960,8(1):90–100.

[9]程志君,杨 征,郭 波.基于PH分布近似的系统维修优化模型研究[J].系统工程学报,2010,25(1):137–144.

Cheng Zhijun,Yang Zheng,Guo Bo.Analysis of system optimal maintenance model with phase type approximation[J].Journal of Systems Engineering,2010,25(1):137–144.(in Chinese)

[10]韩帮军,范秀敏,马登哲.基于可靠度约束的预防性维修策略的优化研究[J].机械工程学报,2003,39(6):102–105.

Han Bangjun,Fan Xiumin,Ma Dengzhe.Research on the optimal preventive maintenance policy based on reliability constraints[J]. Chinese Journal of Mechanical Engineering,2003,39(6):102–105.(in Chinese)

[11]陈光宇,杨 东,张小民,等.激光装置片状放大器组件的氙灯可靠性分析[J].强激光与粒子束,2007,19(7):1125–1128.

Chen Guangyu,Yang Dong,Zhang Xiaomin,et al.Reliability analysis of Xe-f lashlamps of disk amplifer subsystems for laser facility[J].High Power Laser and Particle Beams,2007,19(7):1125–1128.(in Chinese)

[12]Ebeling C E.An Introduction to Reliability and Maintainability Engineering[M].Illinois:Waveland Press,2005:51.

[13]Huang H Z,Liu H J,Murthy D.Optimal reliability,warranty and price for new products[J].IIE Transactions,2007,39(8):819–827.

[14]彭志涛.强激光复杂光机组件光学元件激光损伤在线检测技术研究[D].绵阳:中国工程物理研究院,2011:4–6.

Peng Zhitao.Strong Laser Complex Opto-mechanical Components Laser-induced Damage Online Inspection Technology[D].Mianyang:China Academy of Engineering Physics,2011:4–6.(in Chinese)

[15]Grooteman F.A stochastic approach to determine lifetimes and inspection schemes for aircraft components[J].International Journal of Fatigue,2008,30(1):138–149.

Optimization modeling of system lifecycle costs under reliability constraints

Chen Guangyu,Zheng Shuyang,Feng Yi
(School of Management and Economics,University of Electronic Science and Technology of China, Chengdu 611731,China)

System design has some limitations if solely depending on lifecycle costs minimum or system reliability maximum.Under the condition that the life of a system follows Weibull distribution,preventive maintenance strategies,a design cost function,a manufacturing cost function and a repair cost function are presented, and then a lifecycle costs optimization model under reliability constraints is given.A decision method of equilibrium area for system design is put forward completely,which includes lifecycle costs,reliability design level and the times of preventive maintenance.An example analysis of optical systems of a large-scale facility is shown to demonstrate the applicability and effectiveness of our proposed model,and to provide solutions and methods for the decision process of system design of the equilibrium area.

system design;reliability;lifecycle costs;preventive maintenance;equilibrium area

TP273

A

1000−5781(2015)04−0 442−09

10.13383/j.cnki.jse.2015.04.00?

2013−08−20;

2014−06−19.

国家自然科学基金资助项目(71172095);科技部创新方法工作专项资助项目(2011IM020100).

陈光宇(1969—),男,四川雅安人,博士,副教授,硕士生导师,研究方向:系统可靠性工程,E-mail:chenguangyu@uestc.edu.cn;

郑舒扬(1989—),女,四川西昌人,硕士,通讯作者,研究方向:质量管理与可靠性工程,E-mail:zhengraul@163.com;

冯 毅(1970—),男,四川彭州人,博士,副教授,硕士生导师,研究方向:决策理论,供应链管理,E-mail:fengyi@uestc.edu. cn.