Diophantine方程x3+1=3Qy2的整数解

李润琪

（德宏师范高等专科学校数学系，云南　芒市　678400）

Diophantine方程x3+1=3Qy2的整数解

李润琪

（德宏师范高等专科学校数学系，云南芒市678400）

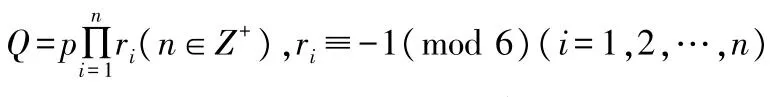
是一类基本而重要的Diophantine方程，其整数解已有不少人研究过.主要结论为：当（Q不含6k+1形素因子时主要结论见文献［1］；但当（Q含6k+1形素因子同时还含6k-1形素因子时，方程的求解较为困难，主要结论见文献［2-7］.本文主要对（Q含1个6k+1形素因子及至少含1个6k-1形素因子的情况进行讨论.

1　相关引理

引理1［8］设r≡5（mod 6）为奇素数，（x，y）为x2-3y2=1的整数解，则x0（mod r）.

引理2［9］设p是一个奇素数，则丢番图方程4x4-py2=1除开p=3，x=y=1和p=7，x=2，y=3外，无其他的正整数解.

引理3［9］设p是一个奇素数，则丢番图方程x4-py2=1除开p=5，x=3，y=4和p=29，x=99，y=1 820外，无其他的正整数解.

2　主要结论及证明

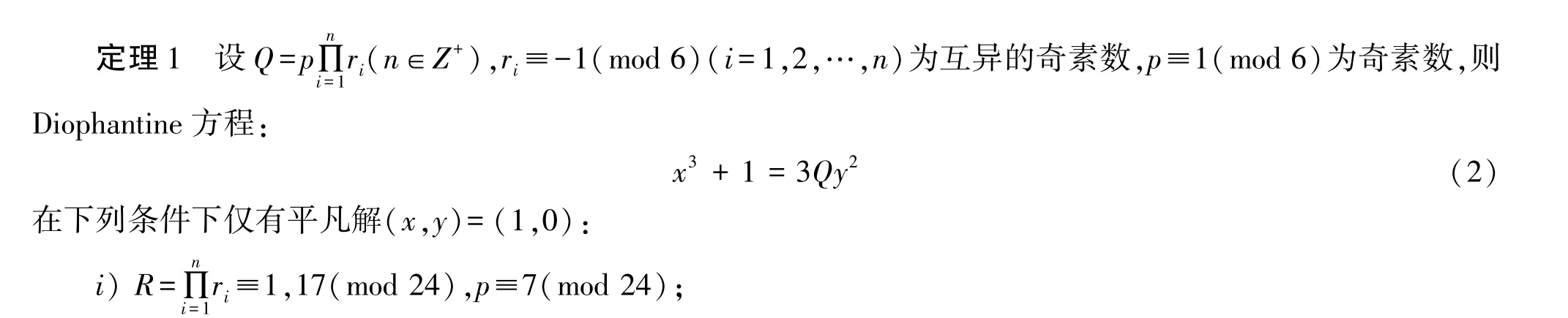
证明 设（x，y）是方程（2）的整数解，则gcd（x+1，x2-x+1）=3，x2-x+1≡0（mod 9）.又ri≡-1（mod 6）（1≤i≤s）是彼此不相同的素数，故x2-x+1≡0（mod ri）（1≤i≤s），则方程（2）可分解为以下两种情形：

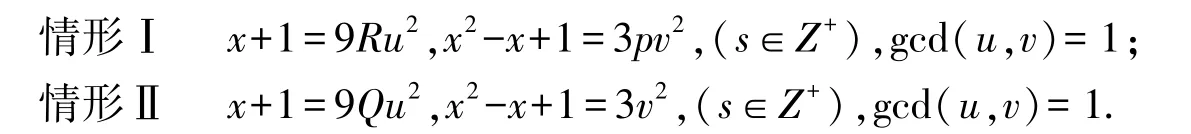
情形Ⅰ 由于u2≡0，1，4（mod 8），则由x+1=9Ru2得：x=9Ru2-1≡Ru2-1≡-1，R-1，4R-1（mod 8）；而由x2-x+1=3pv2及p≡1（mod 6）为奇素数知v为奇数，则v2≡1（mod 8），故3pv2≡3p（mod 8）.

由R≡1，17（mod 24）得：R≡1（mod 8），则x≡-1，R-1，4R-1≡-1，0，3（mod 8），则x2-x+1≡1，3，7（mod 8）；又由p≡7（mod 24），得：p≡7（mod 8），则3pv2≡3p≡≡5（mod 8），则有：1，3，7≡x2-x+1=3qv2≡5（mod 8），矛盾，故在条件（i）下情形Ⅰ不成立.

同理在（ii）条件下有：3，5，7≡x2-x+1=3qv2≡1（mod 8），矛盾；在条件（iii）、（iv）下有3，7≡x2-x+1= 3qv2≡1，5（mod 8），矛盾.故在条件（ii）（iii）（iv）下情形Ⅰ不成立.

综上有情形Ⅰ下方程（2）无整数解.

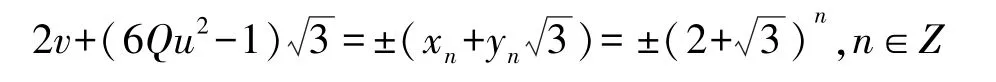
因此有：6Qu2-1=±yn（n∈Z），即有：6Qu2=±yn+1.又因为y-n=-yn，所以只需考虑下式：由式（4）得：yn≡-1（mod 6）.

容易验证下列各式成立：

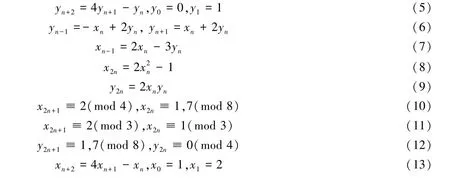
对递归序列（5）取模6，得周期为6的剩余类序列0，1，4，3，2，5，0，1，4，3，2，5，…，且仅当n≡-1（mod 6），有yn≡-1（mod 6），故（4）成立需n≡-1（mod 6），即n≡-1（mod 12）或n≡5（mod 12）.

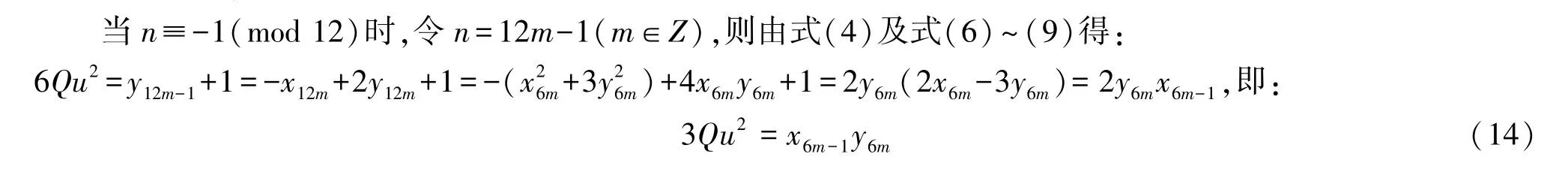
由式（7）及式（12）得：gcd（x6m-1，y6m）=gcd（2x6m-3y6m，y6m）=gcd（2x6m，y6m）=2.由式（11）得：x6m-1≡0（mod 3）.又因为ri≡-1（mod 6）（i=1，2，…，n）为互异的奇素数，则由引理1得：x6m-1≡0（mod ri）（i=1，2，…，n），则式（14）给出以下2种可能的分解：

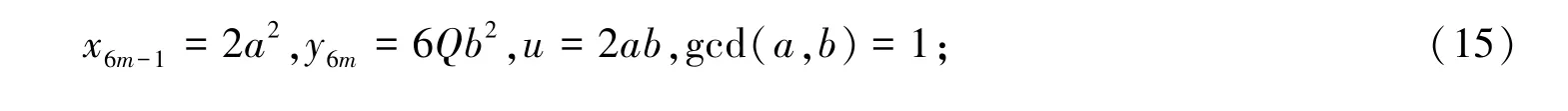
在条件（i）下，R≡1，17（mod 24），p≡7（mod 24），则p+R≡0（mod 8），则有4≡0（mod 8），矛盾，故条件（i）下（21）式不成立.

同理，在条件（ii）下有4≡0（mod 8）；在条件（iii）、（iv）下有4≡±2（mod 8），矛盾，故条件（ii）、（iii）、（iv）下式（21）均不成立.

综上有情形Ⅱ下方程（2）无整数解.

综上所述，定理1成立.

［1］柯召，孙琦.关于丢番图方程x3±1=3Dy2［J］.四川大学学报，1981，18（2）：1-5.

［2］曹玉书，郭庆俭.关于丢番图方程x3±1=3Dy2［J］.黑龙江大学自然科学学报，1989（4）：68-71.

［3］张淑静，杨雅琳，贾晓明.关于Diophantine方程x3±1=3pD1y2［J］.山西师范大学学报（自然科学版），2009，293（4）：31-33.

［4］杜先存，万飞，赵金娥.关于不定方程x3±1=1455y2的一个初等解法［J］.西南大学学报（自然科学版），2014（4）：43-46.

［5］杜先存，孙映成，万飞.关于丢番图方程x3±1=3·2αpD1y2［J］.数学的实践与认识，2014，44（6）：255-258.

［6］杜先存.关于丢番图方程x3±1=3qPy2的整数解［J］.郑州大学学报（理学版），2015，47（1）：38-41+45.

［7］普粉丽，张汝美，杨吉英.Diophantine方程x3+53=2pqy2的整数解［J］.湖北民族学院学报（自然科学版），2015，33（3）：264-265，270.

［8］万飞，杜先存.关于不定方程x3±1=2pDy2的整数解［J］.郑州大学学报（理学版），2015，47（1）：42-45.

［9］曹珍富.丢番图方程引论［M］.哈尔滨：哈尔滨工业大学出版社，2012：180，187.

责任编辑：时 凌

On Integer Solution of the Diophantine Equation x3+1=3Qy2

LI Runqi
（College of Mathematics，Dehong Normal College，Mangshi 678400，China）

Diophantine equation；integer solution；odd prime；recursive sequence；congruence；quadratic residue

O156.1

A

1008-8423（2015）04-0393-03DOI：10.13501/j.cnki.42-1569/n.2015.12.009

2015-10-31.

云南省教育厅科学研究项目（2014Y462）.

李润琪（1965-），男，讲师，主要从事初等数论及数学教育的研究.

解的性质、同余式、平方剩余、递归序列等证明了Diophantine方程x3+1=3Qy2仅有平凡解（x，y）=（-1，0）.关键词：Diophantine方程；整数解；奇素数；递归序列；同余；平方剩余