一个带有扰动因子的修正DL共轭梯度法

吴双江，杜学武

（重庆师范大学数学科学学院，重庆　401331）

一个带有扰动因子的修正DL共轭梯度法

吴双江，杜学武

（重庆师范大学数学科学学院，重庆401331）

本文研究无约束优化问题：

其中f：Rn→R为光滑函数.为解决无约束优化问题，可以采用非线性共轭梯度法，其通常有如下格式：

其中：gk=▽f（xk），αk＞0是通过某种线搜索获得搜索步长，βk是决定共轭梯度法类型的参数.

研究者对共轭梯度法做过许多研究，其中有6种早期经典的βk的取法如下：

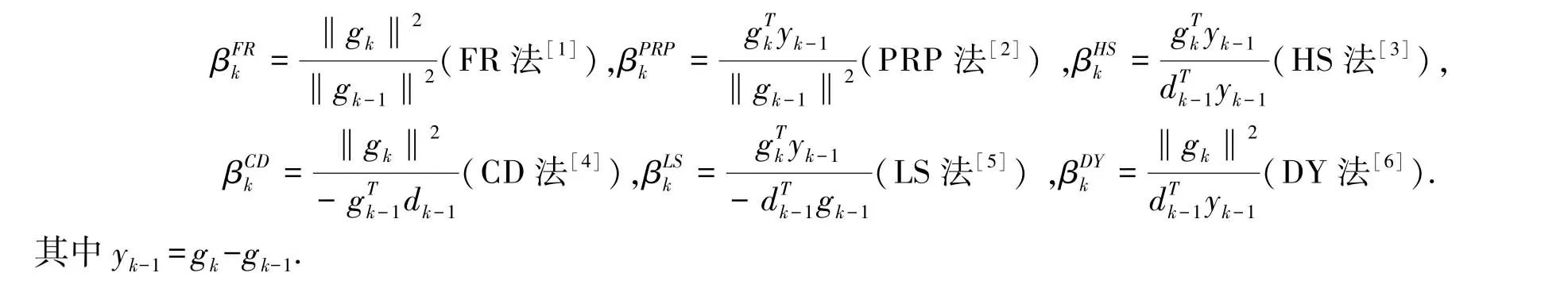
Yao等在文献［7］中提出修正HS法，记作MHS法，其βk具体形式如下：

Dai和Liao［8］提出DL共轭梯度法，βk的具体形式如下：

1　DMHSDL的理论性质

由假设A中②可知‖gk‖≤γ.

引理1［11］若假设A成立.对于迭代格式为式（2）～（3）的共轭梯度法，其中dk有充分下降性，αk是由强Wolfe线搜索获得的步长.如果：

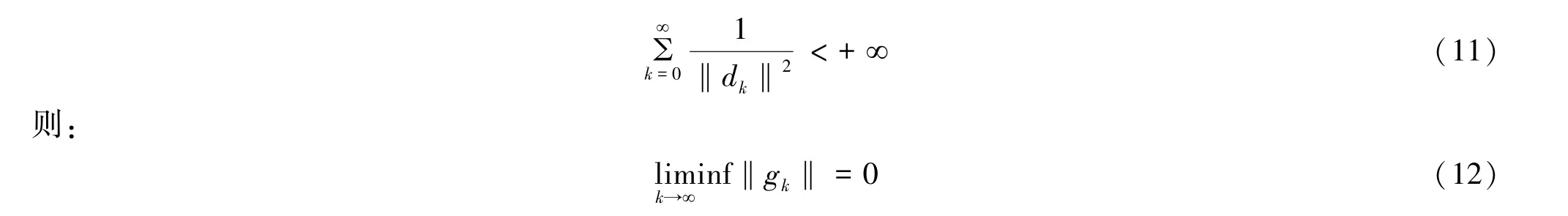
由式（3）和式（4）得：

其中θk是gk与gk与gk-1的夹角.证毕.

性质（*）［11］考虑迭代格式为式（2）～（3）的共轭梯度法，且假设：

如果存在两个常数b＞0和λ＞0，使得对任意k≥0满足：

则称共轭梯度法具有性质（*）.

引理3 若假设A成立.考虑迭代格式为式（2）～（3）的DMHSDL：

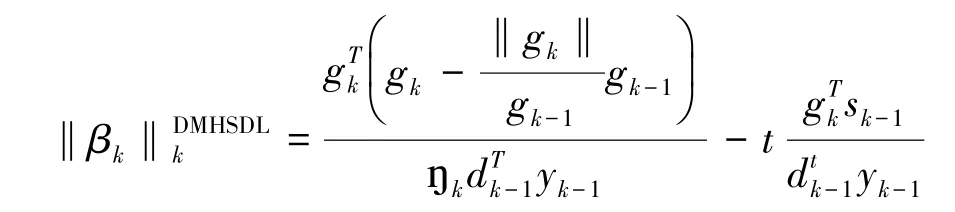
共轭梯度法.如果步长通过强Wolfe线搜索获得，则DMHSDL法具有性质（*）.

以下定理1、引理4和定理2的证明过程与文献［9］中的引理6、引理7和定理8相似，本文省略证明过程.

定理1 若假设A成立.通过强Wolfe线搜索获得步长的DMHSDL共轭梯度法，若存在常数γ＞0，使得：

2　数值试验

通过图1～4和表1可知，DMHSDL法在函数计算次数，梯度计算次数，迭代次数，时间上均好于其他几种方法.

表1　DL法，MHS法，MHSDL法，DMHSDL法的相对有效性Tab.1 The relative efficiency of DL，MHS，MHSDL and DMHSDL

图1　函数计算次数Fig.1 Performance profile on the number of function evaluation

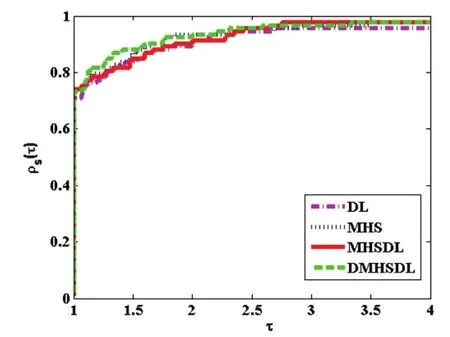
图2　梯度计算次数Fig.2 Performance profile on the number of gradient evaluation

图3　迭代次数Fig.3 Performance profile on the number of iteration evaluation

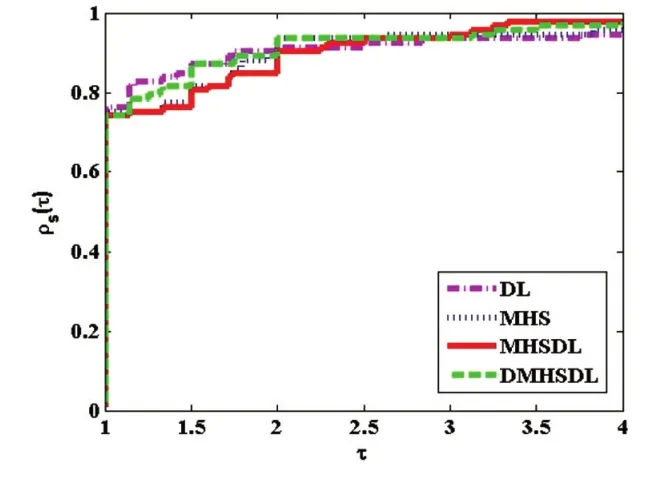
图4　CPU时间Fig.4 Performance profile on CPU time

［1］FLETCHER R，REEVES C M.Function minimization by conjugate gradients［J］.The Computer Journal，1964，7（2）：149-154.

［2］NOCEDAL J，WRIGHT S J.Numerical Optimization［M］.2ndedition.Springer：Springer Series in Operations Research and Financial Engineering，2006.

［3］HESTENES M R，STIEFEL E.Methods of conjugate gradients for solving linear systems［M］.Washington DC：Research of the National Bureau of Standards，1952.

［4］FLETCHER R.Practical Methods of Optimization［M］.2ndedition，John Wiley&Sons，1987.

［5］LIU Y，STOREY C.Efficient generalized conjugate gradient algorithms［J］.JOTA，1991，69（1）：129-152.

［6］DAI Y H，YUAN Y X.Anonlinear conjugate gradient with a strong global convergence property［J］.SIAM Journal on Optimization，1999，10（1）：177 -182.

［7］YAO S W，WEI Z X，HUANG H.A note about WYL's conjugate gradient method and its applications［J］.Applied Mathematics and Computation，2007，191（2）：381-388.

［8］DAI Y H，LIAO L Z.New conjugacy conditions and related nonlinear conjugate gradient methods［J］.Appl Math Optim，2001，43（1）：87-101.

［9］YAO S W，LU X W，WEI Z X.A conjugate gradient method with global convergence for largescale unconstrained optimization problems［J］.Journal of Applied Mathematics，2013，Article ID734454，9 pages.

［10］JIANG X Z，JIAN J B.Two modified nonlinear conjugate gradient methods with disturbance factors for unconstrained optimization［J］.Nonlinear Dynamics，2014，77（1/2）：387-397.

［11］GILBERT J C，NOCEDAL J.Global convergence properties of conjugate gradient methods for optimization［J］.SIAM Journal on Optimization，1992，1（2）：21-42.

［12］MORE J J，GARBOW B S，HILLSTROM K E.Testing unconstrained optimization software［J］.ACM Transactions on Mathematical Software（TOMS），1981，7（1）：17-41.

责任编辑：时 凌

A Modified DL Conjugate Gradient Method with Disturbance Factors

WU Shuangjiang，DU Xuewu
（School of Mathematics，Chongqing Normal University，Chongqing，401331，China）

conjugate gradient method；strong Wolfe line search；disturbance factors；global convergence

O224

A

1008-8423（2015）04-0375-04DOI：10.13501/j.cnki.42-1569/n.2015.12.005

2015-11-11.

国家自然科学基金项目（11171363）.

吴双江（1990-），男，硕士生，主要从事最优化理论与算法的研究.