一种考虑系统非理想特性的三相电压型PWM整流器控制参数设计方法

尹璐赵争鸣张凯任雪桂刘昊羽

（1.北京电力经济技术研究院北京100055 2.电力系统及发电设备安全控制和仿真国家重点实验室（清华大学）北京100084）

一种考虑系统非理想特性的三相电压型PWM整流器控制参数设计方法

尹璐1赵争鸣2张凯1任雪桂1刘昊羽1

（1.北京电力经济技术研究院北京100055 2.电力系统及发电设备安全控制和仿真国家重点实验室（清华大学）北京100084）

针对采用电网电压定向矢量控制的三相两电平电压型PWM整流器，按内模控制原理对其各调节器的参数进行设计。在此基础上，对控制延迟、采样误差、系统参数偏差和模型结构不准确等非理想因素对调节器控制性能的影响进行研究，提出考虑系统非理想特性条件下，基于内模控制原理的调节器控制带宽设计方法，并以一套由55 kW PWM整流器带55 kW PWM逆变器-异步电机负载组成的四象限双PWM变频调速系统为例，进行仿真和实验验证。

PWM整流器内模控制控制系统非理想特性并网控制

0　引言

三相电压型脉宽调制（Pulse Width Modulation，PWM）整流器因具有并网点功率因数可调、电网电流谐波小、能量可双向流动以及直流母线电压可控等优点，被广泛应用于电动机调速及新能源等领域［1，2］。特别是随着主动配电网的发展，PWM整流器作为可调负荷和分布式电源的主要并网拓扑形式，具有广阔的应用前景。

目前，PWM整流器的并网控制策略仍以基于电网电压定向的矢量控制（Voltage Oriented Control，VOC）为主。该控制策略采用基于电网电压矢量定向的同步旋转坐标系，实现了电网有功电流和无功电流的解耦控制。其物理意义明确，开关频率固定，具有良好的稳态性能［3］。针对该控制策略的电流内环和电压外环调节器存在多种设计方法，主要分为线性控制和非线性控制两类［4］。线性控制方法包括PID控制以及预测控制等，其控制结构简单、可靠性高；非线性控制包括反馈线性化、滞环比较以及模糊控制等，这些方法通常存在结构复杂及开关频率不固定等不足。目前，基于同步旋转坐标系的PID控制方法仍是这类调节器的主流设计方法。

在众多PID控制参数整定方法中，内模控制原理作为一种控制系统的设计理念，与常规的PID工程设计方法相比，具有整定参数少、物理意义明确、鲁棒性强等优点，在PI控制参数设计中具有显著优势［5，6］。基于内模控制方法整定的PID控制器仅有控制带宽一个参数，从而避免了反复实验试凑的过程［7］，提高了参数整定效率。

文献［8］针对过程控制中的PID参数与内模控制的关系进行了分析。文献［9］将内模控制方法引入异步电动机矢量控制系统，得到了各调节器的设计方法，但缺乏实验验证，并且未给出各调节器控制带宽的选取方法。文献［10，11］对内模控制在PWM整流器中的应用进行了研究，但也未给出带宽选取与系统性能的定量关系。

由于在实际控制中通常采用数字控制系统，同时在常规控制结构中会对系统数学模型进行化简，这些均导致控制系统设计时使用的数学模型与实际系统存在差异。而基于内模原理的PID调节器参数整定的控制效果与系统数学模型的准确度有很大关系，因此有必要对数字控制系统的非理想特性对控制效果产生的影响进行研究和补偿。

本文按照内模控制原理，对PWM整流器电压定向矢量控制中各PID调节器的控制参数进行了设计，并深入分析了离散控制系统中控制延迟、采样误差、系统参数偏差和模型结构不准确等非理想因素对PID调节器的控制性能产生的影响。在综合考虑系统稳态和动态性能的情况下，提出了一种考虑系统非理想特性的控制带宽选取方法。

1　考虑非理想特性的系统数学模型

三相三线制两电平电压型PWM整流器的主电路拓扑如图1所示。为了便于分析，电网等效为Y联结。图中，Lg为电网侧滤波电感，Rg为滤波电感中的等效电阻，Cdc为直流母线滤波电容，Rdc为直流母线的放电电阻，ea、eb、ec分别为电网相电压，ira、irb、irc分别为电网相电流，ura、urb、urc分别为整流桥输入端的等效相电压，udc为直流母线电压，irdc为由整流桥流入直流母线的直流电流，iCdc为流入母线电容的电流，iRdc为流入直流母线放电电阻的电流，iL为由直流母线流入负载的直流电流。系统电流和电压正方向的定义如图1所示。

图1　PWM整流器主电路拓扑Fig.1 The topology of a PWM Rectifier

对于三相三线制系统，由于系统不含零序分量，所以可将系统各变量通过Clarke变换和Park变换，变换至d-q坐标系中，得到PWM整流器的频域模型为

根据VOC控制理论，可得到PWM整流器的双闭环矢量控制结构，如图2所示。其中，ACR为电网电流调节器，AVR为母线电压调节器，D（s）为由于数字系统的PWM产生环节造成的一差拍控制延迟，*表示对应变量的设定值，Pref为整流桥的输入功率，PL为负荷侧的消耗功率，PCdc为直流母线电容和放电电阻上消耗的功率，为负载电流的前馈值。由于PWM重装载机制，在连续域中可近似采用一个1.5倍控制周期的惯性环节代替。假设系统控制周期为Ts，则

图2　PWM整流器闭环控制系统结构图Fig.2 The block diagram of control system

2　调节器设计

2.1电网电流调节器设计

根据先内环后外环的设计原则，首先设计电网电流内环调节器的控制参数。根据对角线内模控制器（Diagonalinternal Model Control，DIMC）的设计方法［12］，首先将交叉耦合项和电网电压视为外部扰动，在考虑控制延迟的情况下，PWM整流器的电流模型开环传递函数为

式中下标x表示d、q轴。设计电流内环的低通滤波器为

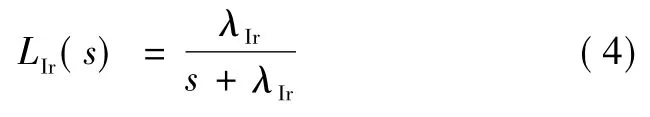
式中λIr为滤波器的截止频率，即电网电流调节器控制带宽。可得到电网电流调节器的开环传递函数为

式中上标^表示对应参数的估计值。可看到，按照内模控制原理，电流调节器被设计为一个典型的PID控制环节。当开关频率足够高时，微分项很小，可忽略，则调节器变为一个典型的PI调节器。

2.2母线电压调节器设计

在设计母线电压外环时，假设电网电流内环控制准确，即认为电流内环为一阶低通滤波器。因此，可得到由电流参考值到直流母线电压的系统开环传递函数为

从式（7）可看出，这是一个典型的非线性控制系统，其中urd和urq为电流调节器的输出，导致系统中含有输入量和输出量的平方项。为了设计线性控制系统，需要将式（7）近似线性化，而后再利用内模控制原理设计电压调节器。为此，对电压调节器作如下假设：

1）为了系统稳定，通过控制算法和母线电容的设计，母线电压的波动幅度较小，因此在计算由整流桥输入至直流母线的直流电流时，可假设母线电压保持额定值udcN不变。

2）在母线电压环的控制带宽较低的情况下，电压环控制中可认为电网电流已趋于稳定，因此不考虑电感中的能量变化，整流桥的输入功率就是电网的输出功率，所以将整流桥的输入电压替换为电网电压，即

3）为了尽量减小系统损耗，直流母线的放电电阻通常会选择较大的值，因此该一阶惯性环节近似为积分环节。

根据上述线性化方法，可得到线性化后的系统开环传递函数为

设计母线电压外环的低通滤波器为

式中λV为母线电压调节器控制带宽。根据内模控制原理，可得到母线电压调节器的开环传递函数为

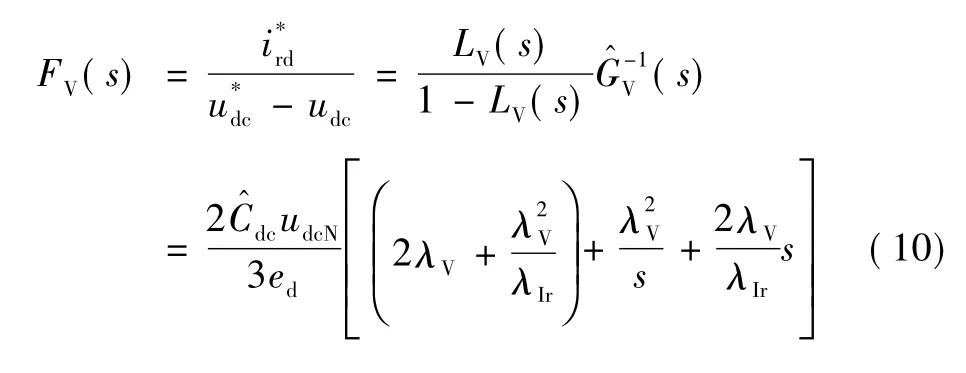
可看到，母线电压调节器被设计为典型的PID调节器。由于在调节器设计时认为电网电流的调节速度远大于母线电压的调节速度，因此在控制带宽设计时需满足λIr≫λV，即调节器微分项近似为0，可简化为PI调节器。

3　考虑系统非理想特性的PID调节器控制带宽选取方法

以一套由55 kW PWM整流器带55 kW PWM逆变器-异步电动机负载组成的四象限变频调速系统为例，说明PWM整流器控制系统中各调节器控制带宽的选取方法。实验系统主电路结构如图3所示，异步电动机额定功率为55 kW，由6RA70控制的直流发电机作为其负载。异步电动机采用基于转子磁链定向的矢量控制，各调节器均采用常规的PI控制器。当异步电动机在额定负载条件下，转速指令由1 200 r/min阶跃至1 500 r/min时，电动机动态响应的实验波形如图4所示。

图3　四象限变频调速实验系统主电路结构图Fig.3 Configuration of a PWM rectifier-inverter experimental system

图4　异步电动机转速阶跃响应实验波形Fig.4 Experiment results of themotor speed step response

由于本文仅验证所提出的并网整流器控制参数设计方法，因此此处仅列出了PWM整流器的主电路参数，如表1所示。

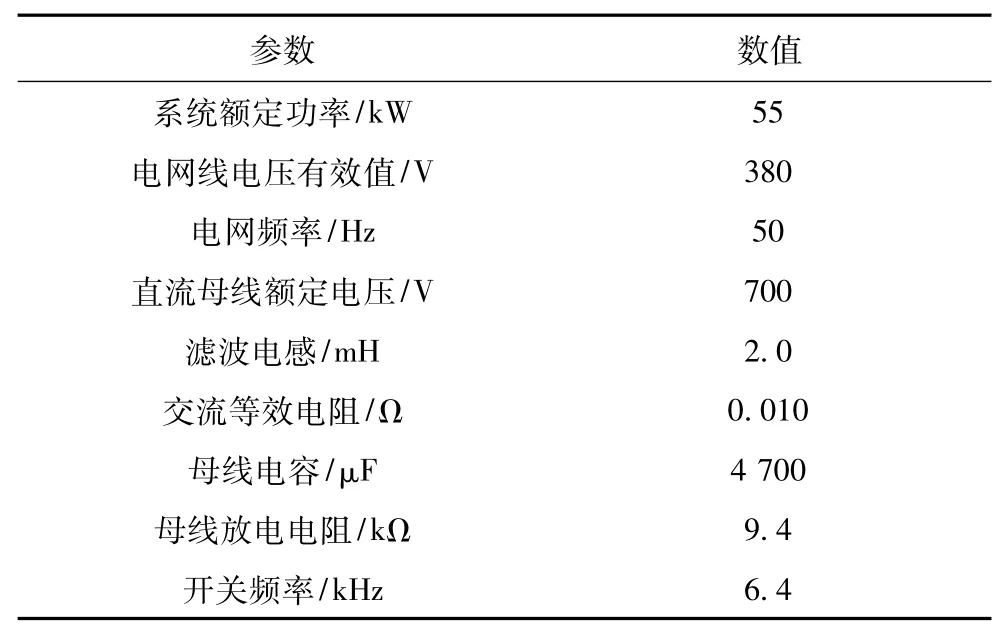
表1　PWM整流器主电路参数Tab.1 The parameters of the PWM rectifier

3.1电网电流调节器

根据内模控制原理，在理想条件下，系统电流环的闭环传递函数为低通滤波器LIr（s），因此控制带宽取值越大，系统动态响应效果越好。但在实际控制系统中，微分环节的存在会使系统对采样误差非常敏感，因此为了保证良好的稳态效果，通常采用在微分环节中加入一个一阶惯性环节的不完全微分算法以改善系统的抗干扰性能，或忽略微分项。同时，在离散控制系统中微分环节由后向差分实现，即使采用完全微分也无法精确实现调节器的传递函数。所以，为了减小系统延迟和系统参数误差等对控制效果的影响，调节器控制带宽的选择不能过大，需要控制在一个合理范围内。

根据控制方程和系统数学模型可得到电网电流内环的闭环传递函数为

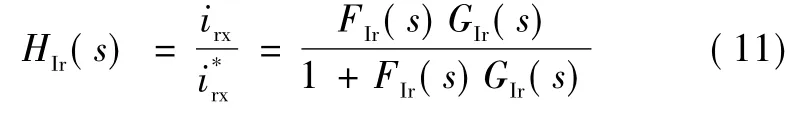
在开关频率为6.4 kHz时，控制带宽由100 Hz增加至1 000 Hz，忽略调节器的微分项，电网电流相对于其参考值的频率响应特性如图5所示。当控制带宽大于400 Hz后，系统闭环幅频特性曲线存在大于0的区域，这意味着此时系统对阶跃响应存在超调。当开关频率降至3.2 kHz，在其他条件相同的情况下，电网电流相对于其参考值的频率响应特性如图6所示。可以看到，随着开关频率的降低，系统控制延迟增加，相同控制带宽下系统超调更加明显。为了抑制控制延迟对系统超调的影响，当开关频率为6.4 kHz时，电网电流调节器控制带宽应设置在400 Hz左右；当开关频率为3.2 kHz时，应设置在200 Hz左右。

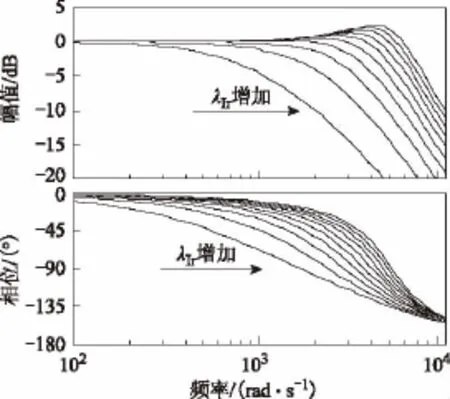
图5　开关频率6.4 kHz条件下电网电流相对于其参考值的频率响应特性Fig.5 Bode plot ofunder 6.4 kHz switching frequency

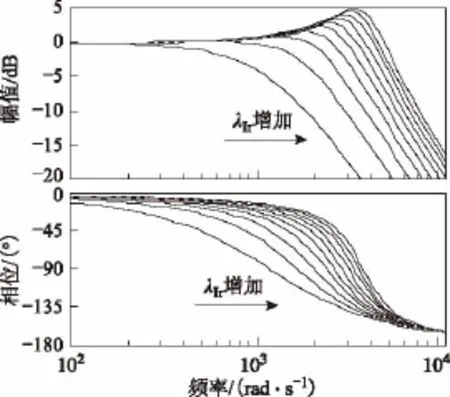
图6　开关频率3.2 kHz条件下电网电流相对于其参考值的频率响应特性Fig.6 Bode plot ofunder 3.2 kHz switching frequency

而对于交叉解耦项，同样由于控制延迟的影响，即使参数准确，交叉解耦项在动态过程中也不能完全消除d、q轴之间的耦合，其耦合关系为

为了保证系统良好的解耦效果，电流环的控制带宽应小于式（12）的转折频率，即

当开关频率为6.4 kHz时，控制带宽应小于4 267 rad/s，即679 Hz。

当开关频率为6.4 kHz时，该55 kW系统在不同控制带宽下，电网电流d轴分量的动态响应仿真波形如图7所示。由图7a和图7b可看出，由于内模控制中带入了系统模型，所以实际滤波电感参数的变化对控制效果影响不大。但当控制带宽过高时（如图7d中的控制带宽为600 Hz），由于控制延迟的影响，电流超调明显增大。当控制带宽较低时（如图7c中的控制带宽为300 Hz），电流的动态响应速度变慢，超调明显减小。当开关频率为3.2 kHz时，在不同控制带宽下，电网电流d轴分量的动态响应仿真波形如图8所示。与理论分析相同，由于控制延迟的增加，此时如果控制带宽仍设计为400 Hz，则会出现严重超调。

图7　开关频率6.4 kHz条件下电流环阶跃响应仿真波形Fig.7 The dynamic performance of current loop under 6.4 kHz switching frequency

图8　开关频率3.2 kHz条件下电流环阶跃响应仿真波形Fig.8 The dynamic performance of current loop under 3.2 kHz switching frequency

当开关频率为6.4 kHz，电网d轴电流参考值阶跃时，按照仿真设定电流调节器参数，系统的实验波形如图9所示。与仿真结果基本相同，在400 Hz时电流波形存在一定的超调。针对2 mH滤波电感，仿真和实验中电流的上升时间如表2所示。根据控制理论，对于一阶系统，当输入为阶跃指令时，系统响应由10%上升至90%的时间τ和控制带宽λ的关系为

可看出，仿真结果、理论值和实验结果基本相同。

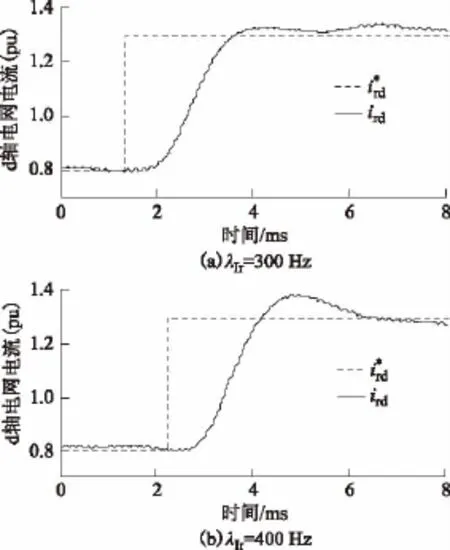
图9　开关频率6.4 kHz条件下电流环阶跃响应实验波形Fig.9 Experimental results of the dynamic performance of current loop under 6.4 kHz switching frequency

表2　电流环阶跃响应仿真与实验比较Tab.2 Simulation and experimental resultscomparisonof the dynamic performanceof current loop

3.2母线电压调节器

在选择母线电压调节器控制带宽时，需要考虑电网电流变化过程中电感储能的变化。为了将系统线性化，采用小信号分析的方法可得到母线电压外环的闭环传递函数为

式中：Ird为系统稳定工作点的电网电流，A；和分别为母线电压实际值和参考值的变化量，V。

同样以本节的实验系统为例，开关频率为6.4 kHz，当母线电压调节器控制带宽由10 Hz增加至50 Hz时，不同稳定工作点的情况下母线电压相对于其参考值的闭环频率响应特性分别如图10和图11所示。

当稳态输入功率为0时，相当于不考虑电感中能量变化带来的影响，如图10所示，此时系统最大增益基本相同，仅是最大增益出现的频率随控制带宽增加而增加。同时系统稳定裕量随带宽增加而减小，这是由于在电压外环调节器设计时假设系统电流内环已进入稳态，而母线电压的控制带宽越小，该假设越准确。取系统实际的外环转折频率为内环的1/5，在开关频率为6.4 kHz时，母线电压调节器的控制带宽可取为20～30 Hz。

图10　稳态输入功率为0条件下母线电压相对于其参考值的频率响应特性Fig.10 Bode plot ofwhen the steady-state input power is 0

当稳态输入功率为额定值时，此时电感中能量变化带来的影响最严重，由于此时的系统模型与内模设计时相比已发生了变化，因此系统闭环频率特性也与设计的低通滤波器不尽相同。从图11中可看到，当控制带宽大于30 Hz后，闭环系统转折频率处的增益明显增加，这意味着电压环的超调增加，同时会放大该频段采样误差对系统的影响。

图11　稳态输入功率为额定值条件下母线电压相对于其参考值的频率响应特性Fig.11 Bode plot ofunder rated steady-state input power

当异步电动机以额定负载转矩、额定转速运行时，电网电流调节器控制带宽为400 Hz，母线电压调节器控制带宽与电网电流稳态THD的实验关系如表3所示。可看到，由于采样误差和系统模型理想化的影响，当母线电压环控制带宽较高时，会引起电流谐波含量上升。在同样条件下，母线电压参考值由650 V阶跃至700 V，电压的理论上升时间和实际上升时间如表4所示，由于实际系统的限制，母线电压的动态跟随性能不能随带宽升高而无限提升。因此综合考虑系统的动态和稳态性能，可选择电压调节器控制带宽为20 Hz。

表3　母线电压调节器控制带宽与电流谐波畸变率对比Tab.3 The relationship between the bandwidth of DC-link voltage loop and current THD

表4　母线电压外环阶跃响应理论与实验值比较Tab.4 The comparison between the theoretical and actualdynamic performance of DC-link voltage loop

在上述调节器参数的控制下，55 kW电动机在额定负载条件下，转速指令由1 200 r/min阶跃至1 500 r/min时，电网电流和母线电压的动态响应实验波形如图12所示。

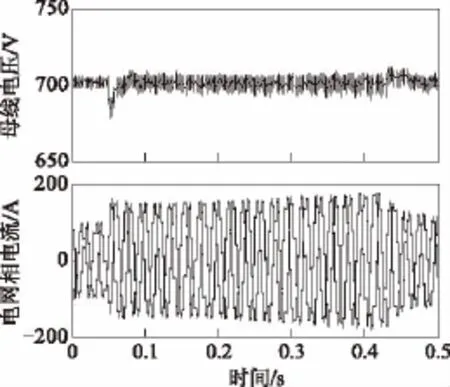
图12　PWM整流器负载突变的动态响应实验波形Fig.12 Experimental results with the load torque steps

4　结论

本文在分析了PWM整流器数学模型的基础上，根据内模控制原理，设计了矢量控制结构中各PID调节器。重点研究了控制延迟、采样误差、系统参数偏差和模型结构不准确等非理想因素对系统控制性能产生的影响，提出了一种考虑系统非理想特性的调节器控制带宽设计方法，减小了系统非理想特性对控制性能的不良影响，在保证系统稳态性能的前提下最大限度的提升了动态响应速度。

［1］周秋燕，刘文胜，曹志斌.双PWM变频技术的应用研究［J］.变频器世界，2008（7）：52-54.

Zhou Qiuyan，Liu Wensheng，Cao Zhibin.Applied research on dual-PWM frequency conversion technology［J］.TheWorld of Inverters，2008（7）：52-54.

［2］李时杰.基于Back-to-Back变流技术的调速系统的研究［D］.北京：中国科学院研究生院（电工研究所），2006.

［3］张崇巍，张兴.PWM整流器及其控制［M］.北京：机械工业出版社，2003.

［4］Kazmierkowski M P，Malesani L.Current control techniques for three-phase voltage-source PWM converters：a survey［J］.IEEE Transactions on Industrial Electronics，1998，45（5）：691-703.

［5］宋文祥，尹赟.一种基于内模控制的三相电压型PWM整流器控制方法［J］.电工技术学报，2012，27（12）：94-101.

Song Wenxiang，Yin Yun.A control strategy of threephase PWM rectifier based on internalmodel control［J］. Transactions of China Electrotechnical Society，2012，27（12）：94-101.

［6］Rivera D E，Morari M，Skogestad S.Internal model control 4 PID controller design［J］.Industrial& Engineering Chemistry Process Design and Development，1986，25（1）：252-265.

［7］胡斯登.考虑非理想特性与特定工况的变频调速系统控制策略研究［D］.北京：清华大学，2011.

［8］卓越.基于内模原理的PID控制器参数整定的研究［D］.保定：华北电力大学，2007.

［9］周渊深.感应电动机交-交变频调速系统内模控制研究［D］.徐州：中国矿业大学，2004.

［10］全吉男，王聪，韩春艳.三相电压型PWM整流器的内模解耦控制［J］.电力电子技术，2007，41（7）：14-16.

Quan Ji'nan，Wang Cong，Han Chunyan.Internal decoupling control of three-phase voltage source PWM rectifier［J］.Power Electronics，2007，41（7）：14-16.

［11］邓富金，蔡旭.基于内模控制的双闭环PWM整流器［J］.电力电子技术，2008，42（6）：60-62.

Deng Fujin，Cai Xu.Double closed-loop PWM rectifier based on internalmodel control［J］.Power Electronics，2008，42（6）：60-62.

［12］Harnefors L，Nee H P.Model-based current control of AC machines using the internal model control method［J］.IEEE Transactions onIndustry Applications，1998，34（1）：133-141.

A Regulator Design M ethod for Three-phase Voltage-source PWM Rectifiers Considering the Non-ideal Characters of the Control System

Yin Lu1Zhao Zhengming2Zhang Kai1Ren Xuegui1Liu Haoyu1
（1.Beijing Electric Power Economic Research Institute Beijing 100055 China 2.State Key Lab of Control and Simulation of Power Systems and Generation Equipments Tsinghua University Beijing 100084 China）

This paper presents a regulator designmethod based on the internalmodel control for three-phase voltage-source PWM rectifiers，which are controlled by voltage oriented vector control.Meanwhile，this paper analyzes the influence of the non-ideal characteristics of the control system，including control delay，sampling error，system parameter mismatch，model structure in accurateness，etc.，on the performance of regulators. Then，a bandwidth design method considering the non-ideal characteristics of the system is proposed，which is verified by simulation and experiment in a 55 kW induction motor driven by a 55 kW rectifier-inverter fourquadrant double PWM frequency control system.

PWM rectifier，internalmodel control，the non-ideal characters of the control system，gridconnected control

TM461.5

尹璐男，1985年生，博士，工程师，研究方向为主动配电网规划与技术应用。（通信作者）

赵争鸣男，1959年生，博士，教授，研究方向为太阳能光伏发电、电力电子与电机集成系统。

国家高技术研究发展（863）计划（2014AA051901）资助项目。

2015-05-29改稿日期2015-10-10