基于模型预测控制的主动配电网电压控制

蔡宇林今宋永华舒彬张凯

（1.清华大学电机与应用电子技术系北京100084 2.北京电力技术经济研究院北京100055）

基于模型预测控制的主动配电网电压控制

蔡宇1林今1宋永华1舒彬2张凯2

（1.清华大学电机与应用电子技术系北京100084 2.北京电力技术经济研究院北京100055）

为解决主动配电网中分布式可再生能源和储能系统造成的电压波动影响，基于模型预测控制理论提出了主动配电网电压调节控制策略，充分利用主动配电网中分布式电源、储能系统和有载调压变压器，实现采用最小控制成本的控制方案进行电压控制。该控制方案基于模型预测控制，采用多步滚动优化，使得电压控制过程更为灵活平滑，控制模型求解采用二次规划。通过IEEE 33节点辐射状配电网系统算例分析，证明了所提电压控制策略的可行性和有效性。

主动配电网有载调压变压器模型预测控制电压控制二次规划

0　引言

近年来随着新能源和分布式发电技术的快速发展，分布式电源（Distribued Generation，DG）在主动配电网中的发展既带来了机遇，又带来了新的挑战［1，2］。由于分布式新能源的间歇性使主动配电网中时常出现过电压或低电压等问题，使得配电网用电用户电能质量受到负面影响［3］。

针对配电网电压控制问题，通常通过调节有载调压变压器（On-Load Tap Changer，OLTC）或投切电容器实现电压控制。但这些控制措施具有离散性，不能灵活地进行电压调节，若增加如SVG等调压措施又给配电网带来较大的经济负担。为此，本文基于主动配电网现有的分布式电源、储能、OLTC等，提出一种适合主动配电网的电压控制策略，既可灵活地实现电压调节，又能减少配电网工程建设的投资。

文献［4］对DG接入配电网后对电压的影响进行了全面分析，研究表明，所接入DG的类型、出力、位置及负荷水平等均对配电网系统电压水平有直接影响。文献［5］定性分析了基于线性负荷指数不同负荷模型的辐射状配电网电压稳定问题。文献［6］从电网电压降落角度研究了光伏发电接入配电网后的电压问题，并提出了包括电抗器补偿、线路中央控制与逆变器无功控制结合和安装储能装置等控制措施。文献［7］使用储能装置实现配电网电压调节，提出一种基于多种低碳技术的电压控制策略。文献［8］提出一种以控制变量变化最小为目标的日内调节DG出力的控制策略，并保证电压满足日前给定运行范围。

随着模型预测控制理论的发展，基于多步滚动优化模型的预测控制在许多工程问题中得到应用。模型预测控制作为研究新能源接入后系统潮流控制的一种研究方法得到广泛重视。文献［9-11］将模型预测控制理论应用于电力系统，研究了输电网长期电压稳定控制问题。文献［12］基于模型预测控制理论对含DG配电网的能量管理系统进行了研究。

本文针对主动配电网的电压问题，基于模型预测控制理论提出了一种电压控制策略。该控制策略充分利用主动配电网中分布式电源、有载调压变压器和储能系统，以实现灵活有效的电压控制。该控制策略以控制成本最小为目标，考虑储能使用寿命，保证母线电压运行在正常运行范围内。

1　模型预测控制理论基础

模型预测控制（Model Predictive Control，MPC）能有效克服系统的非线性、时变性、不确定性以及干扰等因素的影响，被广泛应用于工业过程中［13］。虽然模型预测控制具有各种不同的算法实现形式，但其共同特征是包含了预测模型、滚动优化和反馈校正三大重要部分。其核心思想是：在k时刻，考虑系统未来有限时段状态，使用当前时刻测量值和预测模型，通过具有控制约束和目标函数的极小化，得到当前和未来有限时段的最优控制。而在k+1时刻，利用k时刻控制后的测量数据重复这一优化过程。模型预测控制的原理如图1所示。图1中，横轴为时间区域，其中Np表示预测步长，Nc表示控制步长，且Np≥Nc，纵轴为系统输出。时刻t=k将时间区域分为两部分，左边为过去实际输入输出，右边为将来预测输入输出。在k时刻，基于当前测量信息优化求得Nc步控制变量Δu=［Δu（k|k），Δu（k+1|k），…，Δu（k+Nc-1|k）］，以满足预测时域k+Np的目标状态。但每个时刻只执行Nc个控制变量中的第一个控制变量Δu（k|k）。在k+1时刻重复上述过程。

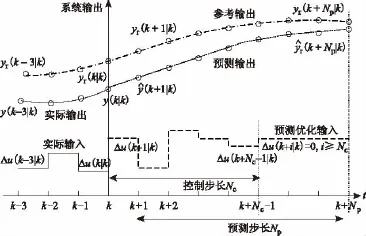
图1　模型预测控制原理图Fig.1 Principle ofmodel predictive control

模型预测控制能够直接考虑控制过程的状态、输入和输出变量的约束条件，将其表示出来，控制器的设计直接体现被控过程的动态［14］。同时，模型预测控制将控制问题转换为优化问题求解，考虑控制对象未来的行为。对于预测模型建模，不需要深入了解过程内部的机理，不要求建立精细的预测模型，更关注实际中预测模型的效果。

2　基于模型预测的电压控制模型

本文将模型预测控制理论应用于主动配电网电压控制中，提出了一种基于模型预测控制的主动配电网电压控制策略。提出的电压控制策略通过调节主动配电网中分布式电源出力（Pg，Qg）、储能系统充放电（Ps，Qs）、有载调压变压器分接头档位（Vtap），以确保所监控的主动配电网母线电压运行在正常运行范围内。在k时刻控制变量为：Δu（k）=式中Δu（k）=u（k+1）-u（k）。控制目标为保证电压处于正常运行范围的控制成本最小，基于模型预测控制的电压控制策略模型为二次规划问题，如下［15］

式中i=0，1，…，Nc-1。

式中i=1，…，Np。

2.1电压控制目标函数

本文所提电压控制策略的控制目标是保证主动配电网母线电压运行在安全性和经济性允许的电压运行范围内。当母线电压运行在不允许的状态时，电压控制器优化得到控制成本最小的控制策略，使母线电压调整到允许的运行范围内。

在电压控制策略中，将电压的运行状态分为正常运行、不理想运行和紧急运行3个状态，根据配电网中电压所处的不同状态，采取成本不同的控制措施。①当母线电压处于正常运行状态时，无需采取任何控制措施；②当母线电压处于不理想运行状态时，通过调节控制成本较低的DG的无功出力、储能充放电和有载调压变压器分接头控制母线电压；③当母线电压处于紧急运行状态，通过调节包括控制成本较高DG的有功出力和其他所有可调控元件进行电压控制，直到电压回到不理想运行状态。

目标函数表示为

式中：Pgp、Pgq、Ptap、Psp、Psq分别为通过调节分布式电源有功和无功的控制成本、有载调压变压器分接头的控制成本、储能有功和无功的控制成本，且假设控制成本大小满足Pgp＞Ptap=Pgq=Psq=Psp；ng、nLTC、ns分别为可参与电压控制的分布式电源数量、有载调压变压器数量和储能数量；ΔPg，k、ΔQg，k、ΔVtap，k、ΔPs，k、ΔQs，k分别为第k个分布式电源有功出力和无功出力的调节量、有载调压变压器分接头的变化、储能有功和无功的调节量。

2.2预测模型

储能状态的预测模型如式（7）所示，考虑储能使用最佳寿命条件下的储能充电状态，要求储能充电状态满足约束式（6）。电压的预测模型如式（5）所示，本文采用系统的灵敏度模型作为电压控制预测模型。灵敏度矩阵∂V/∂u分别包含母线电压对功率注入（DG或储能）的灵敏度和母线电压对变压器分接头变动的灵敏度。由于灵敏度矩阵的更新依赖于配电网的运行状态（如重载运行、轻载运行），不要求频繁更新矩阵信息，可采用离线潮流计算得到灵敏度矩阵建立电压控制预测模型。

2.2.1母线电压对功率注入的灵敏度

母线电压对注入功率的灵敏度值可以由雅克比矩阵的逆求得，雅克比矩阵由离线潮流计算求得。该灵敏度矩阵包含母线电压对DG功率注入变化和母线电压对储能有功无功充放电变化。具体求取过程如下，采用牛顿法进行潮流计算得到式（9）。

式中雅克比矩阵为

式（9）等号左右乘以雅克比矩阵的逆可得

2.2.2母线电压对变压器分接头变动的灵敏度

母线电压对变压器分接头变动的灵敏度可以通过改变有载调压变压器一个分接头档位导致监控的母线电压变化值近似计算得到

式中：Vi为监控母线i的电压，（pu）；ΔVi为由于改变OLTC的一个分接头档位引起监控母线电压Vi的波动大小，（pu）；ΔVd为由于改变OLTC的一个分接头档位引起的OLTC端母线电压的波动大小，（pu）。

通过改变OLTC的分接头档位，连续计算两次离线潮流即可得到。

2.3约束条件

2.3.1控制变量的约束

1）分布式发电电源

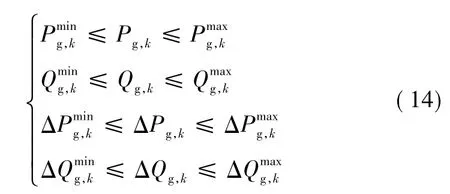
3）有载调压变压器

为简化模型求解的复杂性，将有载调压变压器档位作为连续变量进行控制求解，对于求解结果ΔVtap，k处理为

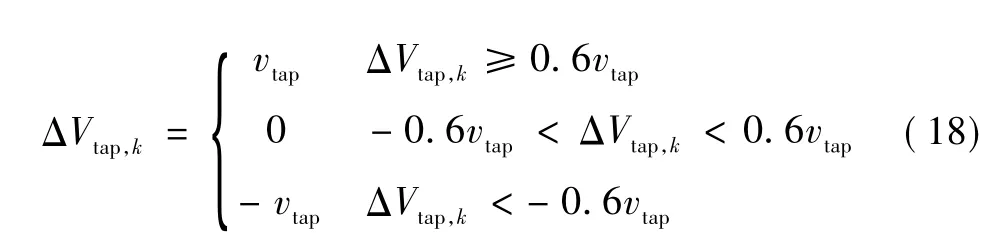
2.3.2约束处理

1）预测步长内渐进缩紧约束

如果控制器在每一步控制步都严格执行电压正常运行范围约束，控制器可能采取较大的控制变量或不必要的措施；如果只在控制步长的最后一步执行电压正常运行范围约束，可能导致控制过程缓慢。为此，本文对预测时域内电压正常运行范围约束进行了渐进缩紧的处理，使得电压约束逐渐缩紧，并在最后控制步长严格满足电压正常运行的约束，如图2所示。渐进缩紧的电压约束为

式中：i=1，…，Np；ρ为调整电压约束值的调节参数。

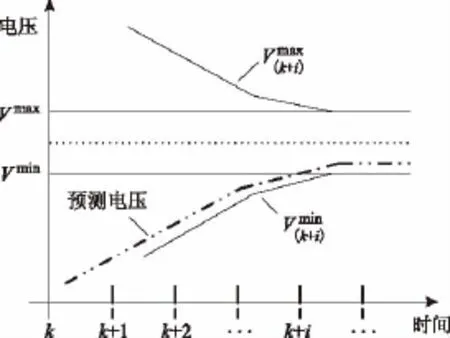
图2　渐进紧缩的电压约束条件Fig.2 Progressive tightening of voltage limits

2）增加松弛变量

在某些特殊情况下，控制手段无法将电压控制到电压正常运行范围内，即优化问题无可行解。这种情况通常由于电压约束或储能充放电状态约束太紧，使得无法将电压控制在正常运行范围内，或者分布式电源或储能出力达到上限或下限值等。实际中，控制器得不到可行解是一种非常严重的情况，尤其处于紧急运行状态时。为此，将约束中式（4）和式（6）增加松弛变量变为式（21）和式（22），以保证能控制器能得到可行解，尽可能将电压控制到接近正常运行范围。注意，仅在控制器由于约束过紧而无法得到可行解时才增加松弛变量。

相应目标函数应修正为

式中：ε=［ε1，ε2，ε3，ε4］T；S为松弛变量惩罚因子。

3　算例仿真

3.1算例系统

在11 kV IEEE 33辐射状配电网系统改进的基础上进行了仿真计算，如图3所示。该系统含有10台DFIG风电机组、2个有载调压变压器和1个储能装置，它们在系统中的位置如表1所示。风电机组的容量为5 MV·A，爬坡能力为0.5 MW。有载调压变压器设定参考电压值范围为［0.85，1.15］（pu），每一档位大小为0.013（pu），初始电压参考值为Vtap=1.000（pu），每次动作只能调节一个档位。储能容量为0.5 MW·h，储能充电状态SOC范围为［20%，80%］，逆变器充放电功率限制为0.002 MW，储能充放电效率为95%。

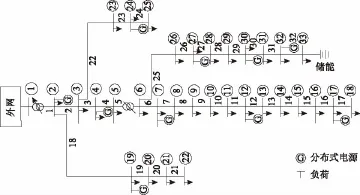
图3　改进的IEEE 33辐射状配电网接线图Fig.3 IEEE 33 radial distribution network topology

表1　DG、OLTC和储能在主动配电网中的位置Tab.1 The locations of DG，OLTCs and storages in IEEE 33 radial distribution network

针对OLTC提出了检测控制策略，即连续时间Ttest均检测到控制策略要求执行同样档位调节操作，则实际下发OLTC一次动作指令，且OLTC需要时间TLTC才能完成动作，算例中取Ttest=5 s，TLTC=10 s。系统母线电压正常运行范围为［0.96，1.02］（pu），不理想运行范围为［0.90，0.96）（pu）和（1.02，1.04］（pu），紧急运行范围为V＜0.90（pu）和V＞1.04（pu）。预测步长和控制步长为Np=Nc=3，调节参数为ρ=5。

3.2仿真结果

1）通过DG无功出力、储能充放电和OLTC调节配电网电压。

（1）配电网中负荷需求大，DG出力小，出现低电压。假设每处风电机组有功出力为2 MW，储能初始状态SOC=60%。配电网中典型母线电压大小如图4所示，通过DG无功出力、储能放电和OLTC档位调节，所有母线电压最终均控制运行在正常运行范围［0.96，1.02］（pu）。

图4　配电网母线电压大小Fig.4 Bus voltages in the active distribution network

由于配电网系统中母线低电压时处于不理想运行状态，所以采用成本较低的控制措施，不采用控制成本较高的DG有功出力进行调节。如图5所示，DG有功出力保持不变，DG无功出力增加，以提高母线电压。图6为有载调压变压器动作和储能充放电状态。OLTC1和OLTC2分别同时下调分接头一档，改变OLTC参考电压，储能通过放电实现配电网电压调节。

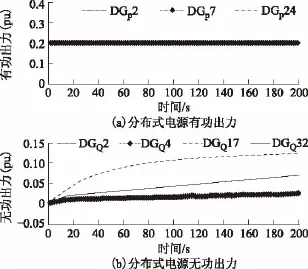
图5　分布式电源有功和无功出力Fig.5 Active and reactive power outputs of DGs

图6　有载调压变压器电压设置和储能控制状态Fig.6 Voltage set-point of OLTCs and storage control

（2）配电网中负荷需求小，DG出力大，出现过电压。假设每处风电机组有功出力4.5 MW，储能初始状态SOC=60%。配电网中典型母线电压大小如图7所示，通过DG无功出力和储能充电调节，所有母线电压最终均平滑地控制运行在正常运行范围［0.96，1.02］（pu）。

图7　配电网母线电压大小Fig.7 Bus voltages in the active distribution network

由于配电网系统中母线过电压时处于不理想运行状态，所以采用成本较低的控制措施，不采用控制成本较高的DG有功出力进行调节。如图8所示，DG有功出力仍保持不变，DG无功出力为负，表示DG进相运行，以降低母线电压。图9为OLTC电压值档位设置和储能充放电状态。OLTC1和OLTC2无需动作，储能通过充电实现配电网电压调节。

2）通过DG有功和无功出力、储能充放电和OLTC调节配电网电压。

在k=5 s时，外网故障导致外网戴维南等值电压升高0.08（pu）。每处风电机组有功出力为3 MW，储能初始状态SOC=60%。配电网母线电压如图10所示，通过DG有功和无功出力、OLTC及储能调节，母线电压最终均控制运行在正常运行范围。

图8　分布式电源有功和无功出力Fig.8 Active and reactive power outputs of DGs

图9　有载调压变压器电压设置和储能控制状态Fig.9 Voltage set-point of OLTCs and storage control

图10　配电网母线电压大小Fig.10 Bus voltages in the active distribution network

k=5 s后，系统电压处于紧急运行状态，故采用所有可控措施进行控制。如图11所示，DG有功出力减小，大部分DG无功出力为负，以降低母线电压。母线32所接DG无功出力增加是因为控制器预测该处母线电压过低，提前采取控制措施。OLTC1和OLTC2的协调动作设置的参考电压值以及储能放电状态如图12所示。

图11　分布式电源有功和无功出力Fig.11 Active and reactive power outputs of DGs

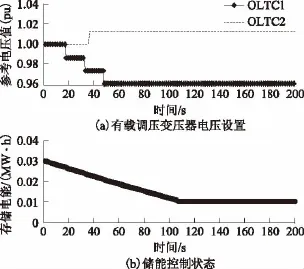
图12　有载调压变压器电压设置和储能控制状态Fig.12 Voltage set-point of OLTCs and storage control

4　结论

本文针对配电网电压波动问题，基于模型预测控制提出了一种主动配电网电压控制策略。该策略利用灵敏度矩阵建立了配电网电压和储能充放电状态的预测模型，基于多步滚动优化平滑地实现了配电网母线电压调节。控制策略中采用预测步长内逐渐缩紧和增加松弛变量处理约束条件，避免了无可行解情况的出现。通过算例分析，证明了该控制器能对配网中低电压、过电压和外网故障引起的电压问题进行有效调节。

［1］余贻鑫.新形势下的智能配电网［J］.电网与清洁能源，2009，25（7）：1-3.

Yu Yixin.Intelligent distribution network in the new situation［J］.Power System&Clean Energy，2009，25（7）：1-3.

［2］王守相，王成山.现代配电系统分析［M］.北京：高等教育出版社，2007.

［3］孔丽.含分布式电源的主动配电网电压特性的研究［D］.北京：北京交通大学，2012.

［4］陈芳，王玮，徐丽杰，等.分布式电源接入对配电网电压变化的分析［J］.电力系统及其自动化学报，2012，24（4）：145-149.

Chen Fang，Wang Wei，Xu Lijie，et al.Analyzing the voltage variation of distribution network including distributed generation［J］.Proceedings of the CSUEPSA，2012，24（4）：145-149.

［5］伍利，姚李孝，古婷婷.基于线性负荷指数不同负荷模型的辐射型配电网电压稳定性分析［J］.电力系统保护与控制，2011，39（13）：8-13.

Wu Li，Yao Lixiao，Gu Tingting.Radial distribution system voltage stability analysis by different load models based on linear load index［J］.Power System Protection and Control，2011，39（13）：8-13.

［6］许晓艳，黄越辉，刘纯，等.分布式光伏发电对配电网电压的影响及电压越限的解决方案［J］.电网技术，2010，34（10）：140-146.

Xu Xiaoyan，Huang Yuehui，Liu Chun，et al. Influence of distributed photovoltaic generation on voltage in distribution network and solution of voltage beyond limits［J］.Power System Technology，2010，34（10）：140-146.

［7］Wang Pengfei，Liang D H，Yi Jialiang，et al. Integrating electrical energy storage into coordinated voltage control schemes for distribution networks［J］. IEEE Transactions on Smart Grid，2014，5（2）：1018-1032.

［8］Borghetti A，Bosetti M，Grillo S，et al.Short term scheduling and control of active distribution systems with high penetration of renewable resources［J］.IEEE Systems Journal，2010，4（3）：313-322.

［9］黄义隆，谢敏，刘明波.基于修正轨迹灵敏度的模型预测长期电压稳定控制［J］.电力系统自动化，2012，36（3）：28-33.

Huang Yilong，Xie Min，Liu Mingbo.Model predictive control for long-term voltage stability based on correctedtrajectory sensitivities［J］.Automation of Electric Power Systems，2012，36（3）：28-33.

［10］王爽，刘明波，胡泊，等.基于Radau排列的非线性模型预测紧急电压控制器［J］.电工技术学报，2012，27（2）：243-249.

Wang Shuang，Liu Mingbo，Hu Bo，et al.Design of nonlinear model predictive emergency voltage controller using Radau collocation［J］.Transactions of China Electrotechnical Society，2012，27（2）：243-249.

［11］王爽，谢敏，刘明波.可行性恢复算法求解模型预测长期电压稳定控制问题［J］.电工技术学报，2012，27（9）：62-69.

Wang Shuang，Xie Min，Liu Mingbo.Feasibility restoration algorithm for solving model predictive longterm voltage stability control［J］.Transactions of China Electrotechnical Society，2012，27（9）：62-69.

［12］FalahiM，Lotfifard S，EhsaniM，et al.Dynamicmodel predictive-based energy management of DG integrated distribution systems［J］.IEEE Transactions on Power System，2013，28（4）：2217-2226.

［13］席裕庚.预测控制［M］.2版.北京：国防工业出版，2013.

［14］刘向杰，孔小兵.电力工业复杂系统模型预测控制—现状与发展［J］.中国电机工程学报，2013，33（5）：79-85.

Liu Xiangjie，Kong Xiaobing.Present situation and prospect ofmodel predictive control application in complex power industrial process［J］.Proceedings of CSEE，2013，33（5）：79-85.

［15］Valverde G，Cutsem T V.Model predictive control of voltages in active distribution networks［J］.IEEE Transactions on Smart Grid，2013，4（4）：2152-2161.

Voltage Control Strategy in Active Distribution Network Based on M odel Predictive Control

Cai Yu1Lin Jin1Song Yonghua1Shu Bin2Zhang Kai2
（1.Department of Electrical Engineering Tsinghua University Beijing 100084 China 2.Beijing Electric Power Economic Research Institute Beijing 100055 China）

In this paper，a model predictive control（MPC）-based voltage control strategy has been proposed to correct the voltage problems caused by renewable energy sources and storages in active distribution networks.The controller takes full use of distributed generations（DGs），storages，and on-load tap changers（OLTCs）to limit the voltages within the nominal operation region at the lowest cost.And a multi-step optimization is used to smooth the control process.This voltage control scheme leads to a quadratic programming problem which can be solved easily.Results obtained from simulation and comparative analysis on IEEE 33 node radial distribution network demonstrate the feasibility and effectiveness.

Active distribution network，on-load tap changer（OLTC），model predictive control（MPC），voltage control，quadratic programming

TM712

蔡宇女，1989年生，博士研究生，研究方向为模型预测控制、新能源接入和电压控制。（通信作者）

林今男，1985年生，博士，讲师，研究方向为主动配电网和风电控制。

国家高技术研究发展（863）计划（2014AA 051901）和国家自然科学基金（51207077、51261130472）资助项目。

2015-05-30改稿日期2015-08-19