线性调频脉冲串信号及其检测性能分析

岳　雷

（1.昆明船舶设备研究试验中心，云南 昆明，650000；2.西北工业大学 航海学院，陕西 西安，710072）

线性调频脉冲串信号及其检测性能分析

岳雷1，2

（1.昆明船舶设备研究试验中心，云南 昆明，650000；2.西北工业大学 航海学院，陕西 西安，710072）

针对主动声呐的混响抑制问题，研究了线性调频脉冲串（PTLFM）信号的时域频谱特性及模糊度函数特性，提出了采取宽带对称三角状调频形式PTLFM信号提高速度副瓣处的混响抑制性能的方法，根据梳状谱信号设计要求完成了PTLFM波形设计及PTLFM实测数据在复杂背景下不同运动速度的目标检测。理论分析、仿真结果及实测数据处理结果表明：对于静止或运动目标来说，锯齿状调频形式PTLFM信号的混响抑制性能优于对称三角状调频形式PTLFM信号；对于运动速度为其模糊度函数速度副瓣最大值的目标来说，对称三角状调频形式

线性调频脉冲串（PTLFM）；模糊度函数；混响抑制；波形设计；速度副瓣

0　引言

混响抑制一直是声呐和雷达领域的研究难点，目前主动声呐混响抑制技术研究主要集中在波形设计和处理算法两方面。已有文献表明［1-4］：采取波形分集技术的脉冲串信号，具有频谱梳状化、多普勒敏感、高速度-距离分辨力、模糊度函数呈钉板形特性，有着优良的抗混响性能。宽带平坦谱信号由于目标回波谱的频移通常比发射信号带宽小得多，使得目标回波的谱很难和混响的谱分开，导致检测性能很难提高；单频信号虽然有较好的速度分辨力，但当目标静止或运动产生的多普勒较小时，其频谱很难脱离混响带；宽带梳状谱信号由于其模糊度函数呈现钉板型，通过选取合适的波形参数既可以获得抗高多普勒混响的能力，也可以获得抗低多普勒混响的能力。由文献［1］和［2］可知，线性调频脉冲串（pulse trains of linear frequency-modulated，PTLFM）信号是一种典型的宽带多普勒敏感信号，具有频率调制、脉冲分裂等特点［3-4］，但是文献［3］并未研究PTLFM信号的频谱及模糊度函数特性。

假使目标运动使得混响的贡献主要来自信号模糊度函数的速度副瓣时，那么降低速度副瓣的电平是提高PTLFM信号混响抑制性能的有效途径。文献［5］虽然只从窄带情况下分析了对称三角PTLFM信号的模糊度函数，但是它提供了一种降低PTLFM信号速度副瓣的思路，即采用正负调频结合的脉冲串信号，使得其模糊度函数在原点附近的主瓣与主瓣叠加，旁瓣相互削弱或保持不变，主副瓣比得以提高，从而提高混响背景下速度副瓣处运动目标的检测性能。

文中首先研究了PTLFM信号的时域频谱特性及模糊度函数特性，分析了采取正弦平方包络对于PTLFM信号频谱、模糊度函数及抗混响性能的影响，并提出采取宽带对称三角调频形式的PTLFM信号以提高信号的混响抑制性能，同时根据抗混响波形要求设计PTLFM信号参数，最后根据实测数据完成混响背景下PTLFM信号检测，得出相应结论。

1　线性调频脉冲串（PTLFM）信号分析

1.1模糊度函数定义

模糊度函数是信号分析及波形设计的有力工具。波形抗混响能力的好坏，可以通过对发射信号模糊度函数的分析来获得，宽带回波信号的模糊函数和模糊度函数［3，6-7］分别定义为

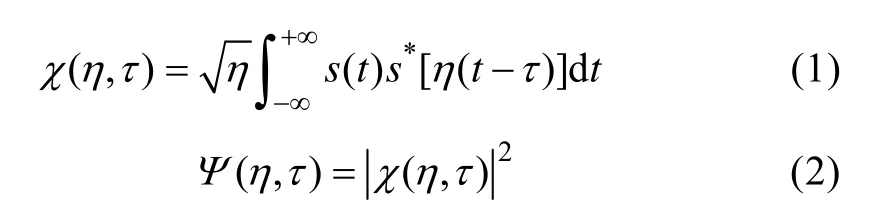
信号的模糊度函数描述了信号的时频域联合分布特性，可表征主动声呐系统匹配滤波处理的效果，信号对于目标的探测能力可以由模糊度图上的主瓣宽度得到，而旁瓣的高度决定了此信号对于多目标或者在混响限制条件下的探测能力。通过对比不同发射信号的模糊度图，可以得到其在混响条件下接收端的匹配滤波效果［7-8］。

1.2PTLFM信号时域频谱分析

PTLFM信号的表达式为

式中：A（n）为包络；p（t）为线性调频子脉冲。包络分为矩形包络和正弦平方包络，线性调频子脉冲又分为锯齿状调频形式和对称三角状调频形式。其中正调频或负调频形式为锯齿状调频形式，正负（负正）调频形式为对称三角状调频形式。

首先从频谱角度分析矩形包络和正弦平方包络，说明其优势所在。

图1是矩形包络和正弦平方包络PTLFM信号频谱图。为比较矩形包络和正弦平方包络PTLFM信号的频谱差异，这里取对数坐标。可以看出，相对于矩形包络而言，正弦平方包络PTLFM信号频谱的旁瓣级降低了20 dB；正弦平方包络PTLFM信号频谱的梳齿间隔和矩形包络PTLFM信号频谱的梳齿间隔一致，而前者的梳齿宽度比后者的梳齿宽度大一倍。

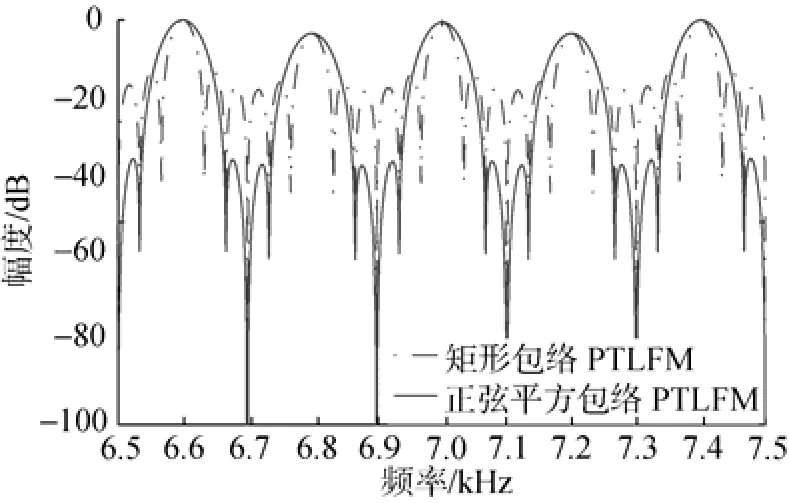
图1　矩形包络和正弦平方包络线性调频脉冲串（PTLFM）信号频谱图Fig.1　Frequency spectrum of the rectangular envelope and sine squared envelope pulse trains of linear frequency-modulated（PTLFM）signal

对于PTLFM信号来说，正弦平方包络降低了谱的旁瓣级，使得运动目标频谱和混响频谱在梳齿间隔处的重叠部分减小，从而减小测速模糊和提高波形的抗混响性能，然而这是以降低发射能量和减小速度分辨力为代价的。

相比较矩形包络而言，正弦平方包络PTLFM信号的混响抑制性能更好，因此下面重点分析正弦平方包络PTLFM信号。为描述方便，以ptlfm_saw表示锯齿状调频形式PTLFM信号，以ptlfm_syt表示对称三角状调频形式PTLFM信号。

ptlfm_saw信号时域表达式为

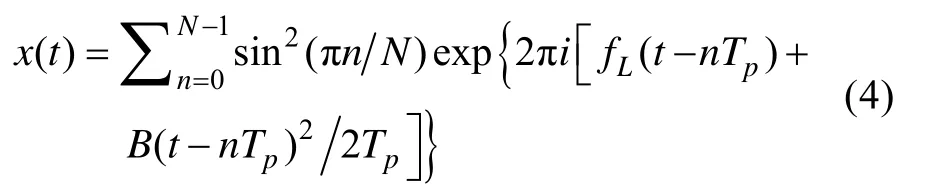
ptlfm_syt信号时域表达式为

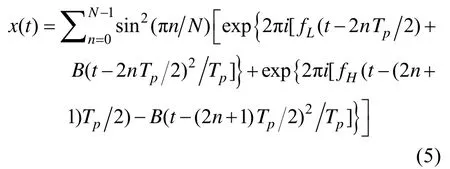
式中：fL是起始频率；B是带宽；Tp是子脉冲持续时间；N是子脉冲个数。

如图2和图3分别为ptlfm_saw和ptlfm_syt信号时域频谱图，此处参数选取：信号频段6～8 kHz，信号持续时间30 ms，子脉冲个数6。相同之处为其时域包络呈现正弦平方状、频谱梳状化；区别为对称三角调频形式的频谱不如锯齿调频形式的频谱平坦，这是由于对称三角调频形式的相干作用引起的。

图2　锯齿状调频形式PTFM（ptlfm_saw）信号时域频谱图Fig.2　Spectrum of the sawtooth PTFM（ptlfm_saw）signal　in time domain and frequency domain

对称三角调频形式的相干导致PTLFM信号频谱不再如锯齿调频形式PTLFM信号频谱那么平坦，这将会影响其模糊度函数特性及抗混响性能。1.3节将分析其模糊度函数特性及抗混响性能，指出对称三角调频形式PTLFM信号的优势。

图3　对称三角状调频形式PTLFM（ptlfm_syt）信号时域频谱图Fig.3　Spectrum of the symmetrical triangular PTLFM（ptlfm_syt）signal　in time domain and frequency domain

1.3PTLFM信号模糊度函数分析

将式（4）带入式（2），得

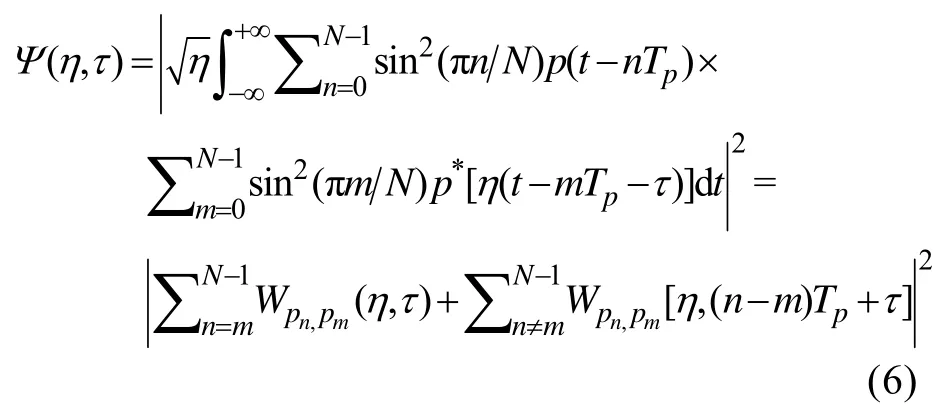
从式（6）可以看出，PTLFM信号的模糊度函数由自相关项和交叉项组成。

由模糊度函数的傅里叶变换性质可知

即信号的模糊度函数可以在频域上实现，且其模糊度函数的形状和对应信号的频谱形状有关。尺度变化导致副本信号频谱的平移和伸缩，对于宽带平坦谱信号和单频信号来说，当尺度变大或缩小时，其模糊度函数值随之减小；对于梳状谱信号来说，当尺度变化使得副本信号频谱的梳齿刚好和发射信号频谱的梳齿交错时，其模糊度函数值变为0或接近于0，而当尺度变化使得副本信号频谱的梳齿和发射信号频谱的梳齿有重合时，其模糊度函数值又变大。这种周期性的变化导致梳状谱信号的模糊度函数呈钉板状。以下采取宽带脉冲串信号的模糊度函数实现方法实现PTLFM信号的模糊度函数［9］。

图4为典型PTLFM信号模糊度函数图，显然PTLFM信号的模糊度函数呈钉板状，是一种典型的多普勒敏感信号。

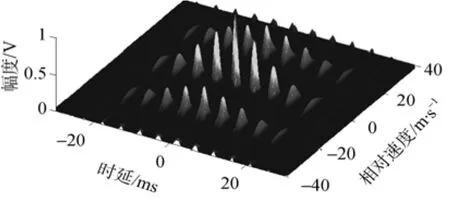
图4　典型PTLFM信号模糊度函数图Fig.4　Ambiguity function diagram of typical PTLFM signal

将η=1带入式（6），即得到PTLFM信号的时延模糊度函数

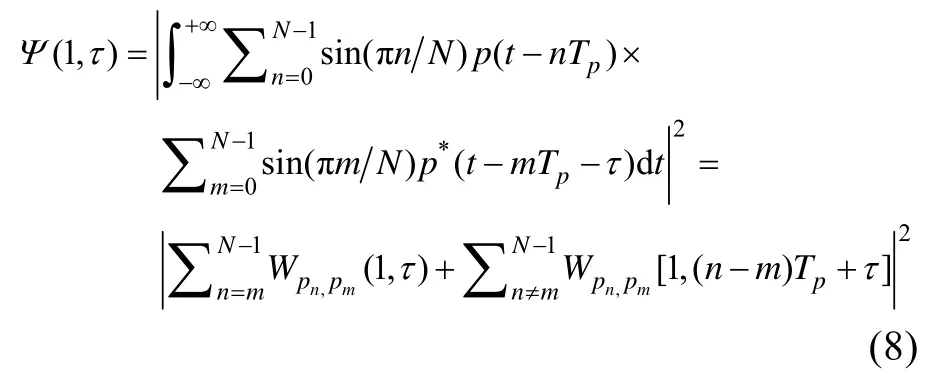
由式（8）可以看出，信号时延模糊度函数就是信号自相关取模求平方后的输出。由相关函数的性质可知：相邻波瓣之间的间隔为Tp，整个PTLFM的相关输出持续时间为2NTp，对于PTLFM信号来说，第一副瓣电平为

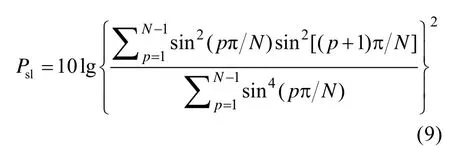
将子脉冲个数N=6代入上式，计算出第一副瓣电平为-1.584 dB。

图5为ptlfm_saw信号和ptlfm_syt信号时延模糊度函数。可以看出，无论是ptlfm_saw还是ptlfm_syt，其第一副瓣电平均为-1.584 dB，仿真结果和理论计算一致。ptlfm_syt信号模糊度函数由于主瓣相干累加而速度副瓣非相干累加，使得速度副瓣显著降低。以下通过仿真分析ptlfm_saw信号和ptlfm_syt信号的速度模糊度函数。

图6为ptlfm_saw信号和ptlfm_syt信号速度模糊度函数，显然ptlfm_syt信号的速度副瓣下降更快。

从式（6）可知，PTLFM信号的模糊度函数由自相关项和交叉项组成，自相关项形成了其主峰，交叉项组成了其旁峰，由于PTLFM信号是一种典型的时间分集信号，其时延分辨力和子脉冲的时延分辨力一致，对于填充线性调频信号的PTLFM信号来说，时延分辨力为0.44/B。

图5　ptlfm_saw信号和ptlfm_syt信号时延模糊度函数Fig.5　Time delay ambiguity function of the ptlfm_saw signal and the ptlfm_syt signal

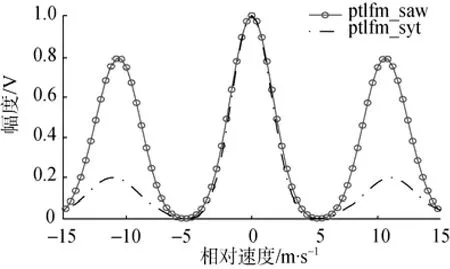
图6　ptlfm_saw信号和ptlfm_syt信号速度模糊度函数Fig.6　Velocity ambiguity function of the ptlfm_saw signal and the ptlfm_syt signal

信号的多普勒容限指的是模糊椭圆在尺度轴对应的最大值，速度容限可根据尺度和速度的关系换算出来。由于正弦平方包络PTLFM信号频谱梳齿宽度比矩形包络PTLFM信号频谱梳齿宽度大，那么正弦平方包络PTLFM信号的速度容限值也就比矩形包络PTLFM信号的速度容限大。采取相关检测算法时，选取速度容限大的信号将减小算法复杂度及硬件成本，对于实际工程应用具有积极作用。

图7为矩形包络和正弦平方包络PTLFM信号模糊椭圆图。可以看出，无论矩形包络还是正弦平方包络PTLFM信号，其时延分辨力一致，均为0.23 ms，而正弦平方包络PTLFM信号的速度容限比矩形包络PTLFM信号的速度容限宽约一倍。仿真结果和前面理论分析一致。

图7　矩形包络和正弦平方包络PTLFM信号模糊椭圆图Fig.7　Diagram of the fuzzy ellipse of the rectangular envelope and sine squared envelope PTLFM signals

2　PTLFM抗混响波形设计与分析

2.1PTLFM抗混响波形设计

PTLFM信号的谱峰间距是其信号参数设计的关键部分，想要获得好的探测效果，就要保证在不产生相邻频点混叠的条件下获得最多的谱线数目［6］。当主动声呐系统和目标相对速度为v，声速为c时，为使相邻频点不产生混叠，则必有

那么子脉冲个数可取为

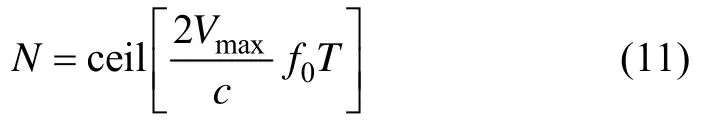
其中：f0是信号的中心频率；N是子脉冲个数；T是信号持续时间，为保证有一定测速模糊余量，Vmax的取值比实际情况的目标速度大一些。

假定信号总的持续时间为50 ms，工作频段6～8 kHz，目标运动速度为8 m/s，通过式（11）设计脉冲个数为5。

2.2混响信号产生

文中仿真海底混响采用点散射回波模型，将大量的散射元随机均匀分布到海底，根据它们与主动声呐平台的相对运动关系、相对位置和水声环境参数来确定每一散射元的回波属性，包括幅度、时延及多普勒尺度因子等，最后将所有散射元的散射信号在接收阵元处进行叠加得到某一通道的混响输出。

混响信号y（t）为所有散射元反射信号的叠加，即

式中：N为散射体的个数；A为散射体的回波幅度，它与发射信号的强度、散射元散射强度、散射元所代表的面积、发射和接收的波束指向性，传播扩展衰减以及海水吸收有关；ηnm为第n个散射体的多普勒尺度因子；τnm表示第m个阵元接收到第n个散射体散射信号的时延。

到阵元的距离为r的单个散射元所代表的面积为

所需的参数中，散射信号的幅度计算较为复杂，这里忽略海水吸收衰减和发射及接收的指向性等因素的影响，散射强度由兰伯特定律可得

式中：φ为散射体的俯仰角；比例常数u=10-2.7，则回波幅度为

回波的多普勒因子为

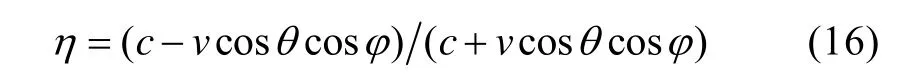
式中：θ为方位角；φ为俯仰角。回波的时延为

根据式（12）～式（16），设主动声呐在距海底30 m处，海底散射体（N=1000）在（150，1 500）的距离内随机均匀分布，即可产生混响信号。

图8为PTLFM信号混响时域频谱图。混响信号的持续时间约有1 s，其频谱有一定展宽。

图8　典型PTLFM混响时域频谱图Fig.8　Spectrum of the typical PTLFM reverberation signal in time domain and frequency domain

2.3PTLFM实测数据抗混响性能分析

本次实测数据通过消声水池中接收换能器接收声靶发射的信号获得，声靶发射的信号用以模拟目标辐射的回波信号。消声水池是体积为（20 ×8×7）m3的立方体型，水池深8 m，接收换能器和声靶位于水面以下2 m处，换能器和声靶的水平间距为3 m。由于水面、侧壁和水底覆盖消声尖劈，导致水下环境几乎无混响产生，试验当中的混响由仿真实现。

如图9为ptlfm_saw和ptlfm_syt回波信号时域图，这里ptlfm_saw和ptlfm_syt回波出现在200 ms处，信混比SRR=-5 dB，混噪比RNR=5 dB（混响占优），噪声为高斯白噪声。从图中可以看出，目标回波完全淹没在混响和噪声中。

图9　PTLFM回波时域Fig.9　PTLFM echo signal in time domain

以下分别比较目标速度为0 m/s、5 m/s、10 m/s时ptlfm_saw信号和ptlfm_syt信号在复杂背景（混响占优）下的匹配滤波输出效果。

混响背景下目标速度0 m/s、5 m/s、10 m/s时ptlfm_saw和ptlfm_syt信号匹配滤波输出如图10、图11和图12所示。

图10　目标速度0 m/s时ptlfm_saw信号和ptlfm_syt信号匹配滤波输出Fig.10 The ptlfm_saw signal and ptlfm_syt signal matched filter output when target speed is 0 m/s

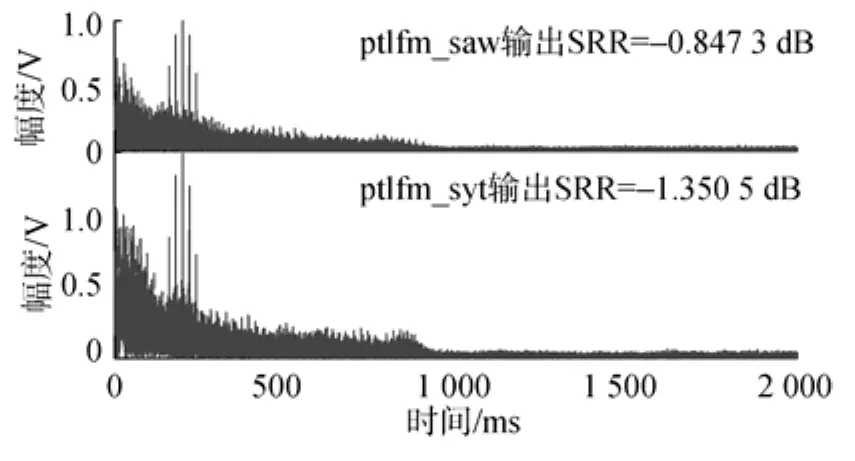
图11　目标速度5 m/s时ptlfm_saw信号和ptlfm_syt信号匹配滤波输出Fig.11　The ptlfm_saw signal and ptlfm_syt signal matched filter output when target speed is 5 m/s

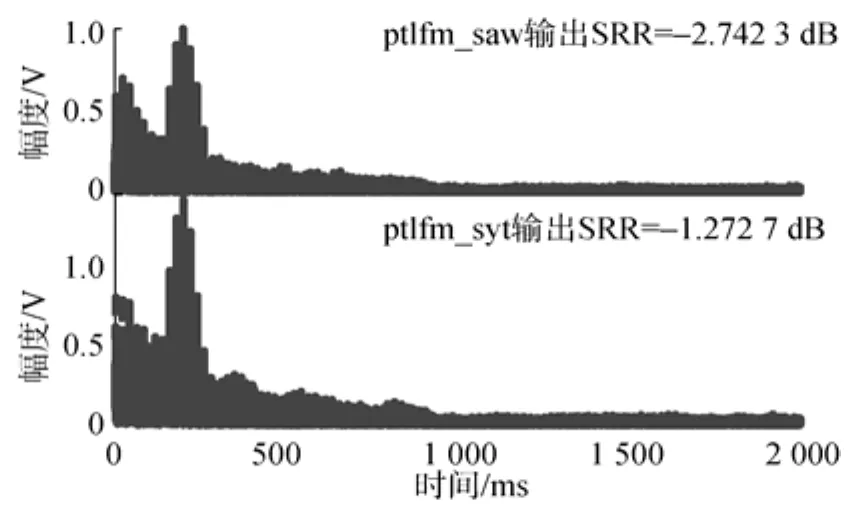
图12　目标速度10 m/s时ptlfm_saw信号和ptlfm_syt信号匹配滤波输出Fig.12 The ptlfm_saw signal and ptlfm_syt signal matched filter output when target speed is 10 m/s

可以看出，目标速度为0 m/s和5 m/s时，ptlfm_saw信号比ptlfm_syt信号的匹配滤波效果好，也就是具有更好的抗混响性能；目标速度为10 m/s时，ptlfm_syt信号比ptlfm_saw信号具有更好的抗混响性能。

3　结束语

文中结合理论、仿真和实测数据分析，研究了PTLFM信号的频谱及模糊度函数特性；并提出采取宽带对称三角状调频形式的PTLFM信号以提高信号的混响抑制性能；根据抗混响波形设计完成波形设计，在复杂背景环境（强混响和高斯白噪声背景）下完成了信号的检测。理论分析、仿真结果和实测数据处理结果表明：对于静止或运动目标来说，锯齿状调频形式PTLFM信号的混响抑制性能优于对称三角状调频形式PTLFM信号的混响抑制性能；对于目标运动速度为PTLFM模糊度函数速度副瓣最大值来说，相比较锯齿状调频形式PTLFM信号而言，对称三角参考文献：

状调频形式PTLFM信号由于降低了速度副瓣从而提高了检测性能。文中研究的内容对混响背景下波形设计有着积极的应用价值。

［1］Pecknold S P，Renaud W M，McGaughey D R，et al.Improved Active Sonar Performance Using Costas Wave-Forms［J］.IEEE Journal of Oceanic Engineering，2009，34（4）：559-574.

［2］Collins T，Atkins P.Doppler-sensitive Active Sonar Pulse Designs for Reverberation Processing［J］.IEEE Processing Radar，Sonar Navig ，1998 ，145（6）：347-353.

［3］Doisy Y，Deruaz L.Reverberation Suppression Using Wideband Doppler-Sensitive Pulses［J］.IEEE Journal of Oceanic Engineering，2008，33（4）：419-433.

［4］Mathieu E，Colin G D，Beerens P S.False-Alarm Reduction for Low-Frequency Active Sonar With BPSK Pulses：Experimental Results［J］.IEEE Journal of Oceanic Engineering，2011，36（1）：53-60.

［5］张容权，杨建宇，熊金涛，等.对称三角线性调频连续波信号模糊函数分析［J］.电子学报，2004，32（3）：353-356.

Zhang Rong-quan，Yang Jian-yu，Xiong Jin-tao，et al.Symmetrical Triangular Linear Frequency Modulation Continuous Wave Signal Fuzzy Function Analysis［J］.Chinese of Journal Electronics，2004，32（3）：353-356.

［6］Lin Z B.Wideband Ambiguity Funcfibn of Broadband Signals［J］.Journal of the Acoustical Society of America，1988，83（6）：2108-2116.

［7］梁国龙，张瑶，付进，等.新型主动声呐梳状谱信号设计［J］.哈尔滨工程大学学报，2012，33（3）：302-307.

Liang Guo-long，Zhang Yao，Fu Jin，et al.New Comb Waveforms for Reverberation Suppression［J］.Journal of Harbin Engineering University，2012，33（3）：302-307.

［8］姚东明，蔡志明.主动声纳梳状谱信号研究［J］.信号处理，2006，22（2）：256-259.

Yao Dong-ming，Cai Zhi-ming.Active Sonar Comb Spectrum of Signal［J］.Signal Processing，2006，22（2）：256-259.

［9］岳雷，梁红，杨长生.一种宽带脉冲串信号模糊度函数实现方法［J］.鱼雷技术，2014，22（2）：96-99.

Yue Lei，Liang Hong，Yang Chang-sheng.A Realization Method for Ambiguity Function of Wideband Pulse Train Signal［J］.Torpedo Technology，2014，22（2）：96-99.

（责任编辑：杨力军）

Pulse Trains of Linear Frequency-modulated Signal and Its Detection Performance

YUE Lei1，2
（1.Kunming Shipbuilding Equipment Research &Test Center，Kunming 650000，China；2.School of Marine Science and Technology，Northwestern Polytechnical University，Xi′an 710072，China）

For active sonar reverberation suppression，the characteristics of pulse trains of linear frequency-modulated （PTLFM）signal is studied in terms of time domain，frequency domain，and ambiguity function，and the wideband symmetrical triangular frequency-modulated PTLFM signal is adopted to improve the reverberation suppression performance on speed sidelobe.PTLFM waveform design is completed following the comb spectrum signal design requirements，and detection of target with different velocity is performed by making use of measured data of PTLFM signal with complicated background.Theoretical analysis，simulation results and measured data show that the reverberation suppression performance of the sawtooth PTLFM signal is better than that of the symmetrical triangular PTLFM signal for static or moving target，while the reverberation suppression performance of the symmetrical triangular PTLFM signal is better for the target whose velocity is the maximum speed sidelobe of its ambiguity function.This study may provide a reference for anti-reverberation waveform design.

pulse trains of linear frequency-modulated（PTLFM）；ambiguity function；reverberation suppression；waveform design；speed sidelobe

TJ630.34；TN911.7

A

1673-1948（2015）04-0285-06

2015-05-13；

2015-06-10.

岳雷（1988-），男，硕士，主要研究方向为信号与信息处理.

PTLFM信号混响抑制性能更强。本文的研究可以为抗混响波形设计提供参考。