有缺陷的多接收阵合成孔径声呐成像技术

张远彪，朱三文

（中国人民解放军91388部队，广东 湛江，524022）

有缺陷的多接收阵合成孔径声呐成像技术

张远彪，朱三文

（中国人民解放军91388部队，广东 湛江，524022）

试验过程中不可预测的原因可能会导致接收基阵中的一个或多个接收阵元失效，进而严重影响整个合成孔径声呐（SAS）系统的性能。基于此，提出了一种有缺陷的多接收阵SAS成像方法，首先基于线性预测方法对失效阵元的回波信号进行重构，然后再进行合成孔径成像处理。该方法可以较好地解决阵元失效带来的图像畸变问题，仿真试验验证了其有效性和可行性。

合成孔径声呐（SAS）；多接收阵；缺陷阵元；图像畸变

0　引言

目前，国内外均采用多接收阵技术［1-3］来解决测绘速率和方位向分辨率之间的矛盾。为了使系统具有更好的灵活性，声呐系统的接收基阵普遍采用模块化设计，因此可以通过不同个数接收子阵模块的组合，实现声呐系统设计者对分辨率、探测距离、测绘率或者平台速度的需求。

从声呐基阵设计上来说，为了保证各接收子阵紧密排列时的声学特性，各接收子阵模块的两端可能会设计一个既不发声也不接收信号的哑阵元；当然，各接收子阵模块之间也可以不采用紧密排列的方式，而是在2个相邻的子阵模块之间设计1个接收阵元大小的间隙来代替上述的哑阵元。例如，挪威SENSOTEK干涉合成孔径声呐（synthetic aperture sonar，SAS）系统［4］的每个声呐接收子阵有32个阵元，每个阵元长度为1.5 cm，整条接收基阵由3条接收子阵组成，每2条子阵间相隔1个接收阵元的长度，故全长147 cm。另一方面，在试验过程中，可能存在着诸如恶劣的自然环境、人为因素以及硬件的使用寿命等许多不确定的因素，使得满足系统设计要求的长接收基阵（未采用模块化设计）中1个或者多个接收阵元发生物理性损坏；这种损坏可能来自于阵元本身，也可能是与这些接收阵元相对应的接收机通道电子电路发生故障。如果直接使用这种有缺陷的接收基阵的回波数据进行成像处理，将会抬高图像旁瓣，进而可能导致假目标出现和图像对比度下降。对于这种存在失效阵元的声呐基阵，最简单的故障排除法就是对失效阵元进行检修或替换，但笨重的水声设备回收和布放较为繁琐，检修或更换一般都需要较长的时间，所以在不影响整个系统正常工作的前提下寻求一种应急的补救措施就显得尤为重要。对于存在失效阵元的阵列信号处理来说，既可以通过优化正常阵元的权值来获得阵元失效前一致的性能［5-6］，也可以通过正常阵元的输出重构失效阵元的信号［7］。对于多接收阵SAS来说，失效阵元将会周期性的出现；如果采用第1种方法对场景进行成像，那么每得到1个像素的结果，都必须重新计算一次权值，因此较为复杂。文中将基于第2种方法，采用线性预测方法［8］，首先重建失效阵元的回波信号，再进行合成孔径成像处理［9］。这种方法可以较好地解决阵元失效带来的图像畸变问题，仿真试验验证了文中方法的有效性和可行性。

1　问题描述

假设SAS系统的声呐接收基阵由2个接收子阵模块组成，接收子阵模块如图1 （a）所示，每个接收子阵模块均有25个接收阵元，其中模块的1个端点处设计有1个哑阵元，每个接收阵元方位向实孔径为4 cm。

图 1 （b）为2个模块组成的满足系统要求的接收基阵，填充黑色的矩形单元表示发射阵，其方位向长度为8 cm；2个接收基阵模块之间的矩形单元表示1个哑阵元或者表示间隔接收阵元长度的一段距离。

图1　声呐系统接收基阵Fig.1　Receiver array of sonar system

图 1所示的声呐基阵系统也可这样描述：声呐接收基阵由51个接收阵元组成，每个接收阵元方位向实孔径为4 cm，整条基阵长度为204 cm，由于试验过程中某些不确定原因，接收基阵中第25号、第26号和第27号接收阵元（或者对应的接收机通道电子电路）发生故障，从而使得记录的这3路接收信号为零。

2　有缺陷的多接收阵SAS成像

2.1基于线性预测的成像方法

文中在进行合成孔径成像处理之前，先利用线性预测的方法［8］重构失效阵元的信号。设x（n）在n时刻之前的p个数据｛x（n-p），x（n-p+1），…x（n-1）｝已知，希望利用这p个数据来预测n时刻的值x（n），这里采用线性预测的方法来实现。记xˆ是对真实值x（n）的预测，那么

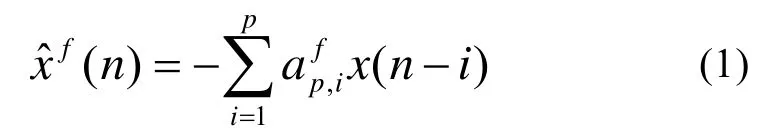
式中，p表示预测阶数；上标f强调式（2）是前向预测。

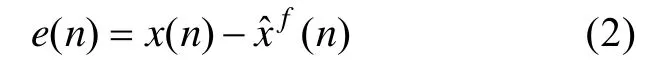
因此，总的预测误差功率为

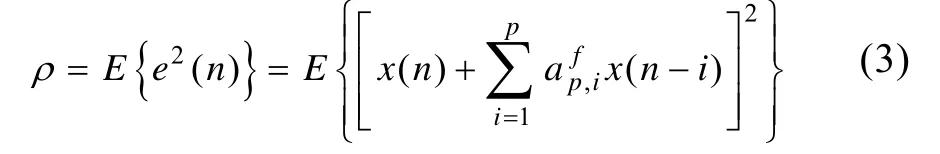
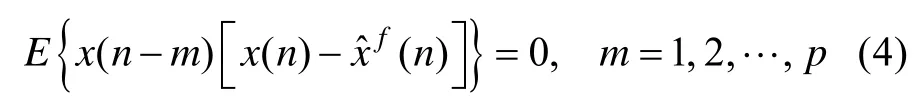
由上式可得

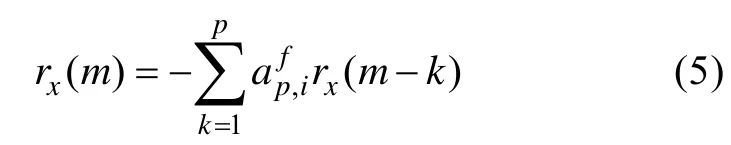
将式（5）代入式（3），可得

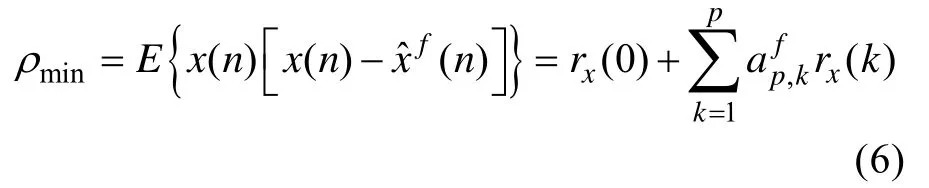
式（5）和式（6）称为线性预测的维纳-霍夫方程。

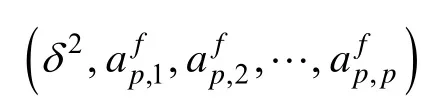
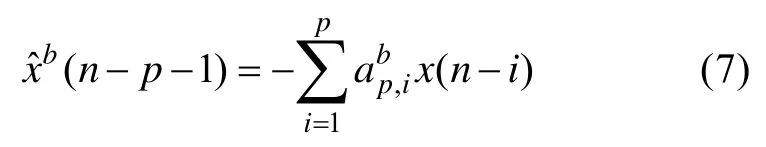
式中：上标b强调式（7）是前向预测；后向预测器与前向预测器的系数满足时反共轭关系。

Burg算法［10］是较早提出的建立在数据基础上的AR系数求解的有效算法，其思想是在列文森-杜宾（Levinson-Durbin）算法基础上，令前后向预测误差功率之和最小。这里将使用Burg算法来计算线性预测器的系数。

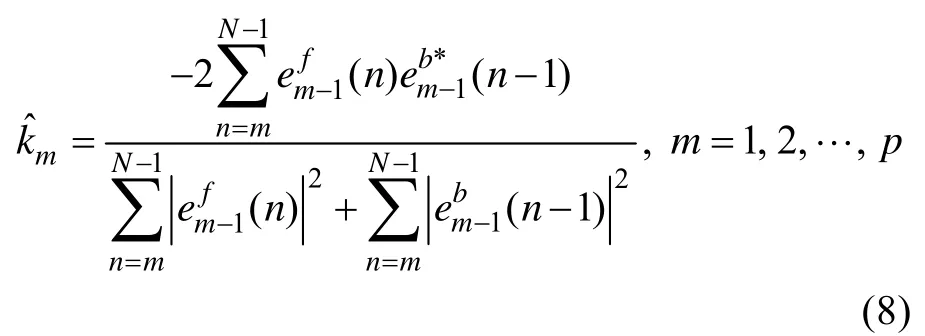
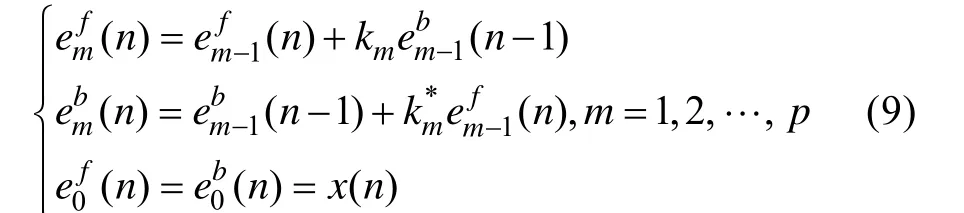
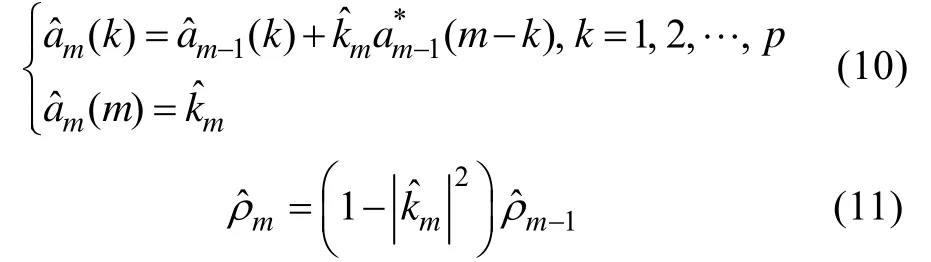
第5步：重复上述过程，直到m=p，求出了所有阶次时的AR参数。

针对第一部分所提出的问题，利用每个脉冲内所接收到的多个接收阵元的回波数据，采用前向预测的方法估计第25号接收阵元的数据，采用后向预测的方法估计第27号接收阵元的数据；而对于第26号接收阵元，其回波估计值用前、后向预测器的均值来代替。按照上面介绍的方法，对3个失效阵元的数据恢复后，便转化为多接收阵SAS成像问题［9］，其成像流程如图2所示。

为节约篇幅，这里对CS（chirp sealing）成像算法不再予以赘述，具体成像过程和对应的相位补偿项参见文献［9］。

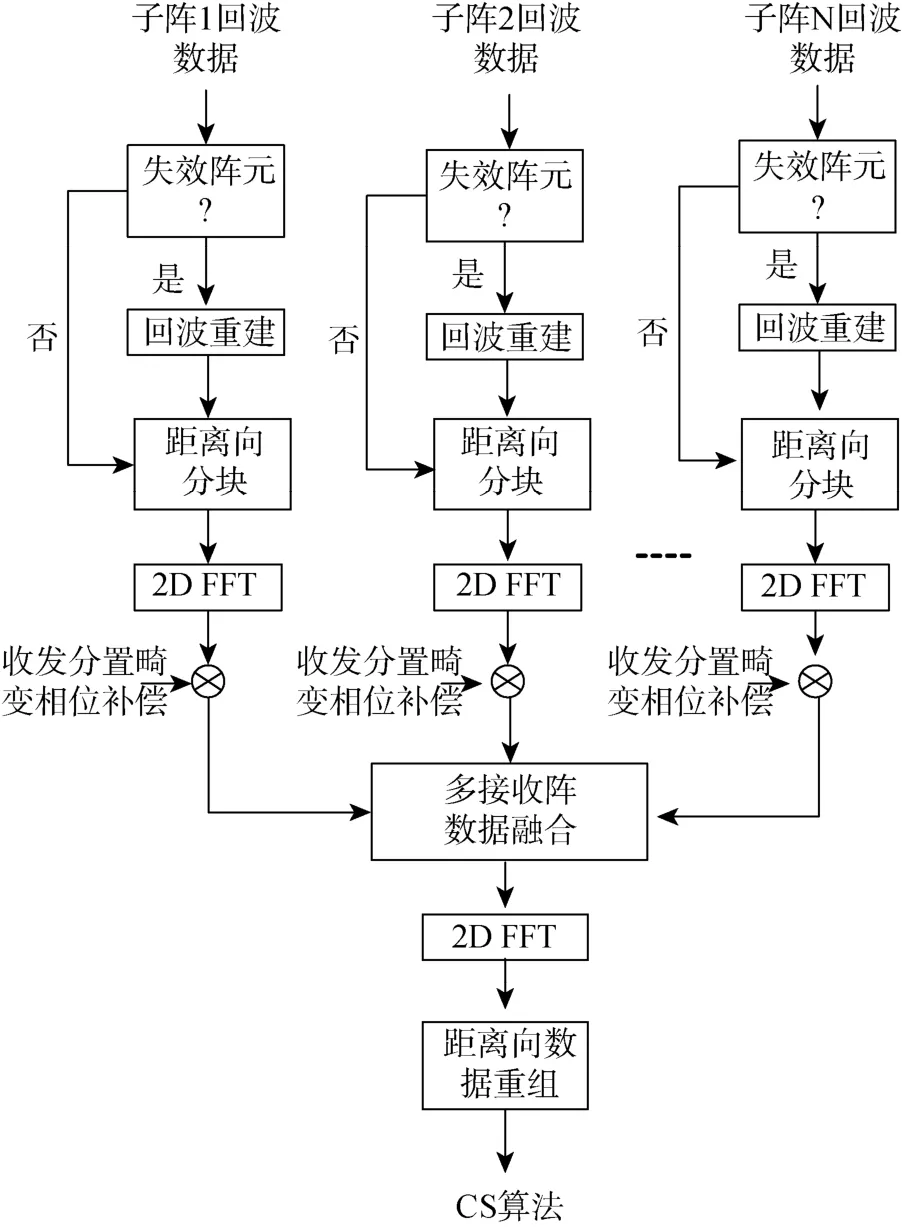
图2　多接收阵合成孔径声呐CS算法流程图Fig.2　Flow chart of chirp scaling（CS）algorithm for multi-receiver synthetic aperture sonar（SAS）

2.2预测阶数的选择

线性预测器的阶数一般是不可提前预知的，需要事先选定一个稍大得到值，在递推的过程中确定。实际上，AR模型的最小预测误差功率ρmin是递减的。直观地讲，当最小预测误差功率ρmin达到指定的期望值，或是不再发生变化时，此时的阶次即是应选的正确阶次。

由于ρmin是单调下降的，因此，往往不好确定ρmin的值降到多少才合适。为此，这里介绍2个常用的准则。

1）最终预测误差准则

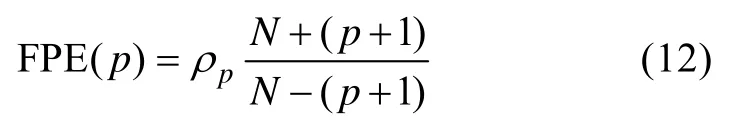
2）信息论准则

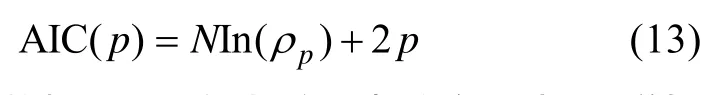
式中，N为数据xN（n）的长度，当阶次p由1增加时，FPE（p）和AIC（p）都将在某一p处取得极小值，将此时的p定位最合适的阶次p。在实际应用时发现，当数据较短时，给出的阶次偏低，且二者给出的结果基本上是一致的。应该指出，上面2式仅为阶次的选择提供了一个依据。在实际引用中，还可以根据需求多次比较最小误差功率予以确定。

3　试验验证

为验证所提方法的有效性，设计仿真试验如下。发射的线性调频信号中心频率为150 kHz，带宽为20 kHz，信号脉冲宽度为20 ms，脉冲重复时间为0.32 s，平台速度为2.5 m/s，发射阵元方位向长度为8 cm，接收阵元方位向长度为4 cm，接收基阵长为160 cm。在空间设置1个理想点目标，其2D坐标为 （75 m，15 m），基于CS算法［9］的合成孔径成像结果如图3所示，其中图3（a）为接收阵元全部正常情况下的成像结果；图3（b）为存在3个失效阵元情况下的成像结果；图 3（c）为失效阵元信号重构后的成像结果；图 3（d）为点目标成像结果方位向剖面图。

观察图3 （b）可以发现，当接收基阵中存在失效阵元时，图像旁瓣明显增大，因而很可能导致假目标的出现。而图3 （c）所示的失效阵元数据重构后的成像结果与理想情况下的成像性能基本相当，图3 （d）所示的方位向剖面图也证明了文中方法的有效性。

在2D成像场景中设置4个理想点目标，其空间布局如图4（a）所示，基于CS算法的成像结果如图4（b）、图4（c）和图4（d）所示。其中图4（b）为阵元未损坏情况下的理想点目标成像结果，图4（c）为接收阵元存在故障时直接利用回波数据进行成像处理的聚焦结果，图4 （d）为接收阵元存在故障时首先重建失效阵元回波数据再进行成像处理的聚焦结果。观察图4所示的成像结果，可以发现如果不对基阵中的失效阵元进行处理，那么其成像结果就会产生畸变，而文中所给出的方法可以较好地解决这个问题。

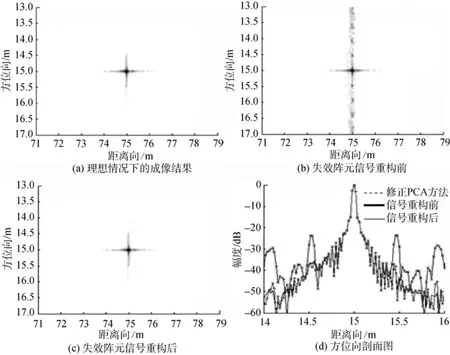
图3　理想点目标聚焦结果Fig.3　Results of focusing on ideal point target

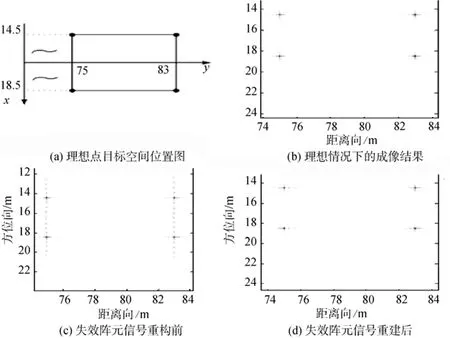
图4　点目标成像结果Fig.4　Imaging results of point target

4　结束语

针对接收基阵中1个或者多个阵元可能失效的情况，给出了一种基于线性预测的有缺陷的多接收阵SAS成像方法，并以CS算法为例进行了仿真试验，结果表明该方法可以有效地解决缺陷阵带来的旁瓣电平抬高和图像对比度下降的问题，为进一步提高SAS系统的性能提供依据。

［1］Hayes M P，Gough P T.Synthetic Aperture Sonar：a Review of Current Status［J］.IEEE Journal of Oceanic Engineering，2009，34（3）：207-224.

［2］张学波，唐劲松，张森，等.四阶模型的多接收阵SAS距离-多普勒成像算法［J］.电子与信息学报，2014，36（7）：1592-1598.

Zhang Xue-bo，Tang Jin-song，Zhang Sen，et al.Four-order Polynomial Based Range-Doppler Algorithm for Multireceiver Synhetic Aperture Sonar［J］.Journal of Electronics &Information Technology，2014，36（7）：1592-1598.

［3］Zhang X B，Tang J S，Zhong H P.Multireceiver Correction for the Chip Scaling Algoirhtm in Synthetic Apeture Sonar［J］.IEEE Journal of Oceanic Engineering，2014，39（3）：472-481.

［4］Hansen R E，Sæbø T O，Callow H J，et al.The SENSOTEK Synthetic Aperture Sonar：Results form HUGIN AUV Trials［R］.FFI-repport，Norway，2007，6.

［5］Er M H，Hui S K.Beamforming in Presence of Element Failure［J］.Electronics Letters（S0013-5194），1991，27（3）：273-275.

［6］Sim S L，Er M H.Sidelobe Suppression for General Arrays in Presence of Element Failures［J］.Electronics Letters （S0013-5194），1997，33（15）：1278-1280.

［7］Mailloux R J.Array Failure Correction with a Digitally Beamformed Array［J］.IEEE Transactions on Antennas and Propagation（S0018-926X），1996，44（12）：1543-1550.

［8］胡广书.数字信号处理——理论、算法与实现［M］.第2 版.北京：清华大学出版社，2007.

［9］张学波，唐劲松，钟何平.合成孔径声呐多接收阵数据融合CS成像算法［J］.哈尔滨工程大学学报，2013，34（2）：240-244.

Zhang Xue-bo，Tang Jin-song，Zhong He-ping.Chirp Scaling Imaging Algorithm for Synthetic Aperture Sonar Based on Data Fusion of Multi-receiver Array［J］.Journal of Harbin Engineering Universtiy，2013，34（2）：240-244.

［10］Burg J P.Maximum Entropy Spectral Analysis［C］//In Processing 37th Meeting of Society Exploration Geophysicists.Oklahoma City，1967，10.

（责任编辑：杨力军）

Imaging of Multi-receiver SAS with Faulty Array Element

ZHANG Yuan-biao，ZHU San-wen
（91388thUnit，The People′s Liberation Army of China，Zhanjiang 524022，China）

One or several array element in array receivers may lose efficacy due to unpredictable factors during testing process，and hence seriously affect performance of whole synthetic aperture sonar （SAS）system.This paper proposes an imaging method of multi-receiver SAS with faulty array element to resolve the image distortion caused by the invalid receivers.In this method，the signal from the invalid array element is reconstructed based on linear prediction，then synthetic aperture imaging processing is performed.Simulation results show the validity and feasibility of the proposed method.

synthetic aperture sonar（SAS）；multi-receiver；faulty array element；image distortion

TJ630.34；TM46

A

1673-1948（2015）04-0280-05

2015-04-13；

2015-05-18.

张远彪（1973-），男，工程师，主要研究方向为试验总体技术.