基于换乘次数最少算法的公交查询平台

芦娜 朱丽华

摘要：该文依据安阳市目前的交通现状，指出游客出行更多考虑的是换乘次数。本文同时分析了Dijkstra算法的局限性，并提出了基于换乘次数最少算法。最后又对平台的设计模块进行了介绍，取得了一定的实际效果。

关键词：公交；换乘；最优路径

中图分类号：TP311 文献标识码：A 文章编号：1009-3044（2015）05-0201-02

The Design and Implementation of Anyang Intelligent Public Transportation Platform

LU Na， ZHU Li-hua

（Computer Science and Engineering Department， School of Mechanical Engineering AnYang Institute of Technology， Anyang 455000， China）

Abstract： This paper pointed out that the least transfer is the most important， based on the present situation of transportation in Anyang and the statistic about psychological inquisition of passengers trip. This paper analyzed the Dijkstra algorithm is not optimal route selection of public traffic network.， And presented the algorithm about optimal route selection based on the least transfer. Last， This paper discussed the design of each function module.

Key words： public transport； transfer algorithm； optimal path

公共交通是与人民群众生活息息相关的重要基础设施之一。安阳市位于豫北地区，其历史悠久。安阳目前的交通现状是：私家车迅猛猛增，非机动车不按道行驶等，使安阳的交通越来越拥堵，人们的出行也越来越不方便。本文试以安阳市公共交通为基础，研发了一种经济实用的公交信息查询平台方便人们出行。

1 公交信息查询平台的形式

目前有四种通用的公交查询平台：

1）出行前的查询：主要是静态的交通信息，人们在乘车前可以通过手机、计算机等途径查询公交车辆的线路、途径站点等信息。

2）车站/站牌的公信息查询：人们可以通过在车站或者站牌查询一些公交信息。

3）公交车上信息查询：主要是动态信息，通过车内电子显示板，能显示车辆目前的位置、到站时间以及一些换乘信息等。

4）综合的信息查询：属于以上三种的综合，主要通过集成多个服务系统的实时数据。

2 公交信息的换乘算法

在公交网络的数学描述方面，可以用对偶图描述，也可以从街道的地理数据产生公交线路和站点情况。出行最优路径算法以最短路径算法为基础，常用的最短路径算法主要有Dijkstra算法、Ford算法、Floyd算法[1]、Moore算法等。下面以Dijkstra算法为例。

2.1 Dijkstra算法

Dijkstra算法在计算机网络拓扑路径选择以及GIS中应用较广泛，因为其能较好地适应网络拓扑的变化。但是对于公交网络来说，Dijkstra算法具有数据结构复杂，算法时间长的缺陷。另外由于公交换乘中的特殊性，如果采用 Dijkstra算法，只要图中两个结点之间有边存在，它就会进行搜索，忽略了乘客的换乘次数，这样所计算出来的结果可能是两个站点之间的最短距离，但需要换乘好几次才能到达。这对乘客来说一定不是最佳的选择，甚至没有实际意义。

2.2 基于换乘最少算法

人们出行首要考虑的是换乘次数最少，然后是出行距离、时间等最短。所以本平台将换乘最少作为最优路径算法的第一约束条件，出行距离最短作为第二约束条件。

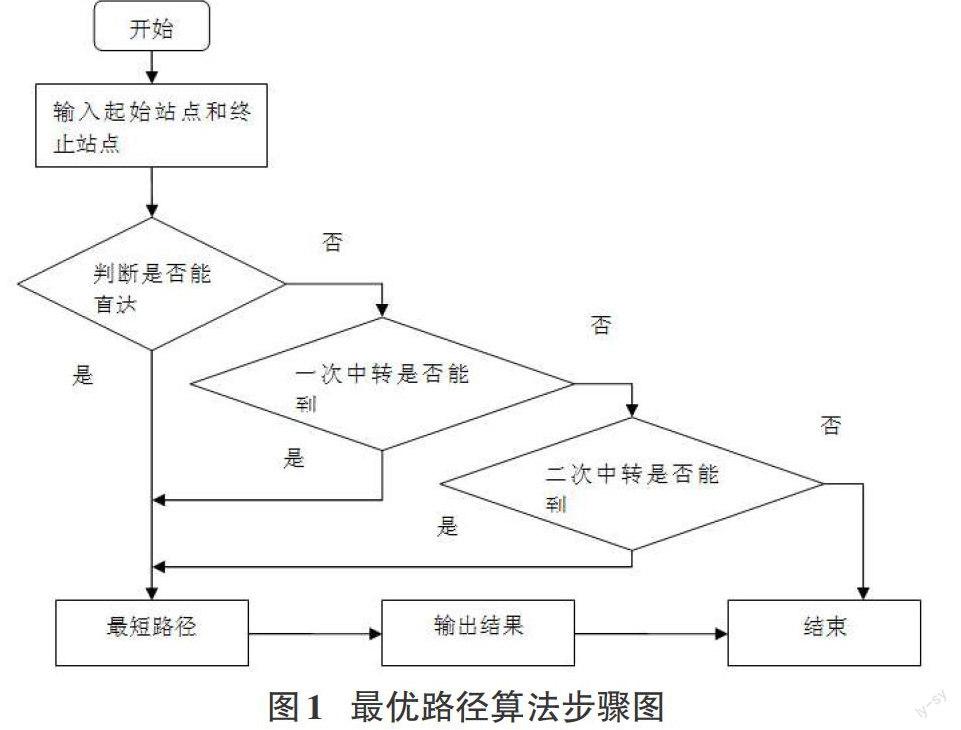
输入起始站点和终止站点时，该平台将会对输入的站点进行判断，如果起始站点和终止站点刚好在同一条公交线路上，直接把结果输出，该条线路就是最短路径；否则，需判断两个站点之间的线路是否有相同的站点，若只有一条则说明在此点经过一次中转就能够到达目的地，则这条线路就是我们要求的最短路径；若有多条路径可以到达则选择距离最近的路径作为最短路径，输出结果。再则，判断是否有公交线路和起始站点和终止站点所在的线路相交，若有，则说明经过两次中转能够到达目的地[4]。最后经过两次中转还无法到达，在实际生活中没有实际意义，本平台就不加考虑了。图1为基于换乘最少算法的步骤图。

3 平台设计与实现

3.1 数据库设计

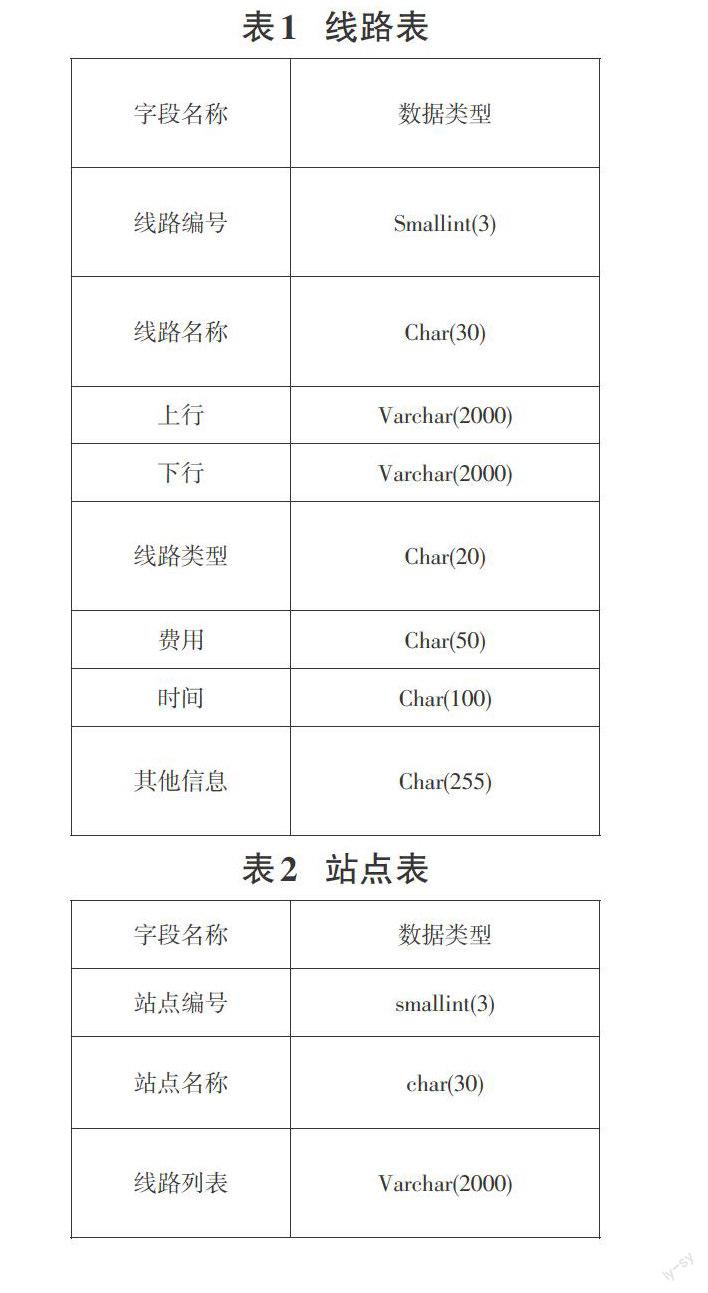
该平台的数据库设计中，根据规范，建立了相应的数据表为：公交线路表、公交站点表等，其结构如表1，2所示。

3.2 功能模块实现

本平台的功能模块主要包括线路查询模块、站点查询模块、换乘查询模块等。

3.2.1 线路查询模块

该模块能够实现根据公交车线路的名称来查询公交线路信息。例如，在查询页面线路查询输入1，单击“线路查询”按钮，即可获得1路公交的详细信息。

3.2.2 站点查询模块

该模块主要是实现查询经过某站点的公交车的信息，可以进行模糊查询。例如，可以在站点查询处输入“安阳工学院”，点击“查询”按钮，就可以得到所有经过“安阳工学院”的公交车的详细信息。

3.2.3 换乘查询模块

该模块主要是完成游客公交车换乘方案的查询。模块在查询的时候，算法按照先直达后一次换乘，最后是二次换乘，进行数据的优化，把相同的站点去掉，来实现最终查询。例如，在查询页面公交换乘查询在“起点名称”处输入“安阳工学院”和“终点名称”处输入“三角湖”，单击“换乘查询”按钮，即可显示两个站点乘车方案。

4 结束语

本文是以安阳市交通现状为背景进行的公交信息查询平台的研究。本文对公交换乘算法等关键技术进行了研究，最后选择了基于换乘次数最少算法。本平台以安阳市的公共交通现状为出发点，完成了公交线路、站点、换乘等信息的查询功能。平台虽然实现了安阳市内公共交通信息的查询，但是仍需要进一步改进，如：平台如何移植到移动终端。

参考文献：

[1] 汪江红. 公交换乘系统研究及评价[D]. 成都： 西南交通大学，2006： 50-53.

[2] 严蔚敏， 吴伟民. 数据结构[M]. 北京：清华大学出版社， 1997： 155-159.

[3] 李擎， 谢四江， 童新海， 等. 一种用于车辆最短路径规划的自适应遗传算法及其与Dijkstra和A*算法的比较[J]. 北京： 北京科技人学学报， 2006， 25（l）： 1084-1085.

[4] Wu Qiujin， Hartley J. Using K-Shortest Paths Algorithms to Accommodate User Preferences in the Optimization of Public Transport Travel [C」.The 8th International Conference on Applications of Advanced Technologies in Transportation Engineering. U.S： ASCE， 2004： 181-186.