一种基于图匹配的求解可满足性问题的算法
于千城
摘要:信息传播算法求解可满足性问题时具有良好的有效性,能使难解区域变窄。在信息传播算法的设计中,是将变量的联合概率分布分解为变量子集上的局部函数的乘积形式。称局部函数为因子(factor),每一个因子依赖于一个变量子集,将变量联合分布的这一因子形式表示为图模型——因子图(factor graph)。信息传播算法是通过因子图上的边传递概率消息,这种消息传递有两种方式:变量结点传递给因子结点的消息和因子结点传递给变量结点的消息。从每个结点传出的消息由传入该结点的消息决定,通过某种迭代策略对消息进行更新。当这种消息迭代过程收敛到某一固定点时,利用某种规则(如,最小熵、最大积、最大匹配)对问题进行求解。本文提出一种利用最大匹配规则求解因子图上的信息传播算法的收敛性及算法迭代步数的上界估计方法,根据对算法的收敛性分析,在对问题解的精确性影响不大的前提下,仅需要给出算法合理的迭代步数或者强迫算法终止,使得算法提前结束,有助于求解可满足性问题算法性能的更进一步优化。
关键词:信息传播算法;可满足性问题;收敛性;因子图;最大匹配
中图分类号:TP316 文献标识码:A 文章编号:1009-3044(2015)05-0209-04
An Algorithm for Solving The Satisfiability Problem Based on Graph Matching
YU Qian-cheng
(Department of Computer Science,Beifang Ethnic University,YinChuan 750021,China)
Abstract: Message passing algorithms are very effective in finding satisfying assignments for SAT instances, and hard region become narrower. In the design of the Message passing algorithms, the joint probability distribution of the variables is decomposed into the product form of the local function of the variable quantum set. The local function is a factor, and each factor is dependent on a variable subset, which is represented as a graph model factor.Message passing algorithms is a kind of message passing through a factor graph, which has two ways: the variable node is passed to the message and the factor node of the node. The message from each node is determined by the decision of the incoming message, and the message is updated by an iterative strategy. When the convergence of this kind of message is fixed to a fixed point, the problem is solved by using some rules (e.g., minimum entropy, maximum product and maximum matching). In this paper, we propose a method to estimate the convergence and the upper bound of the algorithm. Based on the convergence analysis of the algorithm, we only need to give a reasonable number of iteration steps or forced the algorithm to terminate.
Key words: Message Passing Algorithms;Satisfiability Problem;Convergence;Factor Graph; Maximum Matching.
SAT 问题是计算机科学中的核心问题,其理论及其应用研究,是计算机与数理逻辑界学者共同关注的一个重大问题[1]。在工程技术、人工智能、并发控制等领域中,诸多带有协调性(或一致性)检验、组合优化等问题均可以编码到SAT 问题[2]。在SAT 问题理论及应用方面的研究,包括硬件模型检测,软件模型搜索,可信计算,等价性检测,安全性验证,证明系统,证明复杂性,搜索算法,启发式算法,算法分析,难解实例,随机公式,问题编码,求解器设计,简化器设计,实例研究与工业应用等。大型数据库的维护,大规模集成电路的自动布线,机器人动作规划等,都涉及SAT 问题[3]。
随着SAT 问题的深入研究,各类具有特殊结构的SAT 问题受到越来越多的学者重视规则结构的实例对应的因子图是一个规则结构的二部图(如,k-CSP 实例、k-SAT实例等,它们的因子图是一个规则结构的二部图),借助于规则二部图的结构性质,便于理解和分析信息传播算法的数学原理及性能。图论中规则二部图的许多良好的性质对于研究实例的结构性质具有潜在的作用;基于这种规则结构的实例,信息传播算法的收敛性研究则更为具体和直观;在规则结构的因子图上,有助于研究与分析消息传播方式与迭代过程中消息的稳定性,这对利用信息传播算法求解可满足性问题非常有效,几乎能够在多项式时间内给出解。
1 基本知识
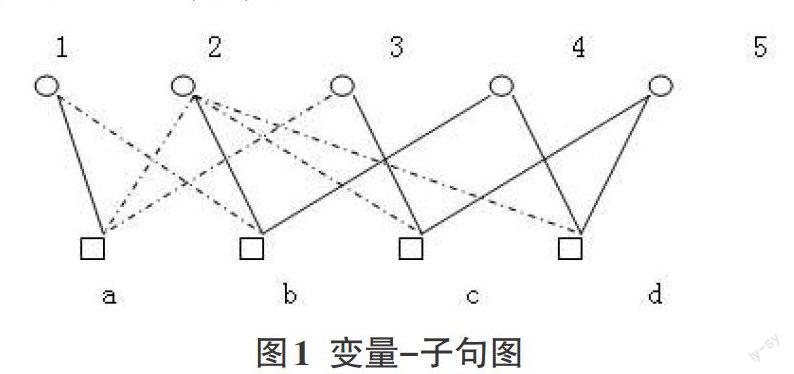
设[F={a1,......,am}]为一个k-CNF公式,含有n个变量[x1,......,xn]。公式F可以用一个二分图[G=(X?A,E)]表示,称为因子图 (factor graph)或变量-子句图,其中,变量结点集[X={1,......,n}],子句结点[A={a1,......,am}]。G中的边分为两类:实边和虚边。有时用a,b,c,d,…表示子句结点,用i,j,k,…表示变量结点。
实边:[(ai,j)∈E?]子句[ai]含正文字[xj];
虚边:[(ai,j)∈E?]子句[ai]含负文字[?xj]。
例1.1:
[F={(x1∨?x2∨?x3),(?x1∨x2∨x4),(?x2∨x3∨x5),(?x2∨x4∨x5)}={a1,a2,a3,a4}]
的因子图[G=(V,E)]为:
图1 变量-子句图
公式F的子公式指由F的部分子句所构成的公式。若子句中含有一对互补文字,称该子句为重言子句。在公式中删去重言子句后,不影响公式的可满足性。var(F)和cl(F)表示出现在公式F中变元的集合、F中子句的集合。#var(F)和#cl(F)分别表示公式F中的变元个数和子句的个数。
可满足性问题是指,给定命题变元集M={x1,x2,…,xn}上的一个合取范式(简称CNF)公式F,判断是否存在真值指派v,使F是可满足的,即v(F)=1。对于公式F,如果每个子句最多只含3个变元,则称判断F的可满足性问题为3-SAT问题[4]。
称顶点集合V`(V`[?]V)为G的一个独立集,如果V`中任两顶点都不相邻接。称顶点集合K(K[?]V)为G的一个覆盖,如果G中每边至少有一端点在K中。顶点数最小的覆盖称为最小覆盖。G的最小覆盖的元素个数称为G的覆盖数。称顶点集S为G的团,如果G[S]为一完全图[3]。
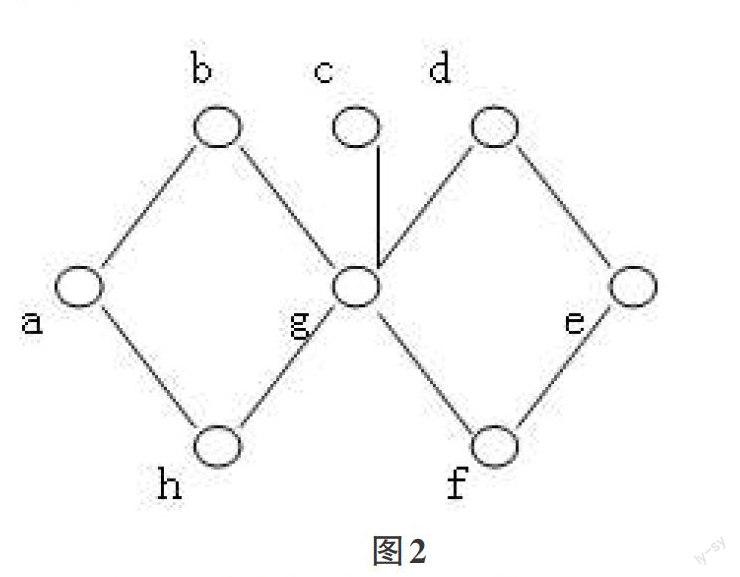
如果在图G的一个边子集M中,每条边的两端点不同,且任意两边不相邻,则称M为G的一个匹配(matching)。若边uv为M的一条边时,则称u与v在M下相匹配;称M-饱和(saturate)u(与v)。也称u(与v)为M饱和的[6]。类似地,可给出一顶点x为M-不饱和的定义。显然M的任一子集仍然是G的匹配。例如,图2所示的图中,边子集{ab,gh,ef},{cg,de},{ab}以及空集都是该图的匹配。
图2
如果G的每个顶点都是M-饱和的,则称M为图G的完美匹配[6]。显然,这时G的顶点数一定是偶数;且边导出子图G[M]是G的1-正则生成子图,称为G的1-因子(1-factor)。当然,顶点数为偶数的图也可能没有完美匹配,例如图2所示的图属于这种情况。称M为图G的最大匹配,如果对图的G的任一匹配M`都有|M`|≤|M|。例如图2中,边子集{ab,gh,ef}及{ab,cg,de}都是该图的最大匹配。显然,当G的最大匹配M不是完美匹配时,G中M不饱和顶点集是非空独立集。
称G中的路P为M-交错路(M-alternating path),如果P的边交替地属于M及E\M。如果M-交错路P的起点与终点都是M-不饱和的,称P为M-可扩路(M-augmenting path) [7]。
2 重要的结论
定理1:G为一个变量-子句图,M为G中的最大匹配,当且仅当G中不存在M-可扩路。
证明: [?]:假设G中有M-可扩路P,将P中M边与非M边进行交换,而其它M边不变,得新的匹配M`,且|M`|=|M|+1,这与M为最大匹配相矛盾。(其实上述运算就是:M`=M[Δ]E(P),其中[Δ]为集合对称差运算,即对任意两集合A与B有A[Δ]B=(A∪B)-(A∩B)。)
[?]:反正,假设M不是最大匹配,取G中任一最大匹配M*。令
H=G[M[Δ] M*]
则H中每个顶点至多与一条M的边及一条M*的边相关联,因此
dH(v)=1 or 2 [?]v∈V(H)
从而,H的每个分支都是一圈或路,由M及M*的边交错组成。但| M*|>|M|,H中一定有一分支是一条路P,且其起点和终点都是M*-饱和的。从而P是G中的M-可扩路,矛盾。
显然,对于一个变量-子句图,如果存在一个匹配,包含图中的所有子句顶点,那么,此图对应的公式一定可满足。
定理2:S为变量-子句图G的覆盖,当且仅当V\S为G的独立集。
证明:S为G的覆盖[?] 不存在两端点全在V\S中的边[?]V\S为G的独立集。
推论3:变量-子句图G,[β]为G的最小覆盖的元素个数,[α]为G的最大独立集的元素个数,[γ]为G的顶点个数,则[α]+[β]=[γ]。
证明:设S为G的最大独立集,则V\S为其覆盖,因此
[β]≤|V\S|=[γ]-[α]
又,设K为G的最小覆盖,则V\K为其独立集,因此
[α]≥|V\K|=[γ]-[β]
所以
[α]+[β]=[γ]
结论:S为G的最大独立集[?]V\S为G的最小覆盖。
关于图G中任一覆盖K及任一匹配M,由覆盖定义,M中每边至少有一端属于K,且匹配M中任两边无公共顶点,因此
|M|≤|K|
特别地,对G的最大匹配M*及最小覆盖K*有
| M*|≤| K*|
引理4:设M与K分别为G中的匹配与覆盖,如果
|M|=|K|
则M为最大匹配,K为最小覆盖。
证明:由|M|≤| M*|≤| K*|≤|K|得到。
定义1:对于一个二分图G=(X,Y,E),应满足什么条件才能有一个饱和X中每个顶点的匹配。称这种匹配为完全匹配。
称N(S)为S的邻集,指G中所有与S中顶点相邻接的顶点。一般而言,N(S)中也可能包含S中的顶点。
定理5:在变量-子句图[G=(X?A,E)]中,G包含使A中每个顶点都饱和的匹配
[?]|N(S)| ≥|S| [?]S[?]A
证明:[?]:假设G包含一个饱和A中所有顶点的匹配M,S为A的一个子集。因为在S中的顶点在M下匹配N(S)中的顶点,显然,有|N(S)| ≥|S|。
[?]:假设存在变量-子句图G,它满足条件|N(S)| ≥|S| 对于 [?]S[?]A,但不包含使A中每个顶点都饱和的匹配。令M*为G的最大匹配,u为A中M*-不饱和顶点。设
Z={v|[?]M*-交错(u,v)路}
由于M*为最大匹配,由定理1,Z-u中每个顶点都是M*-饱和的。令
S=Z∩A,T=Z∩X
则S\{u}与T的顶点在M*下相匹配。因此
|T|=|S|-1; N(S)[?]T
但我们有N(S)[?]T。故N(S)=T,由此得
|N(S)|=|T|=|S|-1<|S|
矛盾。
结论:如果公式F对应的变量-子句图[G=(X?A,E)]有完全匹配M,那么公式F一定可满足。
例2.1:对于例1.1中的公式F,对应的变量-子句图[G=(X?A,E)],有完全匹配M,假设M={(a,1),(b,2),(c,3),(d,4)},容易验证,公式F是可满足的。
推论6:对于一个k-CNF公式F对应的变量-子句图[G=(X?A,E)],如果G是一个k-正则图,则公式F一定可满足。
证明:由于k|A|=|E|=k|X|,所以|X|=|A|。
又,对任意S[?]A,令E1和E2分别为S和N(S)相关联的边集。E1[?] E2,所以
k|S|=|E1|≤|E2|=k|N(S)|,有|S|≤|N(S)| 对于[?]S[?]A
根据定理5,图G包含完全匹配,因此公式F可满足。
例2.2:一个3-CNF公式F={(x1[∨]x2[∨]x3),([?]x1[∨]x2[∨][?]x3),(x1[∨][?]x2[∨][?]x3)}
显然,对应的变量-子句图是一个3-正则图,公式F对应的图G有完全匹配,根据推论6,公式F可满足。
3 求解可满足性问题的算法
定义:在一个变量-子句图[G=(X?A,E)]中,称M为G最优匹配,如果M为G完美匹配,并且边的权值和[w(M)]=[e∈Mw(e)]为最大(或最小)[8]。
称X∪Y上定义的实函数[l]为可行顶点标号(feasible vertex labeling,简记为f.v.l.),如果它满足
[l(x)+l(y)≥w(xy)] [?x∈X,y∈Y]
对任一权变量-子句图可行顶点标号总是存在的,例如下面就是一个可行顶点标号:
[l(x)=maxy∈Y{w(xy)}x∈Xl(y)=0y∈Y]
我们记[El={xy∈E|l(x)+l(y)=w(xy)}]
并称以[El]为边集的G的生成子图为相等子图(equality subgraph),记为[Gl]。
定理7:设变量-子句图[G=(X?A,E)]的可行顶点标号[l],使[Gl]含一完美匹配M*,则M*是G的最优匹配。
证明:显然,M*也是G的完美匹配,且
[w(M*)=e∈M*w(e)=v∈X?Al(v)]
但对G的任一完美匹配M有
[w(M)=e∈Mw(e)≤v∈X?Al(v)]
因此[w(M)≤w(M*)],即M*是G的最优匹配。
算法1:
(1)以任一匹配M作为开始;(可取M=[φ])
(2)若M饱和A中的每个顶点,停止(M为完美匹配,公式F可满足)。否则,取A中M-不饱和顶点u,令S←{u},T←[φ];
(3)若N(S)=T(无完美匹配)。转入求最大匹配;
(4)(此时有N(S)[?]T)取y∈N(S)\T。若y为M-饱和的,设yz∈M,则 S←S∪{z},T←T∪{y},并返回(2);否则(y为M-不饱和的),存在M可扩路P,令M←M[Δ]E(P),并返回(1);
(5)得到最大匹配后,用最大匹配中的变量去化简公式,设X*={x|x是M-饱和的变量顶点},A*={a|a是M-饱和的子句顶点},X**={x|x是M-不饱和的变量顶点},A**={a|a是M-不饱和的子句顶点},如果满足
x∈X*,[?]a∈A**,(x,a)∈E (注意:变量x代表的文字必须是一致的)
那么
A*←A*∪{a},A**←A**\{a}
(6)若满足|A*|=|A|,则输出公式满足;否则,输出不满足;
下面是求解最优匹配算法的基本思想:任取一f.v.l.[l]作为开始。定[Gl],并在[Gl]上任取一匹配M作为开始的匹配。算法在非赋权图[Gl]上找完美匹配。若找到,它就是G的最优匹配;否则算法停止于某非完美匹配Mn及一Mn-交错树H,在[Gl]中它不能再生长(即[NGl(S)=T])。将[l]适当修改成新的f.v.l.[l`],使[Gl`]仍包含Mn及H,且H在[Gl`]中又可继续生长(即[NGl`(S)?T])。为此只要取[al=minx∈Sy?T{l(x)+l(y)-w(xy)}],并把S中每个顶点的标号都减少[al];把T每个顶点标号都增加[al]即可。重复上述过程,直到在某个[Gl]中找到完美匹配为止,它就是所求的最优匹配。
算法2:
以任f.v.l.[l]作为开始。定[Gl],并在[Gl]任取一匹配M(可为[φ])作为开始的匹配。
(1)若M饱和A的每个顶点,则M为最优匹配,停止;否则,任取一M-不饱和顶点u,令S←{u},T←[φ];
(2)若[NGl(S)=T],计算
[al=minx∈Sy?T{l(x)+l(y)-w(xy)}]
及新的f.v.l.[l`]
[l`(v)=l(v)-alv∈Sl(v)+alv∈Tl(v)其他]
并令[l←l`],[Gl←Gl`];
(3)(此时有[NGl(S)?T])选取[y∈NGl(S)\T],若y为M-饱和的,设yx∈M,作
S←S∪{x},T←T∪{y}
并返回到(2);否则,令P为[Gl]中的M-可扩-(u,y)路,令
M←M[Δ]E(P)
并返回到(1);
上述算法中的权值,代表变量-子句图中变量顶点的度数。
4 结束语
利用最大匹配规则求解因子图上的信息传播算法的收敛性作为信息传播算法收敛性的一个新的研究方法,主要是基于实例结构限制下的信息传播算法的收敛性分析。这对于实际应用中的信息传播算法的设计具有指导意义,希望能够得出一些具体结果,丰富信息传播算法的理论及算法研究。
参考文献:
[1] Heskes T. On the uniqueness of loopy belief propagation fixed points. Neural Computation, 2004,16:2379-2413.
[2] Ihler A T. Loopy belief propagation: Convergence and effects of message errors. Machine Learning Research, 2005,6:905-936.
[3] Mooij J M, Kappen H J. Sufficient conditions for convergence of the sum-product algorithm. IEEE Transactions on Information Theory, 2007,53:4422-4437.
[4] Shi X Q, Schonfeld D, Tuninetti D. Message error analysis of loopy belief propagation for the sum-product algorithm. Computer and Information Science, 2010, 1009:1-30.
[5] Feige U, Mossel E, Vilenchik D. Complete convergence of message passing algorithms for some satisfiability problems.Theory of computing, 2013,9(19):617-651.
[6] Brunsch T, Cornelissen K, Manthey B, Roglin H. Smoothed analysis of BP for minimum cost flow and matching. Journal of Graph Algorithms and Applications, 2013,17(6):647- 670.
[7] Norshams N, Wainwright M.J. Stochastic belief propagation: A low complexity alternative to the sum product algorithm. IEEE Transactions on Information Theory, 2013,59(4):1981-2000.
[8] Bollobas B. Random graphs, 2nd edn. Cambridge University Press, Cambridge,2001.

