基于计算流体力学技术的橙汁高温灭菌模型优化

顾超恒，陶乐仁，王金锋，陈娟娟，崔振科

（1.上海理工大学制冷与低温研究所，上海200093；2.上海海洋大学食品学院，上海201306）

基于计算流体力学技术的橙汁高温灭菌模型优化

顾超恒1，陶乐仁1，王金锋2，陈娟娟1，崔振科1

（1.上海理工大学制冷与低温研究所，上海200093；2.上海海洋大学食品学院，上海201306）

通过7组实验，采集了在恒温水（油）浴中加热模型罐时，模型罐内橙汁温度随时间的变化。通过数值传热方法进行模拟计算，将实验数据与模拟数据进行比较，验证模拟计算的可靠性与合理性。为了减少实际温度变化与模拟温度变化的误差，拟合出一条公式，通过UDF编程导入Fluent，完善Fluent中的模型，以适应罐装橙汁加热灭菌。在误差要求小于9.5%的情况下，橙汁加热灭菌在80℃～120℃之间，都可使使用本模型进行模拟计算。

果汁；灭菌工艺；流体动力学（CFD）；相似理论；热灭菌

果汁的加热灭菌工艺是指以80℃～150℃的温度加热果汁的灭菌模型以杀死果汁中的大肠杆菌、李斯特菌、金黄色葡萄球菌等致病菌和有害菌种的灭菌方法［1］。常见的加热灭菌方式有3种，为巴氏灭菌法、高温短时灭菌（HTST）、超高温瞬时灭菌（UHT）。其中巴氏杀菌是一种较温和的热杀菌形式，处理温度通常在80℃～100℃之间。高温短时杀菌是利用高温使微生物的蛋白质及酶发生凝固或变性而死亡的杀菌形式，处理温度通常在100℃～135℃之间。超高温瞬时杀菌的温度一般在135℃～150℃，杀菌时间为数秒［2］。本研究通过相似性理论与量纲分析原理，以工业中使用的灭菌罐，等比例缩小成模型罐，以便于实验研究。在同类现象相似的条件下，满足两者无量纲数雷诺数（Re），普朗特数（Pr）等相等，因此可以认为模型罐中温度场分布与实际用于工业灭菌的罐内温度场分布是相似的［3-5］。由于实验要受到实验周期、实验成本、采集仪器易老化等的影响，本研究在实验的基础上，利用计算流体力学来做对比，以找出合理的模拟模型，以便以后可以使用模拟计算来代替实验。其中，计算流体力学（computational fluid dynamics，CFD）是基于计算机技术的一种数值计算仿真工具，是用于求解流体的流动和传热问题［6］。模拟计算与实验相比，具有成本低，周期快，可以全面真实的反映出模型内部温度场、压力场、流场的变化情况，以便于问题的分析。因此，引入数值计算技术来代替实验是非常可行方便的方法［7-10］。但是，在模拟计算中，我们所使用的模型都是前人根据实验所得到的经验性公式，用于本实验中可能会产生一定的误差。因此，为了模拟计算能够更好地应用于果汁加热灭菌中，本研究通过实验所得数据与模拟结果相对比，以完善模拟所用模型。

1　实验装置与设备

实验设备主要部件有：数据采集计算机，恒温水（油）浴（CH1506），模型罐，Fluke-NETDAQ32（多点温度采集仪），如图1所示。

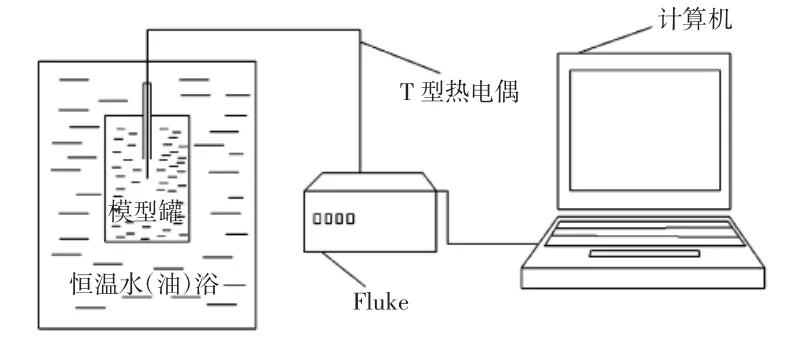
图1　实验装置图Fig.1Experimental setup

实验对象：新鲜橙汁。

橙汁的物性参数详细参照文献［11-12］定义：ρ= 1 026 kg/m，Cp=3 880 J/（kg·K），导热系数λ＝0.596 W/（m·K），对流换热系数［13］为h＝600 W/（m2·K）［14］。

用于实验的模型罐高为H=8cm，半径为R=2.5cm。

2　CFD模拟及理论分析

2.1模型建立及相应控制方程

本研究使用数值传热方法对研究对象进行传热分析，随着罐内液体温度的上升，液体会产生温度梯度从而会产生涡流，产生的速度会对罐内传热加强，因此罐内传热不单是导热也伴有对流现象的发生。根据实验所得数据分析，在加热初期罐内以导热为主，随着涡流的产生伴随着对流换热。因此，在模拟中，本研究选取laminar模型与标准k-ε模型相结合的形式进行模拟来验证模拟的方法是适合来做橙汁加热计算的。

2.1.1湍流动能方程

在标准k-ε模型的方程中，湍流动能方程如下。

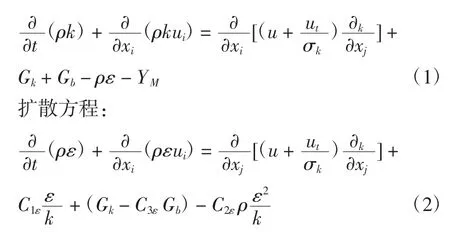
式中：Gk表示由层流速度梯度而产生的湍流动能；Gb是由浮力产生的湍流动能；YM是在可压缩湍流中，过渡的扩散产生的波动；C1，C2，C3是模型常量；σk和σe是k-ε方程的湍流Prandtl数。

2.1.2湍流速度模型

湍流速度ut由下式确定

式中：Cu为常数。

2.1.3模型常量

这些常量是从试验中得来的，包括空气、水的基本湍流以便更好地处理束缚和自由剪切流。虽然这些常量对于大多数情况是适用的，但为了更加符合实验数据减少误差，将在模拟中使用待定系数法来修改模型常量［15-17］。

为了使实验数据得以进行理论计算，在本研究中提出了以下假设：

1）模型罐壁面温度恒定，橙汁在恒壁温的情况下被加热；

2）在初始情况下，橙汁温度均匀一定且各向同性；

3）橙汁在加热过程中，物性参数保持不变。

2.2模型仓的3D建模

本研究模拟采用Gambit2.2.30以模型罐尺寸H= 8 cm，R=2.5 cm为原型建模。为了更好地反映出模型罐内部各点温度的变化，建模出3-D罐装图如图2所示。

图2　3-D罐模型及网格划分Fig.2Modeling and meshing of the three-dimensional can

采用interval size为0.5划分网格，并且设置此立体的3个面为wall，罐内液体物性参数根据橙汁参数来设置。使用Fluent6.2.16中三维计算器导入模型，选择合适的模型，根据实验数据设置边界条件和初始参数进行模拟计算。

2.3数值模拟及相关分析

根据实验数据，通过待定系数法，随着时间的不同修改模型常数Cmu值，可以得出Cmu与时间的一个函数关系即：Cmu=-0.857 1t2+13.443t+3.9。利用UDF编程，导入Fluent完善模型后，再次进行实验与模拟的对比，以证明方法的可实施性。图3～图9为实验与模拟中冷点温度的对比情况，通过对比我们可以得出，在修改了模型常数Cmu的情况下，模拟模型罐内温度变化是与实际相符的。

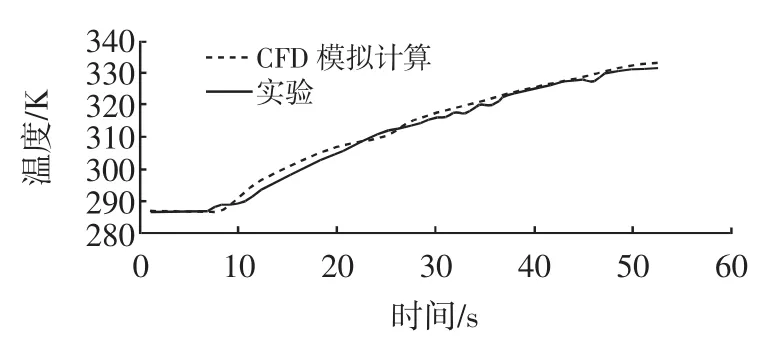
图3　壁面温度80℃时模型罐冷点温度随时间的变化Fig.3Temporal evolution of the cold point temperature of model can at a wall temperature of 80℃

从图3可以看出在0 s～9 s之间，冷点［18］温度基本变化不大，10 s～45 s左右时，冷点温度变化明显，这是因为内外传热温差大及对流取代导热占主导地位，46 s以后，冷点温度变化率减小，这是因为内外温差随着罐内温度的升高而逐渐减小，使得传热减弱。

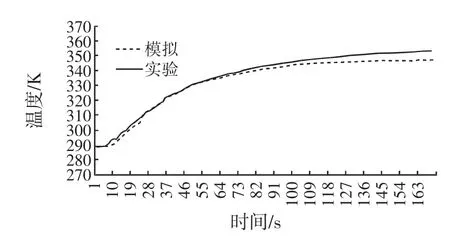
图4　壁面温度85℃时模型罐冷点温度随时间的变化Fig.4Temporal evolution of the cold point temperature of model can at a wall temperature of 85℃

从图4可以看出在0 s～11 s之间，冷点温度基本变化不大，12 s～110s左右时，冷点温度变化明显，这是因为内外传热温差大及对流取代导热占主导地位，111 s以后，冷点温度变化率减小，基本上已经趋于水平，可见传热很小，这是因为内外温差随着罐内温度的升高而逐渐减小，使得传热减弱。

图5　壁面温度88℃时模型罐冷点温度随时间的变化Fig.5Temporal evolution of the cold point temperature of model can at a wall temperature of 88℃

从图5可以看出在0 s～14 s之间，冷点温度基本变化不大，15 s～120 s左右时，冷点温度变化明显，这是因为内外传热温差大及对流取代导热占主导地位，121 s以后，冷点温度变化率减小，基本上已经趋于水平，可见传热很小，这是因为内外温差随着罐内温度的升高而逐渐减小，使得传热减弱。

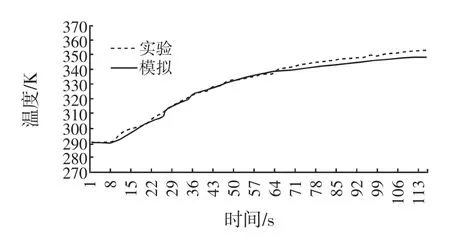
图6　壁面温度90℃时模型罐冷点温度随时间的变化Fig.6Temporal evolution of the cold point temperature of model can at a wall temperature of 90℃

从图6可以看出在0 s～16 s之间，冷点温度基本变化不大，17 s～80 s左右时，冷点温度变化明显，这是因为内外传热温差大及对流取代导热占主导地位，81 s以后，冷点温度变化率减小，这是因为内外温差随着罐内温度的升高而逐渐减小，使得传热减弱。

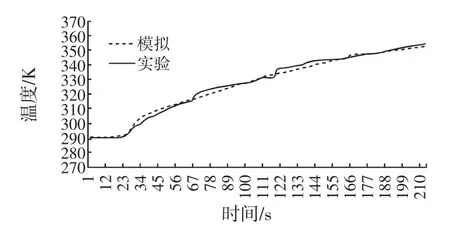
图7　壁面温度100℃时模型罐冷点温度随时间的变化Fig.7Temporal evolution of the cold point temperature of model can at a wall temperature of 100℃

从图7可以看出在0 s～16 s之间，冷点温度基本变化不大，17 s以后，冷点温度变化明显，这是因为内外传热温差大及对流取代导热占主导地位，但是随着模型罐处于恒温水（油）浴的时间增加，可以看出其温度的变化率是减小的，可见，内外温差减小是影响传热的关键因素。

图8　壁面温度110℃时模型罐冷点温度随时间的变化Fig.8Temporal evolution of the cold point temperature of model can at a wall temperature of 110℃

从图8可以看出在0 s～15 s之间，冷点温度基本变化不大，16 s以后，冷点温度变化明显，这是因为内外传热温差大及对流取代导热占主导地位，但是随着模型罐处于恒温水（油）浴的时间增加，可以看出其温度的变化率是减小的。

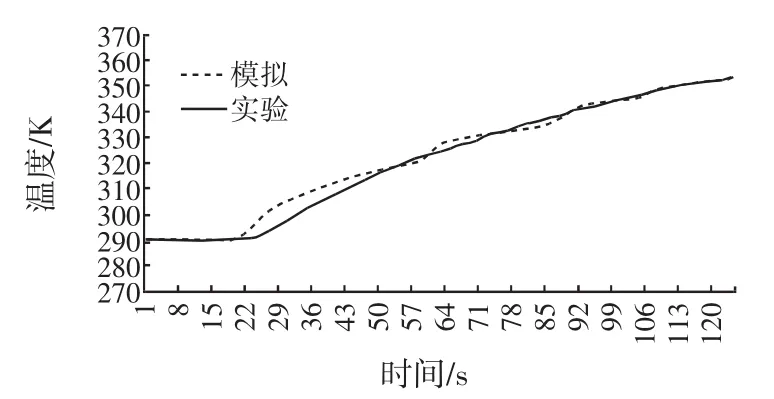
图9　壁面温度120℃时模型罐冷点温度随时间的变化Fig.9Temporal evolution of the cold point temperature of model can at a wall temperature of 120℃

从图9可以看出在0 s～20 s之间，冷点温度基本变化不大，21 s以后，冷点温度变化明显，这是因为内外传热温差大及对流取代导热占主导地位，但是随着模型罐处于恒温水（油）浴的时间增加，可以看出其温度的变化率是减小的。

由图3～图9可以看出，模拟数据与实验数据随着时间的变化，在相同时刻相差微小，误差基本上可以保持在9.5%以内［19～20］，甚至更小，从而确保了模拟计算在果汁加热灭菌中是可以使用的。同时，虽然恒温水域的温度不同，但是果汁在加热中变化趋势基本相同。在初始时刻，罐内温度基本没有变化，一方面是由于热电偶测得是模型罐中心温度也即其冷点温度还没有传到，另外也可以看出初始时刻罐内传热主要以导热为主，随着时间的增加对流渐渐处于主导地位。

3　结论

本研究通过实验与模拟相结合，完善了模拟中的计算模型，推导出Cmu与时间的一个函数关系即：Cmu= -0.857 1t2+13.443t+3.9。并且，再次通过实验验证，实验数据与模拟数据误差在9.5%以内，耦合情况非常好。可见，拟合出来的公式在果汁的加热中是可以应用的。另外，从实验中可以看出，在壁面温度一定的情况下，模拟罐加热在初期和后期效果都不太明显，为了更好地减少能源消耗，可以先通过模拟找出合理的加热时间与加热温度。同时，为了更好地考虑节能型，也可以尝试改变模型罐的形状，通过模拟找出最节能的模型罐，从而来优化设计。

［1］谢晶，汤毅，王金锋，等.基于CFD技术的橙汁高温短时灭菌后冷却工艺优化［J］.食品科学，2013，34（10）：77-81

［2］仇农学，罗仓学，易建华.现代果汁加工技术与设备［M］.北京：化学工业出版社，2006：45-51

［3］杨世铭，陶文铨.传热学［M］.北京：高等教育出版社，2006：230-236

［4］山东工学院，东北电力学院.工程流体力学［M］．水利电力出版社，1979：138-147

［5］张淑红，陶乐仁，郑志皋，等.机械通风粮仓冷却效果的模型实验研究［J］.湖南农业科学，2011（7）：101-103

［6］李万平.计算流体力学［M］.武汉：华中科技大学出版社，2004：4-17

［7］VARMA M N，KANNAN A.Enhanced food sterilization through inclination of the container walls and geometry modifications［J］.International Journal of Heat and Mass Transfer，2005，48（18）：3752-3762

［8］VARMA M N，KANNAN A.CFD studies on natural convective heating of canned food in conical and cylindrical containers［J］. Journal of Food Engineering，2006，77（4）：1024-1036

［9］A G Abdul Ghani，M M Farid a，X D Chen，P.Richards，An investigation of deactivation of bacteria in a canned liquid food during sterilization using computationaluid dynamics（CFD）［M］.Journal of Food Engineering，1999

［10］Kai Knoerzer，Roman Buckowa，Belinda Chapman，Pablo Juliano，Cornelis Versteeg，Carrier optimisation in a pilot-scale high pressure sterilisation plant-An iterative CFD approach employing an integrated temperature distributor（ITD）［M］.Journal of Food Engineering，2010

［11］POMERANZ Y.Functional properties of food components［M］.Orlando，Fla，USA：Acadenic Press，1985：417-422

［12］Mc WILLIAMS M.Food fundamentals［M］.New York：John Wiley &Sons，Inc，1979：554-555

［13］ABDUL-GHANI A G，FARID M M，CHEN X D.A computational and experimental study of heating and cooling cycles during thermal sterilization of liquid foods in pouches using CFD［J］.Journal of Process Mechanical Engineering，2003，217（1）：1-9

［14］王金锋，谢晶，汤毅，等.基于计算流体力学技术的橙汁超高温瞬时灭菌工艺优化［J］.2012，33（16）：30-34

［15］韩占忠，王敬，兰小平.流体工程仿真计算实例与应用［M］.北京：北京理工大学出版社，2004

［16］温正，石良辰，任毅如．FLUENT流体计算应用教程［M］.北京：清华大学出版社，2009

［17］朱红钧，林元华，谢龙汉.FLUENT流体分析及仿真实用教程［M］.北京：人民邮电出版社，2010

［18］刘建学，纵伟.食品保藏原理［M］.南京：东南大学出版社，2006：128-138

［19］王金峰，汤毅，谢晶，等.灌装橙汁超高温瞬时灭菌的数值模拟研究［J］.工程热物理学报，2012，33（2）：288-290

［20］谢晶，汤毅，王金锋，等.基于CFD技术的橙汁高温短时灭菌后冷却工艺优化［J］.食品工业科技，2013，34（10）：77-81

Optimization of High-temperature Sterilization of Orange Juice Based on Computational Fluid Dynamics（CFD）

GU Chao-heng1，TAO Le-ren1，WANG Jin-feng2，CHEN Juan-juan1，CUI Zhen-ke1
（1.School of Energy and Power Engineering，University of Shanghai for Science and Technology，Shanghai 200093，China；2.College of Food Science and Technology，Shanghai Ocean University，Shanghai 201306，China）

In this study，seven groups of experiments are used to collect in constant temperature water（oil）in the heating bath tank model，the model juice tank temperature changes with time.To simulation by numerical heat transfer，the experimental data are compared with the simulated data to verify the reliability and rationality. In order to reduce the actual temperature error with simulation's temperature，fit out a formula，import fluent by UDF programming and make Fluent's model perfect to adapt to heat-sterilized canned orange juice.In the case of the error less than 9.5%，the model can be used in the orange heat sterilization at between 80℃-120℃.

juice；Sterilization process；CFD；Similarity theory；thermal sterilization

10.3969/j.issn.1005-6521.2015.13.018

2014-04-06

顾超恒（1988—），男（汉），在读研究生，研究方向：制冷与低温工程。