基于变形焦炭塔的冷点处套合应力分析

林 萍，杨森皓，王增超，银建中，韩志远，谢国山，徐君臣

(1.大连理工大学 化工学院，辽宁大连 116024；2.中国特种设备检测研究院,北京 100029； 3.惠生工程(中国)有限公司，上海 201210)

0 引言

焦炭塔作为延迟焦化工艺中的核心反应器，是典型的复杂热循环承载设备[1]。通常情况下，焦炭塔工作温度在室温到480 ℃之间循环变化，包括预热、生焦、冷却、除焦4个主要阶段。每个工作周期，焦炭塔承受内压与循环温度载荷的共同作用。在焦炭塔服役多年后，塔体出现不同程度的鼓胀，变形后的焦炭塔直径会有明显改变，影响焦炭塔的寿命计算与安全评估[2]。

近年来，激光扫描技术被应用于焦炭塔鼓胀过程的跟踪[3]，得到变形后焦炭塔模型。ARAQUE等[4]通过对激光扫描所得三种不同角度下的变形曲线的分析，确定凸起和裂纹的位置，建立了“之”字形模型和尖角模型。SAMMAN[5-6]采用线弹性有限元模型，研究压力容器在内压载荷作用下，凸起变形尺寸和形状对轴向和周向应力的影响，并从激光扫描数据库中确定9种凸起模型，将其成因与工艺、加载形式等相联系。VIVAS等[7-8]经过激光扫描得到变形焦炭塔模型，应用热-结构顺序耦合法建立有限元模型，计算瞬态温度和应力分布。王增超[9]应用动态坐标系法对两个变形较大区域进行了热力耦合分析，并且与理想几何结构的应力和应变进行比较。

继低周热机械疲劳损伤[10]之后，焦炭与塔壁套合效应[1]被认为是焦炭塔鼓胀变形的另一重要因素。工程实际中，塔内壁生成的焦炭，在水冷阶段会阻碍塔壁的轴向和周向收缩，形成套合效应，加剧塔体鼓凸变形。陈孙艺[11-12]提出了塔体变形与不均匀变化的焦炭温度场之间的关系，讨论了焦炭对塔体的阻碍作用在轴向和周向的区别。朱成诚等[13]对焦炭塔的下部筒节与锥形封头处进行套合效应有限元模拟计算，表明套合效应是引起塔体鼓胀的决定性因素之一。SAMMAN等[5，14]也多次提及焦炭塔鼓胀变形是焦炭与塔体母材相互作用的结果。然而，目前国内外对于套合效应的研究中，焦炭模型多选用轴对称的中心通道模型[15]，而非更接近实际生产状况的树枝状通道模型[16]，这种模型更有利于研究冷点的作用。

陈孙艺[17]基于工程实际情况，提出热斑概念并建立了三种计算模型。OKA等[14]选取鼓胀点中最恶劣的操作温度进行应力分析，认为冷热点的作用是塔体出现永久变形的主要原因。ZHANG等[18-19]为焦炭塔局部应力计算(冷点和热点)提供了简化理论模型。JU等[20]研究发现冷点的存在会导致塔壁出现严重的局部弯曲。王增超等[21]对变形较大的两个区域施加冷点作用，并将结果与未变形的焦炭塔模型进行了比较。但是，以上关于冷点的研究均忽略了水冷阶段焦炭与塔壁套合效应的影响。

本文基于有限元软件，应用热-结构顺序耦合法，采用生死单元技术对焦炭塔局部冷点处的套合应力进行有限元计算研究。应用在役焦炭塔经激光扫描所得相关模型及数据，考虑实际工况中温度场的变化；考虑焦炭在水冷阶段的套合效应；考虑冷却水沿树枝状通道进入塔壁，形成冷点，先于焦炭覆盖位置冷却。分别对两个变形较大的区域(A区、B区)和未变形模型建立有焦炭的冷点处套合模型和无焦炭冷点模型，研究变形对于冷点套合模型和冷点无焦模型的影响，再分析同变形下套合对冷点的作用效果；最后考虑冷却水温度、两冷点排列方式和两点间距离对应力的影响。

1 计算模型和材料物性

1.1 计算模型

以某炼油厂服役22年的焦炭塔为研究对象，该焦炭塔设计高度28.65 m，内径6.1 m，顶端球形封头，下端锥形封头，对所得激光扫描数据进行逆向分析后,得到的有限元计算模型见图1，变形主要集中在第2，3筒节和第6筒节的上方，其他位置几乎无变形。在这两个变形较大区域截取冷点套合模型计算区域，从上到下分别命名为A区和B区，为方便结果对比，建立直径为6.1 m，厚度为34 mm的未变形焦炭塔理想筒体模型。

图1 变形焦炭塔有限元计算模型Fig.1 FEM model of deformed coke drum

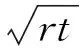
(1)

由圣维南原理可知：冷点作用产生的应力会影响其四周局部范围的应力分布，故以冷点中心为圆心，向外扩展直径为1 000 mm的圆环区域作为冷点周围部分，分析时选择冷点及这个圆环部分。由于结构计算中需要对边界施加约束和载荷，为避免端部约束对冷点及其周围计算结果产生影响，模型高度、宽度均需远大于冷点及其周围部分，此处高度和宽度均为4 000 mm[21]。将模型在DM中对除冷点外区域进行焦炭填充，建立直通冷点的通道，来模拟冷点局部树枝状通道模型。后进行slice切割，为后续网格划分和按路径提取应力结果做准备，处理后计算模型如图2所示。

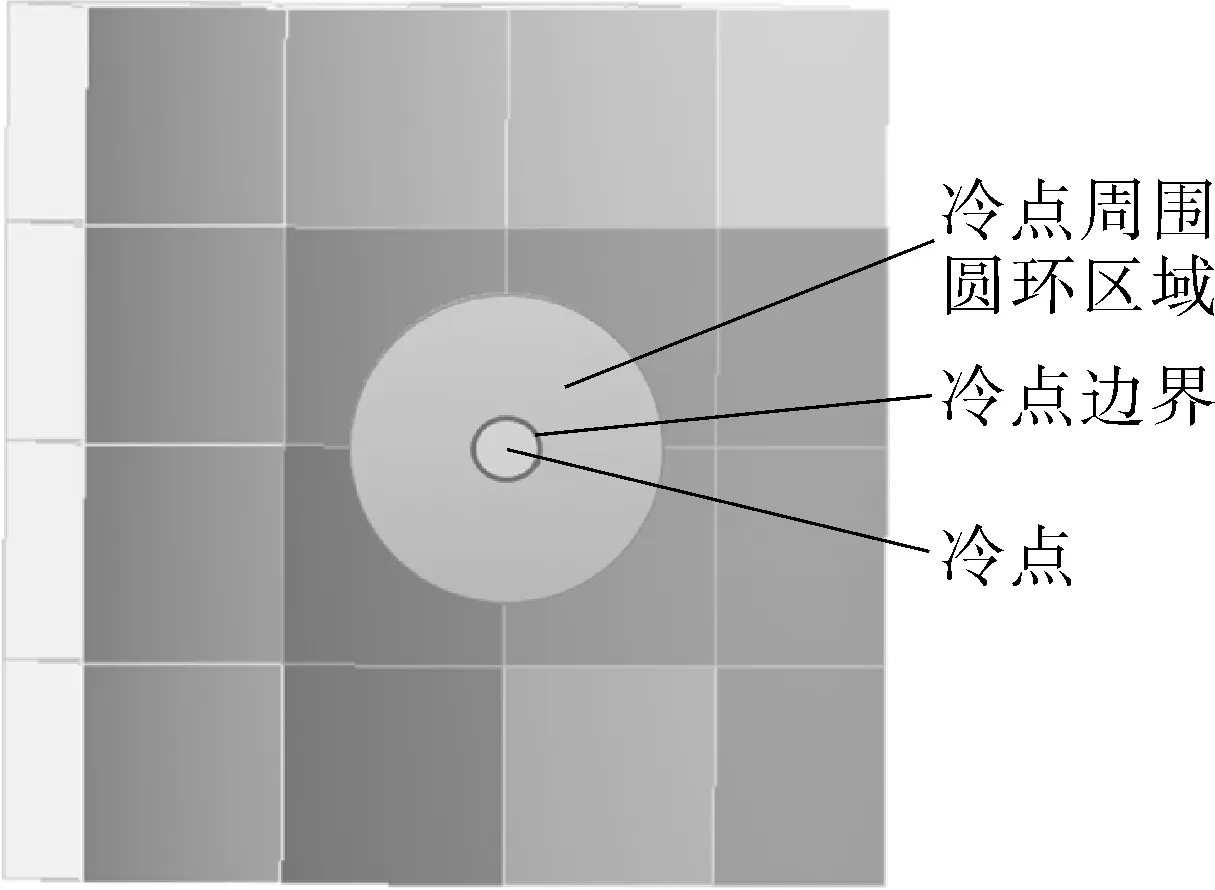
(b)冷点计算模型的外壁面图2 冷点计算模型Fig.2 Computational model of cold spot

1.2 材料物性

计算中应用热-结构顺序耦合法，首先进行温度场计算，将所得的温度场作为己知条件，以体载荷的形式施加到结构场中，进行热应力分析，得到应力应变场。瞬态温度场计算需定义导热系数、比热等与温度有关的材料属性，结构场需定义弹性模量等力学材料属性。本文焦炭塔主体材料为20g，其各项参数见表1[21]，工作中生成的焦炭物性参数见表2。

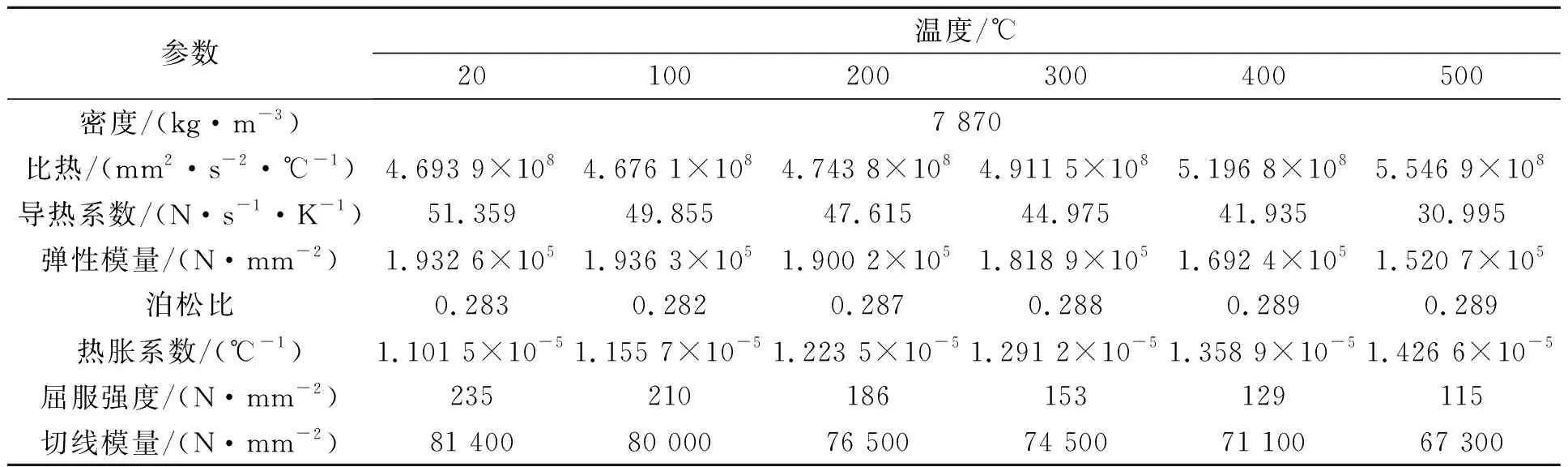
表1 20g(Q245R) 物性参数Tab.1 Material property parameters of 20g(Q245R)

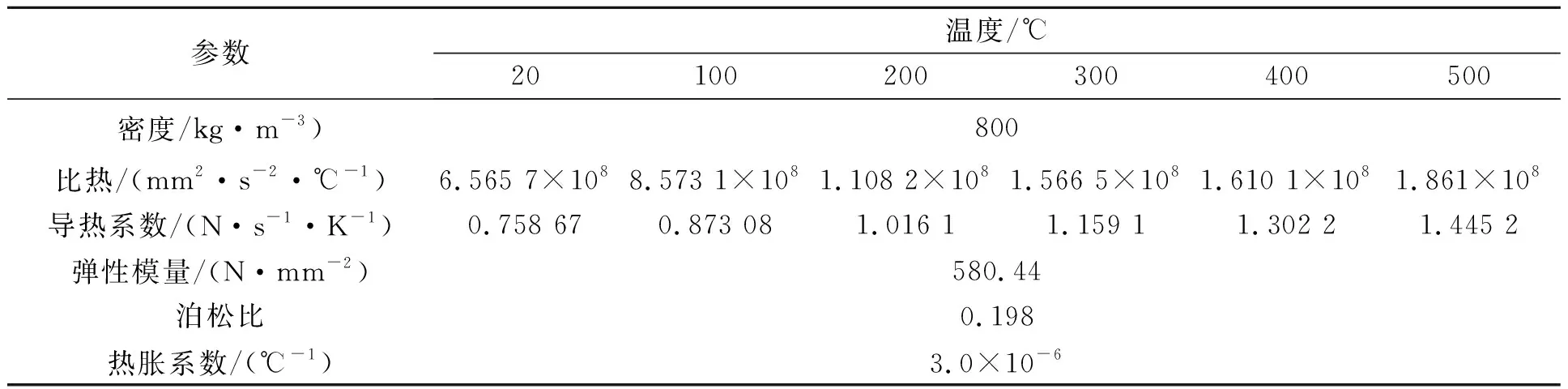
表2 焦炭物性参数Tab.2 Material property parameters of coke

2 有限元计算

2.1 网格划分

计算中涉及变形曲面模型，为了能更好地逼近结构的曲线和曲面边界，同时保证结构场运算速度，应用六面体高阶网格单元。在壁厚方向划分3层网格，对冷点及其周围部分进行局部加密处理，焦炭单元应用六面体扫掠网格，并在保证计算精度的前提下，网格划分尽可能大一点，以加快计算速度。由于软件中壳体默认为四面体网格，在网格划分时插入Hex Dominant Method命令，最终模型网格划分如图3(a)所示。在冷点内壁建立2条路径，A路径和B路径，为结果分析做准备，路径如图3(b)所示。

(a)网格划分

(b)两个路径图3 网格划分和两个路径Fig.3 Meshing and two paths

2.2 确定及施加温度场载荷

文中焦炭塔的工艺周期为42 h，包括预热、生焦、冷却、除焦等4个主要工艺阶段，主要工艺阶段持续时间如表3所示。

表3 焦炭塔主要工艺阶段持续时间Tab.3 Duration of main process stage of coke drum

根据焦炭塔实际工艺阶段，同时考虑冷点作用特点，低温冷却水进入塔内后，沿着树枝状通道迅速抵达塔壁，冷却塔壁的某个位置，而被冷却点的周围仍被焦炭包裹着，这样就产生了对塔体危害很大的冷点。分别对焦炭塔内壁的冷点内部和冷点外区域施加如图4所示的温度场。

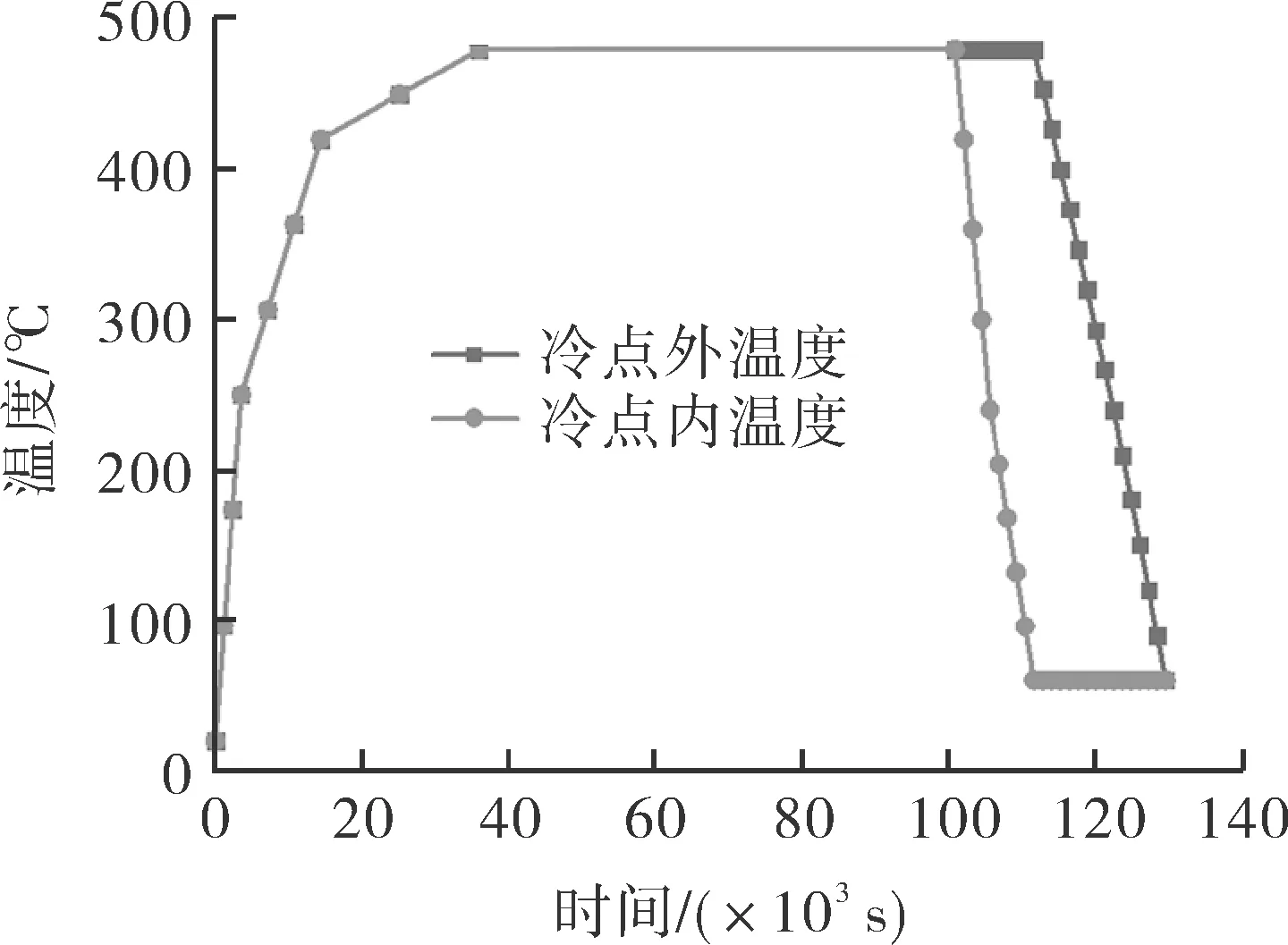
图4 冷点及其周围施加温度场曲线Fig.4 Applied temperature field histories of the cold spots and their surrounding areas

求解冷点及冷点外区域温度场，需已知初始温度和边界条件这两个初始条件，此处初始温度为20 ℃。塔内介质复杂，边界条件选用第三类边界条件，塔内介质温度和对流换热系数已知，此处对流换热系数为与实测值误差极小的模拟值(即等效对流换热系数)。第三类边界条件参数如表4所示。

表4 第三类边界条件参数Tab.4 The third kind of boundary condition parameters

塔体外壁覆盖保温层，忽略热量损耗，可看作绝热边界，其余部位也设置为绝热边界。焦炭单元的计算应用生死单元法，在温度场初始时刻“杀死”焦炭单元，生焦结束后“激活”焦炭单元，激活时焦炭设置480 ℃的初始温度。

2.3 结构载荷施加及边界条件

结构分析中，采用与瞬态热分析相同的有限元模型和网格[22-23]，将热分析得到的计算结果以体载荷形式施加到结构场模型，为防止模型刚性移动，对模型进行几何约束，上端面施加远端约束，下端面约束轴向移动，左右两侧面施加无摩擦对称约束，焦炭单元激活后，与塔壁同约束。焦炭塔工作周期内压力值很小且不同工况下变化不大，所以对塔内壁施加实际工作内压 0.158 MPa，在上端面施加轴向等效应力，方向向上。变形模型约束及载荷施加与未变形模型相同。

3 结果分析

3.1 温度场分析

3.1.1 冷点套合对内外壁温影响

在温度场计算中，未变形模型与A区、B区的温度场变化趋势相同，关于温度场内外壁温的分析，只以未变形模型为例，其余模型不再赘述。文中“冷点”、“冷点内”和“冷点区域”均指图2(b)中的冷点部分；“冷点外部”和“冷点周围区域”指图2(b)中的冷点周围圆环区域。

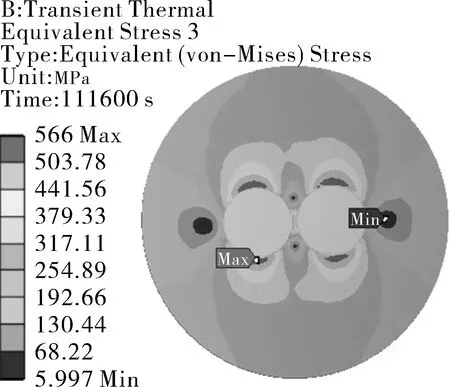
对模型施加如图4所示温度场，在第111 600 s时(给水冷却初期)，冷点与冷点周围区域温度梯度最大，此时冷点由于树状通道的存在已经冷却至最低温度，而冷点周围仍处在高温状态，冷点及其周围区域的内外壁温度场如图5所示，温度场以冷点为中心呈环状向四周辐射，内壁由于焦炭附着在冷点外区域，且由表1和表2可知焦炭的导热系数远小于塔壁主材，内壁在焦炭附着的影响下，冷点边缘区域温度下降较外壁缓慢，环状辐射没有外壁明显。

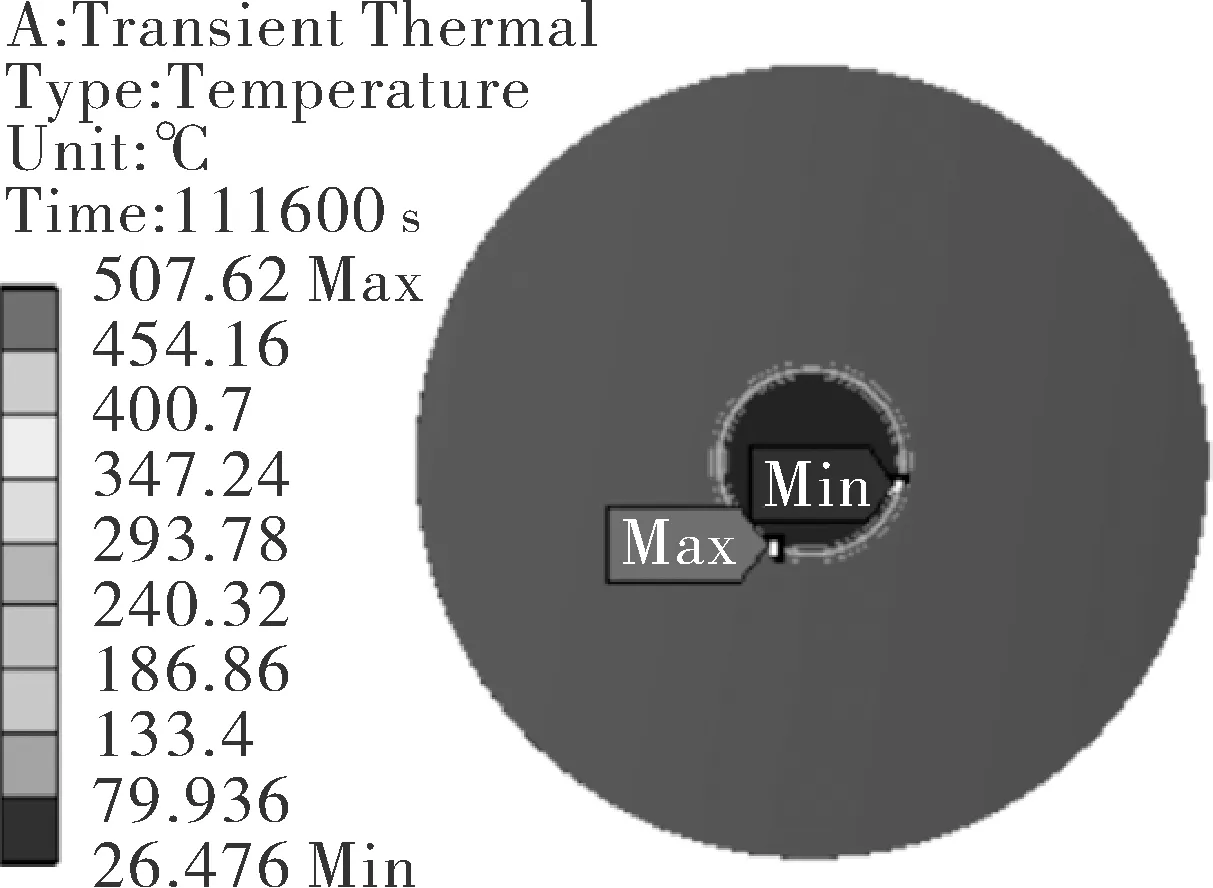
(a)内壁温度场

(b)外壁温度场图5 第111 600 s时的温度场Fig.5 Temperature field at the 111 600 s

为观测不同位置内外壁温差，分别在冷点内、冷点边界和冷点外部的内外壁分别提取1-1′，2-2′，3-3′这6组点如图6(a)所示，绘制温度变化曲线如图6(b)所示，图6(c)示出局部放大图。整个工作过程中，冷点内和冷点外部的内外壁温度都几乎重合，但在冷点边界处，水冷阶段内壁温度高于外壁温度。

图6 内外壁温度场曲线Fig.6 Temperature field curves of inner and outer walls

3.1.2 变形对冷点套合温度场的影响

对未变形和A区、B区冷点处套合模型沿图3(b)中A路径提取111 600 s时的温度场，绘制不同模型同路径、同时间下的温度曲线，如图7所示。此时冷点内已经开始水冷，而焦炭附着的套合区域尚未降温，在冷点边缘处会产生极大的温度梯度，此处温度出现大幅震荡，出现极大、极小值；在塔壁形变的影响下，A区和B区比未变形模型的温度波动大。

图7 三种模型沿A路径在111 600 s时的温度曲线Fig.7 Temperature curves of the three models along path A at 111 600 s

3.2 结构场分析

3.2.1 变形对冷点套合应力场的影响

分别对变形和未变形的冷点套合模型沿如图3(b)中A,B路径提取应力最大时刻111 600 s时的冷点及其周围筒壁的轴向和周向应力。

图8(a)(b)示出A路径周向应力，可以看出:(1)对于未变形模型，周向应力和轴向应力都关于冷点中心呈对称分布；而变形模型，受塔体形变影响，A区、B区应力分布不规则；B区在冷点内部的周向应力曲线呈不规则凸起状，大部分点的应力比未变形模型同一位置的应力大；A区在冷点内部的周向应力呈波动状，并且大部分点的应力比未变形模型同一位置的应力小；(2)3个模型周向应力都是在冷点内部受拉应力，冷点边缘处应力突变为负值，冷点边缘受压应力且为压应力最大值，随着逐渐远离冷点，路径上点受的压应力逐渐减小；(3)从周向应力局部放大图(见图8(b))可以看出，冷点下边缘(左侧谷值)周向应力A区>未变形>B区，上边缘(右侧谷值)为A区>B区>未变形。图8(c)为A路径轴向应力，未变形模型和B区都是冷点中心附近应力出现最大值，A区是冷点接近边界处应力最大，应力极值B区>未变形>A区，远离冷点应力逐渐减小，并逐渐趋于平稳。

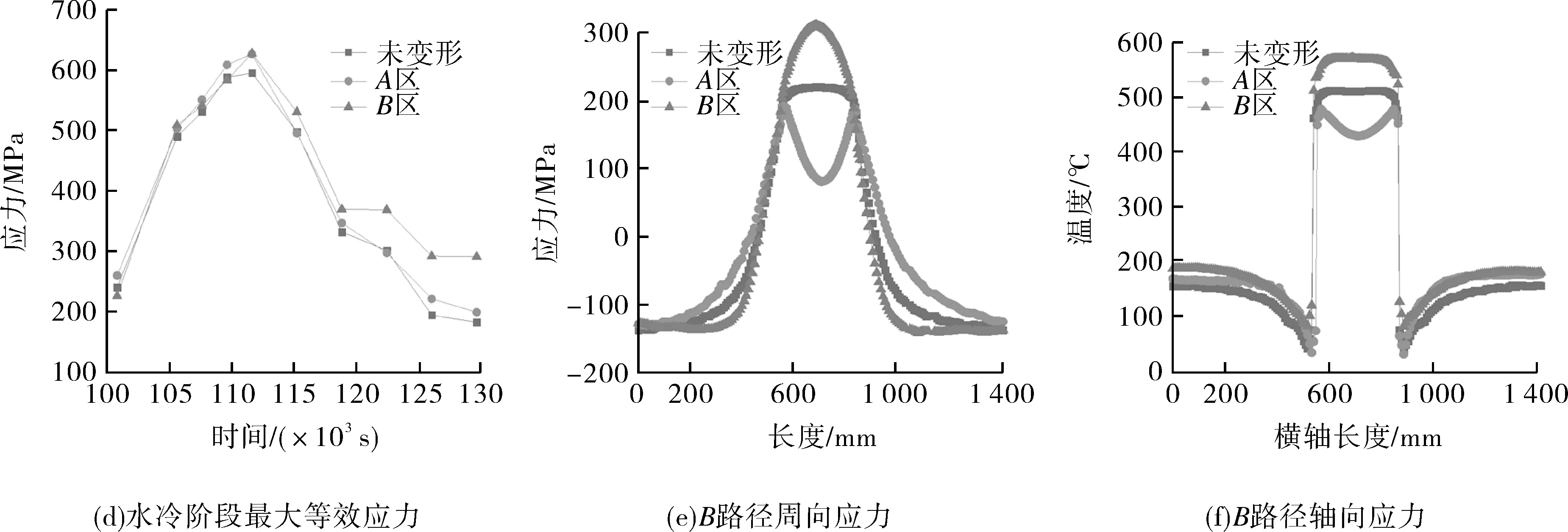
图8 按路径提取应力Fig.8 Stress extraction by path

图8(d)为冷点开始降温后，图6(a)中2点处水冷阶段最大等效应力曲线图，在应力云图中冷点上下边缘为最大等效应力处，左右边缘为最小等效应力处：(1)未变形最大等效应力为588.94 MPa，A区为625.7 MPa，B区为626 MPa。A区、B区的最大等效应力均大于未变形模型，A区、B区相较于未变形模型最大应力分别增加了6.23%和6.28%，但不同变形区域对最大等效应力影响不大，不同变形区域主要影响了应力的分布；(2)冷点套合后瞬时最大应力高达590～630 MPa，此时冷点及其边缘壁温在100 ℃左右，塔壁材料屈服强度为210 MPa，最大等效应力大于屈服应力，冷点的套合使得冷点边缘处塔壁开始进入屈服阶段，出现塑性变形，但由于此高应力是瞬态应力，而后随着冷点周围逐渐冷却，温度梯度减小，热应力降低，等效应力逐渐下降，并稳定在180～300 MPa;且此最大应力作用范围只在冷点边界极小范围处，只是局部进入塑性区；但是如果此位置在多次循环中受到高应力作用，可能出现裂纹，导致塔体失效。

图8(e)(f)为沿B路径提取轴向和周向应力，可以看出：(1)B路径的周向应力，冷点内受拉应力，从冷点边缘处开始随着与冷点距离的增加逐渐降低，最终变为压应力;(2)冷点边缘处轴向应力为负值，表明冷点左右边缘轴向受压，随着远离冷点，轴向应力逐渐恢复为拉应力;(3)B路径 3个模型的应力分布曲线都关于冷点中心呈对称状。

综上所述，冷点内周向受拉应力，冷点外周向受压应力，这是因为冷点内壁受冷收缩，在变形协调的影响下，冷点处产生阻碍收缩的拉应力，焦炭附着处的塔壁尚未冷却，塔壁周向受压。且从图中发现A路径上的冷点及其边界的轴向应力均大于周向，其原因是：(1)A路径的冷点上下边界周向均被焦炭覆盖，周向的收缩是双向、均匀的，因而摩擦力小，抵抗收缩的阻力小，故周向应力小;(2)此处的轴向方向上焦炭覆盖不均匀，且由于塔体轴向收缩是单向向下的[12]，收缩不均匀阻力大，所以轴向应力大。B路径同理。

3.2.2 套合对冷点处应力场的影响

分别对未变形、A区和B区的冷点模型建立无焦模型，得出各个时间的最大等效应力，如图9所示。未变形、A区、B区的无焦冷点最大等效应力分别为413.36，448.65，473.03 MPa。无焦时，相比未变形模型的最大等效应力，A区提升8.53%，B区提升14.44%。在同一变形下，对比套合前后最大等效应力，未变形模型提高42.5%，A区提高39.5%，B区提高30.9%。综上可知：(1)套合前后未变形模型最大等效应力变化最大；(2)无焦情况下，由变形所引起的冷点无焦最大等效应力增幅比套合之后应力增幅大。这是因为在无焦炭时，冷水到达冷点，塔壁直接收缩，变形后的模型收缩更不均匀、应力也更大；但是套合后，套合所产生的应力大，变形导致的应力作用效果看起来不明显，同时焦炭也对变形塔壁冷点处的收缩起到了阻碍作用。

图9 无焦模型等效应力Fig.9 Equivalent stress of the model without coke attached

3.3 影响因素

3.3.1 冷却水温

选择未变形模型和A区、B区模型，在冷却水温度分别为 40,60,80,100 ℃时，分析冷点附近Mises最大等效应力的变化，如图10所示。首先，无论对于变形模型还是未变形模型，焦炭塔的最大等效应力均随着冷却水温度的降低而升高；其次，A区、B区由于局部鼓胀变形的影响，对于相同的冷却水温度，变形模型的最大等效应力明显高于未变形模型，随水温变化趋势也更明显，其中A区应力随水温下降得最快。

图10 不同水温下的最大等效应力Fig.10 Maximum equivalent stress at different water temperatures

3.3.2 多冷点因素

生焦过程中，树枝状通道的生成具有随机性，会出现多个冷点距离很近的情况，多冷点共同作用下对应力结果产生一定的影响。以双冷点套合为例进行计算，首先考虑冷点的排列方式，如图11所示。单个冷点作用时冷点应力最大值位于冷点上下两端，所以两冷点竖直排列对应力值影响最大；水平排列时，虽然左右两端应力值有一定增加，但仍小于上下两端应力。

(a)竖直排列

(b)水平排列图11 多冷点排列Fig.11 Arrangement of two cold spots

考虑竖直排列的两冷点圆心间的距离对应力影响，如图12所示。A区等效应力明显比未变形应力大，且在两冷点距离较近时，A区应力下降更快，距离变远时，下降缓慢；B区比未变形应力大一些，但不明显，在两冷点距离较近时，B区应力下降更快，距离变远时，下降缓慢。

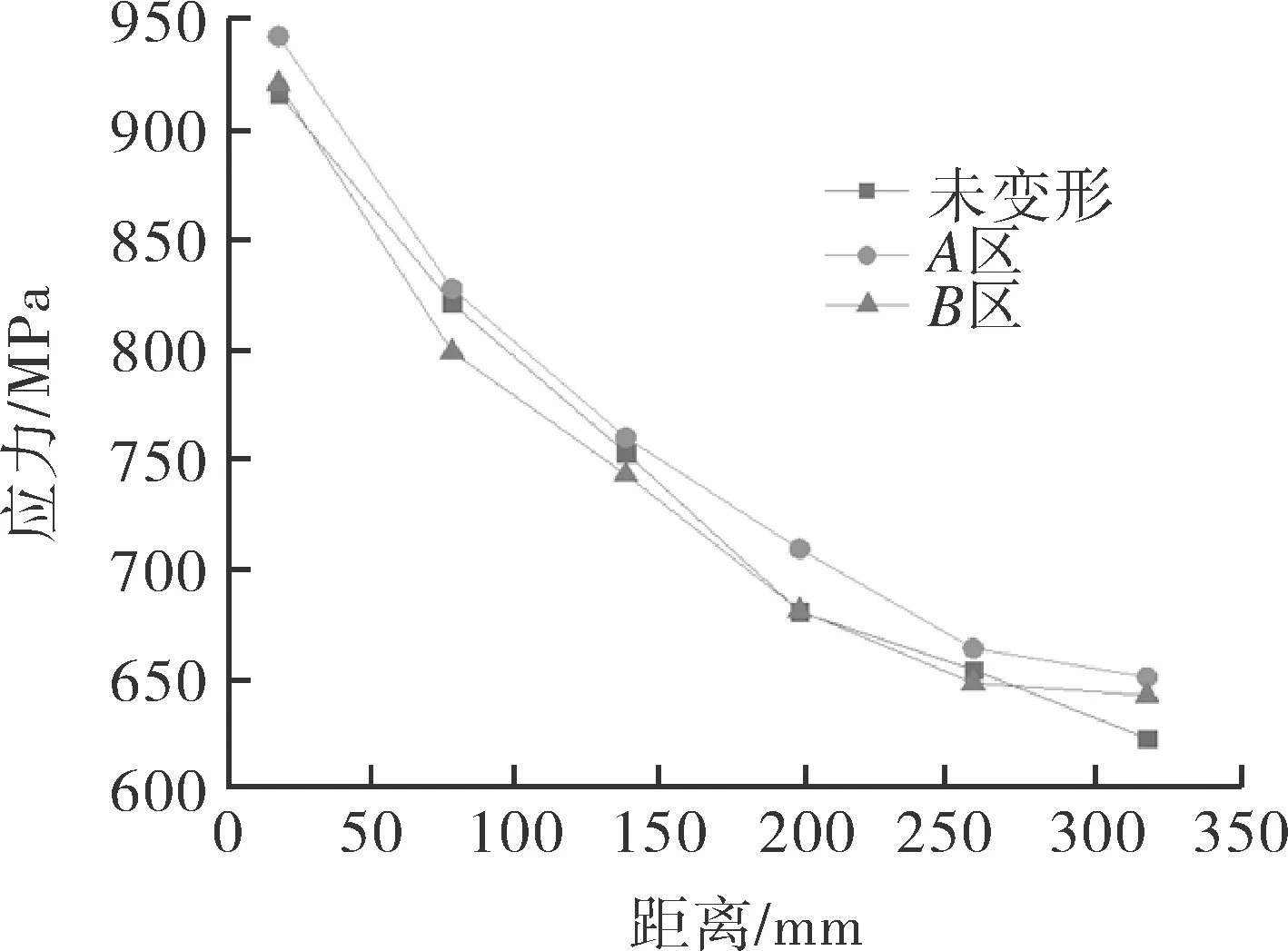
图12 最大等效应力随冷点间距的变化曲线Fig.12 The variation curve of the maximum equivalent stress with the distance between cold spots

4 结论

(1)冷点处套合最大等效应力出现在冷点上下边缘、最小等效应力出现在冷点左右边缘，A区、B区最大等效应力较未变形分别提高6.23%和6.28%。

(2)A路径冷点及其边界处的轴向应力大于周向应力，这是由于A路径焦炭分布不均匀且只能单向收缩所致。A、B路径冷点内周向应力为拉应力，冷点外区域周向应力为压应力。B路径冷点边缘轴向应力出现负值，轴向受压。

(3)对于无焦冷点模型，A区、B区的最大等效应力相较未变形模型分别提高了8.53%和14.44%；对比同一变形下冷点套合前后最大等效应力，未变形模型提高42.5%，A区提高39.5%，B区提高30.9%。

(4)冷点套合最大等效应力随着冷却水温的升高而降低，变形模型变化更明显。两冷点沿竖直方向排列时产生的等效应力最大，两点距离增加应力减小，变形模型比未变形模型应力下降更快；两点距离近时，调整距离，应力降幅明显，距离变远时，应力下降缓慢。