转子偏心凸极永磁电机电枢磁场解析研究
曹晴,李槐树,周羽,周石
(海军工程大学电气工程学院,武汉430033)
转子偏心凸极永磁电机电枢磁场解析研究
曹晴,李槐树,周羽,周石
(海军工程大学电气工程学院,武汉430033)
本文基于许-克变换针对转子偏心凸极永磁电机建立了磁场计算模型。首先计算方波磁势作用下电机的直、交轴电枢磁场;然后计算不规则磁势分布条件下的直、交轴电枢磁场;电枢磁场即为两者叠加。该方法适用于各种偏心情况下的电机磁场计算。将本模型计算的电枢磁场分布与有限元比较,结果吻合,证明其准确性和有效性。
转子偏心凸极永磁电机直、交轴电枢磁场
0 引言
凸极永磁电机具有高功率密度、高过载能力、易于弱磁调速、调速范围宽、突出的转矩控制能力等优点。因此广泛应用于风力发电、航空航天、数控加工以及新能源混合电动汽车等领域[2]。采用转子偏心结构的凸极PMSM,气隙不均匀,气隙磁场中的谐波含量减小,因而电动势和电流的谐波含量减小,附加的谐波铁损和铜损减小,使得电机效率大幅提升[3-4]。转子偏心凸极永磁电机结构复杂,利用有限元计算,电机结构参数改变时需重新建立模型,剖分网格,使用不够便捷。解析计算法可方便快捷的进行电机结构参数的更改,优化电机性能。
现有运用解析法进行磁场计算和分析的研究,主要针对表贴式永磁电机,凸极永磁电机通常采用有限元法进行磁场计算,少有文献对复杂结构的凸极永磁电机磁场计算提出一般的解析表达式。如文献[5]采用解析法计算考虑开槽的分数槽集中绕组永磁同步电机电枢反应磁场,分析了不同极槽配合电机的电枢反应磁场的谐波成分和开槽对谐波成分和幅值的影响;文献[6]采用解析法计算表贴式永磁电机空载气隙磁场,求解拉普拉斯方程和泊松方程,通过矢量磁位求得气隙磁通密度表达式;文献[7]、[8]采用有限元数值计算得到嵌入式永磁电机的气隙磁密波形,充分考虑电机的漏磁、饱和等因素的影响,计算精度高。为了简化其磁场计算,方便电机结构参数调整,优化电机,有必要对此类结构复杂永磁电机电枢反应磁场的一般分布规律进行研究。
本文首先利用许克变换得到的隐函数公式分别推导了电枢磁势为方波磁势时直轴电枢磁场和交轴电枢磁场,以此为基础求得不规则磁势分布时的直、交轴电枢磁场在气隙中的分布规律,最后通过与有限元法计算结果的对比分析,证明其有效性和准确性。
2 凸极永磁电机解析模型
为简化计算,在不影响电机性能计算的前提下,作如下基本假定:
1)定转子内表面光滑;
2)永磁体磁导率近似与空气相等;
3)铁心磁导率为无穷大;
4)忽略涡流和饱和效应。
转子偏心凸极永磁同步电机的结构示意图如图1所示。点O为定子轴心,H为转子极弧中心与电机轴心的偏心距离,Rs为定子内半径,δmin定转子间的最小气隙长度,δ(θ)定转子间不同气隙空间角对应的气隙长度,δmax定转子间最大气隙长度。

图1 偏心凸极永磁同步电机的结构示意图
3 电枢磁场解析计算
基于双反应理论,电枢磁场包括直轴电枢磁场和交轴电枢磁场,两者叠加即为电枢反应磁场。
3.1直轴电枢磁场解析计算
直轴磁路中由于永磁体的存在,当直轴磁势作用于直轴磁路时,一部分降在气隙上,一部分降在永磁体所占的区间。其走向分布见图2。直轴电枢磁场由直轴电枢磁势fd和转子铁心磁势Fm共同作用产生,转子铁心磁势Fm是与电枢磁势大小相关的方波磁势。区间I、II的磁通分别指直轴电枢磁势fd、转子铁心磁势Fm单独作用时的磁通,两者磁通的叠加即为气隙部分磁通。
根据磁通的走向,由磁通连续性定理可知:

区间I的磁通ΦdI:

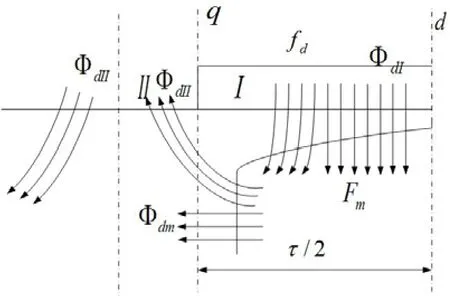
图2 直轴磁通走向分布
区间II的磁通ΦdII:

经过永磁体部分的磁通Φdm:

由(1)、(2)、(3)、(4)解得

其中:σ为漏磁系数;μ0=4π×10-7为真空磁导率;Fdm为直轴电枢磁势的最大值;Fm为铁芯内部磁势;Bd1为直轴电枢磁势产生的磁通密度;Bd2为铁心磁势产生的磁通密度;l为电机轴向长度。
作用在气隙上的磁动势为方波磁势时,在气隙中产生的直轴相对磁通密度Bd,利用许克变换得到的直轴磁密隐函数公式(6)求得。

其中:θ为气隙空间电角度;pα极弧系数;为极距,p为极对数;为得到的直轴相对磁通密度,相对磁通密度指最大磁通密度为“1”的磁通密度分布。
直轴电枢磁势为方波时,直轴电枢磁势产生的磁场和铁芯磁势产生的磁场在气隙中的分布规律一致,只是幅值大小不相同,因而有:

实际运行中,电机直、交轴电枢磁势并非为方波磁势,而是随着转子位置的不一样,呈不规则形状分布,因此电机电枢磁场的计算,须考虑不同磁势分布情况。
对于直轴电枢磁场,直轴电枢磁势为任意磁势时,直轴电枢磁势作用产生的磁场和铁芯磁势产生的磁场在气隙中的分布规律不一致,幅值大小也不相同,直轴电枢磁势作用产生的磁场在气隙中的分布规律与直轴电枢磁势分布规律相关,而铁心磁势始终为方波磁势,则其分布规律不变:

直轴电枢磁势作用产生的磁场幅值和铁芯磁势作用产生磁场的幅值分别为:
则最终得到的直轴电枢磁势为方波、任意波磁势时,直轴电枢磁场的一般表达式分别为:
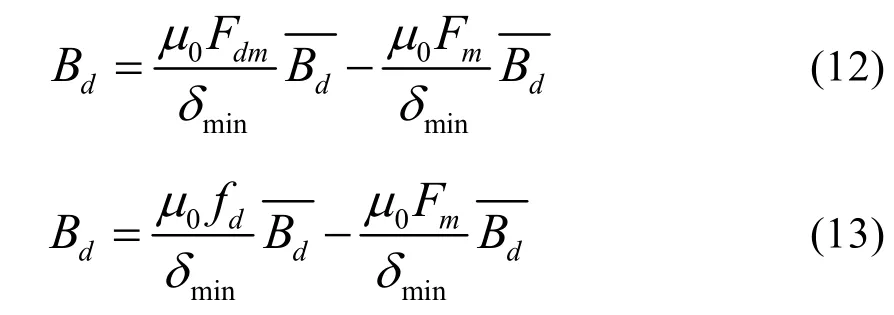
3.2交轴电枢磁场解析计算
作用在气隙上的磁动势为方波磁势时,在气隙中产生的交轴相对磁通密度,利用许克变换得到的交轴磁密隐函数公式(14)、(15)得到。

其中,u=0~1为中间变量,bs0为极间距。
交轴电枢磁势为方波磁势时产生的交轴磁场在气隙中的分布为:

交轴电枢磁势为任意磁势时,产生的交轴磁场在气隙中的分布与交轴电枢磁势在气隙中的分布有关,即:

其中,fq为交轴电枢磁势,Fqm为交轴电枢磁势的最大值。
此时,交轴电枢磁势作用产生磁场的幅值:

最终得到交轴电枢磁势为方波、任意波磁势时,交轴电枢磁场的一般表达式分别为:

4 解析法与有限元法结果对比分析
凸极永磁同步电机磁场的实验验证不方便实施,采用被大家认可的有限元的方法验证此方法的准确性。解析计算方法得到的结果与相应的有限元的方法得到的结果相吻合,则可证得解析计算方法的准确性。以4极48槽的凸极永磁电机样机为算例进行验证。偏心凸极永磁电机主要结构尺寸参见表1。

表1 偏心凸极永磁电机主要结构尺寸
直、交轴有限元计算模型如图3(a)、(c)所示。解析法与有限元法得到的电枢磁场在气隙空间的分布规律的对比如图3(b)、(d)所示。由于定子开槽的影响,有限元计算波形在施加电流位置会有较大突变,而采用解析法计算的直、交轴电枢磁场磁密波形与有限元计算出的磁密波形仅在施加电流的位置有差异,其余位置均能较好吻合。
有限元计算得出的波形在施加电流位置会有较大突变的原因在于有限元开槽的槽口边缘聚磁效应导致高次谐波幅值加大,使得开槽点磁密出现大的突变,当不考虑开槽影响时,突变也就不存在了,而本文解析计算方法不考虑开槽的影响,因而两者波形在槽口施加电流处会有一定差别。磁密的计算是为了分析计算电机电感参数和电机性能,通常开槽影响可通过卡氏系数进行修正。
5 总结
本文利用许-克变换得到的隐函数公式,采用基于方波磁势磁场的解析计算方法来进行转子偏心凸极永磁电机的磁场解析研究,以一台4极48槽的电机为样机,计算电机交直轴电枢反应磁场,并通过与有限元数值计算的对比,验证了该方法的准确性和有效性。
该方法具有如下优势:1.能够方便快捷、准确有效地进行复杂结构嵌入式永磁电机的磁场计算;2.针对电机的不同性能要求,可快速有效地进行电机结构参数的更改,利于电机的优化设计。


图3 解析法与有限元法电枢磁场对比
[1]王庆春.表面磁体永磁电机主磁场的分布特性[J].船电技术,2000,(1):17-21.
[2]吴海鹰.永磁电机电磁计算[J].船电技术,2004,(5):18-22.
[3]黄克峰,李槐树,金朝红,李帅.低速大推力圆筒永磁直线电动机磁场分析[J].微特电机,2012,40(2):4-6.
[4]黄克峰,李槐树,周羽.三相切向结构永磁电动机电感参数解析计算[J].微特电机,2010,(7):7-11.[5]林福,左曙光,马琮淦,谭钦文.考虑开槽的分数槽集中绕组永磁同步电机电枢反应磁场解析计算[J].电工技术学报,2014,29(5):29-35.
[6]章跃进,江建中,屠关镇.应用数值解析结合法计算旋转电机磁场[J].电工技术学报,2004,19(1): 7-11.
[7]陈超,刘明基,张健,陈伟华,罗应立.利用不均匀气隙优化自起动永磁电机的气隙磁密波形[J].电机控制与应用,2010,37(7):1-5.
[8]王玉彬,孙建鑫.分数槽集中绕组嵌入式永磁同步电机设计[J].电工技术学报,2014,29(5):70-75.
[9]石有计.内置式永磁同步电动机电感参数计算分析[J].微特电机,2014,42(4):4-7.
[10]ChauKT,ChanCC,LiuC.Overviewof permanentmagnet brushless drives for electric and hybrid electricVehicles[J].IEEE Transactions on Industrial Electronics,2008,55(6):2246-2257.
Analyticalstudy on Calculating Armature-reaction Field ofsalient PMSM with Eccentric Rotor
Cao Qing,Li Huaishu,Zhou Yu,Zhoushi
(College of Electrical Engineering,Naval University of Engineering,Wuhan 430033,China)
Models based onschwarz-Christoffel's transformation of asalient PMSM with rotor eccentricity is presented.At first,motor's direct-quadrature(d-q)axis's armature-reaction field undersquare wave magnetomotive force is calculated.Then,d-q armature-reaction field under magnetomotive force without regular distribution is analyzed.Finally,armature-reaction field can be obtained bysuperposing them.This method can be applied to magnet calculation of different types of motors with rotor eccentricity. Armature-reaction field of this motor was calculated by using this analytical method and Finite Element Method(FEM).The resultsshows that the two cases agree well,and theValidity and accuracy of the presented method areVerified.
eccentric rotor;salient PMSM;d-q axis;armature-reaction field
TM351
A
1003-4862(2015)10-0074-04
2015-08-25
曹晴(1990-),女,硕士研究生。研究方向:异步起动永磁同步电动机。

