带测量偏置估计的鲁棒卡尔曼滤波算法

朱光明,蒋荣欣,周 凡,田 翔,陈耀武

（1.浙江大学数字技术及仪器研究所,浙江杭州310027；2.浙江省网络多媒体技术研究重点实验室,浙江杭州310027）

带测量偏置估计的鲁棒卡尔曼滤波算法

朱光明1,2,蒋荣欣1,2,周 凡1,2,田 翔1,2,陈耀武1,2

（1.浙江大学数字技术及仪器研究所,浙江杭州310027；2.浙江省网络多媒体技术研究重点实验室,浙江杭州310027）

针对测量系统中同时存在未知的测量偏置和随机测量噪声的问题,提出带测量偏置估计的鲁棒卡尔曼滤波算法.该算法利用非零均值高斯分布对测量系统中的测量偏置和随机测量噪声进行建模,利用正态-逆威沙特分布拟合该高斯分布的均值和协方差.该算法利用变分贝叶斯方法对该高斯分布和正态-逆威沙特分布的混合模型的时变参数进行逼近推断,在利用容积卡尔曼滤波算法进行系统状态迭代估计的同时对测量偏置进行估计以及对时变随机噪声协方差进行跟踪,在进行测量偏置估计的同时增强了滤波算法对测量野值的鲁棒性.仿真实验证明了该算法在保证系统状态估计精度的同时,能够高精度估计出测量偏置并增强了滤波算法的鲁棒性.

测量偏置估计；鲁棒性；正态-逆威沙特分布；变分贝叶斯；容积卡尔曼滤波器

卡尔曼滤波算法是一种建立在隐马尔科夫模型之上的高效递归滤波算法［1］.在隐马尔科夫模型中,系统的状态不能被直接观测,但可以通过测量系统的测量结果进行推断［2］.在测量系统中主要存在2种类型的误差：随机误差和系统误差.

随机误差一般表现为服从高斯分布的加性随机测量噪声.在实际工程应用中,测量值中会存在不符合高斯分布的野值.学生t分布的重尾特性使其比高斯模型更能表征实际情况下的测量噪声分布,在鲁棒性的卡尔曼滤波器中得到应用［3］.由于学生t分布在积分运算时的局限性,往往会使用混合高斯模型来近似学生t分布,并对高斯模型的协方差引入符合伽玛（Gamma）分布的尺度因子［4］.直接利用高斯分布和其他分布联合建模测量噪声分布的方法在近年来被不断提出［5-8］.Sarkka等［5］利用高斯模型来拟合测量噪声,并利用多个逆伽玛（inverse Gamma,IG）分布来拟合高斯模型协方差矩阵对角线上的各个元素.针对多维测量噪声的情况,Agamennoni等分别利用威沙特（Wishart）分布来拟合精度矩阵［6］和利用逆威沙特（inverse Wishart,IW）分布来拟合协方差矩阵［7］,Sarkka等［8］利用逆威沙特分布来拟合协方差矩阵,分别推导出了线性系统和非线性系统中自适应的鲁棒卡尔曼滤波器.然而,测量噪声的非高斯特性使系统无法获得传统的解析解.针对该问题,变分贝叶斯方法在上述算法中得到应用.变分贝叶斯利用共乐指数域函数的性质［9］,保证了近似分布能够充分逼近原分布.

系统误差一般表现为一种确定性的测量偏置,需要对其进行估计并对测量系统进行误差补偿.基于极大似然的偏置估计法［10］和基于伪测量的偏置估计法［11］被应用到测量系统的测量偏置估计中.在统计学研究领域有很多方法来同时估计测量偏置和随机测量噪声［12］,这些方法一般应用于同一状态有很多测量值的情况.在本文要处理的问题中,同一状态在同一测量系统中只有单个测量值.Ozkan等［13］提出基于粒子滤波器和正态-逆威沙特分布的滤波算法来估计高斯测量噪声的均值和协方差,但当异常测量残差相比测量噪声协方差很大时会得到极小的粒子权重,造成采样粒子的非常严重的快速退化现象,算法的鲁棒性较差.增广状态粒子滤波算法［13］将所有未知参数都增广到系统状态向量中,利用高斯随机行走的方法对测量偏置进行估计,利用逆伽马分布对随机测量噪声协方差进行估计.但是,增广状态向量增加了状态向量的维度,导致运算量呈二次多项式级增长.

针对上述问题,为了能够同时对测量偏置和随机测量噪声进行处理,本文提出一种基于正态-逆威沙特（normal-inverse-Wishart,NIW）分布和变分贝叶斯方法的带测量偏置估计的鲁棒卡尔曼滤波算法,通过实验仿真验证了该算法的有效性.

1 模型描述

针对一般的隐马尔科夫模型,动态过程可以表征如下：

式中：xn为系统状态,zn为测量系统的测量值,f n为状态转移函数,hn为测量函数,un和vn分别为过程噪声和随机测量噪声,bn为测量偏置.

为了便于同时对测量偏置和随机测量噪声进行建模,式（2）可以转化为如下形式：

利用非零均值的高斯模型来同时表征测量偏置和随机测量噪声.在本文提出的算法中,利用en来表示测量残差,利用逆威沙特分布来拟合测量噪声wn的协方差矩阵∑n,利用正态分布来拟合测量噪声wn的均值μn,因此可以将测量系统表示如下.

式中：νn和Vn分别为逆威沙特分布的自由度和尺度矩阵,mn为参数μn的期望,κn为参数μn的协方差的尺度因子.根据式（4）中参数μn和∑n的概率分布模型,联合分布服从正态-逆威沙特分布,即p（μn,∑n）＝NIW（mn,κn,νn,Vn）.由于正态-逆威沙特分布是多维高斯分布的均值和协方差的共乐先验分布,本文算法选择正态-逆威沙特分布作为多维高斯分布的均值和协方差的概率分布模型.

2 本文算法

2.1 变分贝叶斯近似

结合式（3）、（4）,测量噪声均值μn－1和协方差∑n－1的基于测量残差e1：n－1的后验条件概率分布可以表示为

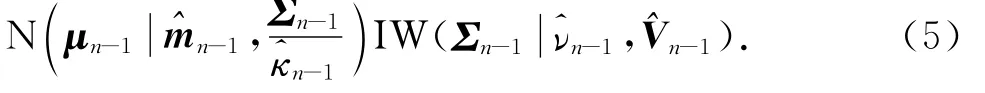
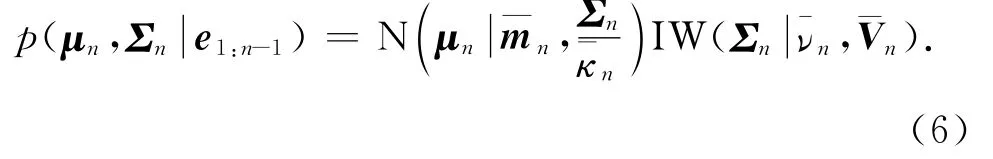
在根据贝叶斯推断原理利用式（6）和似然函数p（enμn,∑n）对后验概率分布p（μn,∑ne1：n）进行计算时,得到的后验概率分布函数是无法直接进行解析处理的.为了解决该问题,本文算法利用变分贝叶斯原理对后验概率分布进行近似,即

在变分贝叶斯近似方法中,通过近似分布和真实后验分布的KL-散度［14］的最小化来对近似分布进行求解.该近似分布和真实分布的KL-散度定义为

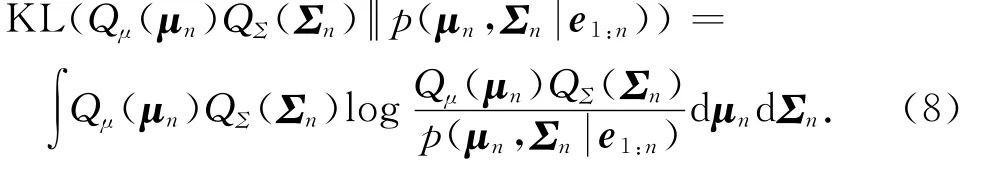
根据变分贝叶斯近似方法基于最小化KL-散度的求解过程,近似分布Qμ（μn）（或QΣ（∑n））相对于QΣ（∑n）（或Qμ（μn））的解的形式如下：

结合式（4）、（6）,式（9）中的对数式子部分可以推导得出如下形式：

式（9）中的第1个积分运算可以推导如下：

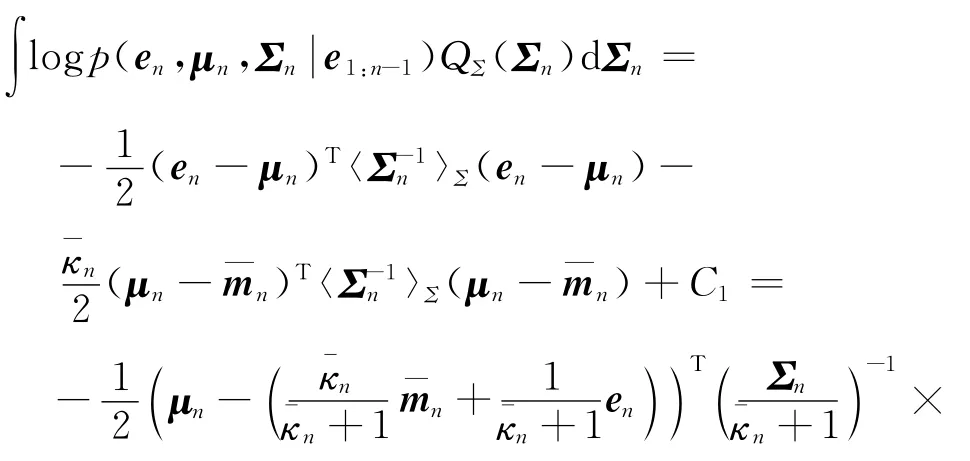
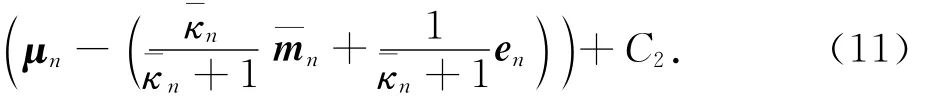
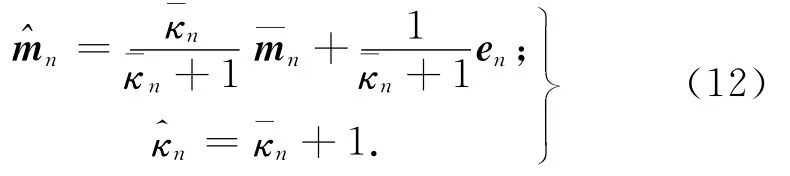
同理,式（9）中的第2个积分运算可以推导如下：

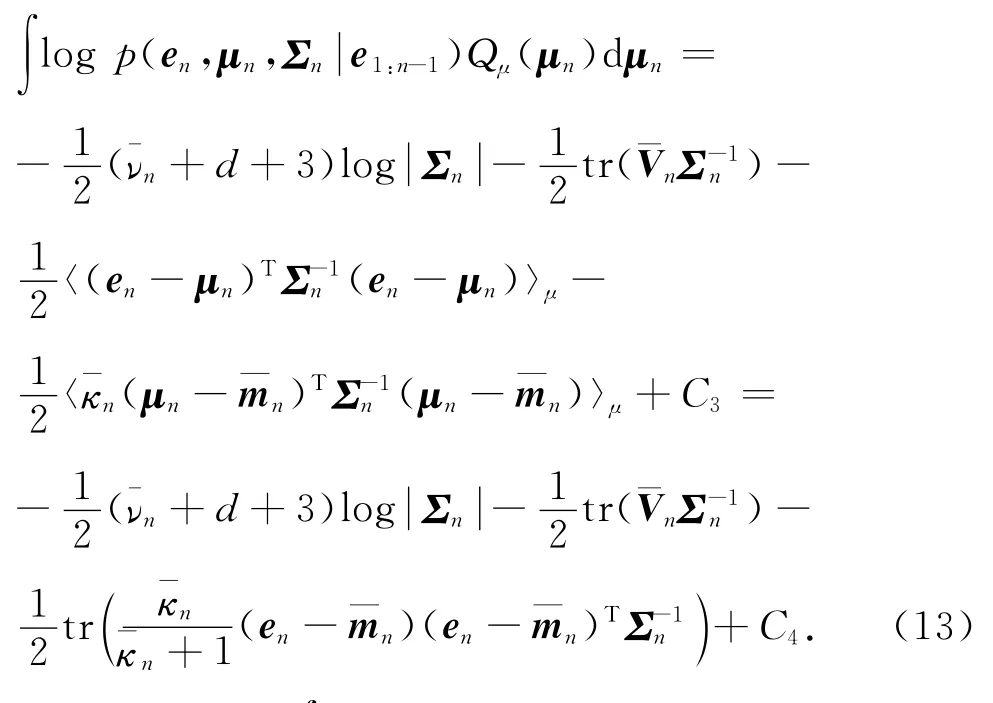
式中：〈·〉μ＝∫（）·Qμ（μn）dμn为相对于近似分布Qμ（μn）的期望值,C3和C4为和μn无关的常数.对于服从高斯分布的μn,式（13）中第一个〈·〉μ式子可以推导如下：

同理,式（13）中第二个〈·〉μ式子可以推导如下：

结合式（12）、（14）和（15）,式（13）中的积分运算可以化简到式（13）的最终形式,从而可以求出近似分布QΣ（∑n）的后验概率分布参数如下：

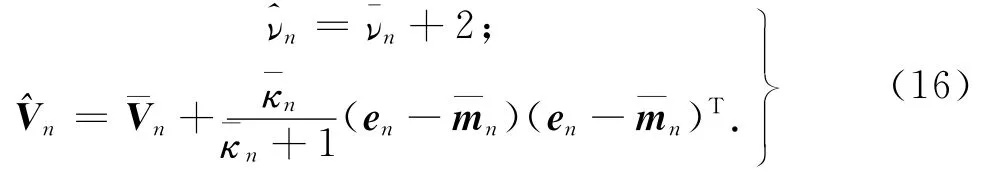
2.2 带测量偏置估计的鲁棒卡尔曼滤波算法

结合变分贝叶斯近似方法,本文提出非线性的带测量偏置估计的鲁棒卡尔曼滤波算法.容积卡尔

式中：dx为状态向量的维度,［1］i为容积点［15］.

为了能在利用卡尔曼滤波器进行系统状态估计过程中快速估计出测量噪声概率分布模型的参数以便快速获得系统状态的最佳估计,在滤波算法迭代过程中测量噪声概率分布模型参数的预测起到至关重要的作用.结合系统状态xn的预测p（xn＋1｜xn）过程,参数μn和∑n的概率分布模型的参数可以进行预测,即p（μn＋1｜μn）和p（∑n＋1｜∑n）.根据参数μn的稳定特性和∑n的时变特性,本文算法使用如下参数预测模型［13］：

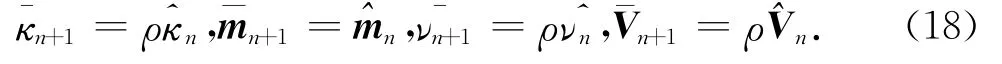
式中：ρ为预测更新系数.

综合容积卡尔曼滤波器和正态-逆威沙特分布参数迭代估计,本文提出的鲁棒滤波算法可以归纳如下.

1）系统状态和参数的初始化：

2）基于时间n（n＝0,1,…）进行迭代

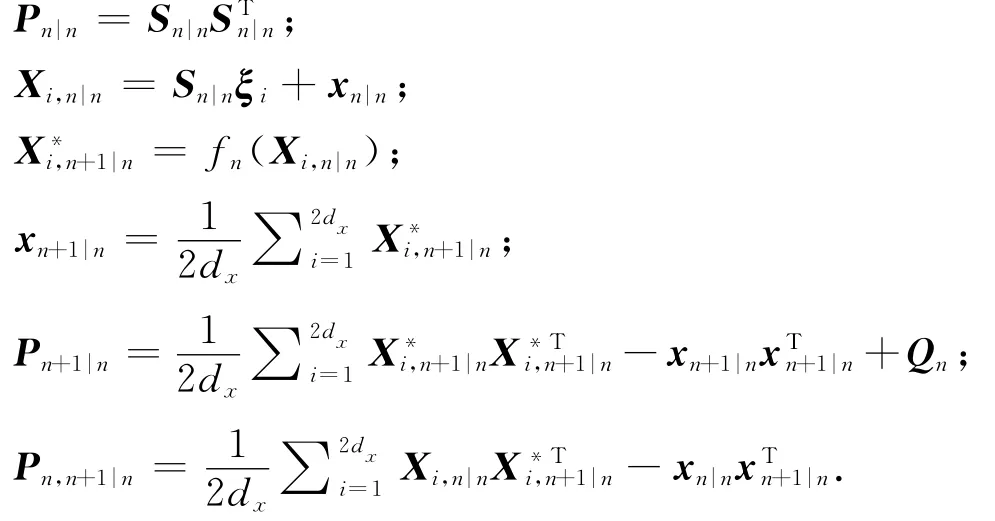
a）利用容积粒子进行系统状态预测曼滤波器（cubature Kalman filter,CKF）是一种基于容积数值积分准则的贝叶斯滤波器,核心思想是利用Spherical-Radial准则采样2dx个等权值容积点来实现非线性估计［15］.具体采样过程如下：

b）根据式（18）进行测量噪声模型参数预测

c）利用容积粒子进行测量结果预测

e）测量噪声模型参数收敛后输出估计结果：

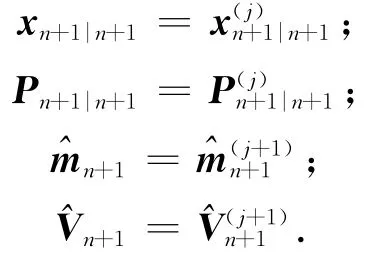
其中,φn＋1｜n表示变量φ的先验预测值,φn｜n表示变量φ的后验估计值,Sn｜n为协方差矩阵Pn｜n的平方根.容积卡尔曼滤波器的各个步骤的详细解释可参考文献［15］,本文不再赘述.＝0表示事先未知各个测量系统测量偏置的先验信息＝dz＋2和＝∑0的选取使得对随机测量噪声协方差的估计值等于各个测量系统的随机测量噪声协方差的先验值∑0.

本文提出的算法与标准容积卡尔曼滤波算法的重要区别如下：本文算法利用正态-逆威沙特分布来拟合测量噪声的均值和协方差,并利用测量噪声均值和协方差的实时估计值取代标准容积卡尔曼滤波算法中的固定值；系统状态的后验估计要迭代多次直至测量噪声模型参数收敛；测量偏置的估计与补偿以及测量噪声协方差的实时估计增强了算法的鲁棒性.

3 实验结果与分析

3.1 仿真模型建立

为了验证本文算法的有效性,对经典的纯距离多传感器目标跟踪问题进行建模仿真.目标的运动模型采用二维固定转率模型,即

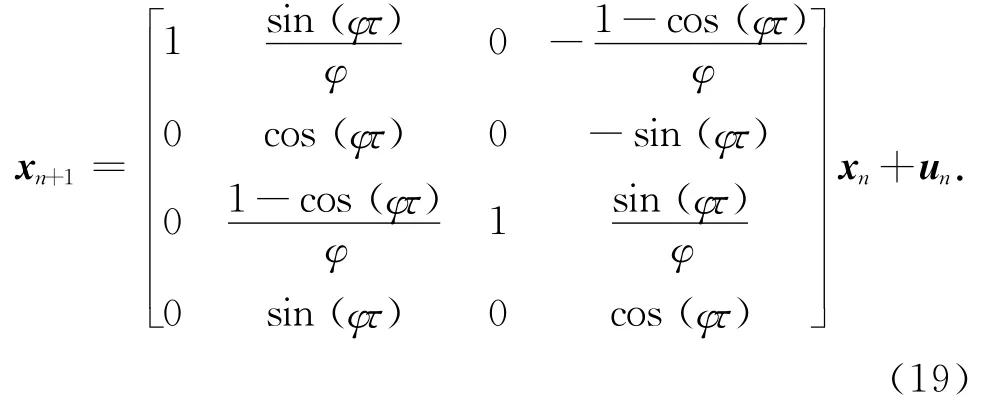
式中：rn＝［x1,n,x2,n］T为运动目标位置的估计值, lj为传感器j的位置,υ为信号传播速率,wn为式（3）中描述的测量噪声,· 为欧式距离.

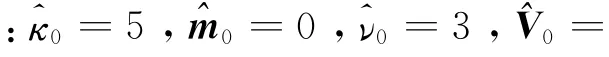
在相同的仿真环境下,通过对比以下4种方法的仿真结果来验证本文算法的优势.

·CKF-NIW：本文提出的基于正态-逆威沙特分布和容积卡尔曼滤波器的鲁棒滤波算法.

·CKF-NIG：基于文献［16］的正态-逆伽玛（normal-inverse-Gamma,NIG）模型和容积卡尔曼滤波器的鲁棒滤波算法.

·CKF-IW：基于CKF-NIW估计出的测量偏置期望值,只利用逆威沙特分布估计测量噪声协方差的鲁棒滤波算法.

·CKF-True：测量噪声概率分布模型参数已知情况下的标准容积卡尔曼滤波算法.

鉴于利用逆威沙特分布拟合测量噪声协方差的算法的鲁棒性在文献［7,8］中已得到验证,本文的实验部分重点验证状态估计和测量偏置估计的性能.

3.2 结果分析

分析各种算法的目标跟踪结果.图1、2分别展示了运动目标状态估计的位置分量和速度分量的均方根误差（RMSE）结果.图中,SRMSE、vRMSE分别为位置分量和速度分量的均方根误差.对比算法CKFNIW、CKF-IW和CKF-True的仿真结果可知,当只有测量噪声协方差未知时,利用逆威沙特模型拟合协方差的分布可以获得较好的状态估计.当测量偏置和测量噪声协方差都未知时,系统误差和随机误差的同时存在造成测量偏置和随机测量噪声的相互耦合,因此在数值上很难精确分离出测量偏置和随机测量噪声.测量偏置的估计精度直接影响了测量残差的计算,进而直接影响了状态估计的精度.随机测量噪声协方差的估计精度直接影响了预测测量协方差矩阵的计算,从而影响卡尔曼增益的计算,最终影响状态估计的精度.当测量偏置和随机测量噪声协方差都未知时,算法CKF-NIG和CKF-NIW获得相对较差的跟踪结果.

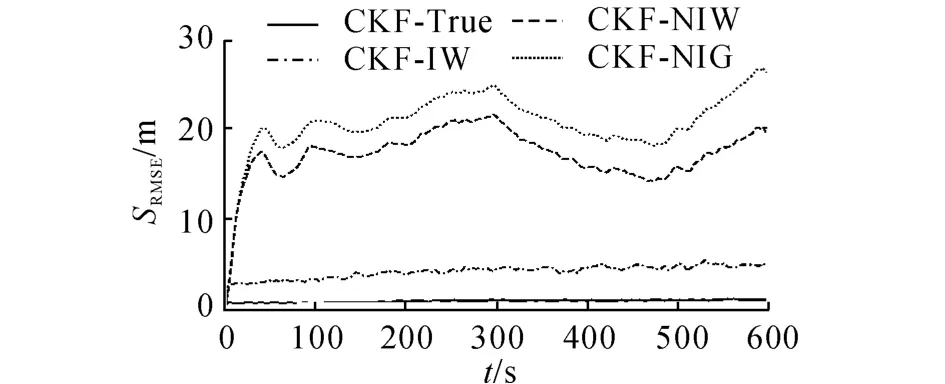
图1 位置估计均方根误差对比(ρ＝1—exp(—4))Fig.1 RMSE comparison of position estimation（ρ＝1－exp（－4））

图2 速度估计均方根误差对比(ρ＝1—exp(—4))Fig.2 RMSE comparison of velocity estimation（ρ＝1－exp（－4））

对比算法CKF-NIG和CKF-NIW的仿真结果可知,无论是在位置分量的估计上,还是在速度分量的估计上,本文提出的CKF-NIW算法都要获得较好的结果.这是因为正态-逆伽玛模型只注重协方差矩阵对角线上元素的估计,而正态-逆威沙特模型对整个协方差矩阵进行估计.无论是本文的仿真结果,还是文献［8］的仿真结果,逆威沙特分布都表现出了相较于逆伽玛分布的优越性.

对比图1、2的结果可知,测量偏置对速度分量的影响小于对位置分量的影响.这是因为本实验的测量系统只对目标的位置信息进行观测,因此测量偏置和随机测量噪声对位置分量的估计产生直接的影响.利用相邻时间位置分量的差值进行速度分量的估计抑制了测量偏置对速度分量估计的影响.

分析测量偏置的估计结果.图3展示了算法CKF-NIG和CKF-NIW对测量偏置估计的结果.尽管4个传感器节点拥有不同的测量偏置,但是本文提出的算法仍然可以快速估计出各个传感器节点的测量偏置,并在整个过程中保持相对稳定的估计值.算法CKF-NIG和CKF-NIW的测量偏置估计值的过程均值分别为：0.1023、0.1538、0.2020、0.2513和0.1009、0.1529、0.2015、0.2504.算法CKF-NIG和本文提出的CKF-NIW算法都采用正态分布对测量偏置的概率分布进行拟合.尽管2种算法都得到了高精度的测量偏置估计结果,但本文算法得到了相对更高的估计精度.

图3 测量偏置估计结果(ρ＝1—exp(—4))Fig.3 Estimates of measurement biases（ρ＝1－exp（－4））

分析参数更新系数ρ的取值.在本文描述的问题中同一时刻的状态在同一测量系统中只有一个测量值,因此无法利用统计方法中的多测量值的统计特性.本文算法通过参数更新系数ρ对测量偏置和随机测量噪声参数进行自适应迭代更新.根据式（12）、（16）和（18）,ρ的取值决定了单次测量值对模型参数的更新程度.图4展示了当ρ＝1－exp（－5）时的测量偏置估计结果,对比图3展示的结果可以得出：当ρ增大时,测量偏置估计对单个测量值的鲁棒性增加,进而得到更加平滑的测量偏置估计,但测量偏置估计的收敛速度略有降低.系统仿真在更新系数ρ＝1－exp（－5）时取得了更加准确的测量偏置估计,进而在对目标的跟踪上取得了更高的跟踪精度.当ρ＝1－exp（－4）和ρ＝1－exp（－5）时系统仿真取得的目标位置估计平均最小均方误差分别为：17.07和14.17.这进一步说明了测量偏置估计精度对最终目标状态的估计精度有直接影响.在实际应用中,ρ的取值要兼顾算法的整体估计精度和收敛速度.

图4 测量偏置估计结果(ρ＝1—exp(—5))Fig.4 Estimates of measurement biases（ρ＝1－exp（－5））

由于测量偏置和随机测量噪声的相互耦合,当出现幅值较大的测量噪声时,会对测量偏置的估计造成影响.鉴于测量偏置与测量系统本身的特性相关,一般可以认为测量偏置在短期内是相对稳定的.因此,充分利用测量偏置的稳定性,通过滑动窗口获取一段时期内的测量偏置估计均值,从而求出测量偏置的高精度期望值.已知测量偏置期望值,则可以利用CKF-IW算法取代CKF-NIW算法,通过适当调度2种算法以取得更好的目标状态估计结果.

为了进一步综合分析本文算法对测量偏置和随机噪声协方差进行同时估计的效果,以下仿真实验参照文献［13］,采用高斯随机噪声取代原来的服从学生t分布的随机噪声,以便直接评估本文算法对随机噪声协方差的估计精度.测量偏置分别设置为［0.01,0.05,0.1,0.15］,测量偏置估计的初值分别设置为［0.05,0.01,0.15,0.1］,高斯随机噪声协方差的标准差σw＝0.001.图5、6展示了测量偏置估计结果和测量噪声协方差标准差的估计结果.图5显示,当测量偏置估计初值为小于实际值的非零值时,测量偏置估计收敛速度略有增加；当测量偏置估计初值大于实际值时,收敛速度相比前一情况略有降低；收敛之后的估计结果与图4的结果相比并未有明显差异.这一结果证明了先验信息只对算法的收敛速度稍有影响,而对收敛后的估计结果影响甚微.

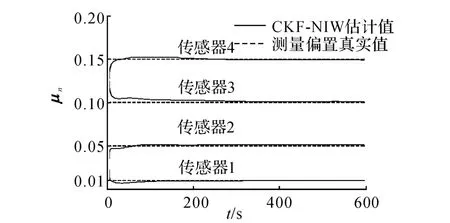
图5 不同估计初值时的测量偏置估计结果Fig.5 Estimates of measurement biases with different estimation initial values

图6结果显示,本文算法对随机噪声协方差有较好的估计结果.尽管本文算法的收敛速度不够迅速,但算法收敛之后取得了较高的估计精度,而收敛速度不足与每一时刻每个传感器只有一个测量值有关.由于测量偏置比随机测量噪声具有更强的确定性,测量偏置估计的收敛速度大于随机噪声协方差估计的收敛速度.由于本文算法的重点在测量偏置估计和对非高斯噪声的鲁棒性,对高斯随机噪声的情况不作详细讨论.

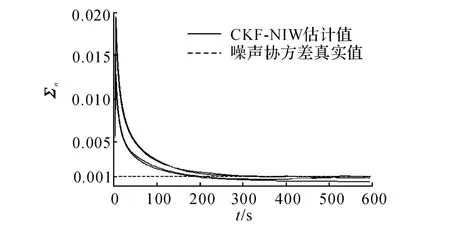
图6 测量噪声协方差估计结果Fig.6 Estimates of measurement noise covariance

4 结 语

针对测量系统中测量偏置和随机测量噪声同时存在的问题,本文提出带测量偏置估计的鲁棒容积卡尔曼滤波算法.通过将测量偏置和随机测量噪声分别建模成高斯模型的均值和协方差,本文算法利用正态-逆威沙特分布对高斯模型的均值和协方差参数的概率分布模型进行拟合.基于变分贝叶斯近似算法和容积卡尔曼滤波器,本文推导出非线性的带测量偏置估计的鲁棒卡尔曼滤波算法.通过建模仿真,本文提出的算法具有优良的系统状态估计性能,对测量偏置具有更高的估计精度,对随机测量噪声具有更好的鲁棒性.

［1］WELCH G,BISHOP G.An introduction to Kalman filtering［R］.Chapel Hill,NC：University of North Carolina,2006.

［2］RABINER L,JUANG B.An introduction to hidden Markov models［J］.IEEE ASSP Magazine,1986, 3（1）：4- 16.

［3］ZHU H,LEUNG H,HE Z.A variational Bayesian approach to robust sensor fusion based on Student-t distribution［J］.Information Sciences,2013,221（0）：201- 214.

［4］JO-ANNE T,THEODOROU E,SCHAAL S.A Kalman filter for robust outlier detection［C］//IEEE／RSJ International Conference on Intelligent Robots and Systems.San Diego：IEEE,2007：1514- 1519.

［5］SARKKA S,NUMMENMAA A.Recursive noise adaptive Kalman filtering by variational Bayesian approximations［J］.IEEE Transactions on Automatic Control, 2009,54（3）：596- 600.

［6］AGAMENNONI G,NIETO J I,NEBOT E M.An outlier-robust Kalman filter［C］//IEEE International Conference on Robotics and Automation.Shanghai：IEEE, 2011：1551- 1558.

［7］AGAMENNONI G,NIETO J I,NEBOT E M.Approximate inference in state-space models with heavy-tailed noise［J］.IEEE Transactions on Signal Processing,2012,60（10）：5024- 5037.

［8］SARKKA S,HARTIKAINEN J.Non-linear noise adaptive Kalman filtering via variational Bayes［C］//IEEE International Workshop on Machine Learning for Signal Processing.Southampton：IEEE,2013：1- 6.

［9］BEAL M J.Variational algorithms for approximate Bayesian inference［D］.London：University of London,2003.

［10］OKELLO N,RISTIC B.Maximum likelihood registration for multiple dissimilar sensors［J］.IEEE Transactions on Aerospace and Electronic Systems,2003, 39（3）：1074- 1083.

［11］TAGHAVI E,THARMARASA R,KIRUBARAJAN T,et al.Bias estimation for practical distributed multiradar-multitarget tracking systems［C］//16th International Conference on Information Fusion.Istanbul：ISIF,2013：1304- 1311.

［12］GELMAN A,CARLIN J B,STERN H S,et al.Bayesian data analysis［M］.Florida：CRC,2013.

［13］OZKAN E,SMIDL V,SAHA S,et al.Marginalized adaptive particle filtering for nonlinear models with unknown time-varying noise parameters［J］.Automatica,2013,49（6）：1566- 1575.

［14］HERSHEY J R,OLSEN P A.Approximating the Kullback Leibler divergence between Gaussian mixture models［C］//IEEE International Conference on Acoustics,Speech and Signal Processing.Hawaii：IEEE, 2007：317- 320.

［15］ARASARATNAM I,HAYKIN S.Cubature Kalman filters［J］.IEEE Transactions on Automatic Control, 2009,54（6）：1254- 1269.

［16］COWLES M K.Applied Bayesian statistics［M］.New York：Springer,2013.

Robust Kalman filtering algorithm with estimation of measurement biases

ZHU Guang-ming1,2,JIANG Rong-xin1,2,ZHOU Fan1,2,TIAN Xiang1,2,CHEN Yao-wu1,2
（1.Institute of Advanced Digital Technology and Instrumentation,Zhejiang University,Hangzhou 310027,China；2.Zhejiang Provincial Key Laboratory for Network Multimedia Technologies,Hangzhou 310027,China）

A robust Kalman filtering algorithm with estimation of measurement biases was proposed in order to handle the problem that unknown measurement biases and random measurement noises exist in the measurement system.The nonzero-mean Gaussian distribution model was utilized to model the measurement biases and the random measurement noises of the measurement system.The Normal-Inverse-Wishart distribution was utilized to estimate the mean and covariance parameters of the Gaussian distribution.The time-variant parameters of the mixed model between the Gaussian distribution and the Normal-Inverse-Wishart distribution were inferred by the variational Bayesian approximation.The measurement biases and the time-variant covariances of the random measurement noises were estimated as the system states were recursively inferred by the cubature Kalman filter.The proposed algorithm's robustness to the measurement outliers was enhanced with the estimation of the measurement biases.The simulation results demonstrate that the proposed algorithm can also precisely estimate the measurement biases and enhance its robustness with the guarantee of the high state estimation precision.

estimation of measurement biases；robustness；Normal-Inverse-Wishart distribution；variational Bayesian；cubature Kalman filter

蒋荣欣,男,副研究员.E-mail：rongxinj＠zju.edu.cn

TB 56

A

1008- 973X（2015）07- 1343- 07

10.3785／j.issn.1008-973X.2015.07.020

2014- 05- 16. 浙江大学学报(工学版)网址：www.journals.zju.edu.cn／eng

中央高校基本科研业务费专项资金资助项目；浙江省重点科技创新团队资助项目（2011R09021-06）；浙江大学基本科研业务费专项资金资助项目（2014FZA5020）.

朱光明（1987－）,男,博士生,从事无线传感器网络及信息融合的研究.ORCID：0000-0003-3214-4095.E-mail：zhgm＠zju.edu.cn