高中数学不等式易错题型及其解法探讨

丁晓璇

[摘 要]求解不等式解集是高中数学教学内容的重要组成部分，其难度较大，学生不易理解，因而常常出现错误。本文分析了高中数学不等式问题中学生容易出错的题型，如不等式与线性规划的结合、不等式中一元高次不等式问题，并分析相应的解题方法，以便帮助学生避免错误，使学生的成绩得到提高。

[关键词]不等式问题；易错题型；解题技巧

不等式是高中数学教学中的难点，历年高考试题中，无论是填空题或是计算题，都对不等式知识有所涉及。不等式知识复杂，且在数学中的应用范围较广，导致学生经常出现失误。

一、高中数学不等式问题中学生易错题型及其解题技巧

（一）不等式与线性规划相结合的问题

数学考试题目中，这类题型频繁在数学考试中出现。因其考察的范围广，对学生综合运用数学知识的能力要求较高。

题目一：由y-x+2，ykx+1，x0三个不等式组合为等式组，三项不等式所围成的平面区域面积为1 ，求解k值为多少？

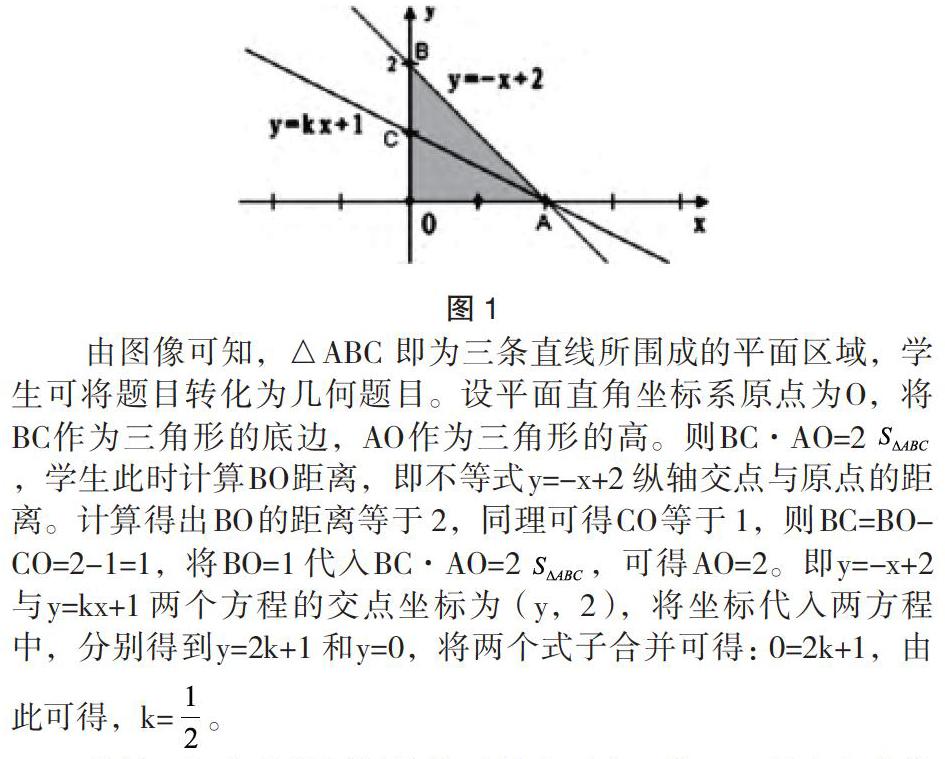
分析：学生在计算三条直线所围成的三角形区域时容易出错，该题要求学生明确三个不等式的取值范围，并画出图示。学生在解答该题时，应先绘制三条直线，并标示其共同包含的区域（如图1所示）：

由图像可知，△ABC 即为三条直线所围成的平面区域，学生可将题目转化为几何题目。设平面直角坐标系原点为O，将BC作为三角形的底边，AO作为三角形的高。则BC·AO=2，学生此时计算BO距离，即不等式y=-x+2纵轴交点与原点的距离。计算得出BO的距离等于2，同理可得CO等于1，则BC=BO-CO=2-1=1，将BO=1代入BC·AO=2，可得AO=2。即y=-x+2与y=kx+1两个方程的交点坐标为（y，2），将坐标代入两方程中，分别得到y=2k+1和y=0，将两个式子合并可得：0=2k+1，由此可得，k=。

总结：解答此类题目的技巧共有两个：其一，学生在求该类型问题或遇到求解极值的问题时，应先绘制出不等式组的可行域，将其转化为几何知识，理解可行域的几何意义，之后将不等式转化为等式，通过计算解决题目问题。其二，学生将不等式化为函数，并为函数设定一部分参考值，从函数入手，观察不同参考值下，函数图形的变化，从而逐渐锁定影响函数变化的量，对其进行求解。这两种方法是解答该类问题的主要方法。

（二）高次不等式问题

这类题型同样是高中考试中常见的问题，学生在该类题型中出现错误，原因主要有三点。第一，学生忽略了题目中部分隐性的要求，如高次分式不等式中，学生会遗忘分母不能为零这一要求。第二，学生对解集的区域不明，部分学生虽然能够得出解集的范围，但对范围边界不明，主要体现于学生不能确定解集是否要取边界值。第三，学在使用“穿根法”时，不能确定函数的升降规律。以上便是构成学生在解答问题时出错的原因。

题目二：求不等式（x+3）（x-2）（x-4） 0的解集。

分析：该题已明确给出学生函数的根，分别为：x=-3、x=2、x=4。学生能够准确在序轴中标示三个零点，将序轴分为四个区间。学生运用穿根法，从最右端的零点开始，由右上方过右端零点向左下方穿过，之后依次穿过每个零点，形成一条函数曲线图（如图2所示）。

之后学生按照题目要求，进行图像选择。因为题目要求整式小于0，所以学生应选择序轴以下的图像，即得出不等式的解集（-，-3）U（2，4）。学生继续分析题目，可以发现，题目中的不等符号是“”，因此边界值可以纳入集合当中，所以该题最终的解集为（-，-3]U[2，4]。

题目三：求解分式不等式

分析：該题解题思路与上一题基本相同。学生在计算前需将不等式形式转化为（x-2）（x+1）（x-6）（x+2） 0，学生由题得出函数（x-2）（x+1）（x-6）（x+2）=0的根，分别为：x=2、x=-1、x=6、x=-2。将四个零点标示在序轴中，并运用穿根法进行穿根，便可得到图像不等式的函数图像（如图3所示）。学生根据图像可得结果（-，-2]U[-1，-2]U[6，+）。

部分学生的解题至这一步便结束了。然而学生忘记该题是分式不等式，作为分式便具有一个限制条件：分式中分母不得为零。虽然该题没有标注，且题中所用符号为“”，但是学生依旧需要将分母为零的情况纳入考虑范围。因此，该题还需继续解答。令（x+2）（x-2）0，故而，该题最终的解集为（-，-2）U[-1，-2）U[6，+）。

总结：学生在解决该类问题时，应熟练掌握穿根法这一解题方式，运用穿根法能够提高学生的解题速度，降低题目难度。同时学生解得解集后，也应对解集的临界点进行判定，确定其是否可以纳入解集范围内，从而使解集不会出现问题。

二、结语

高中数学不等式知识与其他知识联系紧密，因此考试试题复杂多变。教师在授课时，应常常分析学生的易错点，根据易错点找寻学生出现错误的原因，帮助学生改正，从而提高学生的成绩。

参考文献：

[1]吴华妹.高中数学不等式高考试题分析与教学策略研究[J].中国校外教育，2014，S3：405.

[2]全裕刚.探究不等式在高中数学解题中的应用[J].亚太教育，2015，21：38-39.