信号与系统中“连续系统复频域分析”的教学探讨

陈光红

【摘要】介绍了《信号与系统》课程中连续系统复频域分析的原理，通过两道例题将复频域分析中相关的知识点，如求解零输入响应、零状态响应、全响应、系统函数、冲激响应、阶跃响应、判断系统的稳定性、画系统的零极点分布图、部分分式展开法求逆拉普拉斯變换等串联起来，鼓励学生将连续系统的复频域分析方法与频域分析方法、离散系统的Z域分析方法进行对比，加深知识点的理解和综合应用。

【关键词】复频域分析 零输入响应 零状态响应 稳定性 系统函数

【中图分类号】G642 【文献标识码】A 【文章编号】2095-3089（2015）10-0206-01

《信号与系统》是电子信息技术、通信技术等专业的核心课程，该课程主要讲解连续系统的时域分析、频域分析、复频域分析，离散系统的时域分析、Z域分析等，主要借助傅里叶变换、拉普拉斯变换、Z变换来分析求解系统。其中借助连续系统的复频域分析可以求解系统的响应、分析系统的时域特性、频率响应、判断系统的稳定性等[1]，连续系统的复频域分析与离散系统的Z域分析也有相似性，学好复频域分析对学习频域分析、Z域分析有很大的帮助。

通过一道例题将复频域分析中所涉及到的知识点串联起来，在教学中鼓励学生举一反三，将所学知识联系起来，综合应用。

1.连续系统复频域分析原理

连续系统复频域分析主要利用拉普拉斯变换将时域里的微分方程转化成复频域的代数方程，求出各响应的象函数，然后利用部分分式法求逆拉普拉斯变换，得出系统的零输入响应、零状态响应、全响应等。

2.连续系统复频域分析的例题

（2）判断系统的稳定性

从时域判断，Qt→∞时，h（t）→0，∴系统是稳定的；

从复频域判断，Q系统函数H（s）的极点为s=-2，符合“若全部极点都落在s平面的左半平面，则该系统必是稳定系统”[1]∴系统是稳定的。

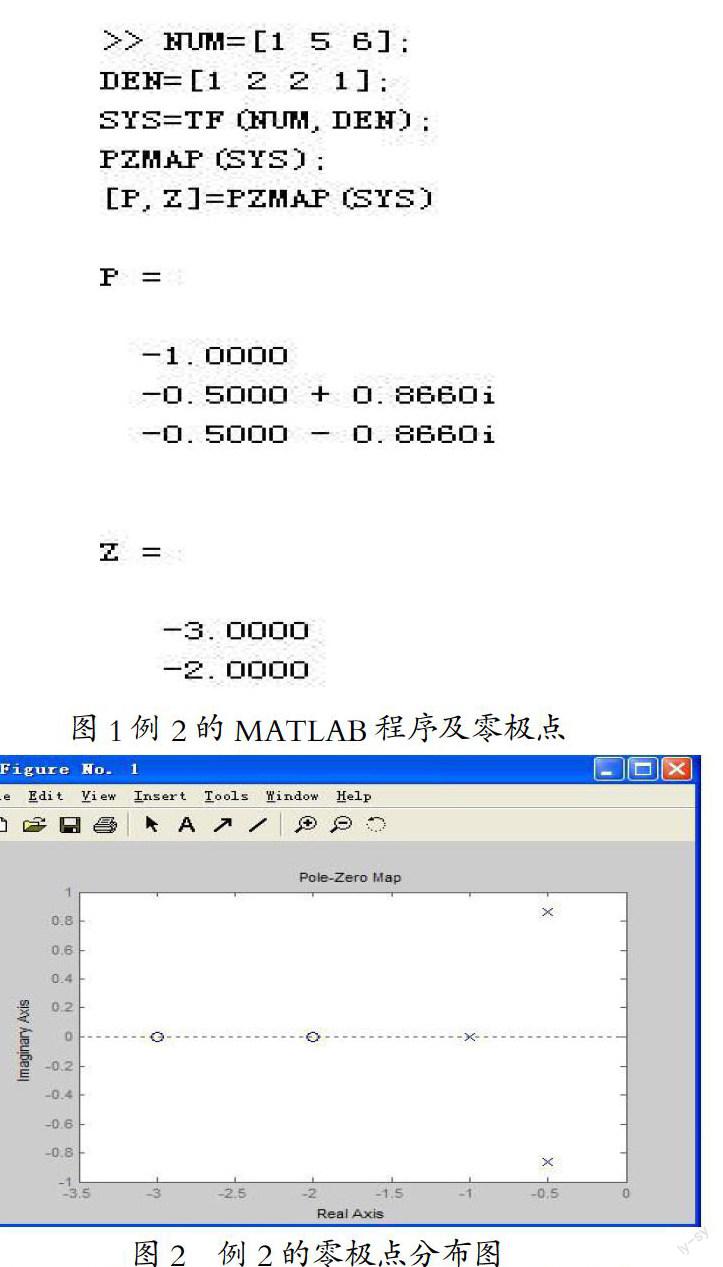
说明：对于较复杂的系统函数，若不易求出其极点（分母多项式的根），可以借助MATLAB软件简单的编程（将系统函数的分子、分母多项式的系数输入），可以输出零极点分布图，然后从图上的极点位置判断系统的稳定性。

3.结语

《信号与系统》课程理论性较强，学生学习时感觉知识点多、比较难，通过一道连续时间系统的复频域分析的例题，将复频域分析中的知识点串联起来，使学生在学习时注意知识点之间的联系，复习时可以检验自己是否已将相关的知识点掌握。

参考文献：

[1]周昌雄.信号与系统[M]. 西安：西安电子科技大学出版社，2008.5.

[2]刘国良. 信号、系统分析与控制（MATLAB版）[M]. 西安：西安电子科技大学出版社，2013.11.