交叉口左转交通流两种组织方式的延误计算模型*

林培群 顾玉牧 卓福庆 冉斌 徐建闽

(1. 华南理工大学 土木与交通学院，广东 广州510640;2. Civil and Environmental Engineering，University of Wisconsin-Madison，Madison 53076，USA)

城市交通系统中，交叉口是路网的连接点也是道路通行能力的瓶颈和交通事故的多发点，制约整条道路乃至路网的服务水平［1］. 在交叉口车流中，左转车流是产生冲突点最多的车流.在此影响下，路口通行效率大大降低，延误时间和安全隐患增加.因此，解决好交叉口的左转交通流，是提高城市路网通行能力和交通安全水平的关键.

间接左转是交叉口左转的一种独特渠化方式.该方法已经在美国的弗罗里达、新泽西、路易斯安那以及一些欧洲国家得到了成功的应用［1］. 其基本思想就是直接左转的车辆先直行，再利用交叉口下游较宽的中央分隔带掉头回转，从而提高车辆的运行高效性以及安全性.研究表明，间接左转不仅改变了车辆的运行轨迹，同时，还能够有效地分担负载在通行能力相对较大的交叉口的一部分交通负荷，在路口与路段运营效率之间找到一个平衡点［2-3］. 间接左转的方法有几种形式:街巷绕行式、右转回绕式、直行回绕式等.但是，这些方法只有在特定的交通环境下才有效，交叉口布局(中央分隔带宽度、转弯半径、道路宽度等)、交叉口的配时方案等外部条件适宜时才适合间接左转.倘若设置不当，会增加交叉口的整体延误，且会对下游交通流产生影响［4］.

在间接左转效用方面，文献［5］中在佛罗里达交通运输部赞助的一项研究中发现，使用间接左转的车辆平均等待延误小于直接左转. 文献［6］在美国佛罗里达州选择了258个信号交叉口，对其中4000起事故进行分析，发现使用间接左转可以使事故总数减少26%，即可有效提高交通运行安全.

在间接左转选址方法方面，文献［7］中对美国佛罗里达州的208个选址进行观测.通过对采集到的车辆事故数据和行程时间数据的回归分析发现，影响事故数的主要是间接左转的交通控制方式以及开口位置.文献［8］中对国内多个应用实例进行调查，并应用交通仿真的方法对间接左转组织方式的实施地点、开口间距、路段中央隔离带宽度、开口长度等影响因素作定量的分析研究，对这些影响因素的设置给出理论依据. 文献［9］中研究并得出一个定量的公式:利用上下游相邻两个交叉口信号灯的相对相位差和车辆平均车速等参数，可以得出中央分隔带缺口处距离下游交叉口的合理长度. 文献［10］中在遵循文献［9］规范的基础上，对临近路口配时进行优化，既保证了行车安全性，又能显著提高交通运行效率.

在基于仿真软件分析直接左转与间接左转优劣方面.文献［11］中研究掉头车道的选址方式以及U形转弯设置方法. 同时，通过VISSIM 仿真软件进行数据分析，比较直接左转和间接左转的延误情况.文献［12-13］中利用交通仿真软件VISSIM 对可调头的城市交叉路口进行交通流微观仿真，采用延误分析法，得到调头交叉口车流延误数据，建立基于交通仿真的可调头交叉口延误－流量关系曲线，据此对交叉口调头位置的设置给出一个优选方案. 文献［14］中结合两种交通分析工具 FRESIM 和NETSIM，以延误和行驶时间作为评估直接左转和右转－前行－掉头性能的效率度量.

现有的文献大都是通过仿真来研究直接左转和禁左掉头两种方案的延误情况.而且，一般是研究某一车道或者是某一方向的延误情况，没有进行交叉口整体平均延误的精确建模与分析.同时，没有充分考虑在选择间接左转组织方式后，重新调整交叉口配时方案，从而更好地发挥道路通行能力. 有鉴于此，文中主要是通过数学建模，合理配时，定量分析，以获得两种方案下整个交叉口的平均延误.从而，提供一种定量可行的比较思路.

1 左转交通流常用交通组织方式

1.1 左转三相位组织方式

图1 为常见的左转三相位交通组织方式.

当交叉口主次路相交，且主路左转流量较大、次路左转流量较小时，可采取三相位的方式，即主路设置左转专用车道和相位，次路各向同时放行.

图1 直接左转三相位组织方式Fig.1 Direct left-turn for three-phase organization

1.2 右转－前行－掉头两相位组织方式

图2 为常见的禁左掉头两相位交通组织方式.相位设计中，将原本左行的车辆通过右转－前行－掉头(R-S-U)的方式实现左转，从而减少其他方向车流等待左转专用相位而造成的延误. 采用这种方式，在一定的情况下，优于设置左转专用相位的组织方式.

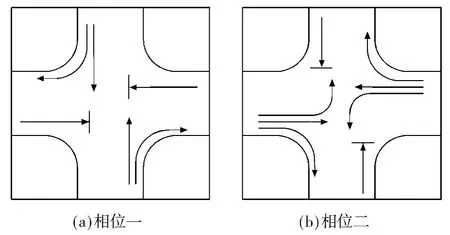
图2 右转－前行－掉头两相位组织方式Fig.2 R-S-U for two-phase organization

2 两种交通组织方式下交叉口整体延误的计算模型

为了减少车辆的行车延误，交通信号设计人员会考虑禁左掉头的方式以减少其他相位车流等待左转专用相位造成的延误.但是，由于原本左行车辆通过掉头方式实现左转，也会对交通流产生额外的延误，如:左转车辆在中央分隔带的等待时间、掉头的时间、对对向车流的影响等. 所以，只有通过比较整个交叉口所有车辆的平均延误，才能更为科学合理地比较两种不同方式的优劣.

2.1 左转三相位组织方式的延误计算模型

对于常见的左转三相位组织方式，可以考虑用韦伯斯特延误公式定量计算交叉口的平均延误. 各个方向的总延误twebster计算公式为

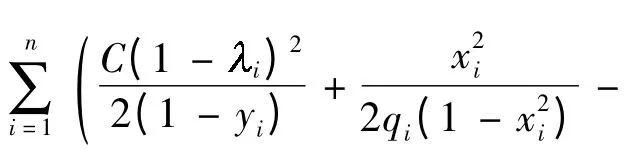
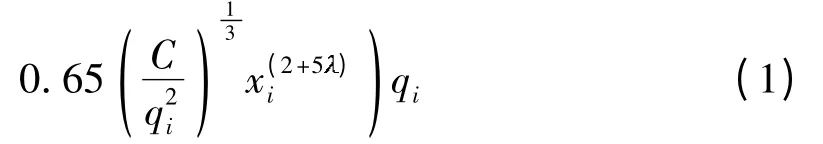
式中，n 为交叉口的总车道数，C 为交叉口的周期时长，i为对应相位的绿信比，yi为对应车道的交通流量比，xi为对应车道的交通流量饱和度，qi为对应车道的交通流量.

平均延误即为

式中，Q 为交叉口每小时总流量.

2.2 右转－前行－掉头两相位组织方式的延误计算模型

间接左转交通组织方式主要有(禁左)右转－前行－掉头和(禁左)直行－掉头两种方式.文中主要研究右转－前行－掉头方式的平均延误.

如图3 所示，当采取右转－前行－掉头的交通组织方式时，车道的组织方式也会相应变化.原有的左转专用车道，改为直行车道;由于左转车流改为右转－前行－掉头车流，使得右转流量变大. 所以，原有的最外侧直右混行车道改为右转专用车道(更为合理).配时方案也会因此作相应的变化.此时的交叉口平均延误可采取在韦伯斯特延误公式twebster的基础上增加其它部分的时间变化.

图3 右转－前行－掉头设计方案Fig.3 R-S-U design plan

原左转车辆右转直行至中央分隔带缺口处的距离L1(S1+S2+L3)所需要的时间tL1为

式中，v1为车辆通过L1距离的平均速度.

中央分隔带平均等待时间tmidwait为

式中:Qm为可插入主路的通行能力;Q 为对向可穿插车流的每小时流量;n 为道路可容纳的等候车辆数;te为对向可穿插车流可插入临界间隙(不包括掉头时间)，一般取6 ～8 s;tL2为中央分隔带处掉头时间，一般取2 ～3 s，即车速为4 ～6 m/s;tf为左转车流跟随时间，一般取3 ～5 s.

此处的可插入主路通行能力公式参考了文献［15］，并进行改进，具体推导如下:

假设出入口或次要道路最多可容纳n 辆车排队，则当主路车流间隙为t 时，有k 辆次路车流车辆进入主路(k ＜n)，对其概率pk(t)，有

则次路车流利用间隙t 进入主路的车辆数为

由于次路最多可以容纳n 辆车排队，因此当t ＞tc+ktf时，次路进入主路车辆达到最大数n，车辆数并不会随着主路的间隙t 的增大而增大. 故公式推导如下:

因此，次路车流Qm计算公式为

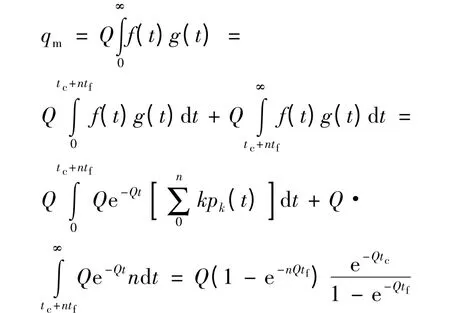
即

因为此处不是纯粹的垂直穿过对向车流，而是还需要包含车辆掉头时间，所以原有的系数tc修正为tc+tL2.

中央分隔带处掉头时间tL2为

式中:R1为车辆掉头的转弯半径，一般大于4m 较为合适;v2为车辆在中央分隔带缺口处转弯的平均车速，一般取4 ～6 m/s.

交织区域的速度Sw、Snw为

式中:a、b、c、d 为经验参数;VR为交织流量与总流量(交织流量+非交织流量)的比值;V 为总流量;N 为交通区车道数;L 为交织区域长度;Sff为自由流速度，一般为60 km/h. 交织区域速度公式参数如表1所示.

表1 交织区域速度公式参数Table 1 Parameters for weaving area speed formula

此处公式借鉴HCM2000［16］手册中高速公路交织区段中交织区域的交织车流速度和非交织车流速度求导公式，并结合交叉口的实际情况，对a、b、c、d修正得到.实践时可以结合实际交叉口情况修正或套用符合道路实际情况的公式.

交织区域的延误twL3、tnwL3为

式(12)为交织车辆(原左转车辆)行驶时间，其中L为交织区域长度. 由于交织车辆始末速度为0 m/s(在交叉口等待)，所以平均速度为平均交织速度的一半.式(13)为非交织车辆(对向车辆)的延误. 由于左转车辆掉头，会使得对向车流的车速减慢.用正常行驶时间减去实际行驶时间，即可获得对向车流的延误时间.其中，v0为对向车辆的正常行驶速度.粗略估计，可令交织车辆数为0，代入非交织平均速度公式中求得v0.

左转车辆从停车线穿过交叉口的时间tL4为

式中，车辆以匀加速a 通过交叉口，假设为2.5 m/s2.

左转车辆原方案左转通过交叉口的时间tL5为

式中，假设车辆以近似圆弧左转通过交叉口，R 为半径.

总延误计算公式如下:

总延误为在韦伯斯特总延误值的基础上，加上左转车辆右转－前行－掉头到通过交叉口的时间与原本左转直接通过交叉口的时间之差加上受到左转弯车流掉头而减速的对向车流的延误之和.

平均延误即为

式中，Q 为交叉口每小时总流量.

2.3 左转交通组织方式判决条件

结合以上对两种左转交通组织方式的分析，尤其是右转－前行－掉头方案下的交叉口整体平均延误的定量计算，得到左转交通流交通组织方式判决模型.通过这个模型，可以基于式(18)进行定量分析，确定在一定的交通情况下何种左转方式更为合理.

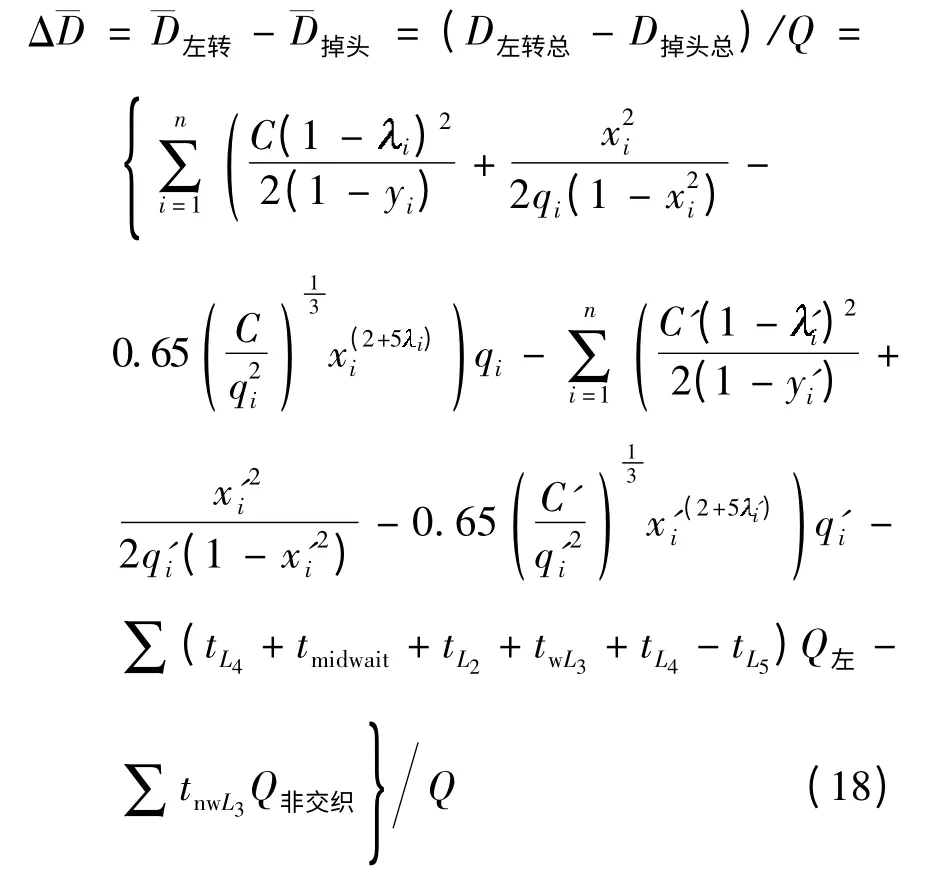
式中，第1 项为直接左转方式的交叉口整体总延误，后面3 项为右转－前行－掉头方式的交叉口整体总延误.显然，当Δ¯D ＞0 时，直接左转的交叉口整体平均延误大于右转－前行－掉头直行方式，选择后者更为合理;反之，应该设置左转专用相位.

理论分析右转－前行－掉头方式下的交叉口(如图3 所示)整体平均延误公式，可知:

(1)当东西流量不变，同时增加南北方向左转车辆流量时，原本左转车辆掉头与直接左转的行驶时间差不断累加，优势渐弱;此外，左转车辆数增加到一定的程度时，信号周期内可能无法完全通过中央分隔带，造成排队，产生较大的交通延误.

(2)当南北流量不变，同时增加东西方向总车流流量时，东西方向车流密度变大，从而左转掉头车辆在中央分隔带缺口处的等待时间陡增;同时，左转掉头车辆对东西方向的车流影响愈发变大，交叉口整体平均延误也会增加.

综上所述，间接左转只有在特定的交通条件下才优于直接左转.通过左转交通流交通组织方式判决模型，就可以科学合理地选择左转方式.

3 算例与结果分析

选取一个典型的十字交叉口(如图3 所示)研究直接左转和右转－前行－掉头两种交通组织方式的交叉口平均延误.其中涉及到的一些配时、公式参数可能会由于不同的交通参考理论而有所差异.

3.1 交叉口平均延误指标计算

对相关数据解释如下:

①交叉口车流量数据如表2 所示.

②交叉口每条车道宽度为4 m.东西方向双向6车道，南北方向双向8 车道;

③停车线到中央分隔带100m.设定最多可能容纳6 辆汽车(即式(5)中的n =6)等待;车辆掉头满足标准半径4 m.图3 中具体数据如下:

④加速度根据实际情况设为2.5 m/s2.

⑤由于车辆接近交叉口(约100 m)会减速，设由30 km/h 开始减速;

⑥假设左转饱和流量为1600 辆/h，其余方向饱和流量为1800 辆/h.

表2 交叉口车流流量Table 2 Traffic flow of the intersection

针对两种方案的具体情况配时，再计算交叉口的平均延误.具体的计算结果如表3 所示.

表3 左转和右转－前行－掉头方案的分析结果Table 3 Analysis results of direct left-turn design and R-S-U design

由此可见，采取右转－前行－掉头方式会使得交叉口信号周期大大缩短，平均延误也有效减少.

3.2 敏感性分析

为了进一步研究在不同情况下两种方案的优劣，文中提出两种利用理论公式的比较方案.

(1)采取东西流量不变、同时增加南北方向左转车流量的方案.计算结果如图4 所示.

图4 左转流量－延误图Fig.4 Relationship between left-turn traffic volume and average delay

通过采取右转－前行－掉头的交通组织方式，减少了其他相位车辆的等待时间，从而，有效减少了交叉口的平均延误. 但是，随着左转车辆的不断增加，其延误累积变大;甚至会造成车辆排队.从而，右转－前行－掉头方案的优势会削弱.

(2)采取南北流量不变、同时增加东西方向车流量的方案.计算结果如图5 所示.

图5 对向流量－延误图Fig.5 Relationship between opposition-direction traffic volume and average delay

图中，右转－前行－掉头方案平均延误均小于直接左转方案.但实际上，当流量不断增加，左转车辆在中央分隔带处等待增加，甚至造成车辆排队.交叉口延误也会发生变化.此时泊松分布不再吻合，从而等待时间骤增. 案例中，当流量增加到1.8 倍时，一个周期内，左转掉头车辆在中央分隔带处最大等待时间大于一个周期，即，掉头车辆无法全部通过中央分隔带.这会导致左转车辆在中央分隔带处不断排队，产生交通瓶颈，即此时右转－前行－掉头方案失效.采取左转方案较为合理.

以上两种比较方案得出的结果与2.3 节中理论分析的结果一致.可见，左转交通流交通组织方式判别模型具有充分的理论可行性.

3.3 理论延误模型与仿真结果比较

文中采用仿真软件VISSIM 进行方案可行性的验证.根据实际交通情况拟合后的仿真参数如下表4 所示.

表4 标定参数Table 4 Calibration parameters

首先，比较左转三相位方案下的理论与仿真结果，如图6 所示.由图可知整体拟合较好.

图6 左转理论延误与仿真延误比较图Fig.6 Comparisons between theoretical delay and simulation delay for left-turn

然后，比较右转－前行－掉头两相位方案下的理论与仿真结果，如图7 所示.右转－前行－掉头方案下的交叉口延误与仿真结果比较图前半部分(2.2倍)拟合较好，后半部分仿真结果与理论结果差距较大，这符合实际情况，即可插入间隙车流模型是在一种理想状况下建立的，它假设在泊松分布的情况下，车流不会对对向车流产生影响.但事实上，如3.2 节提到的，左转车流增加后对对向车流影响会骤增，自身等待时间也会增加，且造成排队现象，如图8 所示.

图7 掉头理论延误与仿真延误比较图Fig.7 Comparisons between theoretical delay and simulation delay for U-turn

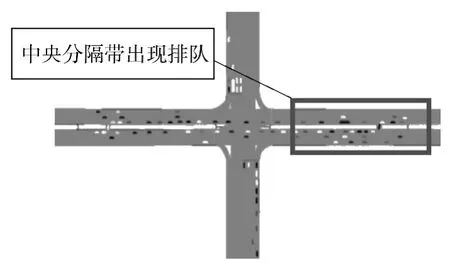
图8 中央分隔带缺口处拥堵图Fig.8 Congestion at the median openings

图7 中，当左转车辆数增加到2.2 倍，会出现延误突变点.分析如下:选取南北进口道中，左转流量较小的北进口道为例(因为，当左转流量较小的北进口道开始在中央分隔带缺口处出现排队，则左转中流量较大的南进口道更容易出现排队现象). 按照文中的取值，tf取3，tc取6，tL2取2.5，代入式(5)，得到最大可穿插流量为314 辆/h.结果介于北进口道左转流量311 辆/h(2.1 倍)与325 辆/h(2.2 倍)之间.加之每个周期左转流量的波动，所以，当左转流量到达2.2 倍时，将会产生掉头排队现象，并影响其它车道车辆的正常通行.

同时，南北掉头车辆一个周期内未全部通过，东西方向车辆排在掉头车辆后面等待，延误也会因此累积增加.所以，此时的中央分隔带等待时间公式还需要进一步做专题研究.

直接左转和右转－前行－掉头方案的仿真比较结果如图9 所示.

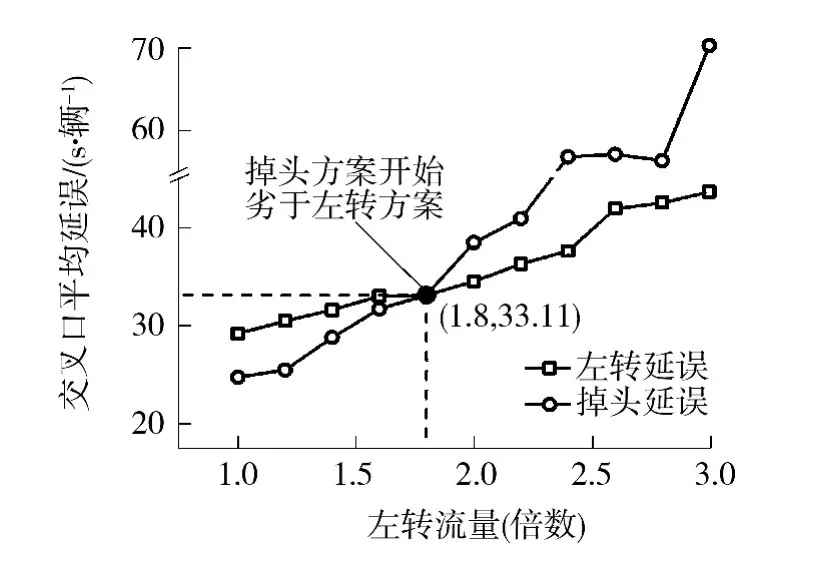
图9 左转流量－延误仿真图Fig. 9 Relationship between magnification times of left-turntraffic volume and average delay in the simulation

尽管直到后半部分(大于2.2 倍)右转－前行－掉头交叉口平均延误才会陡增.但是事实上，当左转流量增加到原先的1.8 倍时，两种方案下的交叉口平均延误就已经十分接近;当左转流量增加到原先的1.9 倍时，设置左转专用相位方案就优于右转－前行－掉头方案.这与之前3.2 节得出的结果吻合.

综上所述，理论计算与计算机仿真结果基本一致，所提出的模型具有较高的准确度和可靠性.

4 结语

文中通过分析禁左右转－前行－掉头车辆的整个行驶过程，获得整个交叉口的平均延误公式，提供一种定量比较两种方案优劣的方法. 当左转弯流量增加到一定程度时，禁左掉头右转的方案不再有优势.因而，此时设置左转专用车道和专用相位更为合理.当对向的流量十分大时，左转车辆在中央分隔带的等待时间会大大增加，甚至造成排队情况;同时，对于对向车流的影响也会加剧. 此时也适宜设置左转弯专用相位.文中旨在提供一种比较两种交通组织方式的建模思路.其中，各部分的计算公式还有待通过大量的实测数据去进一步完善.

［1］王殿海，付凤杰，蔡正义，等. 基于排队最远点约束的最大周期时长优化方法［J］.华南理工大学学报:自然科学版，2014，20(5):67-74.Wang Dian-hai，Fu Feng-jie，Cai Zheng-yi，et al. Optimization method of maximum cycle length based on back of queue［J］.Journal of South China University of Technology:Natural Science Edition，2014，20(5):67-74.

［2］Chowdhury M，Derov N，Tan P，et al.Prohibiting left-turn movements at mid-block unsignalized driveways:Simulation analysis［J］. Journal of Transportation Engineering，2005，131(4):279-285.

［3］Access management manual (2003)［R］.Washington D C:National Research Council，2003.

［4］刘博，吴海兵，江浩，等. 十字信号交叉口左转远引掉头组织方式及影响分析［C］∥第四届湖北省土木工程专业大学生科技创新论坛论文集. 湖北:华中科技大学出版社，2011:106-110.

［5］Zhou H，Lu J，Yang X，et al.Operational effects of U-turns as alternatives to direct left turns from driveways ［J］.Transportation Research Record，2002，50(1):72-79.

［6］Zhao Rong-long，Fan Jing-jing，Liu Pan.Selection of optimal U-turn locations for indirect driveway left-turn treatments on urban streets［J］.Journal of Southeast University，2010，26(4):628-632.

［7］Guo T，Liu P，Lu J J，et al. Procedure for evaluating the impacts of indirect driveway left-turn treatments on traffic operations at signalized intersections ［J］. Journal of Transportation Engineering，2011，137(11):760-766.

［8］刘书鹏，马骏.路段掉头交通流组织方式研究［J］.交通运输系统工程与信息，2007，7(2):124-128.Liu Shu-peng，Ma Jun. Application of median U-turn in traffic organization［J］.Journal of Transportation Systems Engineering and Information Technology，2007，7(2):124-128.

［9］Zhou H，Hsu P，Lu J J，et al. Optimal location of U-turn median openings on roadways ［J］. Transportation Research Record:Journal of the Transportation Research Board，2003，1847(1):36-41.

［10］张宁，陈恺，高朝晖，等.基于微观仿真的远引掉头选址规划方法［J］.交通运输工程学报，2008，8(1):78-82.Zhang Ning，Chen Kai，Gao Zhao-hui，et al.Site planning method of U-turn followed by right-turn based on microsimulation［J］.Journal of Traffic and Transportation Engineering，2008，8(1):78-82.

［11］朱锐，李林波，吴兵.基于VISSIM 仿真的交叉口间接左转适应性研究［J］.交通科技，2011，37(5):96-99.Zhu Rui，Li Lin-bo，Wu Bing.Study of the adaptability of indirect left-turning at the intersection based on vissim simulation［J］. Transportation Science ＆ Technology，2011，37(5):96-99.

［12］冷军强，冷雨泉，张亚平.基于VISSIM 仿真的交叉口远引式左转掉头位置的研究［J］. 昆明理工大学学报:理工版，2009，34(3):56-59.Leng Jun-qiang，Leng Yu-quan，Zhang Ya-ping.Location research of indirect left U-turn at intersection based on VISSIM simulation［J］.Jouranal of Kunming University of Science and Technology:Science and Technology，2009，34(3):56-59.

［13］王钊，张卫华.可调头交叉口交通延误分析与仿真研究［C］∥第三届中国智能交通年会论文集.南京:东南大学出版社，2007:283-287.

［14］Yang X K，Zhou H G. CORSIM-based simulation approach to evaluation of direct left turn versus right turn plus U-turn from driveways［J］.Journal of Transportation Engineering，2004，130(1):68-75.

［15］广州至信交通顾问有限公司. 基于智能交通检测数据的车型换算系数研究及通行能力研究［R］.广州:至信交通顾问有限公，2013:88-98.

［16］Highway capacity manual (HCM)2000［R］.Washington D C:National Research Council，2000:888-895.