城市轨道交通快慢车停站方案优化*
王智鹏 罗霞
(西南交通大学 交通运输与物流学院,四川 成都610031)
道路交通拥堵频发及低碳经济的要求,迫切需要城市轨道交通不断提升吸引力与覆盖率,多样化高覆盖率是其客运服务之关键所在. 快慢车组合作为独特的运营模式,是提升其客运服务水平的一项高效措施[1].国外轨道交通发展成熟的城市(如纽约、东京等)的多条线路已采用快慢线组合模式.我国各特大城市轨道交通经过多年的发展已形成一定规模,但在快慢车组合方面均有所欠缺,需要对包含于网络的线路从需求特征、建设条件等进行研究分析,选择合理的越行区段、站点,并对行车组织效果进行评估,以保证快慢线的运营可行可操作.
较早研究该问题的学者是Salzborn[2],此后大多研究将快慢车组合问题与停站方案、列车运行图优化等问题合并进行研究.Renfrew[3]为适应不同时段客流特性,采用了基于不同速度的轻轨运营成本效益模型,计算并提出高峰、平峰时段的快慢车开行优化方案. Suh 等[4]采用仿真手段以首尔地铁5 号线为对象,研究了既有站站停模式与采用快慢车组合模式下各运营指标的优劣,指出若不考虑快慢车组合引起的固定投资增加,合理的快慢车组合模式更有效率.Garzon 等[5]通过开发的城市轨道交通运行图铺画软件,输入列车ATO (列车自动驾驶子系统,Automatic Train Operation Systems)曲线和停站方案,自动调整始发站列车发车间隔,自动铺画了快慢车线路列车运行图.孔宪娟[6]运用元胞自动机模型探讨快慢组合列车追踪特性,分析了发车间隔时间、停站时分及站后安全防护段等对列车追踪运行和延迟时间产生的影响,给出了快慢车组合结构与总平均延迟时间的作用机理. 祝晓波[7]针对轨道交通市域线郊区部分,以节省乘客时间最多为起点,研究线路的最佳停站方案,并以此铺画运行图,比较了不同快慢车组合对数的使用条件. Mignone 等[8]基于线路各车站列车时刻表稳定的情形,建立优化模型生成了不同时段快慢车跨站组合,使运输服务满足线路各车站不均衡旅客乘降量. 陈晓峰 针对上海轨道交通16 号线在使用快慢车组合后造成的通过能力下降、运营难度加大等问题,通过分析快慢车运行方案,比对通过能力、行车组织方案等,对该线近期快慢车方案提出建议.
当前快慢车停站方案的研究主要呈现以下特点:①行车组织优化模型所占比例较大,复杂程度高,实用性不强;②大多对问题进行了一定程度从简处理,一些直接以停站类型为模型或仿真的输入条件;③大多以客流需求为单一要素进行优化求解.
然而城市轨道交通具有公私兼有属性,快慢车停站问题研究与经济社会活动密切相关,在进行优化时不仅要考虑客运需求的表达、基础设施条件和行车组织可行性等问题,还要考虑城市交通发展战略、车站在城市公共交通网络中的作用等方面.
基于以上分析,文中在汲取之前学者在快慢车问题研究成果的基础上,以属性优势分析粗糙集定权灰色分级模型为出发点,对车站进行合理分级,构建基于车站分级的城市轨道交通快慢车停站方案优化模型,并应用遗传退火算法求解问题.
1 基本问题
当前城市轨道交通快慢车停站方案的确定主要以客流分析为主要影响因素,很少涉及或忽略站点区位、路网中的作用及线路运营特性等重要因素,优化后的停站方案主要是大客流站点,而对于其在网络中的作用以及在城市经济社会发展过程中的公益性作用等将无法涵盖,生成的停站方案与线路技术特性不符,实效性较差. 为解决该问题,文中将快慢车停站方案优化问题定义为:在列车开行线路技术特性和通过能力一定条件下,满足客运服务、换乘衔接等约束的列车停站与否以及快慢车组合结构的0 -1优化问题.用N 表示线路允许总发车次数,Ne表示快车开行数量,列车运行的停站序列不确定,受车站分级结果影响,作为问题的未知条件,用决策变量xi表示列车在第i(i=1,2,…,n)个车站是否停站(是则取1,否则为0),由此将问题转成求解满足一定目标和约束的xi问题.
2 站点分级方法
2.1 灰色聚类
以线路上n个车站为聚类对象,车站日均客流量、日均高峰小时客流量、周边业态数(600 m 半径范围内大型商业场所、居住区和交通车站数)、换乘衔接线路数、公共属性(600 m 半径范围内政府机构数)、线路技术特性(是否为联锁站、出入场站和折返站,是取为1,否则为0,并求和)以及车站流通能力(由出入口数及AFC 设备数量构成)为m个聚类指标,一、二、三级为s个不同灰类,按照第k(k =1,2,…,n)个对象关于l(l=1,2,…,m)个指标观测值ykl将各对象聚类到第r(r∈{1,2,3})个灰类[10].设定各子类r 的白化权函数标记为为l 指标关于各子类r 的权,分为变权与定权,为变权时:

式中,rl 为l 指标的r 子类临界值,根据具体白化权函数确定,主要有以下3 种计算形式:

对象k 关于指标l 的样本值ykl的灰色变权聚类系数的算式为

2.2 属性优势分析粗糙集
(1)决策表生成
车站各年份的分级结果为对象U,各年份各指标值为条件属性C,车站各年份的分级结果的灰类属性为决策属性D,形成车站分级决策表,从而得到车站分级的知识系统S =(U,A,V,f),式中A 为属性集,V 为属性值域,f:U×A→V 是一个信息函数.
(2)数据离散化
车站分级决策表中决策属性是各年份车站分级情况灰类属性,故不用对决策属性再做数据离散化处理.而对于作为条件属性的车站各年份各指标,对l 指标的r 子类的临界值进行数据离散化处理.
(3)约简算法
对于车站分级决策表中条件属性及决策属性包含的偏好信息,文中条件属性的偏好信息由高到低涵盖一、二、三、四级4 类;决策属性的偏好信息由高到低包括一、二、三级3 类.根据决策属性,车站分级将分偏好顺序类3个:Cθ1={三级},Cθ2={二级},Cθ3={一级}.按照偏好决策类划分论域,即可得到以下决策类的并集:,分级结果为三级;Cθ1∪Cθ2,分级结果至多为二级;∪Cθ3,分级结果至少为二级;=Cθ2,分级结果为一级. 式中表示分级结果至多为某种等级,表示分级结果至少为某种等级.
采取合理的约简算法如遗传算法等,可搜索到一定规模的属性约简,包括属性最少且属性出现频率最高的约简则为最满意的约简,车站分级时,可直接使用这些影响因素进行,其他因素影响则可忽略,降低计算复杂性,提升分级准确度.
(4)约简属性优势分析
分析约简后的属性,求出各条件属性和决策属性间的灰色相对关联度[11-14],对约简后的条件属性集进行优势分析,并依据灰色关联度进行数据归一化处理即可得到灰色定权聚类权重值.
2.3 站点分级方法流程
站点分级方法流程如下:
(1)因首末站列车必须停车,直接将其划分为一级车站;
(2)将其余车站的各指标数值生成区间值像,应用灰色变权聚类模型对其进行预分级;
(3)应用预分级结果生成分级决策表,并进行数据离散化处理;
(4)应用遗传算法得到最满意约简,求出约简后所得的各条件属性与决策属性之间的灰色关联度,确定灰色聚类权重值;
(5)根据原始数据,应用灰色定权模型进行车站分级.
3 模型构建
3.1 假设条件
为便于建模分析,设定假设如下:①车辆技术参数相同;②只考虑单向列车运营;③列车运行交路单一,编组唯一;④列车只有快慢之分,不考虑直达、特快等更详细划分;⑤主要由停站时间及起停附加时间影响快慢车旅行时间差;⑥快车在车站越行慢车;⑦若旅客出行起讫点均被快慢车站点覆盖,只有当旅客选择快车出行总时间超过慢车出行总时间时,才考虑二者之间竞争关系;⑧考虑到换乘造成的不便性,只有当乘客出行的起止点有一个为快车站,且当考虑换乘惩罚系数(文中取为1.6[15])的选择换乘的出行时间小于慢车出行时间时,才发生快慢车间换乘,否则采用直达方式.
3.2 目标函数
1)参数及变量定义
设参数如下:S,车站集合;S1i,线路首车站到乘客出行路径起始站所覆盖的车站集合;Sjn,乘客出行路径终点站到线路末车站所覆盖的车站集合;R1、R2、R3,分别为一、二、三级车站集合,R1∪R2∪R3=,分别表示一、二、三级车站是否停车,停车取为1,否则为0;ηij,车站i 至j 间的客流量、,分别代表车站i 至j 间的快、慢车客流量,由直达客流及换乘客流构成[16];α1、α2,车辆最小、最大载客能力;tij,车站i 至j 区间纯运行时分;,站站停方案列车在车站i 停站时间,快、慢车在车站i 停站时间,一般由旅客乘降量综合确定;tssi ,列车在车站i 的起停附加时分;T,优化时段长度;c1,车辆固定成本;c2,列车每公里的运行成本;c3,列车每一次停站的成本;L,线路长度;Ns,慢车各自发车次数;I,站站停方案时列车发车间隔[17];I1、I2;快、慢车各自发车间隔;T1、T2,快、慢车各自周转时间;,首、末站列车折返时间.
2)由于城市轨道交通具有公私兼营特性,在提升服务水平的同时,需要尽力追求低的生产成本,从而实现城市轨道交通系统整体效益最大化. 由此构建目标函数如下.
(1)只有当快慢车组合方案能够引起旅客总出行时间减少时,即站站停方案旅客总出行时间Ts与快慢车方案旅客总出行时间Tes之差ΔT=Ts-Tes≥0,才考虑开行快慢车,因此将优化目标定义为:求ΔT 最大;另由于站站停方案开行计划确定后旅客总出行时间也将为已知值,可将优化目标简化为快慢车方案旅客总出行时间最少.
根据定义,站站停方案旅客总出行时间为

快慢车方案旅客总出行时间由候车时间、车上时间和停站时间构成,具体形式如式(5)所示.接着根据运营计划编制实效性目标,设定以下原则:一级车站、首末站快车必须停车,二级车站快车根据优化需要停车,三级车站快车不停车,且由于I1=T/Ne,I2=T/Ns,可将式(5)简化为式(6).

(2)企业运营成本最小
企业运营成本C 主要由车辆固定成本、运营可变成本和停站附加成本三方面构成[18].车辆固定成本由优化时段内为满足快慢车组合方案运营需要的车底数来确定,运营可变成本与列车运行公里数相关,停站附加成本是由进出站列车起停而产生,因此,优化目标表示为

3.3 约束条件
(1)0 -1 变量约束:

(2)开行快车条件约束:

(3)快车车辆满载约束:

(4)慢车车辆满载约束:
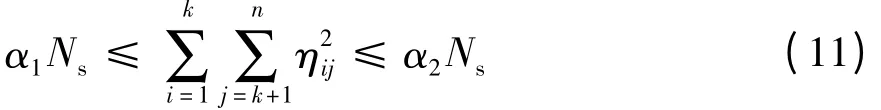
(5)旅客直达约束:

(6)通过能力约束:

4 实例求解与分析
4.1 线路概况
某城市轨道交通线路有车站15 座,线路全长79.36 km,全程区间纯运行时分50 min,列车均为6节编组,全部采用B 型车,定员240 人. 表1 为各聚类指标取值情况;表2 为OD 矩阵表;表3 为列车在各区间运行时分;表4 为模型所需设定的各参数取值.
4.2 车站分级
(1)首先将车站2 ~14 各指标值生成区间值像,构建白化权函数,应用灰色变权聚类模型进行预分级,生成决策属性D,并对评价决策表中条件属性进行离散化处理;
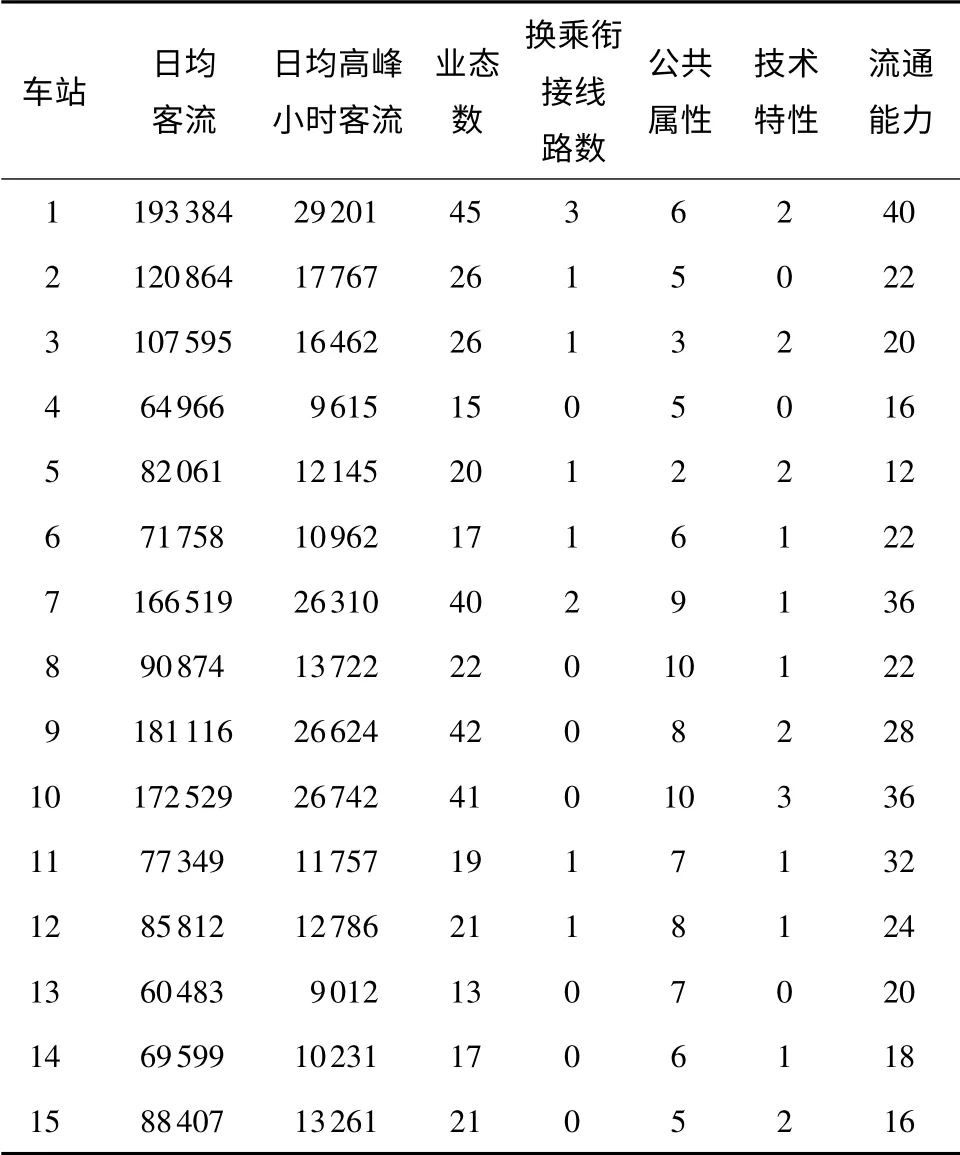
表1 车站各聚类指标取值Table1 Clustering index values for the station

表2 OD 矩阵表Table 2 OD matrix of passengers

表3 区间运行时分Table 3 Train running time of section

表4 模型中各参数取值Table 4 Values of the parameters in the model
(2)参考文献[19]中车站等级临界值,将各条件属性划分为一、二、三、四级4个等级,生成偏好决策表,如表5 所示;
(3)利用遗传算法搜寻偏好决策表中条件属性约简,得到约简为{日均高峰小时客流量,换乘衔接线路数,公共属性,技术特性,流通能力},因此在车站分级时直接利用这5个影响因素来进行,不考虑其他因素的影响;
(4)由于表5中的决策属性为定性指标,因此在确定各条件属性与决策变量的灰色相对关联度时需将其定量化,文中通过对所有条件属性的灰色变权白化权函数转折点取均值进行确定,由于其均值在0.11 ~0.53 的范围内浮动,可采用二极比例方法进行定量化.基于条件属性分布特征,决策属性为三级时取值为0.11,二级为0.32,一级为0.53,从而得到各条件属性和决策属性的灰色相对关联度,如表6 所示.

表5 车站分级偏好决策表Table 5 Preference decision table of the station classification

表6 灰色相对关联度及权重Table 6 Grey relative relational degree and weight
(5)对关联度进行归一化处理,可得到灰色定权聚类的权重值见表6,由此可将各车站进行分级,最终结果如表7 所示.

表7 车站分级结果Table 7 Classification results of stations
4.3 模型求解与分析
使用混合遗传模拟退火算法[20-22]和Matlab 语言编程求解算例,具体操作如下:
步骤1:设初温Te为1500,退温速度θ 为0.9,k=0;步骤2:采用随机方法,生成初始种群,采用0,1 编码,染色体由停站状况、快车次数Ne及慢车次数构成;停站状况染色长度为二级车站数,其中“1”表示在该二级车站停车,“0”则表示不停车;Ne、Ns采用随机方法编码,解码后二者之和不大于通过能力N;步骤3:采用模糊理论无量纲化处理两个不同量纲的目标函数,并运用伸缩指标及权重系数来体现两目标函数的重要程度[23];步骤4:进行收敛准则及可行性判断,若满足,转步骤9;否则,转步骤5;步骤5:随机选择个体与当前种群中最优个体交叉产生新个体,新个体适应度值若大于当前最优解,进行更新,否则存储当前最优解至记忆器;步骤6:对变异操作全部个体,划分保留的最佳个体为n个子种群,为模拟退火算法初始种群,更新种群和记忆器,保存最优状态和温度调节参数;步骤7:对n个子种群的个体执行定步长抽样模拟退火操作,以概率min[1,exp(-ΔE/tk)]接受后代,更新种群及记忆器.步骤8:执行退温操作tk=0.9tk-1,转步骤4;步骤9:输出此次优化结果;步骤10:是否满足收敛准则,若是则输出最终优化解;否则转步骤2.
使用上述算法,经过多次计算试验,种群遗传79 代后收敛到最优解,与不使用车站分级直接优化至156 次得到最优解相比,在同样的计算机配置下,文中在最优解误差为0.799%的情况下将优化时间缩减了近60%,时效性较强,最优解见表8.此外,通过对优化过程进行分析发现,不仅快慢车总发车次数停站方案的优化具有重要的影响,而且快慢车比例结构对于停站方案的优化也会产生重要的影响,分析图1,当快慢车比例由16∶6 向10∶16(其余比例为非可行解)变化时,综合值随慢车所占比例的增大先下降后上升,在快慢车比例结构为12∶10 时,其值达到最小,旅客出行总时间也出现基本相似的变化趋势.而企业运营成本则随着慢车次数的增加而逐渐上升,这是由于慢车次数的增加导致停站次数增加和列车周转时间延长的原因,反之也说明增加快车开行数量有助利于降低企业运营成本.

表8 快慢车停站方案最优解Table 8 Optimal solutions of express/local train stopping schedule

图1 快慢车比例对停站方案优化的影响Fig.1 Ratio influence of express/local on stopping scheme
5 结论
文中应用约简算法对影响车站分级的各因素进行属性约简,实例分析得到车站分级主要需要考虑日均高峰小时客流量、换乘衔接线路数、公共属性、技术特性、流通能力5个因素,在此基础上,采用约简属性优势分析确定各条件属性与决策属性的灰色相对关联度,从而使用灰色定权聚类模型对车站进行合理分级.
相较于其他优化方法,通过设定不同等级车站列车停站原则,降低模型求解复杂度,可将解空间由2nN缩小至2i2N个,求解效率得到了较大提高,对快速地制定列车运营方案具有重要意义.
分析适应度函数变化情况发现,不仅快慢车总发车次数对停站方案优化具有重要的影响,快慢车比例结构对于停站方案优化也会产生重要的影响,分析表明快车开行数量的增加将有助于企业运营成本的降低,即停站成本与列车车底数的降低.
[1]狄迪,杨东援. 基于快慢车组合的城市轨交走廊客流分析模型[J].同济大学学报,2014,42(1):78-83.Di Di,Yang Dong-yuan. Passenger flow analysis model about express/slow train in urban rail transportation corridor[J].Journal of Tongji University,2014,42(1):78-83.
[2]Salzborn E M.Timetables for a suburban rail transit system[J].Transportation Science,1969(3):279-316.
[3]Renfrew R M. Technology selection and development for an intermediate capacity transit system[C]∥Prceedings of Conference Record-IAS Annual Meeting (IEEE Industry Applications Society). New York:Institute of Electrical and Electronics Engineers,1977:939-945.
[4]Suh W,Chon K S,Rhee S M.Effect of skip-stop policy on a Korean system [J]. National Research Council,2002(2):33-34.
[5]Garzon N J,Sanz B J D D,Gmerz R J,et al.A new tool for railway planning and line management[J].WIT Transaction on the Built Environment,2008,103:263-271.
[6]孔宪娟.基于元胞自动机的交通流建模及其特性分析研究[D].北京:北京交通大学交通运输学院,2007.
[7]祝晓波.市域轨道交通快速线开行方案研究[D]. 成都:西南交通大学交通运输与物流学院,2009.
[8]Mignone A,Accadia G. Operations research models for programming support of cadenced timetables[J].Ingegneria Ferroviariav,2010,65(1):9-29.
[9]陈晓峰.上海轨道交通16 号线快慢车运行方案研究[J].城市轨道交通研究,2014(5):68-72.Chen Xiao-feng.On express/slow train operation program on shanghai rail transit line 16[J].Urban Mass Transit,2014(5):68-72.
[10]刘思峰,杨英杰,吴利丰,等.灰色系统理论及其应用[M].北京:科学出版社,2014.
[11]郑晓峰,王曙.基于粗糙集与关联规则的道路运输管理信息数据挖掘方法[J].华南理工大学学报:自然科学版,2014,42(2):132-138.Zheng Xiao-feng,Wang Shu.Data mining method of road transportation management information based on rough set and association rule[J].Journal of South China University of Technology:Natural Science Edition,2014,42(2):132-138.
[12]张蕾,王高旭,罗美蓉. 灰色关联分析在水质评价应用中的改进[J]. 中山大学学报:自然科学版,2004,43(6):234-236.Zhang Lei,Wang Gao-xu,Luo Mei-rong. Application of an improved grey association analysis method in water environmental quality assessment[J].Acta Scientiarum Naturalium Universitatis Sunyatseni,2004,43(6):234-236.
[13]Gu H,Song B F.Study on effectiveness evaluation of weapon systems based on grey relational analysis and TOPSIS[J].Journal of Systems Engineering and Electronics,2009,20(1):106-111.
[14]Xie N M,Liu S F. Research on evaluations of several grey relational models adapt to grey relational axioms[J]. Journal of Systems Engineering and Electronics,2009,20(2):304-309.
[15]叶臻,关宏志.城市轨道交通枢纽换乘供需一致性研究[J].北京工业大学学报,2014,40(4):542-548.Ye Zhen,Guan Hong-zhi. Study on the consistency between supply and demand on terminals of urban rail transit network[J].Journal of Beijing University of Technology,2014,40(4):542-548.
[16]张永生,姚恩建,代洪娜. 成网条件下地铁换乘量预测方法研究[J].铁道学报,2013,35(11):1-6.Zhang Yong-sheng,Yao En-jian,Dai Hong-na. Transfer volume forecasting method for the metro in networking conditions[J]. Journal of the China Railway Society,2013,35(11):1-6.
[17]许旺土,何世伟,宋瑞,等.整合运营下的轨道交通发车间隔及票价模型[J]. 系统工程学报,2011,26(3):330-339.Xu Wang-tu,He Shi-wei,Song Rui,et al. Headway and fare model of urban rail transit for integrated operation[J].Journal of Systems Engineering,2011,26(3):330-339.
[18]胡俊.城市轨道交通运营成本研究[D]. 北京:北京交通大学经济管理学院,2007.
[19]陈扶崑,吴海军.基于定量分析的城市轨道交通车站分级探讨[J].现代城市轨道交通,2010(3):78-81.Chen Fu-kun,Wu Hai-jun. Study on classification the urban Rail stations based on the quantitative analysis[J].Modern Urban Transit,2010(3):78-81.
[20]杨庆芳,梅朵,郑黎黎,等.基于云计算的城市路网最短路径遗传算法求解[J].华南理工大学学报:自然科学版,2014,42(3):47-52.Yang Qing-fang,Mei Duo,Zheng Li-li,et al.Cloud computing-based genetic algorithm to solve the shortest path in urban road networks[J].Journal of South China University of Technology:Natural Science Edition,2014,42(3):47-52.
[21]王晓圆,王爱民,范瑞成,等.基于遗传算法的配作齐停类调度约束处理技术[J].计算机集成制造系统,2014,20 (11):2788-2797.Wang Xiao-yuan,Wang Ai-min,Fan Rui-cheng,et al.Matching and same time stop scheduling constraint processing technology based on genetic algorithm[J].Computer Integrated Manufacturing Systems,2014,20 (11):2788-2797.
[22]蓝海,王雄,王凌. 复杂函数全局最优化的改进遗传退火算法[J]. 清华大学学报,2002,42(9):1237-1240.Lan Hai,Wang Xiong,Wang Ling.Improved genetic annealing algorithm for global optimization of complex functions[J]. J Tsinghua Univ,2002,42(9):1237-1240.
[23]王彩华,朱嫂东.多目标优化的模糊解法中目标权重的处理方法[J].重庆大学学报,1992,15(6):92-97.Wang Cai-hua,Zhu Yu-don.A processing method for the weight of the object in the fuzzy solving method for the multi-objective optimization [J]. Journal of Chongqing University,1992,15(6):92-97.

