基于自适应变步长电阻增量法的最大功率点跟踪*
陈渊睿 周东宝 许志荣 李晨迪 曾君
(1. 华南理工大学 电力学院,广东 广州510640;2. 华南理工大学 广东省绿色能源技术重点实验室,广东 广州510640)
太阳能作为一种新型绿色能源,可解决因常规能源枯竭而引发的能源危机,受到国内外的广泛关注,光伏发电是当前利用太阳能的主要形式之一.由于光伏电池的输出具有较强的非线性特征,它的输出功率不仅与光伏电池内部特性有关,还受到外界环境条件(光照、温度)的影响,采用最大功率点跟踪技术可有效提升光伏系统的能量转换效率[1-2].
常用MPPT(Maximum Power Point Tracking)方法中开路电压系数法和短路电流系数法[3-6]控制简单易于实现,但需要周期性断开或短路光伏电池板,使得能量损失较大,且该方法的系统工作点并不是真正的最大功率点. 扰动观察法[7-10]是目前研究和应用最广泛的MPPT 方法,它通过对光伏板的输出电压施加扰动,检测输出功率的变化来跟踪最大功率.其优点是控制策略简单,易于实现,对参数检测精度要求低,在外界环境比较稳定的情况下有较好的控制效果.但是该方法需要不断地对参考电压施加扰动来判断最大功率点,由此不可避免地会造成功率振荡;同时,当外界环境剧烈变化时,还会导致最大功率点跟踪方向错误,严重时甚至引起电压崩溃,系统出现严重振荡现象. 电导增量法[11-17]的控制思想与扰动观察法类似,通过比较光伏电池的电导增量和瞬间电导来改变系统的控制信号. 对于传统定步长算法,选用较大的扰动步长可获得较高的动态响应速度,但稳态功率损失较多;较小的扰动步长可减少稳态功率损失,但系统响应速度较慢.文献[11]中提出一种基于功率对电压微分(dP/dU)的变步长算法,系统工作点远离最大功率点时扰动步长较大,越靠近最大功率点扰动步长越小.该方法可以很好地兼顾系统稳态和动态性能,但是在光照剧烈变化的情况下系统响应速度变慢,并出现功率振荡现象,从而导致功率损失增多.
为使光伏系统在光照剧烈变化条件下仍然可以保持较快的响应速度和较高的稳态精度,提出一种自适应变步长电阻增量法. 文中首先分析了传统变步长算法在光照剧烈变化情况下稳态和动态性能变差的问题,然后详细介绍了自适应变步长电阻增量法的工作原理,在Matlab/Simulink 中建立光伏系统的仿真模型进行仿真分析,最后搭建基于DSP(TMS320F28035)控制的5 kW 光伏系统实验平台,通过实验验证了所提算法的有效性.
1 变步长算法
传统定步长算法扰动步长的选取会引起响应速度与稳态精度之间的矛盾,变步长算法通常是在电导增量法的基础上用功率对电压的微分(dP/dU)来代替定步长扰动,并引入速度因子N 来保证算法的收敛性,步长更新规则为

式中,D(k)为k 时刻变换器的占空比. 速度因子N的选取会直接影响控制算法的性能,文献[11]中给出了一种确定N 值的简单方法,即N 必须满足下式:

式中,ΔDmax为最大占空比扰动步长. 当算法满足式(2)时,系统工作于变步长模式;否则,系统以扰动步长ΔDmax运行于定步长模式.该控制策略同样适用于参考电压扰动的情形,详见文献[9]所提算法.
但该算法中最大扰动步长ΔDmax和速度因子N一旦选定就无法改变. 如图1 所示,功率P1远大于功率P2. 对选定的速度因子N1和最大扰动步长ΔDmax1,在功率P1对应的光照强度下算法跟踪性能良好,但光照突然下降到功率曲线P2对应的水平时,系统几乎全部运行于变步长模式,这就会大大降低系统的启动速度和动态响应速度.速度因子N2和最大扰动步长ΔDmax2可使得功率曲线P2快速稳定跟踪最大功率点,而当光照突然升高到功率曲线P1对应的光照强度,功率曲线P1则几乎无法运行于变步长模式,引起功率振荡,降低了系统的输出功率.对文献[9,11]所提变步长算法,很难找到一组最优的速度因子和最大扰动步长能同时满足光照剧烈变化条件下最大功率跟踪需要,即存在跟踪“死区”.文献[12]中提出一种改进型变步长电阻增量法,利用步长分界函数(I 为电流)在最大功率点两侧各有一个极值点的性质,将两个极值点中间区域设定为变步长区域,调整步长的速度因子选为工作点落在极值点两侧时,系统运行在定步长模式.该方法在光照剧烈变化时保持良好的动态跟踪速度和稳态精度,但是该算法选取步长分界函数数值较大且需要进行多次微分运算才能判定分界点,算法计算量较大;速度因子整定公式未能充分利用分界函数且有较强的非线性,同样增加了计算量;选取初始扰动步长时没有考虑最大功率点两侧不同的输出特性.文献[13]中提出一种基于短路电流系数法的新型扰动观察法,结合短路电流系数法的自适应控制策略能使系统工作点快速逼近最大功率点,当工作点在最大功率点附近时,利用基于参考电流扰动的扰动观察法来跟踪最大功率点.该方法可以在光照剧烈变化条件下有效跟踪最大功率点,但是需要检测外界光照强度和光伏电池的短路电流,并进行大量的数据预处理来确定算法的关键参数,因此实际实现比较困难,实用性不高.

图1 变步长算法示意图Fig.1 Diagram of variable step-size algorithm
2 自适应变步长电阻增量法
电导增量法是基于光伏电池功率-电压输出特性曲线,通过判断功率对电压微分的符号来跟踪最大功率点,其扰动量通常选为光伏电池输出电压,因此电导增量法工作于电压控制模式.文献[12]中提出一种电阻增量法,其工作原理与电导增量法基本相同,利用光伏电池功率-电流的输出特性来实现最大功率点跟踪,将光伏电池的输出电流设定为扰动量.文献[2,5,13]指出,在光照剧烈变化条件下,基于电流控制模式的MPPT 算法比电压控制模式的MPPT 算法有更高的灵敏度.因此,为解决光照剧烈变化情况下光伏系统的最大功率跟踪问题,文中在电阻增量法的基础上提出一种自适应变步长电阻增量法.
2.1 步长转换函数
结合光伏电池的输出特性,步长转换函数F 取为功率对电流微分的绝对值与电流的乘积:

图2 为标准化的功率P、|dP/dI|和步长转换函数F 与电流I 的关系图.
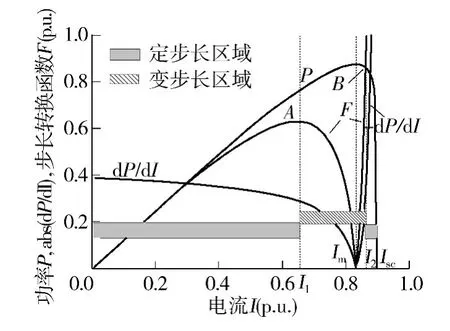
图2 标准化功率和电流步长切换函数Fig.2 Normalized power and thrshold function versus curr ent
从图中可以看出,步长转换函数F 在最大功率点(MPP)处值为0,在靠近最大功率点的左侧有一个极值点A(对应电流I1),在最大功率点右侧与功率曲线P 有一个交点B(对应电流I2).根据步长转换函数的这一特征,光伏系统的工作模式可以设定为:当光伏电池的输出电流在I1与I2之间时,系统工作在变步长模式.反之,系统工作在定步长模式.
步长工作模式之间的切换可通过下式实现:

式中,dF/dI 是步长转换函数对输出电流的微分,Im为最大功率点电流. 当外界环境条件改变使得光伏电池输出特性发生变化时,步长转换函数将重新对定步长区域和变步长区域进行划分,可以有效避免文献[6,10]中所提算法将定步长区域和变步长区域固定不变所引起的“死区”,从而使光伏系统即使在光照剧烈变化条件下也能保持良好的最大功率点的跟踪性能.
2.2 初始定步长整定
比较光伏电池在不同环境下的输出P-I 特性曲线,不难发现:在最大功率点左侧区域,P-I 曲线较为平坦;而在右侧区域,P-I 曲线较为陡峭.即在相同扰动步长的作用下,最大功率点两侧的功率变化差别较大.因此,最大功率点两侧选用符合此特性的扰动步长有助于进一步提升动态响应速度和稳态精度.
分别作用于最大功率点左侧和右侧的初始定步长ΔIref1和ΔIref2之间的关系满足下式:

式中,Im和Isc分别表示给定条件下光伏电池最大功率点电流和短路电流.由短路电流系数法可知,光伏电池最大功率点电流和短路电流近似满足以下线性关系:

式中,k 为短路电流系数.因此

由于在任意光照强度和温度下,短路电流系数k 为常量,其值介于0.78 ~0.92 之间,因此初始定步长ΔIref1与ΔIref2的比值在外界环境条件变化时也是恒定不变的.
2.3 速度因子及其收敛性
选定初始定步长ΔIref1和ΔIref2作为变步长区域的步长上限,结合步长转换函数与输出功率的关系,步长更新规则可以定义为

式中,N(k)为修正步长的速度因子,

ΔIref为扰动步长,ΔIref1、ΔIref2需满足式(7).

下面分析速度因子N(k)工作在变步长区域时的收敛性:
(1)系统工作在最大功率点处时,有dP/dI=0,步长转换函数F(k)=I(k)|dP/dI| =0,则速度因子N(k)=0.即最大功率点处,步长变化量为0.


(2)系统工作在最大功率点左侧变步长区域时,速度因子为:ΔU(k)/ΔI(k)<0,则N(k)<1;所以0 <N(k)<1.
(3)系统工作在最大功率点右侧变步长区域时,步长转换函数F(k)单调递增,0 <F(k)<PI=I2,光伏电池输出功率P(k)单调递减且PI=I2<P(k)<Pm(PI=I2表示当电流I 为I2时的功率),因此,对速度因子N(k)=F(k)/P(k),有N(k)单调递增,且0 <N(k)<1.
5.中国特色反腐倡廉道路。党的十六大以来,以胡锦涛为总书记的党中央,坚持标本兼治、综合治理、惩防并举、注重预防的方针,扎实推进惩治和预防腐败体系建设,在坚决惩治腐败的同时,更加注重治本,更加注重预防,更加注重制度建设,拓展从源头上防治腐败工作领域,走出了一条适合中国国情的、具有中国特色的反腐倡廉道路。党的十八大报告进一步明确了中国特色反腐倡廉道路的基本点,即:坚持中国特色反腐倡廉道路,方针是标本兼治、综合治理、惩防并举、注重预防,重点是全面推进惩治和预防腐败体系建设,目标是干部清正、政府清廉、政治清明,从而为反对腐败、建设廉洁政治指明了方向。
图3 所示为速度因子N(k)的变化曲线,从图中可以看出,在变步长区域,速度因子的变化趋势符合上文收敛性的分析,验证了该算法的收敛性.自适应变步长电阻增量法在远离最大功率点的工作区域采用较大步长的定步长算法;在靠近最大功率点的工作区域采取变步长算法,且步长具有越靠近最大功率点越小的特性;在最大功率点处,步长为0.

图3 速度因子N(k)、功率P 的变化曲线Fig.3 Slopes of proportionality factor N(k)and power P
3 仿真
在Matlab/Simulink 搭建光伏系统仿真模型,光伏电池和Boost 变换器参数[18]如表1 所示.
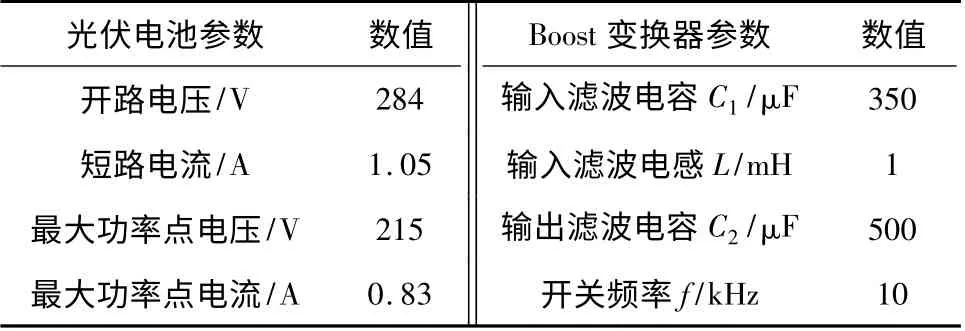
表1 仿真与实验参数Table1 Experimental parameters
设定光照强度在0.1 s 时刻从300 W/m2上升到1000 W/m2,在0.2 s 时又降低到300 W/m2.在相同的仿真条件下分别验证定步长电阻增量法、变步长电阻增量法和改进型变步长电阻增量法的最大功率点跟踪性能,图4 为各个控制算法的输出最大功率波形图,具体仿真结果对比如表2 所示.

图4 控制算法仿真波形Fig.4 Simulation waveforms of control algorithm
图4(a)、4(b)所示为定步长电阻增量法扰动步长分别为0.01和0.04 A 时的仿真结果,从表2 所提供的仿真结果对比来看,扰动步长为0.04 A 的光伏系统在光照突变时的响应时间要明显短于扰动步长为0.01 A 时,但是其在1000 W/m2时的稳态跟踪精度要比扰动步长为0.01 A 时低3.7%.这表明:选取较大的步长可提高系统在外界环境变化时的动态响应速度,但相应的系统稳态功率损失也增多.较小的步长有助于取得较高的稳态精度,但会减慢跟踪速度.

表2 MPPT 仿真结果Table 2 Simulation results of maximum power point tracking
图4(d)、4(e)所示为自适应变步长电阻增量法的输出波形,图4(d)采用的是相同大小的扰动步长,图4(e)则采用满足式(7)比例关系的扰动步长.从表2 中提供的仿真结果对比可以看出,相比于扰动步长为0.01 A 的定步长电阻增量法,自适应变步长算法可以大约降低73%的响应时间,同时相比于扰动步长为0.04 A 的定步长电阻增量法,稳态跟踪精度提高了4%.这表明自适应变步长电阻增量法可解决定步长算法因扰动步长的选取导致的稳态精度和跟踪速度之间的矛盾.对比图4(d)和图4(e)的仿真结果,可以看出在最大功率点两侧选用不同的扰动步长可避免工作点超调,从而进一步提高系统响应速度.
4 实验
为验证所提控制策略的有效性,搭建如图5 所示的实验测试平台,该平台包括一台Chroma 光伏电池阵列模拟器6200 H,用于模拟不同光照强度和温度条件下光伏电池的输出特性;一台基于DSP(TMS320F28035)控制的5 kW 双级式光伏并网逆变器,以及一台Agilent 示波器DSO7014B.实验采用的光伏电池和Boost 变换器参数与仿真参数保持一致.

图5 实验测试平台Fig.5 Experimental test setup
通过光伏阵列模拟器设定串并联的光伏电池数目,可模拟外界光照强度或温度变化.将光伏阵列模拟器的输出功率从1427W 升高到3035W 来模拟光照强度突然增加的情形. 图6 所示为各个算法的实验波形,从图6 中可以看出:在光照强度增加的情况下,采用0.01 A 定步长电阻增量法达到稳态的时间是5.072 s;采用0.04 A 定步长电阻增量法达到稳态的时间是0.578 s;采用变步长电阻增量法达到稳态的时间是3.92 s;采用ΔIref1=ΔIref2=0.04 A 自适应变步长电阻增量法达到稳定的时间是0.79 s;采用ΔIref1=0.04 A,ΔIref2=0.01 A 自适应变步长电阻增量法达到稳定的时间是0.758 s.
再将光伏阵列模拟器的输出功率从1 427 W 降低到713 W 来模拟光照强度突然降低的情形. 图7所示为各个算法的实验波形,从图中可以看出:在光照强度降低的情况下,采用0.01 A 定步长电阻增量法达到稳态的时间是1.0 s;采用0.04 A 定步长电阻增量法达到稳态的时间是0.50 s;采用变步长电阻增量法达到稳态的时间是0.70s;采用ΔIref1=ΔIref2=0.04 A 自适应变步长电阻增量法达到稳定的时间是0.644 s,采用ΔIref1=0.04 A、ΔIref2=0.01 A 自适应变步长电阻增量法达到稳定的时间是0.394 s.

图6 光照强度增加实验波形Fig.6 Experiment waveforms when light intensity increases
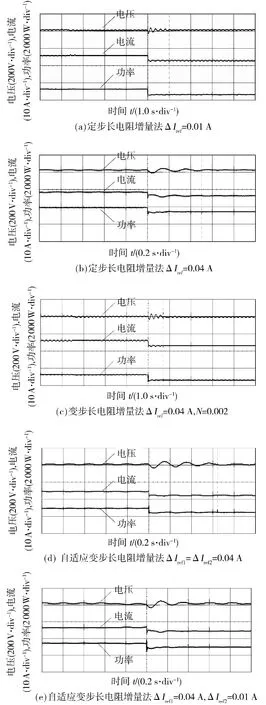
图7 光照强度减小实验波形Fig.7 Experiment waveforms of when light intensity decreases
以上实验数据表明,在光照强度剧烈变换的情况下,自适应变步长电阻增量法可有效提高系统的动态响应速度,同时,从稳态输出波形来看,自适应变步长算法也表现出较高的跟踪性能.
以上实验测试的是光照强度剧烈变换情况下最大功率跟踪算法的控制性能,而在实际应用中,光照强度一般为连续缓慢变化的情形. 通过光伏阵列模拟器设定输出功率为:534 W-2136W-1958W-1602W-1168W-534W,图8 为模拟光照强度连续变化时自适应变步长电阻增量法的实验波形,从实验结果来看,自适应变步长电阻增量法无论在外界光照上升还是下降的情况下都能够快速稳定地跟踪最大功率点,因此该方法同样适用于实际光伏系统.

图8 光照连续变化实验波形Fig.8 Experiment waveforms when light intensity continuously changes
5 结论
为解决外界环境剧烈变化条件下光伏系统最大功率跟踪问题,提出一种自适应变步长电阻增量法,并搭建Matlab/Simulink 仿真模型和基于 DSP(TMS320F28035)控制的5 kW 光伏系统实验平台,将文中提出算法与定步长算法和传统变步长算法进行对比实验,得到以下结论:
(1)自适应变步长算法解决了定步长算法中响应速度、稳态精度和扰动步长选取之间的矛盾,以及传统变步长算法在光照剧烈变化条件下的跟踪时间较慢的问题.
(2)在外界环境(光照)剧烈变换的条件下,自适应变步长电阻增量法相比于定步长电阻增量法和传统变步长算法,可以将系统的响应速度提高73%,同时可使稳态跟踪精度达到98.9%.
(3)模拟自然条件下外界环境(光照)缓慢变换情形,自适应变步长算法依然具有较好的动态和稳态性能.
此外,所提算法具有相对简洁的控制逻辑和较小的计算量,可较为方便地利用DSP 实现,在光伏发电系统中有较好的应用前景.
[1]赵争鸣,陈剑,孙晓瑛.太阳能光伏发电最大功率点跟踪技术[M].北京:电子工业出版社,2012.
[2]Femia N,Petrone G,Spagnuolo G,et al.Power electronics and control techniques for maximum energy harvesting in photovoltaic systems[M]. New York:CRC Press,2013:104-107.
[3]Esram T,Chapman P L.Comparison of photovoltaic Array maximum power point tracking techniques [J]. IEEE Transactions on Energy Conversion,2007,22(2):439-449.
[4]杨勇,朱彬彬,赵方平,等. 一种电流预测控制的自适应变步长最大功率跟踪方法[J].中国电机工程学报,2014,26(6):855-862.Yang Yong,Zhu Bin-bin,Zhao Fang-ping,et al.An adaptive and variable step MPPT methode based on current predictive controllers [J]. Proceedings of the CSEE,2014,26(6):855-862.
[5]Bianconi E,Calvente J,Giral R,et al.A fast current-based MPPT technique employing sliding mode control [J].IEEE Transactions on Industrial Electronics,2013,60(3):1168-1178.
[6]Montecucco A,Knox A R.Maximum power point tracking converter based on the open-circuit voltage method for thermoelectric generators[J]. IEEE Transactions on Power Electronics,2014,30(2):828-839.
[7]杭凤海,杨伟,朱文艳.光伏系统MPPT 的扰动观测法分析与改进[J].电力系统保护与控制,2014,39(9):110-114.Hang Feng-hai,Yang Wei,Zhu Wen-yan. Analysis and improvement of MPPT disturbance observer method for PV system[J]. Power System Protection and Control,2014,39(9):110-114.
[8]Abdelsalam A K,Massoud A M,Ahmed S,et al. Highperformance adaptive perturb and observe MPPT technique for photovoltaic-based microgrids[J].IEEE Transactions on Power Electronics,2011,26(4):1010-1021.
[9]刘邦银,段善旭,刘飞,等. 基于改进扰动观察法的光伏阵列最大功率点跟踪[J]. 电工技术学报,2009,24(6):91-94.Liu Bang-yin,Duan Shan-xu,Liu Fei,et al. Photovoltaic array maximum power point tracking based on improved perturbation and observation method[J]. Transactions of China Electro Technical Society,2009,24(6):91-94.
[10]唐磊,曾成碧,苗虹,等.基于切线角的光伏变步长最大功率跟踪控制策略[J]. 电力系统自动化,2013(20):28-33.Tan Lei,Zeng Cheng-bi,Miao Hong,et al.A new control strategy for MPP tracking in photovoltaic system based on contingence angle and variable step-size searching method[J].Automation of Electric Power Systems,2013(20):28-33.
[11]Liu F R,Duan S X,Liu F,et al.A variable step size INC MPPT method for PV systems[J].IEEE Transactions on Industrial Electronics,2008,55(7):2622-2628.
[12]Mei Q,Shan M,Liu L,et al. A novel improved variable step-size incremental-resistance MPPT method for PV systems[J]. IEEE Transactions on Industrial Electronics,2011,58(6):2427-2434.
[13]Kollimalla S K,Mishra M K.A novel Adaptive P&O MPPT algorithm considering sudden changes in the irradiance[J]. IEEE Transactions on Energy Conversion,2014,29(3):602-610.
[14]胡义华,陈昊,徐瑞东,等.一种两阶段变步长最大功率点控制策略[J].电工技术学报,2010,25(8):161-166.Hu Yi-hua,Chen Hao,Xu Rui-dong,et al. A two stagevariable step-size maximum power point tracking control[J]. Transactions of China Electrotechnical Society,2010,25(8):161-166.
[15]彭会锋,孙建平,曹相春,等.基于功率占空比微分曲线的光伏系统MPPT 算法[J]. 电力自动化设备,2013(6):124-127.Peng Hui-feng,Sun Jian-ping,Cao Xiang-chun,et al.MPPT algorithm based on power duty cycle differential characteristic curve for photovoltaic system[J].Electric Power Automation Equipment,2013(6):124-127.
[16]Chen Y,Lai Z,Liang R.A novel auto-scaling variable stepsize MPPT method for a PV system [J]. Solar Energy,2014,102:247-256.
[17]Piegari L,Rizzo R. Adaptive perturb and observe algorithm for photovoltaic maximum power point tracking[J]. IET Renewable Power Generation,2010,4(4):317-328.
[18]Erickson R W,Maksimovic D. Fundamentals of Power Electronics[M].Berlin:Springer,2001.

