随机路网中风险爱好出行者的路径选择分析*
俞礼军 杨灿杰
(华南理工大学 土木与交通学院,广东 广州510640)
交通拥堵是快速发展的大城市交通亟待解决的问题,交通分配是设计交通拥堵问题解决方案的理论基础.从对路段行程时间的特性,以及驾驶人对路段行程时间的认知这两个方面的假设出发,可将交通分配模型分为4 种类型:其中确定性路网的确定性用户均衡[1](DN-DUE)与确定性路网的随机用户均衡(DN-SUE)模型相对比较简单,在30年前已经有比较成熟的研究成果[2]. 随机路网的确定性用户均衡(SN-DUE)与随机路网的随机用户均衡(SNSUE)模型与算法研究则较滞后. 一般认为,随机路网条件下的交通分配更加接近实际路网的特征,因而对于交通网络设计与交通拥堵解决具有重要的应用价值和理论价值. 文中期望基于新近发展起来的新随机用户均衡模型以等价负效用最小化为路径选择准则反映驾车出行者的路径选择行为,尝试研究风险倾向出行者与路段交通拥堵的关系.
自20 世纪80年代以来,国外学者就已经对随机路网的均衡分配问题进行了理论研究. Soroush[3]首次基于负效用函数给出一个简单的SN-DUE 模型对应的非线性互补问题解析表达式. Mirchandani等[4]采用风险倾向来描述出行时间与出行时间变异性对于出行者在路径选择决策中的作用,并首次将路网的不确定性与出行者的感知误差引入路径选择模型,得到了SN-SUE 模型. Tatineni 等[5]定义风险为出行时间的随机性,根据出行者风险倾向将出行者分为3 类:风险规避、风险爱好、风险中立.风险一词在这里指的是推迟到达目的地的成本或代价的不确定性.对于风险爱好型驾车出行者,他(她)会选择行程时间短,但行程时间变异性大的路径.风险中立型驾驶人则不会把行程时间变异性考虑到他/她的路径选择决策中去. Tatineni 等研究发现,相同路网与特定起迄点之下,确定型与随机型两类模型分配得到的路段交通量上的差异对于远期交通规划预测没有明显差别,但两种模型分配的交通量对于短期交通流管理,尤其是对于使用导航系统出行交通流的预测差别十分显著.Chen 等[1]延续之前学者的研究,认为驾车出行者在做路径选择决策时,出行时间的变异性(不确定性)是一种风险(出行成本),部分出行者愿意为了规避风险而付出额外成本. 大量关于SN-DUE 与SN-SUE 的研究有一个共同的特点:均假定路段行程时间(或其通行能力)服从某种随机分布形态. 这样的SN 交通分配模型的计算十分复杂,难以被广大从业人员理解、应用.Cheu 等[6]针对上述缺陷,在对路段行程时间的随机分布形态不做任何假设的条件下,导出一个简单的等价路段负效用(Simpler ELD)函数,加入该函数后的SNDUE 模型可以转化为DN-DUE 模型,从而用传统的用户均衡求解方法实现交通分配,这是一个新的思路.上述代表性学者在SN-DUE 与SN-SUE 方面做了开拓性研究.
Cheu 等[6]提出的方法实现了用传统的用户均衡求解方法处理SN-DUE 的交通分配. 笔者将文献[6]思路推广到更为一般的SN-SUE 情况,即基于具有一般代表性的Weibull 型随机用户均衡模型开展随机路网中有风险倾向的驾车出行者的路径选择与交通分配研究,并分析风险倾向与路段交通拥挤现象之间的关系.
有必要指出的是,虽然Castillo 等[8]提出并研究了Weibull 型随机用户均衡模型,但并未探讨交通分配实现的算法,文中就此提出了效用最小化作为路径选择准则的SN-Weibull SUE 模型中的实现算法.此外,还首次研究了典型SN-SUE 模型框架下风险系数等参数与路段流量之间的敏感性. 还需要说明的是,目前国际上实证、一般理论研究中多假定出行者的出行风险倾向属于风险中立或规避型[1、6-7],这种假设和笔者在部分城市调查的实际情况不符.笔者调查发现,整体驾车者属于风险爱好倾向(此结果可能与我国的惩罚制度有关). 因此文中的算例研究中采用风险爱好型的风险系数,从计算结果可以发现,驾车者整体的风险爱好倾向能够部分解释一些路段的拥挤加剧现象,由此可从机理上得到我国城市交通拥挤加剧现象的一个新的解释.
1 模型
考虑网络G=(N,A),其中N 是节点集,A 是有向路段集.令a 为一路段,a∈A.对整个交通网络做以下假设:(1)网络是强连通的;(2)路段阻抗函数是关于路段流量的连续可微的严格增函数并且只取正值.
1.1 路段阻抗与负效用函数
DN-DUE 与DN-SUE 根据路段阻抗函数求解;SN-DUE 与SN-SUE 基于路段负效用函数求解[1].
1)路段阻抗函数
路段出行时间采用美国公路局开发的路段阻抗公式BPR 路阻函数,其形式为
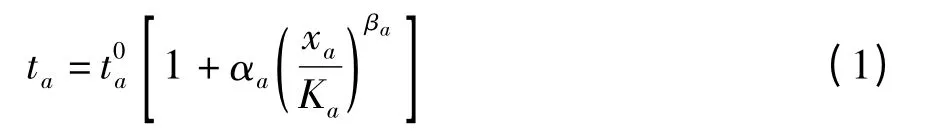
2)路段负效用函数
文献[1、3-4]中惯用的描述随机路网中风险偏好驾车出行者的路段负效用函数为
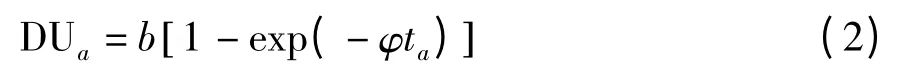
式中,DUa为路段a 的负效用,b、φ 均为正的常数,ta为路段行程时间.
针对式(2)可得简化的等价路段负效用函数为[6]:

由文献[6]知,φ >1 表示风险规避型出行者,φ=1 表示风险中立型出行者,φ <1 表示风险爱好型出行者. 式(3)类似于BPR 函数,对于使用BPR 形式阻抗函数随机路网的交通分配问题,它不仅免除了对路段行程时间概率分布假设,还简化了计算的复杂度.
1.2 随机路网Weibull-SUE 模型
设某OD 点对w,w∈W 之间每个出行者选择他期望路径负效用最小的路径为路径k 的实际时间(阻抗),εk为随机变量. 在通常使用的BPR 路段阻抗函数中用φα 的值直接替换BPR 函数中的参数α 得到BPR 形式的等价路段负效用函数,令为路径k 与l 的路径负效用,路径k 的选择概率为,k∈Rw.其中,Pr(·)表示求概率. 假定服从独立Weibull 分布[8],即,其中ξw为位置参数,为尺度参数,ηw为形状参数,可得随机路网中路径选择概率公式:

从形式上看,随机路网Logit 选择概率模型是式(4)的特例,因而随机路网Weibull 型随机用户均衡模型更具有一般性.
设OD 点对w,w ∈W 之间的交通需求为qw,基于Weibull-SUE 模型得到的路段流量为xa=式中为0 -1 变量,若OD 对间的路段a 在路径k 上,则取1;反之,取0.若可得则Weibull-SUE 模型存在且有唯一的不动点[9].由文献[8]知,在上述条件下Logit-SUE 与Weibull-SUE 是等价的. 应用DN-SUE 算法,即完成SN-SUE 模型的求解.
2 随机路网交通分配算法与敏感性分析
2.1 随机路网Weibull-SUE 交通量分配算法
只要算法设计得当,则随机路网Weibull-SUE模型解存在、唯一的结论保证能够找到原问题的解.文中提出如下组合迭代算法求解随机路网Weibull-SUE 模型.具体算法步骤为:
步骤1 初始化.给定每一OD 对w 的出行需求量qw、每一路段的BPR 形式负效用函数及对应的参数αa(αa=φαa随机路网考虑风险)、βa和;给定关联矩阵(若OD 对w 的路径k 包含路段a,则=1,否则为0);给定松弛系数ρ(可取0.2),0 <ρ <1(其取值类似于线性方程组的低松弛迭代)、容许误差ε、最大迭代次数itermax.确定每一OD 对w 对应的Weibull 分布的位置参数以及形状参数[10]ηw,给定每一个路段初始交通量xa,令iter=0.
步骤2 负效用函数的计算.基于xa计算路段负效用ta,置迭代次数iter=iter+1,令
步骤3 路径选择概率的计算.由路段阻抗ta及关 联 矩 阵, 根 据 求 得 的 路 径 负 效 用基于,由得到对应于每条路径的尺度参数的估计值,由算得OD对w 间路径k 的选择概率.
步骤6 路段交通量组合松弛迭代计算.根据已有的交通量xa和步骤4 分配的交通量x′a,对路段交通量进行更新:xa=(1-ρ)xa+ρx′a(a∈A).转步骤2.
步骤7 结果输出.如果≤ε,iter≤itermax,输出路段交通量xa和路径阻抗及其选择概率;否则,停止运算,输出迭代itermax次后未收敛的警告.
文中模型及算法适用于一般网络.
2.2 参数的敏感性分析
根据前述分配算法,联立BPR 形式的负效用函数、路径选择概率算式、路段交通量计算式,可得计算路段交通量的一般表达式为
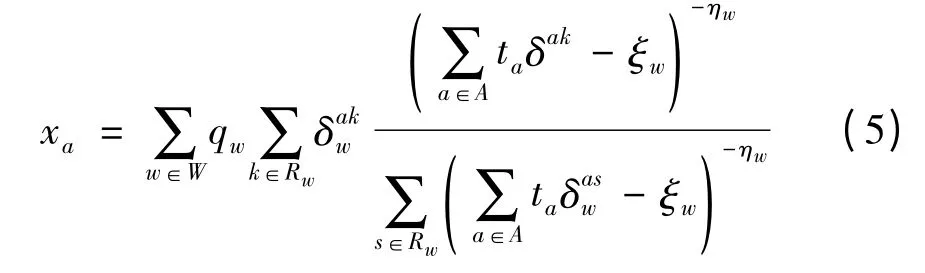
由式(13)可以直接得敏感性分析表达式[11].令表示g(·)中除去xa、之外的变量与参数.由xa=g(xa,,ψ)可得路段流量对于参数的敏感性分析算式进一步处理可得在通常情况下,计算、使用无量纲的相对比值将其用于相对敏感度分析并做横向比较更为便利.
3 算例
采用Maher 等[12]所用的路网作为测试路网,具体如图1 所示.该路网一共有9个节点和24个单向路段,路网中共有4个出行OD 对,起-讫点分别是1 -5、5 -1、3 -7、7 -3. 数值模拟中使用BPR 形式路段费用函数,αa=1,βa=4,a∈A.每个路段自由流条件下的时间(阻抗)、通行能力与风险倾向的系数φαa如表1 所示,其中,风险系数由调查得到,φ =0.5476.出行需求量、出行路径如表2 所示.

图1 测试路网Fig.1 An example network
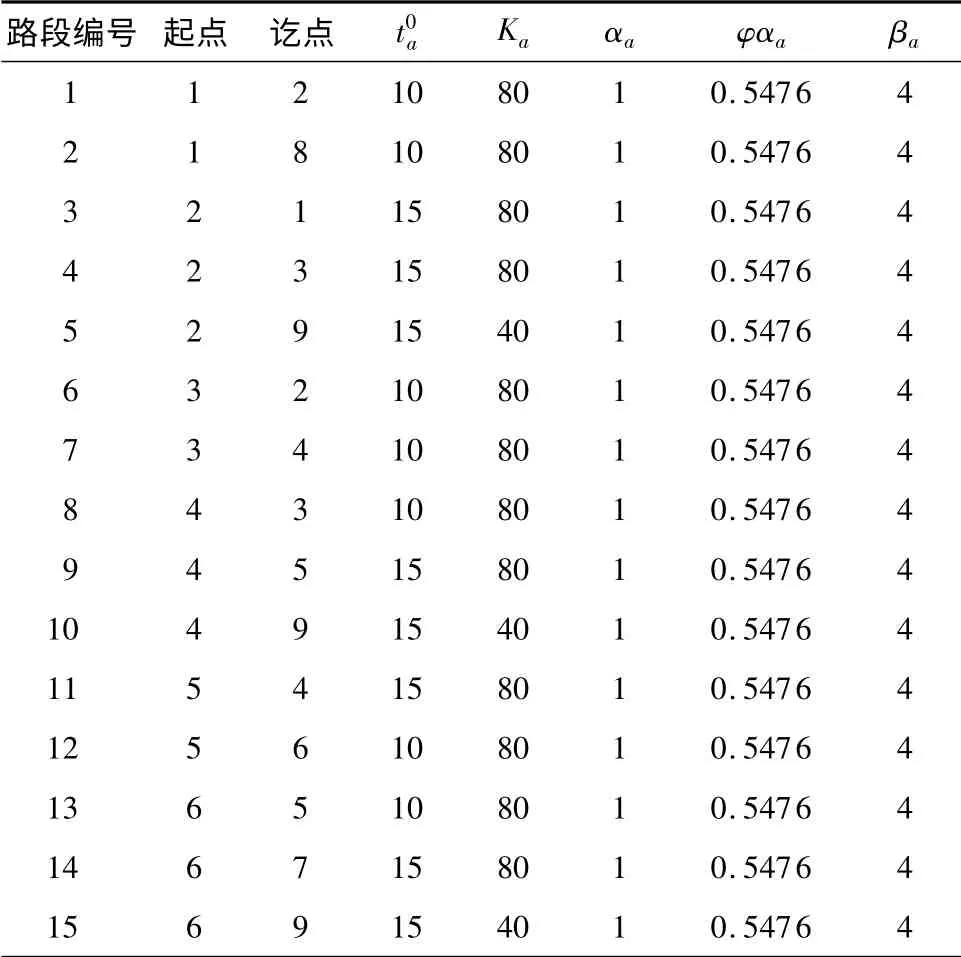
表1 路网特性参数Table 1 Parameters of the example network
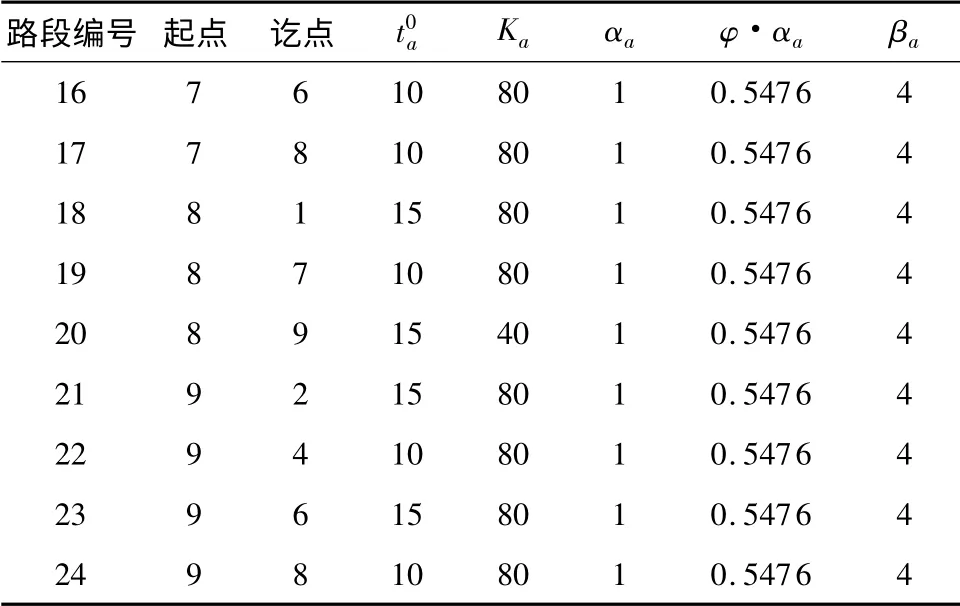
续表1
表1 风险系数φ 获得方法如下[6]:假设在一个OD 对之间只连接着两条平行的路段1 与2,假定路段1 的行程时间为常数t1,路段2 行程时间的最小值和平均值分别为和.在人为给定值和值之后,让驾车出行者指定一个使其对两条路段具有相同负效用的t1值,把调查数据代入式(3)可以得到每一个出行者的φ 值.
Logit-SUE 模型参数θw均取0. 195,Weibull-SUE 模型参数ηw分别取3.5、2.45、1.75、2.45,ξw分别取40、45、50、45,w 为表2 的OD 对.θw、ηw的取值是为了使得确定型路网中Weibull-SUE 模型和经典的Logit-SUE 有基本相似的分配结果. 根据前述算法,基于不考虑风险的BPR 函数和考虑风险的路段负效用函数分别应用独立Gumbel 分布和独立Weibull 分布SUE 模型编程求解得到的路段交通量结果如表3 所示.
路段交通量xa关于参数的敏感度计算结果如表4 所示. 由于它们的数目比较多,从中选取一部分来进行说明,表4 中第1 列为需要计算敏感度的参数,以后各列为对应路段的敏感度的绝对值,敏感度的相对值使用括弧表明,并写在相应值的正下方.敏感度值越大,其对路段交通量的影响也就越大. 以下参数αa的数值等于φαa,后面针对φ 的敏感性分析均用αa表示.
1)路段19 与路段8、15 不同在一个路径上,无相互作用,因而路段8、15 交通量对路段19 的参数α19的敏感度值为0.路段19 的参数α19增加则其交通量减少,故路段19 交通量对其风险阻抗参数α19的敏感度值小于0. 路段5、20 与路段19 有竞争关系,路段19 参数α19增加,则路段5、20 流量增加,对应的敏感度值大于0. 路段19 与路段2、16 在同一路径上,若路段19 参数α19增加,则路段2、19、16 的
流量均减少,即相应的敏感度小于0. 另外,对于冒险性的驾驶者而言,若假定其他因素不变化,则意味着α19(因风险系数小于1)减少,故对应的路段5、20交通量减少.

表2 出行路径与OD 需求量Table 2 Flows of OD-pairs and paths in the example network
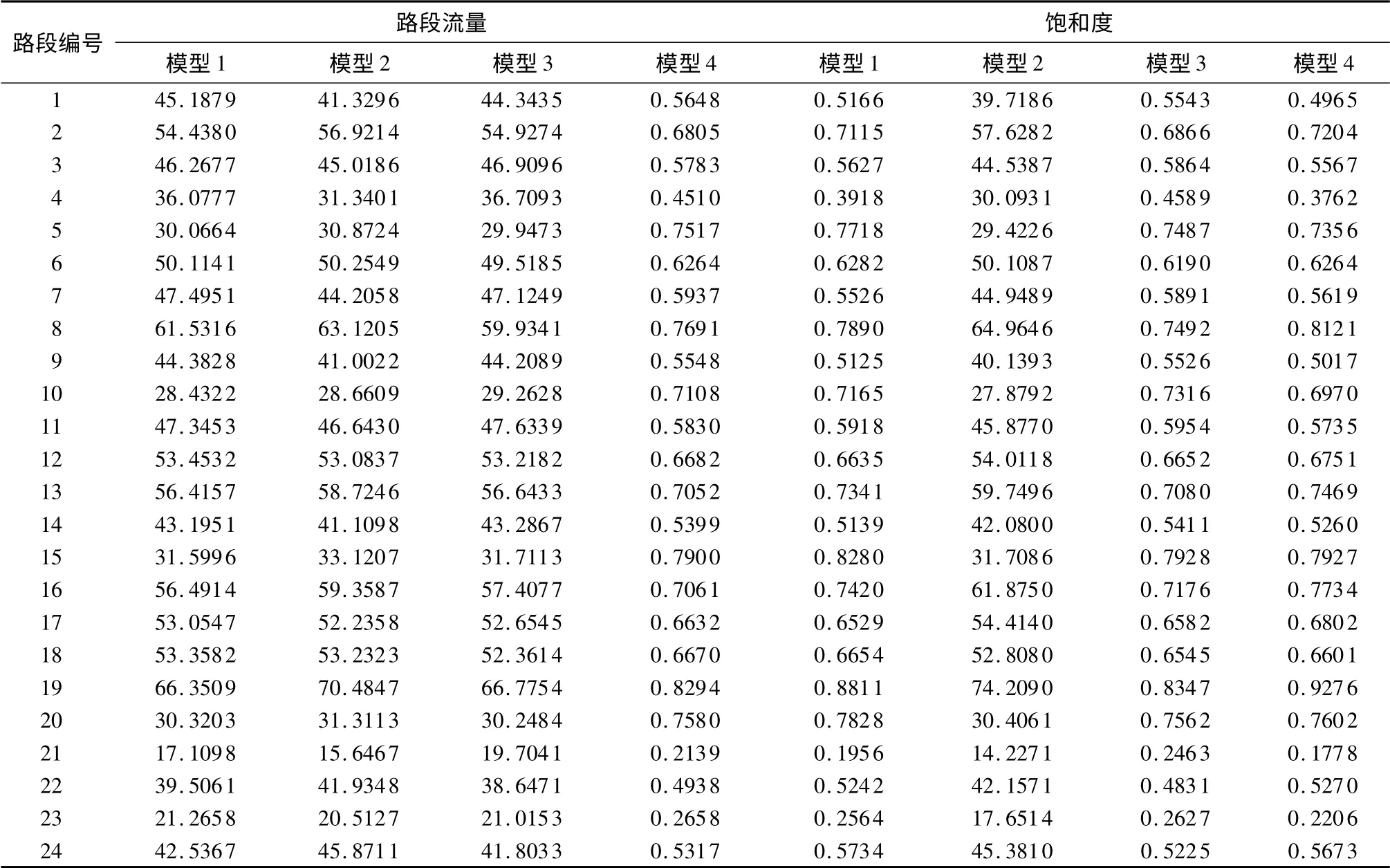
表3 SUE 模型路段交通量的比较1)Table 3 Comparison of link flows resulting from different SUE models
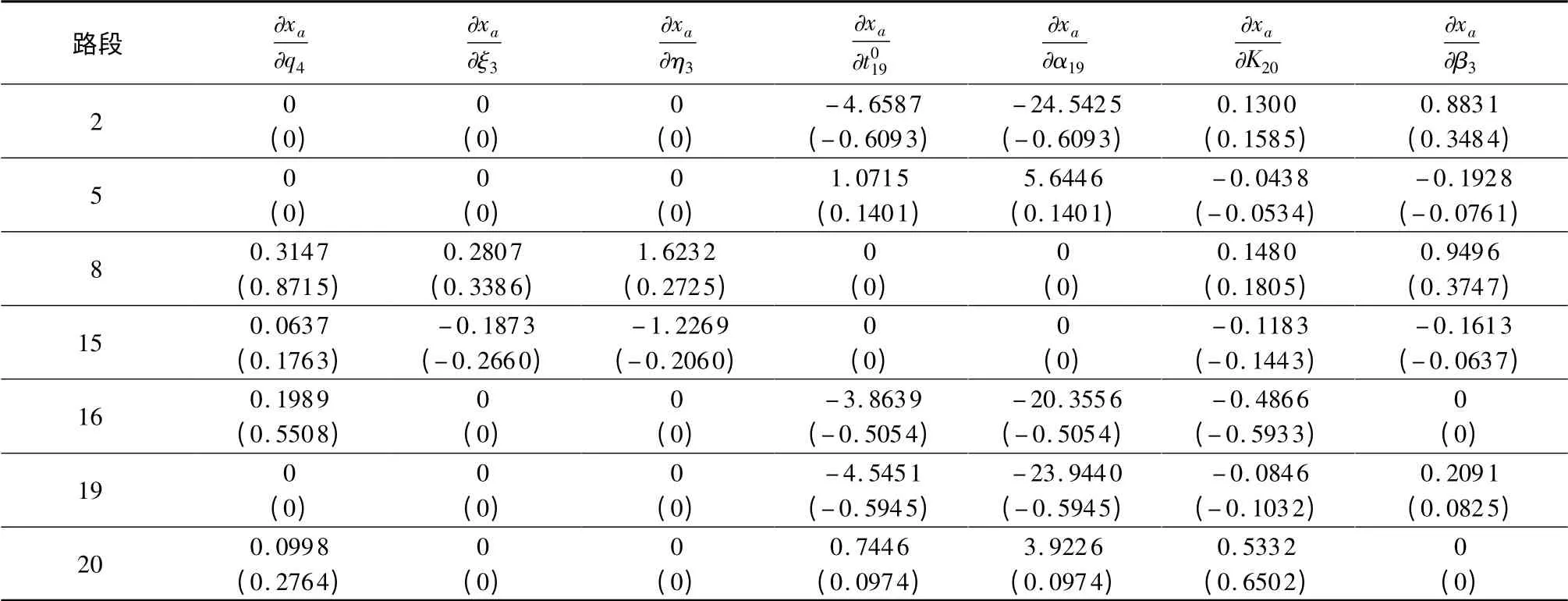
表4 敏感度分析表Table 4 Sensitivities analysis table
2)表中数据较多,仅以位置参数ξ3为例说明.ξ3是第3个OD 对间所有路径自由流条件下的最小阻抗.路段2、5、16、19、20 由于不包含在第3个OD对间的任一路径上,故其交通量的敏感度为0;而由于路段8、15 包含在其路径上,故其对应的交通量敏感度值不为0. 类似的可以就特定路段交通量关于相应参数的敏感性展开分析,此处不再赘述.
4 结论
结合风险偏好型出行者的等价路段负效用函数与Weibull 随机用户均衡构建随机路网Weibull 随机用户均衡模型,文中将SN-DUE 推广到更为一般的SN-SUE 情况并设计了对应模型的求解算法,基于测试算例,得到如下研究结论:
1)若组合系数选择合适,组合迭代算法能够有效用于SN-Weibull SUE 模型且计算效果理想;
2)路段交通量对风险系数的敏感度分析表明,风险系数对于部分路段的交通量有显著的影响. 风险偏好驾车出行者会加剧某些路段的交通拥堵,基于随机路网中风险爱好出行者的交通分配能够解释部分路段交通拥挤加剧的现象;
3)基于算例可知,确定型路网与随机路网条件下Logit-SUE 模型、Weibull-SUE 模型针对风险中立,风险爱好出行者的交通分配结果有差异,随机路网中风险爱好倾向的驾车出行者使得路网总的行走时间增加.一定条件下的Logit-SUE 模型、Weibull-SUE模型的分配结果差异不显著,这和文献[8]结论一致;
4)将风险偏好融合到BPR 形式负效用函数中,免除了对路段行程时间概率分布的假设,还简化了计算的复杂度,可以帮助运输系统建模者实现随机路网中对应的随机均衡交通分配,协助分析交通规划、管理问题.
[1]Chen A,Ji Z W,Recker W. Travel time reliability with risk-sensitive travelers[J]. Transportation Research Record,2002,1783:27-33.
[2]Sheffi Y. Urban transportation networks:equilibrium ana lysis with mathematical programming methods[M]. NJ:Prentice Hall England Cliffs,1985.
[3]Soroush H.Routes and flows through stochastic networks.[D]. Troy,New York:Rensselaer Polytechnic Institute,1984.
[4]Mirchandani P,Soroush H.Generalized traffic equilibrium with probabilistic travel times and perceptions [J].Transportation Science,1987,21(3):133-152.
[5]Tatineni M,Boyce D,Mirchandani P.Experiments to compare deterministic and stochastic network traffic loading models [J]. Transportation Research Record,1997,1607:16-23.
[6]Cheu R L,Kreinovich V,Manduva S R.Traffic assignment for risk-averse drivers in a stochastic network[C]∥Proceedings of the 87th Annual Meeting of the Transportation Research Board.Washington D C:[s.n.],2008.
[7]Fernando O,Nicolás E S.Wardrop equilibria with risk-averse users[J].Transportation Science,2010,44(1):63-86.
[8]Castillo E,Menéndez J M,Jiménez P,et al. Closed form expressions for choice probabilities in the Weibull case[J]. Transportation Research,Part B:Methodological,2008,42(4):373-380.
[9]Patriksson M,Labbé′s M.Transportation planning:state of the art[M].NY:Kluwer Academic Publichers,2002:53-68.
[10]方开泰,许建伦.统计分布[M]. 北京:科学出版社,1987:231-235.
[11]Fiacco A V. Introduction to sensitivity and stability ana lysis in nonlinear programming [M]. NY:Academic Press,1983.
[12]Maher M J,Zhang X Y,Vliet V D. A bi-level programming approach for trip matrix estimation and traffic control problems with stochastic user equilibriumlink flows[J]. Transportation Research,Part B:Methodological,2001,35(10):23-40.
[13]俞礼军,王蕾云.MNP 模型参数估计实用方法及其在出行方式预测中的应用[J].华南理工大学学报:自然科学版,2014,42(2):103-108.Yu Li-jun,Wang Lei-yun.Practical method of MNP model prameter estimation and its application to forecast of trip mode choice[J].Journal of South China University of Technology:Natural Science Edition,2014,42(2):103-108,138.
[14]Bell M G H.Stochastic user equilibrium assignment and iterative balancing[C]∥Proceedings of the 12th International Symposium on Transportation and Traffic Theory.New York:Elsevier,1993:427-439.
[15]Damberg O,Lundgren J T,Patriksson M. An algorithm for the stochastic user equilibrium problem[J].Transportation Research Part B,1996,30(2):115-131.

