致密油藏多角度裂缝压裂水平井产能计算方法

方思冬，战剑飞，黄世军，何聪鸽

（1.中国石油大学（北京）石油工程学院，北京102249；2.中国石油大庆油田有限责任公司勘探开发研究院，黑龙江大庆163712；3.中国石油勘探开发研究院，北京100083）

致密油藏多角度裂缝压裂水平井产能计算方法

方思冬1，战剑飞2，黄世军1，何聪鸽3

（1.中国石油大学（北京）石油工程学院，北京102249；2.中国石油大庆油田有限责任公司勘探开发研究院，黑龙江大庆163712；3.中国石油勘探开发研究院，北京100083）

水平井分段压裂是致密油藏开发的关键技术。由于受复杂的地应力和天然裂缝的影响，人工裂缝通常与井筒呈一定角度，导致压裂水平井产能预测变得十分复杂。基于天然裂缝等效渗透率张量理论，建立考虑全渗透率张量的各向异性稳定渗流数学模型。在该模型的基础上，结合势叠加原理，采用考虑应力敏感的半解析方法，构建基质向人工裂缝流动的离散势函数单元。将裂缝内流体流动处理为离散单元之间的线性流动，将基质与裂缝流动耦合求解，得到考虑天然裂缝下多角度裂缝压裂水平井产能计算方法。实例计算结果表明，由于考虑了天然裂缝和人工裂缝角度的影响，计算结果与实际产量误差小于7%。敏感性分析发现，储层主渗透率方向与人工裂缝的夹角对产能影响较大。

致密油藏 全渗透率张量 压裂水平井 应力敏感 产能

致密油藏的开发主要采用水平井分段压裂技术和微地震监测技术，在部分致密油藏的开发过程中发现，裂缝发育区往往能够相对高产，成为致密油藏“甜点区”［1-4］。致密油藏压裂水平井产能评价方法为该类油藏采用压裂水平井开发的适应性筛选、布井方式优化、裂缝参数优化及合理采油参数的确定提供了科学依据。目前针对裂缝性油藏，部分学者采用连续介质渗透率张量模型［5-9］，将裂缝和基质渗透率等效为各向异性介质渗透率二阶张量，但是渗流方程中渗透率只采用渗透率张量主值，全渗透率张量很难应用在产能计算中。对于压裂水平井产能评价主要采用解析方法［10-14］，常规解析方法不能同时考虑多角度裂缝和应力敏感，对裂缝内流体流动采用径向流等效处理，计算结果一般偏大。为此，建立考虑全渗透率张量的各向异性渗流模型，利用考虑应力敏感的半解析法，构建离散势函数单元，裂缝内流体流动处理为离散单元之间的线性流动，耦合2个流动区域得到致密油藏多角度裂缝压裂水平井产能计算方法。

1　模型的建立

模型假设条件为：致密油藏多角度裂缝压裂水平井各向异性地层中存在多组天然裂缝（图1），渗透率等效为Kxx，Kxy，Kyx和Kyy共4个方向渗透率［5］，基质流动为考虑应力敏感的平面稳定渗流，裂缝内流体流动为线性流，而在井筒附近的流动为径向流，人工裂缝高度等于油层厚度。

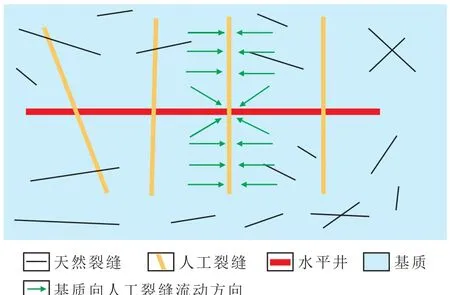
图1　致密油藏多角度裂缝压裂水平井流动示意Fig.1　Sketch of flow in the fractured horizontalwellwith multi-angle fractures in tightoil reservoir

1.1天然裂缝等效渗透率张量模型

利用平行板理论和张量理论，将裂缝性油藏简化为各向异性的等效连续介质［6］，模型中裂隙岩体的等效渗透率等于无裂隙岩石基质的渗透率与裂缝系统的渗透率的张量之和，其表达式为

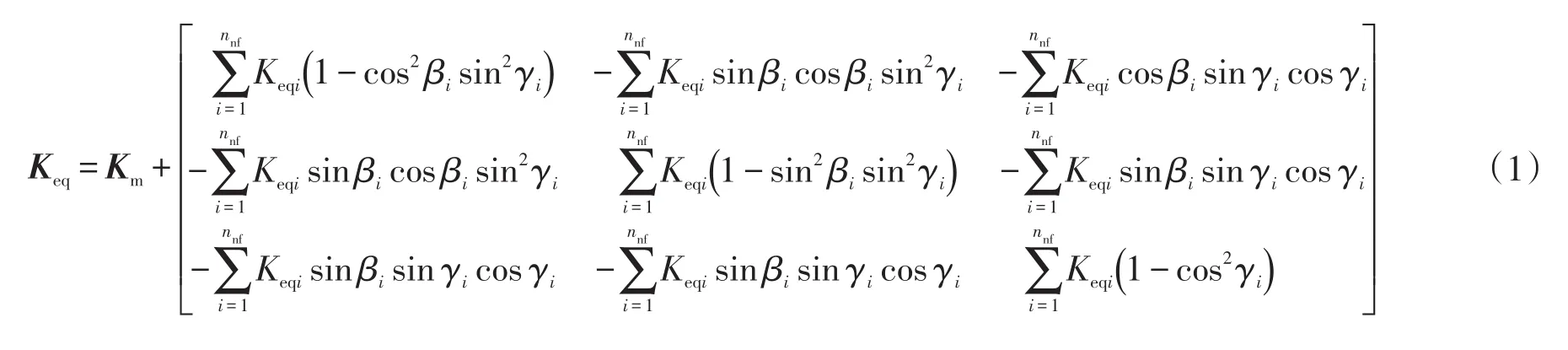
其中

对于平面渗流，式（1）可简化为

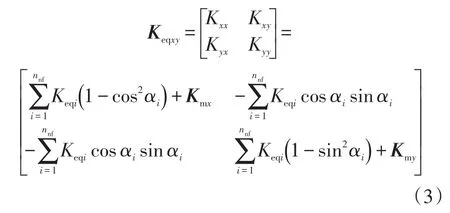
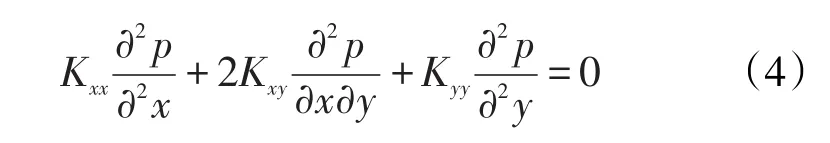
令

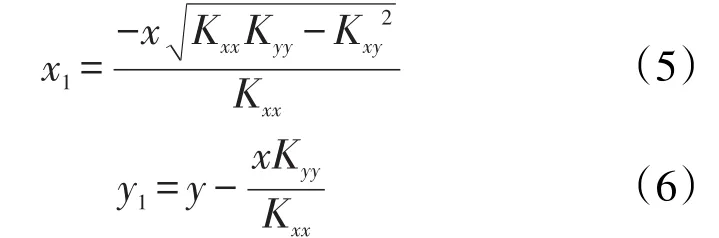
通过特征变换，将式（4）变为容易求解的拉普拉斯方程，即

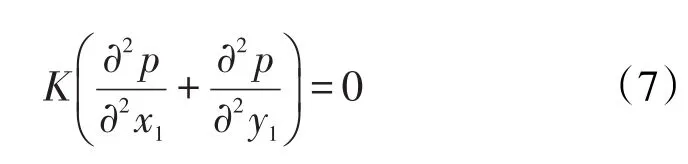
其中

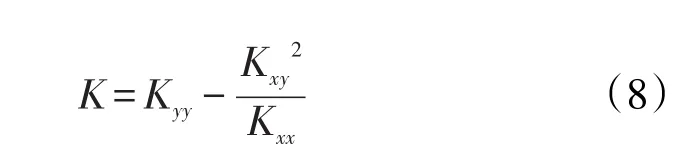
式（3）—式（8）为将天然裂缝对渗流的影响等效变换为各向同性油藏渗流数学模型。

1.2人工裂缝流动耦合计算模型

假设分段压裂水平井有N条人工裂缝，将每条裂缝离散为M个单元，整个压裂水平井分成N×M个单元。每个单元由其中心位置、单元半长和单元角度3个参数表征。

根据稳定渗流理论，考虑天然裂缝影响的压力势函数［15］表达式为

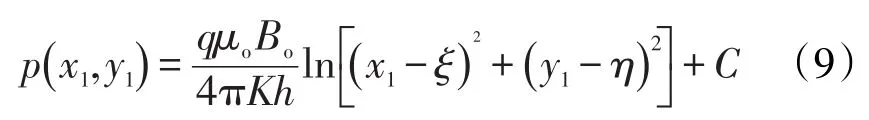
将式（9）线积分，得到离散势函数单元在平面上任意点（x，y）处产生的势表达式，即

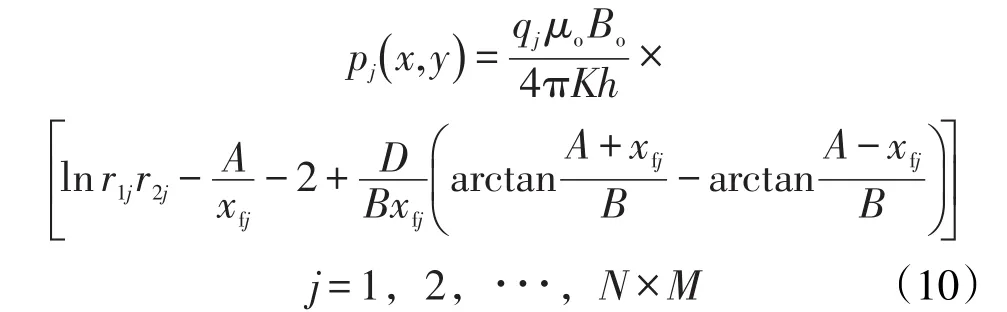
其中

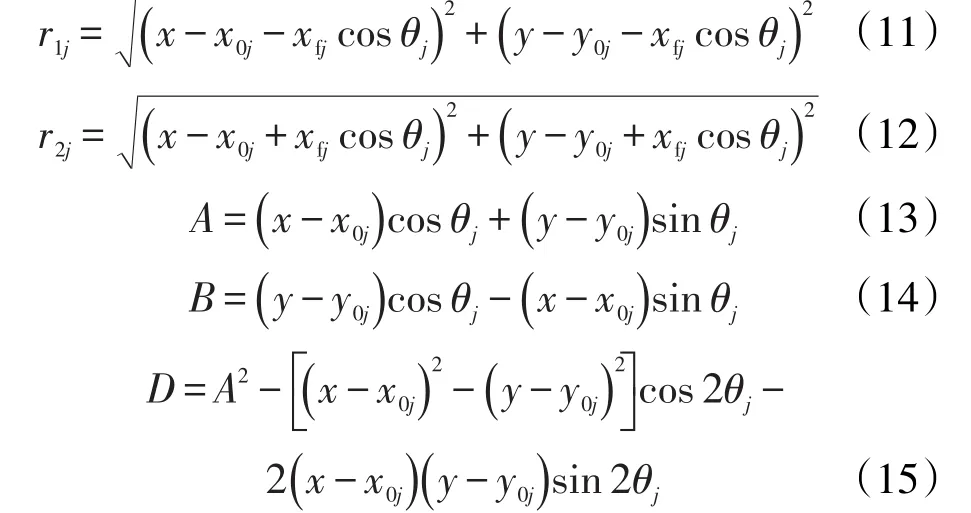
根据岩心渗透率应力敏感测试曲线回归的指数方程［15］为

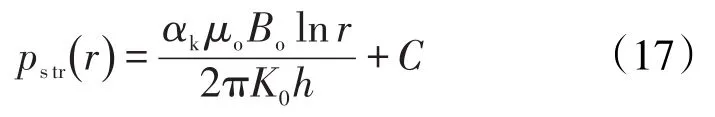
在式（10）的基础上建立考虑应力敏感势函数为

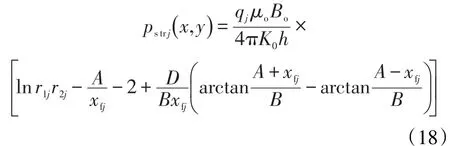
根据有限导流压裂直井的研究成果［16-17］，可将裂缝中的流体流动简化为稳定流，其中裂缝中任意点处的压力可表示为

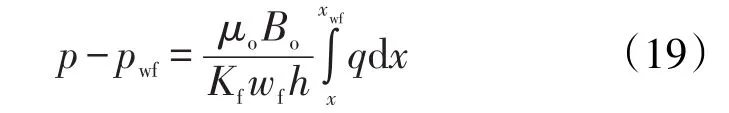
将井筒所在网格内的流体流动等效为径向流，采用Peaceman井筒流动模型［18］，其表达式为

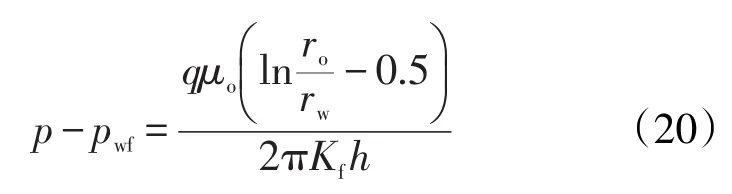
其中

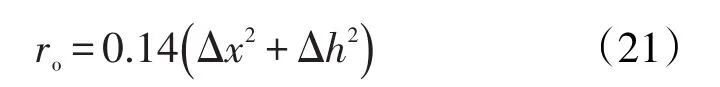
以裂缝分成关于井筒对称的5个网格为例，由左到右依次对压力和流量进行编号，非井筒所在网格中流体向井筒处流动为线性流，基于式（19）积分可得非井筒网格的压力与井筒网格的压力的关系，左端2个非井筒网格压力和井筒网格压力之差与流量的关系表达式分别为

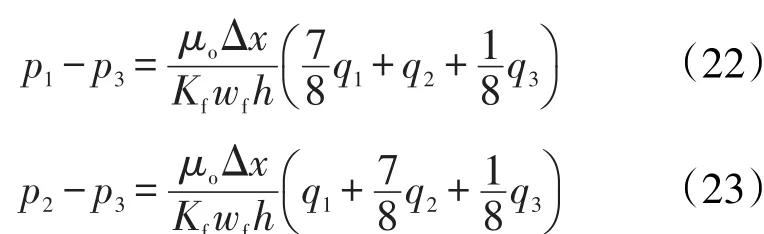
井筒所在网格中流体向井筒处流动为径向流，利用式（20）可得到井筒网格处压力与井底流压的关系，其表达式为

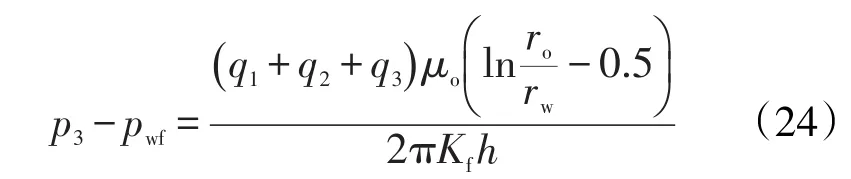
根据裂缝网格的对称性，建立的裂缝中流体流动矩阵为

因此，每个网格的压力与井底流压的矩阵关系式为

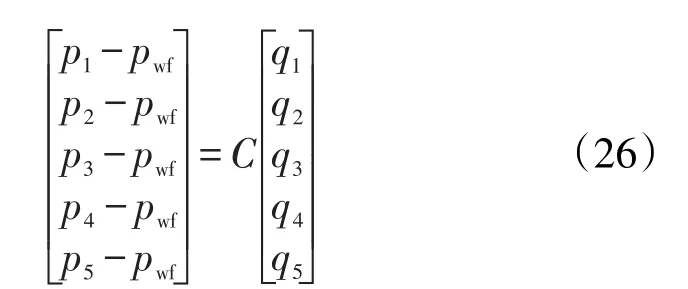
根据叠加原理，基于式（18），油藏中任意点处的压力是由所有裂缝离散势函数单元代数叠加求得，每个裂缝离散势函数单元间的相互流动由式（25）的裂缝中流体流动矩阵表示，耦合这2种流动得到压裂裂缝产量与压力的矩阵表达式为

压裂水平井总产量为

2　实例计算及敏感性分析

2.1实例计算

选取大庆长垣外围典型裂缝性致密油藏进行实例计算。基本参数包括：油层厚度为3.2m，原始地层压力为18MPa，井底流压为9MPa，基质渗透率为0.23×10-3μm2，地层原油体积系数为1.052，地层原油密度为0.826 g/cm3，地层原油粘度为1.45 mPa·s，有效水平井段长度为1 400m，压裂16段，平均每段2～3簇压裂裂缝，平均人工裂缝半长为154 m，井筒半径为0.05m，天然裂缝密度为5条/m，天然裂缝与井筒方向的夹角约为32°，该区块平均应力敏感系数为0.033，根据所建立的裂缝性致密油藏多角度裂缝压裂水平井产能计算方法，编制了相应的程序计算初始稳定产量，根据区块天然裂缝表征参数得到了等效渗透率张量，其中最大主渗透率方向与井筒夹角为30°。

计算结果表明：在不考虑天然裂缝和考虑天然裂缝的条件下，压裂水平井的产量分别为27.8和40.2m3/d，与实际初期产量（35.4m3/d）的计算误差分别为21.5%和13.6%；而考虑微地震解释裂缝形态、天然裂缝和应力敏感对产量的影响，利用新方法预测的压裂水平井产量与实际情况相差较小，计算误差仅为6.2%。另外，通过计算模型求解地层压力分布，得到的压力场分布形态（图2）说明裂缝处压力下降明显且压力分布跟裂缝形态密切相关。

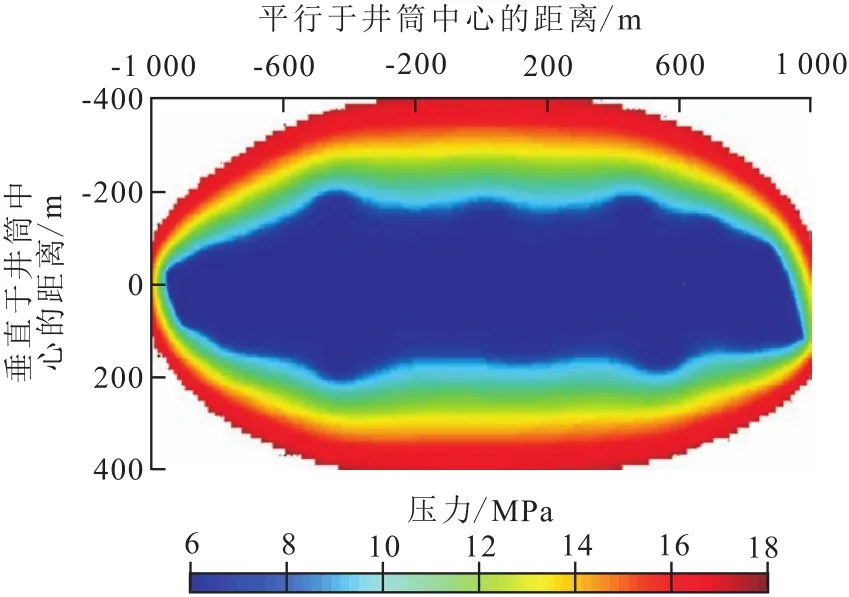
图2　压裂裂缝压力场Fig.2　Pressure field of the fractured cracks

2.2产能影响因素敏感性分析

利用新建方法，对储层最大主渗透率方向与压裂裂缝的夹角、裂缝导流能力、裂缝条数和应力敏感等4个影响压裂水平井产量的主要因素进行分析。

储层最大主渗透率方向与压裂裂缝的夹角由产量随储层最大主渗透率方向与压裂裂缝的夹角的变化结果（图3）可知，夹角越大，产量越大，但裂缝条数不同，夹角对产量的影响程度也不同，压裂直井最大产量与最小产量的比值大于压裂水平井。因为最大主渗透率方向与压裂裂缝的夹角越大，渗透率沿垂直于裂缝方向的渗透率越大，产量越大，而压裂水平井存在多条裂缝，间接增加了平行于裂缝方向的泄油面积，所以储层最大主渗透率方向与压裂裂缝的夹角对产量影响程度降低。

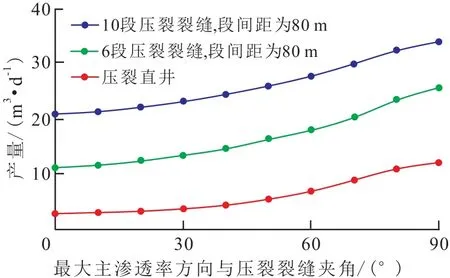
图3　最大主渗透率方向与压裂裂缝夹角对压裂直井和压裂水平井产量的影响Fig.3　Effectofanglebetweenmaximummajorpermeability and fracture direction on the production of the fractured verticaland horizontalwell

裂缝导流能力压裂水平井产量随裂缝导流能力的变化结果（图4）表明，产量随着裂缝导流能力的增加而增加，当裂缝导流能力增至100μm2·cm时，产量的增幅随着裂缝导流能力的增加变小。这是因为：对于致密油藏，基质向裂缝流动能力有限，裂缝内流体最大流动能力受到地层供液能力的限制。因此应当根据经济效益筛选支撑剂类型。

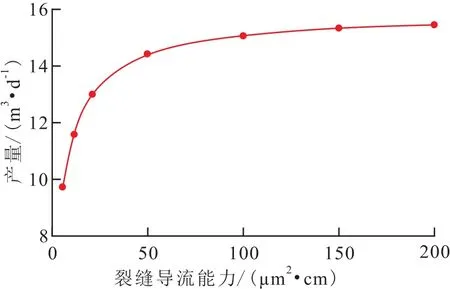
图4　裂缝导流能力与压裂水平井产量的关系Fig.4　Relationship between fracture conductivity and production of the fractured horizontalwell

裂缝条数分析压裂水平井产量与裂缝条数的关系（图5）可以看出，产量随着裂缝条数增加而增加，但是随着裂缝条数的进一步增加，产量的增幅变小。这是由于随着裂缝条数的增加，裂缝之间的干扰加剧所致。

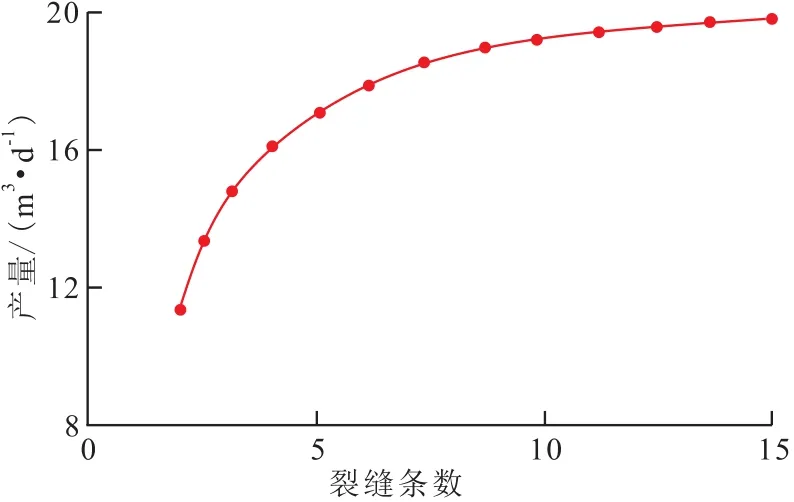
图5　裂缝条数与压裂水平井产量的关系Fig.5　Relationship between fracture numberand production of the fractured horizontalwell

应力敏感应力敏感对产量的影响结果（图6）表明，同一井底流压下，应力敏感系数越大，产量越小，同一应力敏感条件下，井底流压越小，产量曲线偏离不考虑应力敏感的直线距离越远，说明由应力敏感因素减少的产量越多。对于裂缝性油藏［5］，由于裂缝的存在，应力敏感程度比常规砂岩油藏要大，因此更应合理优化生产压差。

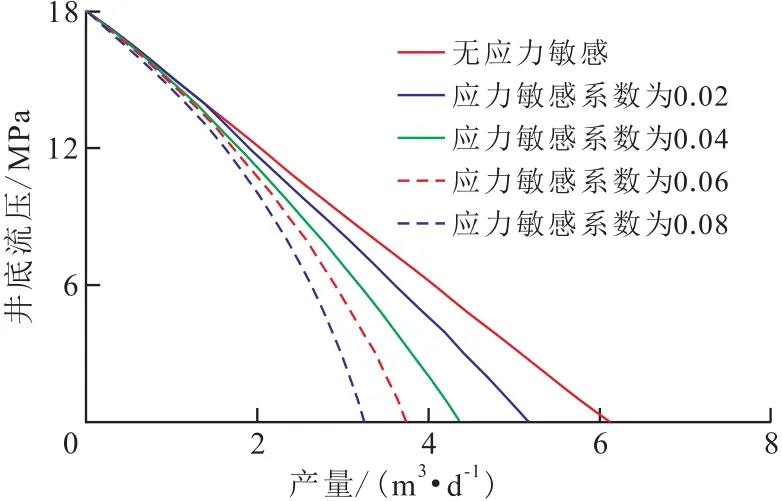
图6　不同应力敏感系数下对应的IPR曲线Fig.6　IPR curvesofdifferentstresssensitivity coefficients

3　结论

建立了考虑全渗透率张量的渗流数学模型，并采用线性变换将其转化为容易求解的拉普拉斯方程，基于离散的思想，利用势函数单元，建立了描述复杂压裂裂缝形态的半解析方法，并引入流体流动矩阵描述了人工裂缝内的流体流动，该方法能结合微地震资料和相关裂缝参数准确计算任意角度裂缝压裂水平井初期稳定产量。

压裂水平井产量随储层最大主渗透率方向与压裂裂缝的夹角的增大而增大，但裂缝条数不同，夹角对产量的影响程度不同，裂缝条数越大，夹角对产量的影响越小。设计压裂直井时，裂缝应尽量垂直于主渗透率方向；而多级压裂水平井裂缝与主渗透率方向存在一定夹角，但其对产能影响不大，如果是注水开发，存在一定夹角还可减缓采油井见水。

压裂水平井产量随裂缝导流能力的增加而增加，但对于致密油藏，基质向裂缝流动能力有限，裂缝内流体最大流动能力受到地层供液能力的限制，应当根据经济效益筛选支撑剂类型。

压裂水平井产量随着裂缝条数的增加而增加，但是随着裂缝条数的进一步增加，产量增幅变小，因此，根据经济评价原则对于一定长度的水平井存在最优裂缝条数。

应力敏感系数越大，产量越小，井底流压越小，因应力敏感因素减少的产量越多，对于裂缝性油藏，由于裂缝的存在，应力敏感程度比常规砂岩油藏要大，因此更要合理优化生产压差。

符号解释：

Kxx，Kxy，Kyx，Kyy——二维渗透率张量的4个分量，μm2；x——垂直于井筒中心的距离，m；y——平行于井筒中心的距离，m；Keq——三维等效渗透率张量，μm2；Km——基质渗透率张量，μm2；i——天然裂缝编号；nnf——天然裂缝总数；Keqi——第i条天然裂缝的渗透率，μm2；βi——第i条天然裂缝的倾向，rad；γi——第i条天然裂缝的倾角，rad；bi——第i条天然裂缝的开度，μm；li——第i条天然裂缝的间距，μm；Keqxy——二维等效裂缝渗透率，μm2；αi——第i条天然裂缝与x轴的夹角，rad；Kmx——基质在x方向的渗透率，μm2；Kmy——基质在y方向的渗透率，μm2；p——地层压力，MPa；x1——等效各向同性地层垂直于井筒中心的距离，m；y1——等效各向同性地层平行于井筒中心的距离，m； K——考虑天然裂缝影响的基质渗透率——人工裂缝处压力，MPa；q——裂缝单元流入量，m3/d；μo——地层原油粘度，mPa·s；Bo——地层原油体积系数；h——储层厚度，m；ξ——等效垂直于井筒中心的距离，m；η——等效平行于井筒中心的距离，m；C——流体流动矩阵；pj（x，y）——离散势单元中心压力函数，MPa；j——人工裂缝编号；qj——离散势单元中心流量函数，103m3/s；r1j——任意点与人工裂缝左端点距离，m；r2j——任意点与人工裂缝右端点距离，m；xfj——微元体裂缝半长，m；x0j——射孔点到井筒的水平距离，m；θj——人工裂缝与x轴的夹角，rad；y0j——射孔点到井筒的垂直距离，m；K0——基质原始渗透率，μm2；αk——应力敏感系数，1/MPa；p0——原始地层压力，MPa；pstr——考虑应力敏感无因次压力函数；r——任意点到裂缝中心距离，m；pstrj（x，y）——考虑应力敏感裂缝单元无因次压力函数；pwf——井底流压，MPa；Kf——裂缝渗透率，μm2；wf——人工裂缝宽度，m；xwf——人工裂缝中心与井筒距离，m；ro——等效网格半径，m；rw——井筒半径，m；Δx——人工裂缝微元长度，m；Δh——人工裂缝微元高度，m；pj（xe，ye）——裂缝微元体拟压力函数，MPa，j=1，2，…，N×M。

［1］ 林森虎，邹才能，袁选俊，等.美国致密油开发现状及启示［J］.岩性油气藏，2011，23（4）：25-30，64. Lin Senhu，Zou Caineng，Yuan Xuanjun，et al.Status quo of tight oil exploitation in the United States and its implication［J］.Lithologic Reservoirs，2011，23（4）：25-30，64.

［2］ 贾承造，邹才能，李建忠，等.中国致密油评价标准、主要类型、基本特征及资源前景［J］.石油学报，2012，33（3）：343-350. Jia Chengzao，Zou Caineng，Li Jianzhong，et al.Assessment criteria，main types，basic features and resource prospects of the tight oil in China［J］.Acta PetroleiSinica，2012，33（3）：343-350.

［3］ 贾承造，郑民，张永峰.中国非常规油气资源与勘探开发前景［J］.石油勘探与开发，2012，39（2）：129-136. Jia Chengzao，Zheng Min，Zhang Yongfeng.Unconventionalhydrocarbon resources in China and the prospectofexploration and development［J］.Petroleum Exploration and Development，2012，39 （2）：129-136.

［4］ 魏海峰，凡哲元，袁向春.致密油藏开发技术研究进展［J］.油气地质与采收率，2013，20（2）：62-66. WeiHaifeng，Fan Zheyuan，Yuan Xiangchun.Review on new advances in foreign tight oil development technology and their enlightenment［J］.Petroleum Geology and Recovery Efficiency，2013，20（2）：62-66.

［5］ Van Golf-Racht T D.Fundamentals of fractured reservoir engineering［M］.Elsevier Texas：Elsevier Science Ltd.，1982：48-52.

［6］ OdaM.Permeability tensor for discontinuous rockmasses［J］.Geotechnique，1985，32（1）：483-495.

［7］ 刘建军，杜广林.裂缝性砂岩油藏流固耦合渗流的等效介质模型［J］.中国海上油气：地质，2003，17（3）：204-210. Liu Jianjun，Du Guanglin.An equivalentmodelof fluid-solid coupling flow in fractured sandstone reservoir［J］.China Offshore Oil and Gas：Geology，2003，17（3）：204-210.

［8］ 刘建军，张盛宗，刘先贵，等.裂缝性低渗透油藏流-固耦合理论与数值模拟［J］.力学学报，2002，34（5）：779-784. Liu Jianjun，Zhang Shengzong，Liu Xiangui，etal.Theory and simulation of fluid-solid coupling flow through low permeability fractured oil reservoir［J］.Acta Mechanica Sinica，2002，34（5）：779-784.

［9］ Lee SH，Jensen C L，Lough M F.An efficient finite difference model for flow in a reservoirwith multiple length-scale fractures ［R］.SPE 56752，2007.

［10］张德良，张烈辉，赵玉龙，等.低渗透气藏多级压裂水平井稳态产能模型［J］.油气地质与采收率，2013，20（3）：107-110. Zhang Deliang，Zhang Liehui，Zhao Yulong，etal.Study on steady productivity of fractured horizontal well in low permeability gas reservoir［J］.Petroleum Geology and Recovery Efficiency，2013，20（3）：107-110.

［11］王欢，廖新维，赵晓亮，等.超低渗透油藏分段多簇压裂水平井产能影响因素与渗流规律——以鄂尔多斯盆地长8超低渗透油藏为例［J］.油气地质与采收率，2014，21（6）：107-110. Wang Huan，Liao Xinwei，Zhao Xiaoliang，et al.A study on productivity and flow regimes of segmented multi-cluster fractured horizontal well in ultra-low permeability reservoir-a case of Chang8 ultra-low permeability reservoir in Ordos Basin［J］.Petroleum Geology and Recovery Efficiency，2014，21（6）：107-110.

［12］陆程，刘雄，程敏华，等.页岩气藏开发中的水力压裂水平井敏感参数分析［J］.特种油气藏，2013，20（5）：114-117. Lu Cheng，Liu Xiong，Cheng Minhua，et al.Sensitivity analysis of hydraulic fracturinghorizontalwells in shalegas reservoir［J］.SpecialOil&Gas Reservoirs，2013，20（5）：114-117.

［13］吕志凯，冀光，位云生，等.致密气藏水平井产能图版及应用［J］.特种油气藏，2014，21（6）：105-108. Lv Zhikai，JiGuang，WeiYunsheng，etal.Horizontalwell production type-curve and its application in tightgas reservoirs［J］.SpecialOil&GasReservoirs，2014，21（6）：105-108.

［14］Guo Boyun，Yu Xiance，Mohammad Khoshgahdam.A simple analyticalmodel for predicting productivity ofmultifractured horizontalwells［R］.SPE 114452，2009.

［15］孔祥言.高等渗流力学［M］.合肥：中国科学技术大学出版社，2010：189-193. Kong Xiangyan.Advanced mechanics of fluids in porous media ［M］.Hefei：University of Science and Technology ofChina Press，2010：189-193.

［16］Zhu D，Magalhaes F，ValkóPP.Predicting the productivity ofmultiple-fractured horizontalgaswells［R］.SPE 106280，2007.

［17］Lin Jiajing，Zhu Ding.Predicting well performance in complex fracture systemsby slab sourcemethod［R］.SPE 151960，2009.

［18］Peaceman DW.Interpretation ofwell block pressures in numerical reservoir simulation［R］.SPE 16976-PA，1990.

编辑常迎梅

A com putationalmethod for productivity of arbitrary angular fractured horizontalwell in tightoil reservoirs

Fang Sidong1，Zhan Jianfei2，Huang Shijun1，He Congge3

（1.College ofPetroleum Engineering，China University ofPetroleum（Beijing），Beijing City，102249，China；2.Exploration and DevelopmentResearch InstituteofDaqing Oilfield Company Ltd.，PetroChina，Daqing City，Heilongjiang Province，163712，China；3.Research InstituteofPetroleum Exploration and Development，PetroChina，Beijing City，100083，China）

Multi-staged fracturing for the horizontalwell is the key technique of tightoil reservoir development.Due to the complexity of the in-situ stress and the impactof natural fractures，there is usually a certain angle between the hydraulic fractures and thewellbore，whichmakes the production forecastof the fractured horizontalwell very difficult.Based on the equivalent permeability tensor theory in naturally fractured reservoir，a steady flow mathematicalmodel has been established in the tight oil reservoir with full permeability tensor.By combining the half-analyticalmethod that considering stress sensitivitywith potential superposition principle，a discrete potential function unitof the flow from matrix to artificial fractureswas formed.The flow in the fractures is considered as linear flow among the discrete units，and thematrix and fracture flow are coupled and solved.A computationalmethod for productivity ofarbitrary angular fractured horizontalwell under the condition of the natural fractureswas given.The resultofa practical case shows that the error between the computing results and the field data is less than 7%for considering the effect of the angle of the natural and artificial fractures. Sensitivity analysis indicates that the angle between the primary permeability and the hydraulic fracture has a significant impacton thehorizontalwellproductivity.

tightoil reservoir；fullpermeability tensor；fractured horizontalwell；stress sensitivity；productivity

TE313.8

A

1009-9603（2015）03-0084-06

2015-03-04。

方思冬（1988—），男，四川南充人，在读博士研究生，从事低渗透油藏油藏工程和数值模拟研究。联系电话：18810415481，E-mail：jbwolfgang@163.com。

国家自然科学基金“特低渗油藏天然缝与人工缝耦合作用的渗流机理与模型”（51174215/E0403）。