在思维驱动中进行问题的有效探究
【摘 要】物理作为一堂重要的理论探究课,怎样把理性的思辨展现为感性的体验,在略显枯燥的理论探究中激扬思维、涤荡心灵,这考验着教师的教学智慧。有效驱动学生的思维,显得至关重要。
【关键词】高中物理;激发思维;教学设计
【中图分类号】G633.7 【文献标志码】A 【文章编号】1005-6009(2015)34-0049-03
【作者简介】浦建军,江苏省锡东高级中学(江苏无锡,214105)教师。
一、问题驱动,激发学生思维
问题1:我们可以怎样表示匀速直线运动的位移与时间的关系?
生:公式表示,x=vt。图像表示,x-t图像反映了任意时刻的位移。
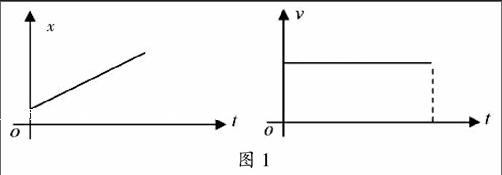
师:请画出x-t图像及对应的v-t图像(如图1)。v-t图像能否表示位移与时间的关系?
生:根据公式可知,图像中矩形的面积可以表示时间t内的位移。
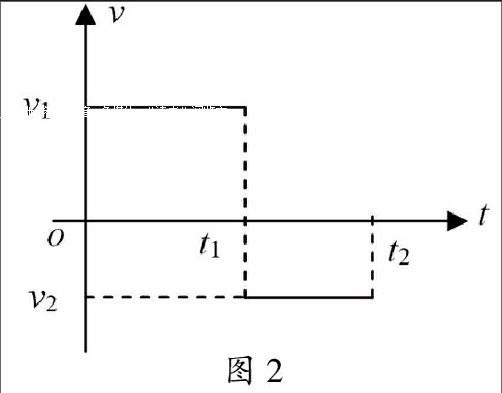
师:在图像中画出矩形。位移是矢量,有正负,图像中如何体现正负?请结合图2分析。
生:由图像可知,物体沿某方向匀速直线运动时间t1后,又返回走了t2时间,物体的位移应是x=v1t1-v2t2,从图像看刚好是上下两个矩形面积之差。v-t图像中面积的正负可以表示位移的正负。
把物理公式与函数图像或几何图形结合思考,体现了“数形结合”的思想。数与形两者是统一并可以相互转化的,“以数解形、以形助数”是解决问题的一种新思路。
【设计意图】高一新生刚入学不久,还没有完成从感性认识向理性认识、形象思维向抽象思维的过渡,逻辑思维能力、知识应用水平、推导运算能力等方面都处于较低水平。从学生最熟悉的匀速直线运动开始探讨位移与时间的关系,是基于学生的认知基础,给学生搭建认知的“脚手架”。从公式x=vt和图像两个不同层面表述,既能反映出学生知识结构的完整性,也能表现出学生思维的开放性。v-t图像的追问则是引导学生从数形结合的思路研究问题,融入了思维方法教育,数形结合的新思路较好地激发了学生的思维,为下面的研究做好了知识、方法、心理的铺垫。
二、问题辩论,深化学生思维
问题2:本章主要研究匀变速直线运动,我们又可以怎样表示匀变速直线运动的位移与时间的关系?
生:变速运动的位移应该是平均速度乘以时间,x=vt。
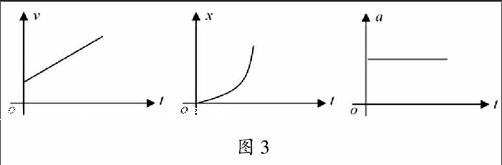
师:请画出图像(如图3),所画图像是怎样表示位移与时间的关系的?
生:匀加速直线运动中,相同时间内的位移越来越大,x-t图像的斜率是变化的,所以是曲线,同样能反映任意时刻的位移。
师:从数形结合的角度考虑,你画的曲线可能是数学中的什么函数?
生:匀速直线运动的v-t图像中矩形面积可以表示位移,据此我认为匀变速直线运动中也应该有一个矩形,匀变速运动的加速度是不变的,所以a-t图像中矩形可以表示位移。
师:你已经学会了使用类比的方法研究问题,很好。匀速直线运动的v-t图像中矩形面积表示位移是从数形结合即从公式到图像得出的。你可以据此证明自己的判断是否正确吗?
生:a-t图像中矩形面积为at,而v=at,不代表位移。根据类比,我觉得v-t图像中的梯形面积可以表示位移。
师:在v-t图像中画出梯形(如图4),你的理由是什么?
【设计意图】从最简单的匀速直线运动到较为复杂的匀变速直线运动,让学生在“形异质同”的比较中进行思维碰撞,大胆猜想,驱动学生主动思考,利用类比思想猜想可能的结论。通过师生对话,在问题的思辨中逐步深化认识。
问题3:有两辆车,甲车做初速度为v0的匀变速直线运动,乙车做速度为v0的匀速直线运动。两者的速度-时间图像如图5。在时间t内,乙车的位移在图中如何表示?
生:用矩形面积表示。
且因甲车的平均速度较大,相同时间内,甲车位移大于乙车位移。
师:若乙车运动变为两段匀速直线运动,乙车位移怎样表示?四段匀速直线运动呢?
生:两个矩形面积之和,四个矩形面积之和。
师:若乙车运动变为8段匀速直线运动,乙车位移怎样表示?16段呢?32段呢?100段呢?
生:8个矩形面积之和、16个矩形面积之和、32个矩形面积之和、100个矩形面积之和。
教师根据学生回答,在图5中画出每个问题的图像(如图6),标注出每个矩形。
师:你有什么新发现?
生1:不管怎么分,由于是匀速直线运动,总位移等于所有矩形面积之和。
生2:我从老师画出的v-t图像中发现,矩形的个数越多,越接近梯形的面积。
生3:我认为不管怎么分,所有矩形的面积之和应该小于梯形面积。
师:你们的“发现”都有道理,有的同学是从直观的图像得出的结论;有的同学是在图像的基础上进一步联想,猜想出的结论;还有的同学是在类比迁移中深思熟虑的结果。就以100段为例,大家发现矩形的宽已经无法在图中画出了,它是一个很狭长的矩形。假如分成1000段,矩形的宽更小了。假如可以分成足够多的等分,矩形的宽就成了“点”,矩形就成了我画的一条条“竖线”。大家觉得这些“竖线”的面积累加起来等于梯形面积吗?此时乙车的运动与甲车的运动有什么关系呢?
生:所有矩形面积之和等于梯形面积。匀变速直线运动的位移可用v-t图像中图线与时间轴围成的图形面积表示。
【设计意图】物理教学应基于学生的认知建构过程,特别是思维可视化的教学方式更利于展现学生的思维路径,促进学生看清本质,掌握要点。为突破“匀变速直线运动的位移可以用图像中图线与时间轴围成的面积表示”这一教学难点,教师可通过设置有阶梯性的问题链,让学生“可触摸、可比较”,同时层层深入,激起一个个思维的浪花,实现学生求知欲望的满足,从而有效拉近探究的新问题与学生原有知识固着点的“潜在距离”,切合学生的“最近发展区”,使得学生的观察和思维能力得到积极而有序的提升,也能够很好地培养学生的思维。
三、问题拓展,开阔学生思维
问题4:请你从数形结合的角度,求出图像中图线与时间轴围成的图形面积即位移。
生:从梯形面积公式可以得出x=v0t+at2。
师:数形结合就是对几何图形进行图形的分割与组合,大家可以相互协作,比一比谁想到的方法最多。
师生探讨,还可以有以下方法:
师:我们充分利用数形结合的思想,得到了匀变速直线运动的位移与时间的关系有多种定量表达的结论,从这些结论中,你又有什么新的发现?
生:我从表达式中发现,平均速度有不同表达。
x=vt=t
刚才在图像中的曲线应该是抛物线的一部分。
师:很好!物理图像一般与数学函数有着紧密联系。在匀变速直线运动中,平均速度有着不同表达,大家要灵活应用。如果一个物体的速度是均匀增大的,那么,它在某段时间里的平均速度就等于初速度和末速度之和的一半,即v=。
【设计意图】“从图像的面积求解推导位移公式”是教学的重点。教材中只是简单地从梯形面积公式推导出位移公式,忽视了这部分教学内容的潜在价值。问题4是具有顺延、伸展特征的扩展性问题,要求学生不就事论事、就题论题,而是本着促使学生思维向新的广度和深度发展,从生长点和提高点上设计问题,强调学生从数形结合的思路对几何图形进行分割、组合。学习需要开阔的视野、灵动的思维、扎实的基础,获得积极的情感体验时学生的学习力在无形中也得到了有效提升。
学生在后续的学习中还会发现,本节课“不经意间”已经解决了匀变速直线运动的另两个规律——平均速度与时间中点速度的关系、速度与位移的关系,他们强烈体验到具有开阔而灵活的思维才可以灵巧而高效地学习。
【参考文献】
[1]佐藤学.教师的挑战:宁静的课堂革命[M].钟启泉,陈静静,译.上海:华东师范大学出版社,2012.
[2]高凌飚,陈冀平,张军朋.物理教学与学业评价[M].广州:广东教育出版社,2005.
[3]钱玲,喻潜安.教学设计理论与实践[M].北京:教育科学出版社,2012.

