三角形机翼参数化有限元网格划分与调整方法
许孟辉,邱志平
(北京航空航天大学航空科学与工程学院,北京100191)
三角形机翼(三角翼)是轻型飞机及歼击机的典型代表构型之一.作为提高设计质量和缩短设计周期的重要途径,计算机仿真技术及相关软件系统在三角翼的初步设计和详细设计中得到了大量应用[1-3].而当前三角翼结构的有限元建模耗时低效,已成为限制其结构分析、设计与优化整体效率的瓶颈问题之一[4-7].参数化有限元建模是提高有限元模型构建效率必不可少的手段之一.
MSC.Patran是国际航空航天器结构分析领域的基准软件,也是工业领域内著名的并行框架式有限元前后处理及分析仿真系统.用户可利用其强大的 PCL(Patran Command Language)语言[6-14]和编程函数库将自行开发的应用程序、功能及应特殊要求开发的内容直接嵌入MSC.Patran的框架系统,或单独使用或与其他系统联合使用.本文以其为平台引入三角翼结构的参数化有限元网格快速建立与调整方法,提高结构分析、设计与优化效率.
刘虎等[5-7]研究了机身/机翼结构的参数化几何建模方法与参数化有限元建模方法,虽可以人工控制有限元节点与单元信息,但机翼结构的参数化有限元建模的前提是实现其参数化几何建模.舒恪晟等[8]以PCL语言开发了机身结构参数化几何建模软件,但并未实现对应有限元建模.陈小前等[9]与何祖平和王德禹[10]在实现结构参数化建模过程中以基于MSC.Patran的参数化几何建模为输入,通过网格种子实现结构的有限元建模,无法实现对有限元节点与单元的人工可控.陈博等[11]、匡国强和张晓晶[12]与刘斌等[13]以不同分析目的为指导借助PCL语言实现结构的快速建模与分析,但所提方法无法应用于三角翼结构的参数化有限元建模,并且有限元的节点与单元信息可控性差.为克服结构参数化有限元网格划分对参数化几何建模的依赖,并且有效控制有限元节点与单元信息(位置或编号),本文以典型多梁式三角翼结构为对象探讨其参数化有限元网格划分方法.
1 三角翼及其预处理
三角翼(如图1所示)结构由主机翼(P11、P12和P13)、前缘襟翼(P2)和内外侧副翼(P3和P4)组成,其中主机翼为厚蒙皮多墙式结构,主要包括翼梁、纵墙、翼肋、桁条和蒙皮等结构件.翼梁和纵墙承受机翼总体剪力和弯矩,并通过固支于机身而获得支反力和支反弯矩;翼肋维持机翼剖面所需形状,将自身及收集到的气动载荷传递给蒙皮、翼梁/墙腹板组成的翼盒;蒙皮承受空气动力,并在蒙皮与翼肋有连接的情况下传递气动载荷给长桁和翼肋;桁条承受蒙皮局部气动力并将其传递给翼肋.
由于机翼前后缘的翼型非常薄,腹板单元若按实际取,常常是畸形的,造成刚度矩阵奇异.一般情况下,按照剖面积不变的原则,将平面外形向内适当收缩,而翼型高度略微增加,如图2所示,满足剖面积S2+S3=S1.这样,既不会使刚度矩阵奇异,又不会造成大的误差[15].

图1 三角翼示意图Fig.1 Sketch of a delta wing

图2 修正原理图Fig.2 Principle of amendment
通过剖面积等效处理后三角翼结构气动外形如图3所示,上下翼面一般为曲面,外形线为曲线时可采用不同精度的分段近似.
本文以图3所示气动外形为输入,考虑方法的通用性,将其划分为如图1所示的6个部分,各部分有限元网格独立建立,最后组成一个完整网格.通过选取表1所列之几何参数,实现三角翼结构参数化网格划分与调整.

图3 气动外形示意图Fig.3 Sketch of aerodynamic configuration

表1 几何参数列表Table 1 Geometric parameters list
2 参数化网格划分
为满足对不同精度有限元网格的需求,本文实现机翼展向、弦向和垂向3个方向的单元尺寸的参数化.由于网格单元可以通过节点按照特定顺序连接而自动生成,节点的生成与管理是整体参数化网格划分的关键.对于由不同区域有限元网格组合而形成整体有限元网格的大型结构而言,为预防出现编号重复或编号不协调,规定节点与单元的编号格式是非常必要的.同时,满足一定格式的编号方法对实现节点和单元的管理(如单元分组等)十分有益.
2.1 节点编号定义
节点本质上可视为二维数组,分别存储节点编号和节点空间位置,其中节点编号规则由设计人员自定义实现,节点空间位置信息由几何求交运算或数值计算确定.为方便确定三角翼有限元网格的节点空间位置,在不同分区建立适当的局部坐标系,如图1所示.
根据有限元建模“由大及小划分,以小代大模拟”的基本思路,图1中三角翼结构的不同分区可视为一种粗略的有限单元划分格式.进一步,在不同分区内部,以翼肋为切入点对节点进行编号,通过翼肋与其他各个结构件的相交关系定义节点编号显示格式:
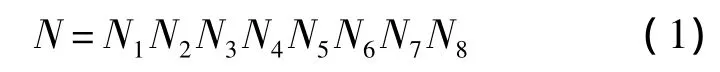
对应的节点编号数值计算格式为


图4 左侧机翼ab梁腹板的节点编号Fig.4 Numbers of nodes on web of beam ab of left wing
式中:N1为机翼位置序号,左侧机翼取值为1,右侧机翼取值为2;N2N3为不同分区内的翼肋序号.区域P11编号范围为0~19;区域P12编号范围为20~29;区域P13编号范围为30~39;区域 P2编号范围为40~49;区域P3编号范围为50~59;区域P4编号范围为60~69;N4为翼肋间节点序号,取值范围为0~9;N5N6为不同分区内的梁/墙序号;N7表示梁/墙间节点序号,取值范围为0~9;N8为上下蒙皮间节点序号,取值范围为0~9,上蒙皮节点取值为0,下蒙皮节点取值为9,中间节点取值范围为1~8.
根据式(1)所确定的节点编号格式,图4给出了左侧三角翼ab梁腹板的节点编号.需要注意的是,编号格式中各变量的取值范围确定了式(1)的实际适用范围,可根据具体问题予以调整.
2.2 单元编号定义
网格单元通过满足自定义编号规则的网格节点按一定顺序连接而自动生成.根据网格节点编号规则,单元编号显示格式定义为
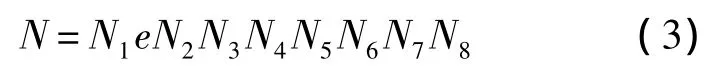
相应的数值计算格式为
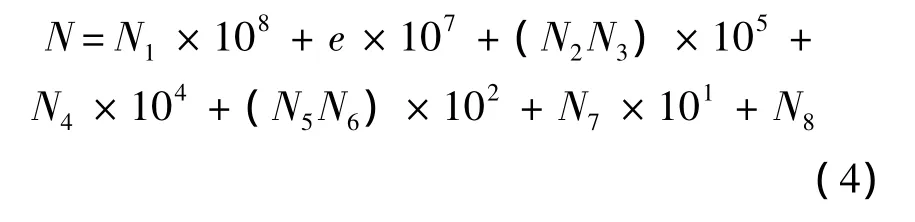
式中:Ni含义与式(1)和式(2)中对应含义相同,i=1,2,…,8;e为单元类型序号,规定:
1)壳单元:蒙皮取值为0,梁/墙腹板取值为1,肋腹板取值为2,斜肋(位于区域 P13和P2)腹板取值为3.
2)杆单元:梁/墙/缘条与桁条取值为4,肋缘条取值为5,斜肋缘条取值为6.
值得注意的是,在三角形单元和四边形单元过渡区内,为避免单元编号非协调性,本文对三角形单元编号进行了修正,如将单元编号中的N2N3(或N5N6)以N2N3+20(或N5N6+20)代替.
2.3 网格划分
2.3.1 骨架布局的确定
在自定义气动外形所对应的主受力盒区P11中,设计人员给定局部坐标系下的梁/墙位置参数及翼肋位置参数,在加工工艺等约束下,需要定义翼肋沿x方向贯穿位置,即通过图5中y与y1、y2的自定义逻辑关系计算翼肋贯穿位置的x坐标值,以确定机翼骨架几何布局满足设计人员的要求.本文引入工艺参数a,通过初步判断翼肋贯穿截止坐标并依此建立初步有限元网格.借助第2.3.4节网格细化操作可确定翼肋最终的理想贯穿截止位置.
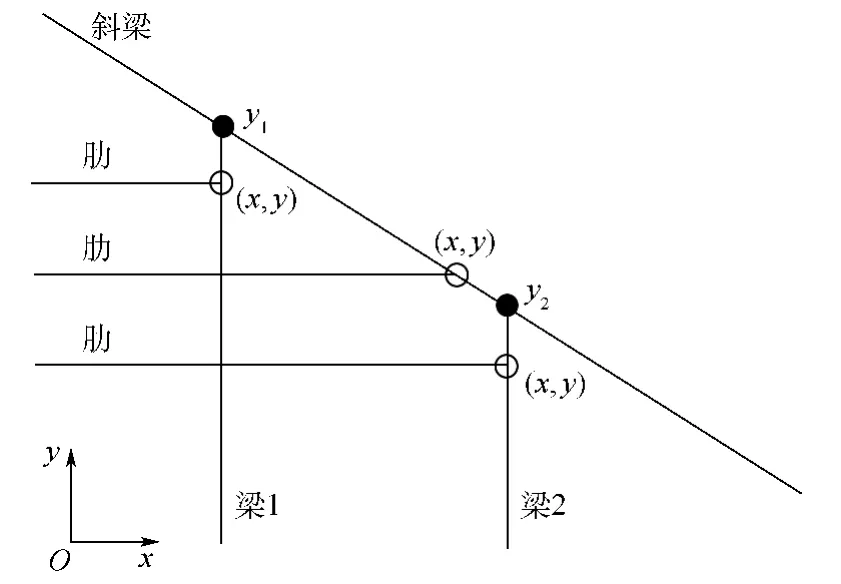
图5 肋端点位置图Fig.5 Sketch of rib end locations

2.3.2 节点布置的确定
在给定三角翼所有几何参数的情况下,其不同分区内由梁/墙、翼肋、桁条等围成的单位分区主要有5种情形,在上下翼面间的中面处的投影如图6所示.因此,需要分别确定在此5种不同情形下的节点布置方式.
引入对应骨架布局等逻辑判断的形状矩阵M2×5,该矩阵的每一列分别依次存储从左下角顶点坐标起沿逆时针方向的各顶点坐标,若无对应顶点,则初始化对应元素为0,如图7所示.

图6 骨架结构的中面投影单位分区形状Fig.6 Shapes of unit region of projections of skeleton components on middle plane
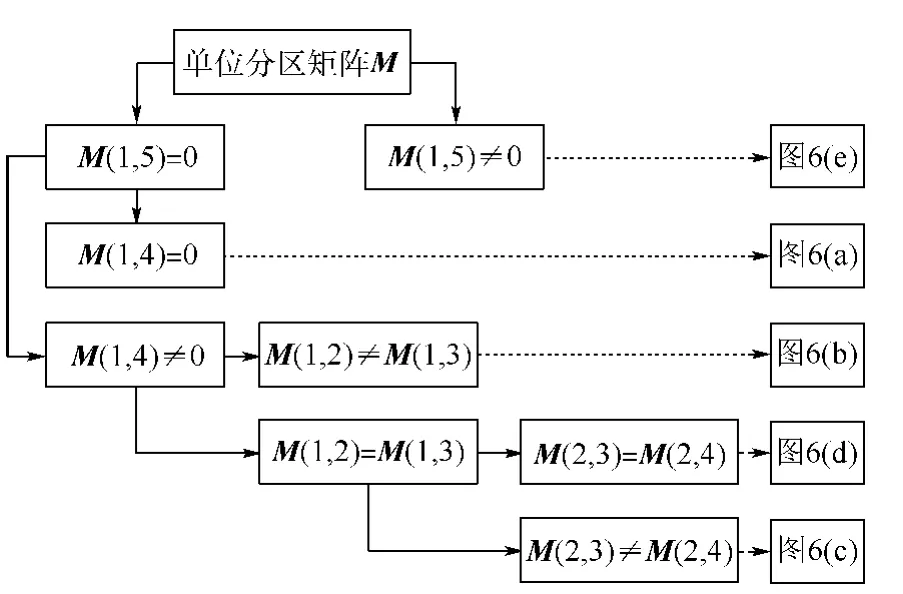
图7 形状矩阵与单位分区的关系Fig.7 Relationships between geometrical matrix and unit regions
通过形状矩阵M确定不同单位分区的节点布置方式.值得注意的是,决定节点间距的单元尺寸是设计人员输入参数.因此,需要引入非矩形单位分区的节点布置截止原则.以图6(a)所示机翼中面的三角形单位分区为例,基于弦向单元尺寸由左向右依次布置底边的节点,当待布置节点与右下角顶点之间的距离满足一定关系,则待布置节点取作右下角顶点.进一步,以底边弦向节点为基础,逐列布置每个底边节点对应的展向节点,当待布置展向节点与底边节点对应的斜边节点(通过底边节点的垂线与斜边的交点)之间的距离满足一定关系时,待布置节点取作底边节点对应的斜边节点.而距离关系可以由设计人员通过单元长细比等参数自定义.通过三角翼中面的布置节点投影至上下翼面,并可以根据垂向单元尺寸参数确定腹板位置处的节点,最后将中面辅助节点删除.
2.3.3 有限元网格划分
按照指定顺序依次连接已有的节点可以生成相应的有限单元并分组,在该过程中通过弦向相邻2列的节点数目之间的关系确定四边形单元与三角形单元的具体节点连接方式.对于相邻单位分区间的单元连接则借助相应形状矩阵完成.进一步,由式(4)赋予相应单元编号,至此已建立初步有限元网格.根据机身两侧三角翼的对称性,另一侧三角翼的有限元网格可以通过两机翼间距对称生成,并赋予相应的节点编号和单元编号.
2.3.4 有限元网格细化
基于已建立的三角翼有限元网格,设计人员可以对其完成进一步细化,以2个梁/墙编号和2个翼肋编号作为参数完成机翼开口设置,以翼肋贯穿位置调整参数确定翼肋理想贯穿位置,以梁/墙编号为参数完成相应的桁条等网格划分,这些网格细化操作均可以通过删除已有单元与部分关联节点完成.
值得注意的是,本文以三角翼结构的有限元网格划分为重点,不同分区间的连接、单元属性、边界条件及载荷等的设置则仍通过MSC.Patran完成.
3 参数化网格调整
在很多情形下,设计人员期望以当前有限元网格为基础以较小代价完成网格一定幅度的调整.如内/外侧副翼中翼肋的位置调整、适应不同飞行状态的前缘襟翼及内外侧副翼等活动舵面的旋转角度调整等.
3.1 位置调整
内/外侧副翼中翼肋的位置调整是通过指定翼肋序号与待移动新位置坐标2个参数完成.值得注意的是:①限于主受力盒区中梁、墙、翼肋间相交的关系复杂,不宜进行翼肋和梁/墙位置的局部调整;②由于结构件的位置调整是通过节点移动完成,为避免引起气动外形的大幅变化,位置调整仅适用于一定距离内的结构件位置移动.而大幅度的结构件位置调整亦可以通过结构件重新参数化网格划分完成.
3.2 角度调整
在不同飞行状态下,前缘襟翼和内/外侧副翼的旋转状态是不同的.为快速建立不同飞行状态下三角翼结构的有限元网格,可以通过旋转角度参数实现活动舵面有限元网格的角度调整.
4 实例
基于所提参数化网格划分方法,本文借助PCL语言开发了三角翼结构参数化有限元网格划分模块,如图8所示.并对图3所示的三角翼结构进行参数化有限元网格划分.
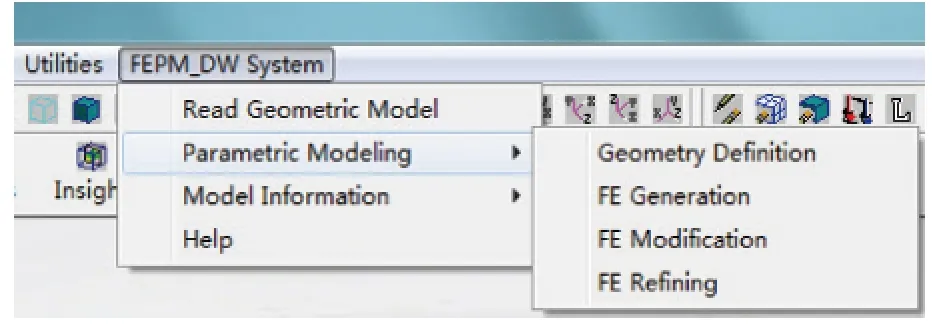
图8 参数化网格划分模块Fig.8 Parametric meshing module
4.1 有限元网格划分
在给定2种不同的几何参数与有限元尺寸参数前提下,所生成的三角翼结构初始有限元网格如图9所示,对应的骨架有限元网格如图10所示.
在第2种参数设置下,通过给定开口参数、翼肋贯穿位置参数及桁条对应梁/墙序号参数,可以得到细化的骨架有限元网格,如图11所示.

图9 情形1和情形2下的机翼有限元网格Fig.9 Finite element(FE)meshing of wing in Case 1 and Case 2
在建立有限元过程中,相应的分组同步完成,如图12所示.

图10 情形1和情形2下的骨架有限元网格Fig.10 FE meshing of skeleton in Case 1 and Case 2
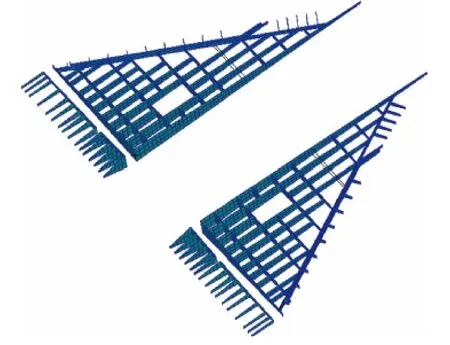
图11 细化的骨架有限元网格Fig.11 Refined FE meshing of skeleton

图12 自动分组结果Fig.12 Consequences of auto-group
4.2 有限元网格调整
通过给定内/外侧副翼的翼肋序号与待移动新位置参数,可以对相应结构件进行位置调整,如图13所示.
通过给定前缘襟翼、内/外侧副翼的旋转角度参数,可以建立活动舵面在调整角度后的有限元网格,如图14所示.

图13 副翼的肋位置调整Fig.13 Location modifications of ribs of aileron

图14 舵面的角度调整Fig.14 Angle modifications of control surfaces
5 结论
本文以多梁式三角翼结构为对象探索了参数化有限元网格划分和调整方法,定义了统一简洁的有限元节点和单元编号规则,引入翼肋贯穿截止准则及形状矩阵完成单位分区的有限元网格划分,通过网格细化完成开口设置、翼肋贯穿截止位置修正及桁条网格划分,并进一步探索了内/外侧副翼的翼肋位置小幅调整及旋转舵面的角度调整方法.本文探索为三角翼的结构分析与多学科设计优化奠定了基础,形成具有借鉴意义的结论如下:
1)本文所定义有限元节点与单元的编号规则协调统一实用,便于实现节点和单元的后续操作,如开口设置等.
2)所引入之翼肋贯穿截止准则简便,综合网格细化方法,满足任意输入参数下机翼内部构型的判断与修正.
3)所定义之形状矩阵M有效简化了有限元节点布置、单元生成及不同单位分区间单元连接,对不同形式的单位分区具有普遍适用性.
4)活动多面的角度调整功能有利于开展不同飞行状态下的结构分析等;但限于所输入之几何气动外形,内外侧副翼的翼肋位置调整适用于小幅调整.
5)由于平直机翼气动外形相对规则,本文方法适用于平直机翼的有限元参数化网格划分与调整.
References)
[1] Roberts R W,Canfield R A,Blair M.Sensor-craft structural optimization and analytical certification,AIAA-2003-1458[R].Reston:AIAA,2003.
[2] Mike R.MD Nastran 2006 DMAP programmer’s guide[M].Spmta Ana:MSC Software Corporation,2005:xii-xiv.
[3] Hermann T M,Mamarthupatti D,Locke J E.Postbuckling analysis of laminate composites utilizing commercial FEA software,AIAA-2005-0194[R].Reston:AIAA,2005.
[4]金海波,丁运亮.飞机概念设计中的外形参数化模型的研究[J].南京航空航天大学学报,2003,35(5):540-544.Jin H B,Ding Y L.Parameterization model for aircraft concept design[J].Journal of Nanjing University of Aeronautics and Astronautics,2003,35(5):540-544(in Chinese).
[5]白振东,刘虎,武哲.低可探测机身参数化造型与优化[J].北京航空航天大学学报,2007,33(12):1391-1394.Bai Z D,Liu H,Wu Z.Parametric modeling and optimization of low observability fuselage in aircraft conceptual design[J].Journal of Beijing University of Aeronautics and Astronautics,2007,33(12):1391-1394(in Chinese).
[6]罗明强,冯昊成,刘虎,等.民用飞机机翼结构快速设计及自动化调整[J].北京航空航天大学学报,2009,35(4):468-471.Luo M Q,Feng H C,Liu H,et al.Rapid wing structure design and automated scheme adjustment for civil aircraft[J].Journal of Beijing University of Aeronautics and Astronauctics,2009,35(4):468-471(in Chinese).
[7]罗明强,冯昊成,刘虎,等.机翼结构有限元的快速建模及自动化调整[J].北京航空航天大学学报,2011,37(6):680-684.Luo M Q,Feng H C,Liu H,et al.Rapid wing structural finite element modeling and automated adjustment[J].Journal of Beijing University of Aeronautics and Astronautics,2011,37(6):680-684(in Chinese).
[8]舒恪晟,金海波,姜琬.基于Patran二次开发的机身结构参数化建模[J].飞机设计,2011,31(2):30-32.Shu K S,Jin H B,Jiang W.Fuselage structure parametric modeling based on secondary development of Patran[J].Aircraft Design,2011,31(2):30-32(in Chinese).
[9]许林,郭中全,陈小前,等.基于PCL的高超飞行器结构参数化建模[J].计算机工程,2008,34(22):1-3.Xu L,Guo Z Q,Chen X Q,et al.Parametric modeling for hyper sonic vehicle structure based on PCL[J].Computer Engineering,2008,34(22):1-3(in Chinese).
[10]何祖平,王德禹.基于MSC.Patran二次开发的结构参数化建模及其集成开发环境[J].航海工程,2005(2):17-20.He Z P,Wang D Y.Parameterized modeling based on MSC.Patran and its integrated development environment[J].Ship &Ocean Engineering,2005(2):17-20(in Chinese).
[11]陈博,陈秀华,汪海.MSC.Patran二次开发及其集成开发环境[J].机械设计与制造,2007(7):71-73.Chen B,Chen X H,Wang H.Redevelopment of MSC.Patran and its integrated development environment[J].Machinery Design & Manufacture,2007(7):71-73(in Chinese).
[12]匡国强,张晓晶.基于MSC Patran参数化建模的飞艇蒙皮织物面内刚度预测[J].计算机辅助工程,2009,18(3):42-45.Kuang G Q,Zhang X J.In-plane stiffness prediction on fabric of airship envelop based on parameterized modeling of MSC Patran[J].Computer Aided Engineering,2009,18(3):42-45(in Chinese).
[13]刘斌,韩庆,钟小平.基于MSC.PCL的飞机结构稳定性系统开发[J].科学技术与工程,2010,10(28):7082-7088.Liu B,Han Q,Zhong X P.Development of aircraft structure’s stability system based on MSC.PCL[J].Science Technology and Engineering,2010,10(28):7082-7088(in Chinese).
[14] MSC.Patran PCL reference manual[Z].2007.
[15]叶天麟,周天孝.航空结构有限元分析指南[M].北京:航空工业出版社,1996:514-515.Ye T L,Zhou T X.Guide for finite element analysis of aerospace structures[M].Beijing:Aviation Industry Press,1996:514-515(in Chinese).

