高速列车比例车体谐响应分析及测点布置优化研究*
谭仕发,缪炳荣,李 伟
(西南交通大学 牵引动力国家重点实验室,四川成都610031)
高速列车比例车体谐响应分析及测点布置优化研究*
谭仕发,缪炳荣,李 伟
(西南交通大学牵引动力国家重点实验室,四川成都610031)
针对1∶8比例车体振动测试试验中的测点布置问题,建立比例车体有限元模型,在其底部二系弹簧对应点施加简谐荷载以模拟激振力,采用模态叠加法进行谐响应分析,得出关键点在激振力作用下的位移变形情况。对比分析结果,得出危险变形位置,并以此进行测点布置优化。研究结果表明,比例车体2/7、3/7截面上的测点对车体垂向激励有很好的响应信号,适合布置测点,为比例车体模态测试分析提供一定的理论参考。
比例车体;谐响应分析;布置优化
高速铁路快速发展形式,对机车牵引效率及列车轻量化提出了高要求,同时,为保证列车运行安全,车辆动态特性的研究变得尤为重要。但是进行整车结构线路动应力试验和振动测试费用非常高昂,而利用比例车体可以更好地研究车体结构的不同截面尺寸以及不同质量、材质和结构强度、刚度等设计参数下的车辆减振特性[1]。C.Bilik等应用1∶10比例车体研究了抑制结构振动的不同方法[2]。Joel H ansson等利用新干线列车1∶5比例车体进行研究,提出了抑制车体振动,提高乘坐舒适度的一种新方法[3]。
在谐响应分析方法应用方面,苏勋文等应用谐响应分析方法,对中减速器机匣施加激励信号,根据各关键位置点对激励信号的响应振幅来优化传感器的安装位置[4]。张宪等基于疲劳振动试验台,应用谐响应分析方法研究不同载荷位置对试验台系统位移响应的影响[5]。孙建国等在对车体局部模态分析的基础上,应用谐响应方法,对比分析了变压器在两种安装位置上的响应位移[6]。针对1∶8比例车体振动测试试验中的测点布置问题,提出应用谐响应分析方法,根据关键点响应位移,初步设定测点位置。
1 理论背景
谐响应分析用于确定线性结构在简谐荷载作用下的稳态响应,得出结构在各激振频率下的位移响应,即幅频关系。对于多自由度系统动力学方程为[7]

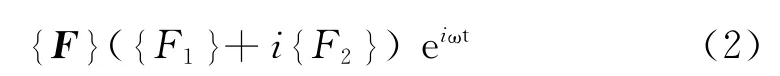

根据谐响应分析特点,激励力是简谐力,故系统的稳态振动也是简谐振动,令


为将物理坐标下的动力学方程式(1)解耦,需将运动方程应用模态坐标系表示,模态坐标系下,动力学一般方程为
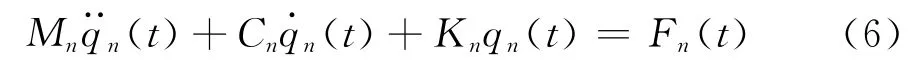
式中Mn、Cn、Kn、qn(t)、Fn(t)分别为第n阶模态对应的主质量、主阻尼、主刚度、主坐标和激振力。令可表示为阻尼系数Cn=2Mnωnξn,主刚度则式(6)表示为
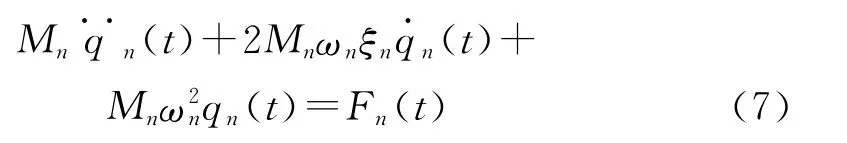
模态坐标系下,初始位移和初始速度可表示为
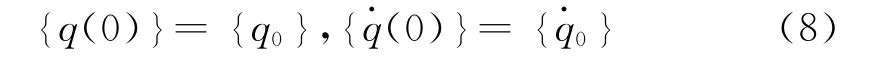
在稳态简谐振动时,模态位移和模态激励可分别表示为
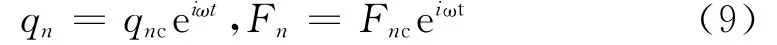
式中n=1,2,…,;qnc、Fnc分别为第n 阶模态下的响应幅值和激励幅值。将式(9)代入式(7),整理得
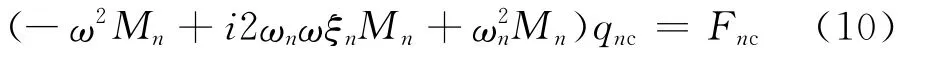
则模态坐标系下响应幅值
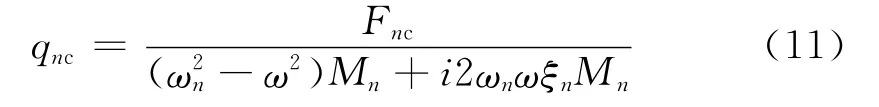
因此,第n阶模态对应的稳态位移响应为


若考虑结构初始条件,
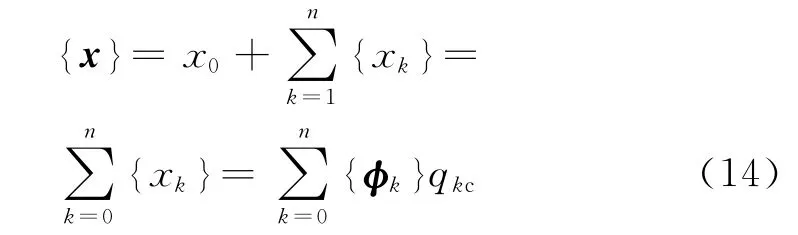
2 研究内容
2.1比例车体有限元模型的建立
根据比例车体实际尺寸3 022 m m×407 m m×350 m m,模型由铝板焊接而成,铝板厚度4 m m,简化非重点研究局部的小圆角,采用Solid w orks软件建立比例车体三维模型图,并导入H yper M esh软件抽取中面划分网格。网格单元采用四节点Shell63,模型材料弹性模量为7.0×1010Pa,泊松比选用0.3,密度采用2.7× 103kg/m3。比例车体有限元模型示意如图1,在长度方向上将模型6等分,关键点设置如图2,点23为比例车体模型底部中点,箭头表示激振点位置、激振力方向,弹簧为模型约束示意。
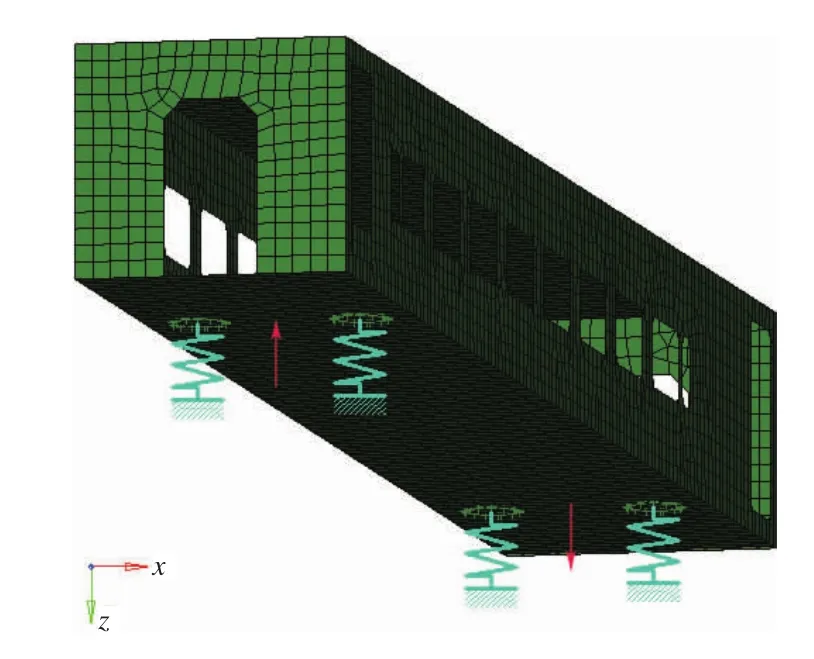
图1 比例车体有限元模型示意图
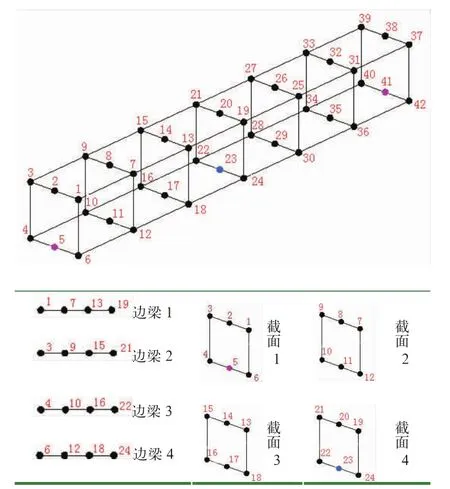
图2 比例车体关键点的设置示意
2.2模型验证
(1)试验模态分析
模态分析作为结构动力学逆问题分析方法的一种,是研究结构动态特性的一项综合性技术,广泛应用于航空、航天、桥梁、建筑、交通运输等工程领域。模态试验的主要目的在于辨识系统特性参数、预判结构易损伤局部、探究系统各部件间振动传递率等,另外,模态试验的结果可用于验证和修正结构系统的数学模型,鉴定结构动态特性是否满足设计要求。本文在研究工作中对比例车体进行了模态试验,限于篇幅,试验结果以图3简单示出。lng表示响应加速度与激励力之比。

图3 比例车体Z方向测试频响函数图
(2)有限元模态分析
有限元模态分析是模态分析技术与有限元仿真技术的结合,与试验模态分析相比,前者不仅能灵活地改变结构几何参数并提出优化方案,同时,在产品设计过程中,不能用试验的方法来判定结构的动态特性,有限元模态分析技术的应用可缩短产品研发周期、降低生产成本。本文采用缺省Block Lanczo法提取比例车体前十阶模态,计算所得固有频率及振型如图4。
为保证仿真关键点与现实测点对应关系的准确性,必须保证所建模型的正确性,论文提取模态分析前10阶计算结果与模态试验结果进行对比[8-10],如表1。

图4 比例车体前10阶模态

图5 边梁1上各点负Z方向变形位移

表1 计算模态与试验模态结果对比
由表1可以看出,所建比例车体前10阶计算模态频率与试验模态频率最大误差为2.69%,表明所建模型与实际相符度高,满足本文的基础研究建模要求。另外,此处的模态分析为下文谐响应分析的模态叠加计算保留了结果文件。
2.3谐响应分析
当谐响应分析中模态叠加频率为最大模态计算频率的1.5倍时,获取的响应结果更准确[11-12]。载荷的加载具有两种形式,一种是实部虚部形式,另一种是幅值与相角形式,选用实部虚部的形式施加简谐荷载。根据车体模态试验经验,在比例车体底部二系弹簧对应点施加负Z向的反相荷载以模拟激振力,载荷幅值为1 k N;根据模态分析结果,设定载荷频率段为0~350 H z,频率增量为1 H z;应用谐响应分析中的模态叠加法,计算结果模态叠加范围为7~50阶;计算结果用贝塞尔曲线(Bezier curve)拟合。根据几何模型及作用载荷的对称性,选择1/2比例车体4条边梁、4个截面(图2)上的关键点Z方向变形位移作对比分析。

图6 边梁2上各点负Z方向变形位移
从变形位移图(图5~图8),可以看出4条边梁上各对应点位移变化规律具有很高的相似性:在载荷频率处于95~155 H z段时,各边梁上关键点共振位移峰值均出现4次,峰值点频率分别为99,113,130,152 H z,各峰值频率处,关键点位移随所在截面与激励点距离的增大,幅值有减小趋势,如图3所示,频率为113 H z时,截面1中关键点1大于截面2中的关键点7的位移,而截面1正是激振点所在截面;当载荷频率处于210 H z附近时,4条边梁中间两关键点位移出现最大峰值;其他频率范围振动位移不明显。为了清楚直观地展现最大峰值处各关键点的变形位移,提取激振力频率为210 H z时各边梁响应位移数值进行对比,如表2。
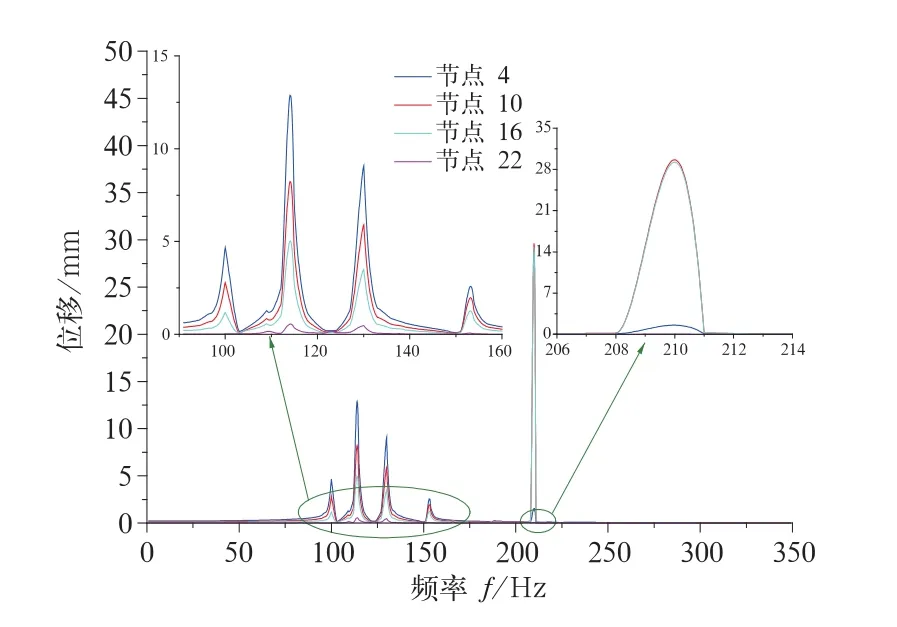
图7 边梁3上各点负Z方向变形位移
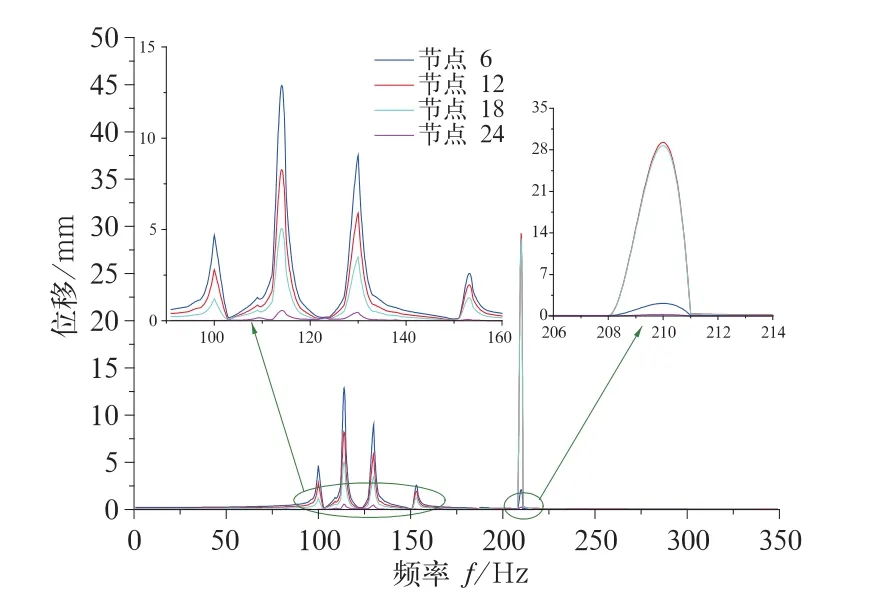
图8 边梁4上各点负Z方向变形位移
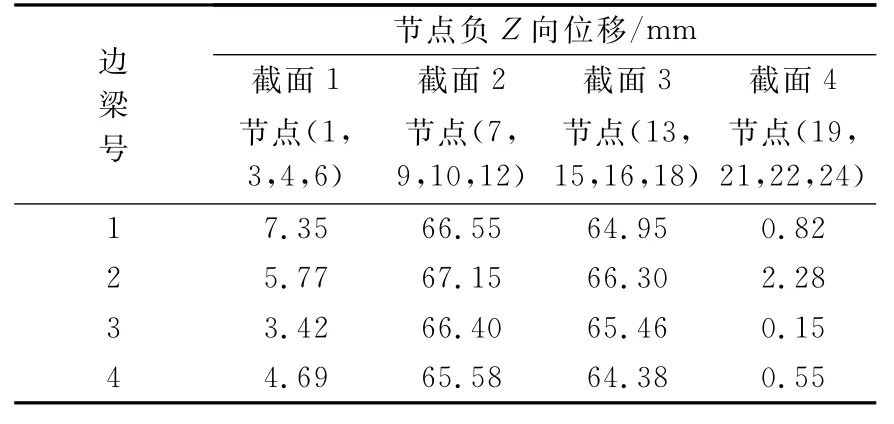
表2 210 Hz激振力作用下各边梁对应关键点位移
对比分析表2数据:激振力为210 H z时,截面内各点的变形位移相差较小,如截面4中节点19、21、22、24变形位移分别为0.82、2.28、0.15、0.55,表明比例车体在负Z方向上局部变形较小;截面2、3上的各点变形位移与1、4两截面上各点相比,位移变形相差较大,相同条件下,前者更易产生裂纹;4条边梁上关键点位移变化趋势一致(表2横向对比),且位移幅值相近。
3 结论与展望
建立了高速列车比例车体有限元离散模型,以Z方向的反相简谐荷载作用于比例车体底部二系弹簧对应点,进行了谐响应分析,获取1/2比例车体4条边梁上各关键点的位移响应曲线,得出了比例车体上部分节点的位移响应规律。该研究工作主要针对比例车体结构的振动测试研究中的测点布置优化展开研究,为车体的单点/多点激励,变换激励点的位置、施加不同载荷、改变比例车体支撑或悬挂方式、车外吊挂等条件,进行试验研究和仿真分析提供技术支持。具体的研究结论如下:
(1)当激振力频率段为95~155 H z时,Z向位移出现4个位移幅值,其中最大峰值处于113.6 H z,节点1获得最大位移12.78 m m。那么节点1应选作测点,另外节点1处Z方向传感器在95~155 H z频率段应有较好的传输特性,特别是由于95~155 H z范围内峰值出现频繁,测点所布置传感器应有较高的灵敏度。
(2)当激振力频率为210 H z时,截面2(节点7、9、10、12)以及截面3(节点13、15、16、18)出现较大位移响应,各点均值为28.67 m m,由于振动频率较高,振动幅值大,同等情况下更易产生疲劳裂纹,截面2、截面3附近应多布置测点,同时,为避免测试信号的失真,Z向传感器应选用较大量程。
(3)激振力处于其他频率段时,各关键点位移响应幅值不明显,可选择性布置测点。根据模型及激励力的对称性,另外1/2比例车体测点布置可按此方法同样处理。
(4)研究方法对于旋转机械,或受周期载荷激励的结构,应用谐响应分析的方法对测点布置,都有一定的可行性。
[1] 张 盈,缪炳荣,等.多目标比例车体振动试验台的结构设计[J].铁道机车车辆,2013,33(5):6-8.
[2] C.Bilik,et al.A PC-based m ulti purpose test bed environ ment for structural testing and control[C].Proceedings of theR E V2006 conference,M aribor,Slovenia,2006,(6):29-30.
[3] Joel H ansson,et al.Vibration Suppression of Railway Car Body With Piezoelectric[J].Journal of A dvanced M echanical Design systems and M anufacturing,2007,1(5):649-658.
[4] 苏勋文,王少萍,等.直升机中减速器谐响应分析与传感器优化布局[J].北京航空航天大学学报,2011,37(9):1049-1052.
[5] 张 宪,何 洋,等.疲劳振动试验台的模态与谐响应分析[J].机械设计与制造,2008,(4):13-14.
[6] 孙建国,苏永章.车体地板局部模态与谐响应分析[J].电力机车与城轨车辆,2012,35(5):56-58.
[7] 非周期激励作用下振动系统的谐响应分析[J].机械强度,2010,32(6):878-883.
[8] 付长虎,刘红光,等.客车车身的有限元模态及谐响应分析[J].重庆交通大学学报(自然科学版),2013,32(6):1267-1269.
[9] 梅 翔,缪炳荣,等.高速卧铺列车计算模态与实验模态的对比研究[J].机械制造,2013,51(590):63-65.
[10] 张 盈.比例车体实验台的模态参数识别研究[D].四川:西南交通大学,2013:1-75.
[11] Luo Y un,Feng Guoying,et al.The Dynamic Response A nalysis of A uto Body Sheets to Node Loads[J].Int. Journal of Engineering Research and A pplications,2014,4(1):201-205.
[12] W.S.Rathod and K halid A nsari.M odal and H arm onic analysis ofTurbocharger turbineusingFiniteElement M ethod[J].International Journal of A pplication or Innovation in Engineering&M anagement,2013,2(7):6-9.
Harmonic Response Analysis of the Scaled Car-body of High Speed Train and Configuration Optimization of M easuring Points
T A N Shifa,M IA O Bingrong,LI W ei
(State Key Laboratory of Traction Power,South west Jiaotong U niversity,Chengdu 610031 Sichuan,China)
For the measuring pointlayout problem of the 1:8 scaled car-body presented during stress and strain test experiment,the paper established finite element m odel of the scaled car-body,and applied harm onic load to sim ulate the excitation force at two points ofits botto m.H arm onic response is analyzed using m odal superposition method,and deformation displacement of the key point is obtained under the exciting force.Co m paring the analysis result and obtain the dangerous deformation position,the optimization can be done. The research results show that,the response signal of measuring point on the 2/7 and 3/7 section of the scaled car-body are very good,suitable for arrangement of measuring points.The results provide a certain reference for m odeltest and analysis of the scaled car-body.
scaled car-body;harm onic response analysis;configuration optimization
U260.11+1
A
10.3969/j.issn.1008-7842.2015.05.02
1008-7842(2015)05-0005-04
专题研究
*国家自然科学基金面上项目(51375405);四川省应用基础研究计划项目(2012JY0094)
谭仕发(1989—)男,硕士研究生(2015-03-25)

