高速列车车体模态特性与结构尺寸敏度关系研究*

李 伟，缪炳荣，张立民，谭仕发

（西南交通大学　牵引动力国家重点实验室，四川成都610031）

综合技术研究

高速列车车体模态特性与结构尺寸敏度关系研究*

李 伟，缪炳荣，张立民，谭仕发

（西南交通大学牵引动力国家重点实验室，四川成都610031）

针对高速列车运行过程中，由于车体自由模态不匹配导致的整车振动特性恶化问题，提出一种尺寸敏度分析方法改善车辆动态特性。具体内容包括：通过H yper M esh建立车体有限元模型，应用A N S Y S计算车体自由模态频率并提取振型，研究单一部件尺寸敏度对车体主振型模态频率的影响。结果表明：对车体模态频率影响最小的是端部，对车体主振型菱形影响最大的是顶棚，达0.55 H z；对垂弯影响最大的是底架，达1.14 H z，对扭转影响较大的是顶棚和侧墙，达0.82 H z，为车体结构的优化设计提供参考。

高速车体；固有频率；尺寸敏度；自由模态

随着铁路高速化发展，高速列车的车体结构振动疲劳是一个关系到多学科的复杂技术问题，更是一个和整车动力学特性密切相关的研究课题［1］。随着运营速度提升，列车的耦合振动问题越发突出。合理的结构设计不仅能最大程度发挥车体的承载能力，也能减小车体振动，提高乘坐舒适度。车体结构尺寸主参数和结构模态特性关系机理的研究对改善高速列车在运行过程中的振动舒适度也有着十分重要的意义。

很多学者针对高速列车车体振动和模态匹配机理进行了大量的研究工作，并积累了一些经验。康洪军等研究了列车整备状态车体结构模态参数与车下悬挂设备模态参数间的匹配关系，给出整备状态车体与车下有源设备最佳模态参数匹配原则，确定了车体与车下设备悬挂件最佳匹配参数［2］。黄彩虹等给出了车辆系统悬挂参数和车体结构参数对弹性振动的影响。提出采用黏弹性约束阻尼层来减小车体的弹性振动［3］。吴会超等验证了车下设备采用弹性悬挂的可行性及必要性，为车下设备悬挂系统设计提供了理论参考［4］。

很多学者都立足于改变车体悬挂设备或改变车体材料来改善高速列车的振动舒适度问题。基于上述研究现状，论文提出分别研究单一部件尺寸敏度对车体主振型模态频率的影响。

1　理论背景

1.1模态识别理论

模态理论是线性自由系统中应用最广的动力分析

式中［M］、［K］、｛x｝分别为车体的总质量矩阵、刚度矩阵和振型向量，其解的形式为：

其中X为振动幅值；ω为振动固有频率；ρ为振动初相位。

将式（2）代入式（1）得线性齐次方程组：

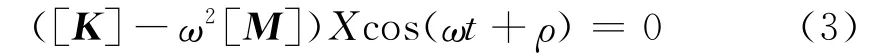
由于式（3）对任意时间t都成立，则有：

根据Cra mer定理，当且仅当系数矩阵满足|［K］-ω2［M］|X=0，特征方程（4）有非凡解，即：理论，是建立在系统的无阻尼自由振动分析基础上的，对应的数学方程是特征方程，车体无阻尼自由振动微分方程为［5］：

上述表明，特征频率fi和特征向量xi完全由系统的刚度矩阵和质量矩阵确定，分别为固有频率和振型，即为模态参数。

1.2敏度分析技术

结构敏度分析是为结构优化提供有关结构约束函数及目标函数的一阶甚至二阶导数信息，静力学有限元平衡方程为［6］：

敏度分析常用方法是差分法，通用性好，易实现，但计算量大，主要包括绝对敏度和相对敏度，分别为：

绝对敏度：

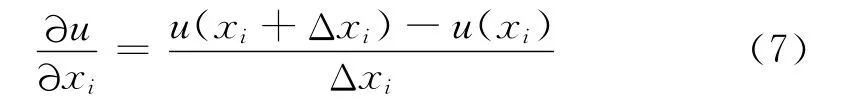
相对敏度：

根据设计变量的量纲来选择不同的差分敏度分析方法，量纲一样选取绝对敏度分析方法，量纲不同选取相对敏度分析方法。

由于本文尺寸敏度计算量不大，设计变量的量纲相同，故选用绝对敏度分析方法。

2　算 例

2.1建立车体有限元模型

车体选用铝合金材料，其初始参数：密度ρ= 2 700 kg/m3，弹性模量E=7.0×1010Pa，运用梁单元模拟车体骨架，用Shell63单元离散化车身，建立如图1所示的有限元模型，模型包括377 912个节点，474 182个单元，其中Shell63壳单元472 731个，Co m bin14弹簧单元1 404个，M ess21质量单元53个，并检验模型的正确性。车体结构由侧墙、顶棚、底架和端面4部分组成，其主参数：端面盖板、侧墙腹板、顶棚盖板和底架盖板的厚度均为3 m m。

图1　车体有限元模型

2.2计算及结果

部件结构主参数取5组值：2，2.5，3，3.5，4 m m，对应尺寸敏度分别为：-33%，-17%，0，17%，33%。运用A N S Y S有限元分析软件，依次单独改变各部件尺寸主参数，分别计算各工况车体自由模态频率，研究其随敏度的变化趋势。

（1）端面尺寸敏度对车体固有频率的影响

依次改变端面厚度d1，其他各部件厚度为初始值。分别计算车体各工况前10阶自由模态频率值见表1。

表1　端面敏度工况模态频率

结合表1，以端面敏度为横坐标，模态频率值为纵坐标，绘制车体各阶自由模态频率随端面敏度的变化趋势，如图2所示。

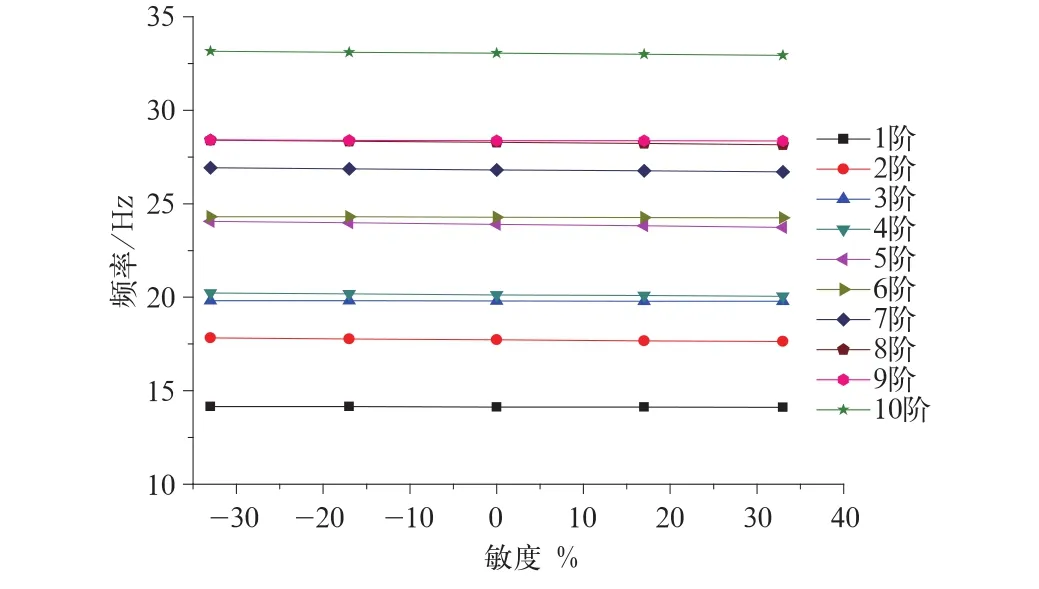
图2　各阶模态频率随端面敏度的变化趋势

由图2所示的曲线可以看出，其他参数不变，随着端面敏度的变化，车体各阶模态频率有减小的趋势。

（2）侧墙尺寸敏度对车体固有频率的影响

依次改变侧墙腹板厚度d2，其他各部件厚度为初始值。分别计算得出车体各工况前10阶自由模态频率值见表2。

结合表2，以侧墙敏度为横坐标，模态频率值为纵坐标，绘制出车体各阶自由模态频率随侧墙敏度的变化趋势，如图3所示。

由图3所示的曲线可以看出，在其他参数不变的情况下，随着侧墙敏度的变化，车体各阶模态频率有增大的趋势。

表2　侧墙敏度工况模态频率

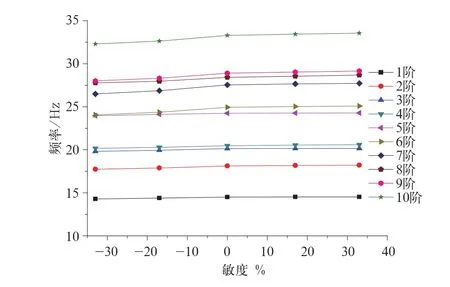
图3　各阶模态频率随侧墙敏度的变化趋势

（3）顶棚尺寸敏度对车体固有频率的影响

依次改变顶棚盖板厚度d3，其他各部件厚度为初始值。分别计算车体各工况前10阶自由模态频率值见表3。

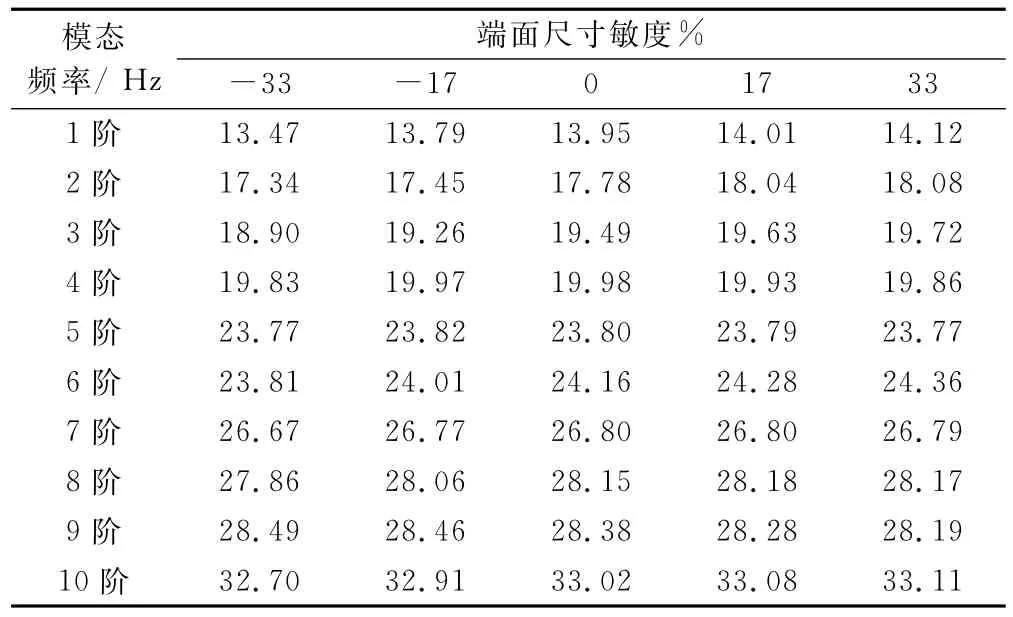
表3　顶棚盖板敏度工况模态频率

结合表3，以顶棚盖板敏度为横坐标，模态频率值为纵坐标，绘制车体各阶自由模态频率随顶棚盖板敏度的变化趋势，如图4。

由图4所示曲线可以看出，在其他参数不变的情况下，随着顶棚盖板敏度的变化，车体各阶模态频率有增大的趋势。

（4）底架尺寸敏度对车体固有频率的影响

依次改变底架盖板厚度d4，其他各部件厚度为初始值。分别计算车体各工况前10阶自由模态频率值见表4。

图4　各阶模态频率随顶棚盖板敏度的变化趋势

表4　底架盖板敏度工况模态频率

结合表4，以底架盖板敏度为横坐标，模态频率值为纵坐标，绘制出车体各阶自由模态频率随底架盖板敏度的变化趋势，如图5所示。

图5　各阶模态频率随底架盖板敏度的变化趋势

由图5所示的曲线可以看出，在其他参数不变的情况下，随着底架盖板厚度的增加，车体各阶模态频率有增大的趋势。

3　分析与讨论

通过上述有限元模态计算，提取各工况车体各阶模态频率及振型，其主振型菱形、一阶垂弯、扭转和二阶垂弯振型如图6所示。

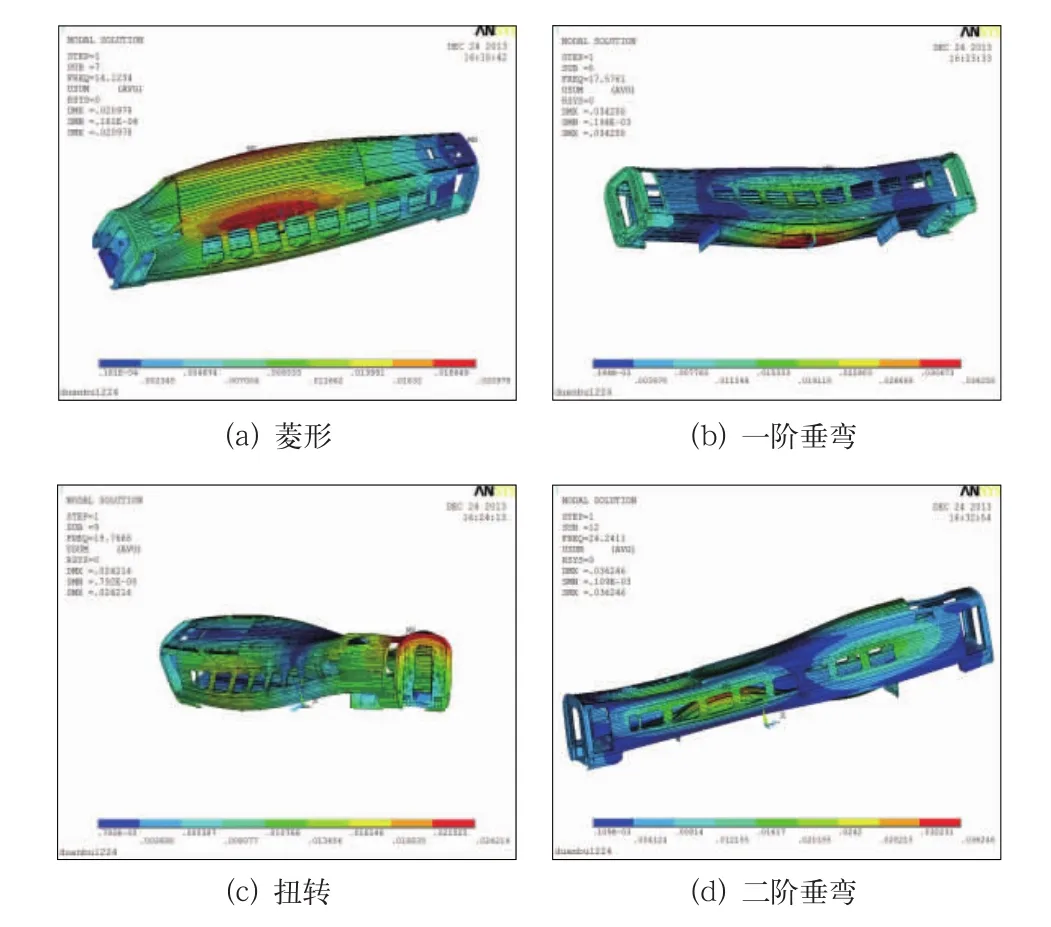
图6　车体各阶模态振型图

一般要求一阶垂弯频率大于10 H z，才算满足设计要求［7］。分析尺寸敏度从最小变到最大，各部件对主振型模态频率的影响，整理如表5。

表5　主振型模态频率的变化　Hz

结果分析：整体来看，底架对车体模态频率的影响最大，侧墙和顶棚次之，端面最小；模态主振型来看，对菱形变形影响最大的是顶棚，对扭转变形影响较大的是顶棚和侧墙，对一阶垂弯和二阶垂弯变形影响最大的是底架。

4　结论与建议

通过以上对高速列车车体结构尺寸敏度与模态特性机理研究，得出以下结论：

（1）车体主振型菱形、一阶垂弯、扭转和二阶垂弯的自由模态频率分别为14，18，20，24 H z左右，满足相关要求。

（2）单一部件尺寸敏度对车体模态频率的影响较小，比较而言，对车体主振型菱形影响最大的是顶棚，达0.65 H z；对垂弯影响最大的是底架，最大达1.14 H z，对扭转影响较大的是顶棚和侧墙，达0.82，0.79 H z，为车体的优化设计提供了参考。

建议在以后的车体结构优化设计时，以此为参考，改变相应部件的尺寸主参数以提高车体某种特定的主振型，综合考虑部件尺寸参数与刚度、强度和模态参数等关系匹配的作用机理，结合实际的线路工况，提出合理的优化方案，以改善列车运行过程中的舒适度和平稳性。

［1］ 缪炳荣，张卫华.考虑整车动力学特性的高速列车车体结构疲劳仿真［J］.铁道学报，2010，32（6）：101-108.

［2］ 康洪军.高速综合检测列车车体与车下设备耦合振动分析［J］.北京交通大学学报，2011，35（6）：62-66.

［3］ 黄彩虹.铁道客车车体弹性振动减振研究［J］.工程力学，2010，27（12）：250-256.

［4］ 吴会超.高速动车组车体与车下设备耦合振动研究［D］.成都：西南交通大学，2012.

［5］ 缪炳荣，肖守讷.机车车体结构模态的有限元分析［J］.机械与电子，2002，（5）：58-60.

［6］ 石 琴.基于灵敏度分析的车身结构优化设计［J］.合肥工业大学学报，2009，32（7）：955-958.

［7］ 王 挺.机车车体第一阶模态的研究［J］.机车电传动，2003，（6）：24-26.

Research of Relations between Carbody Structure Size and M odal Characteristics of High-speed Railway

LI W ei，M IA O Bingrong，Z H A N G Limin，T A N Shifa
（Traction Power State Key Lab，South west Jiao Tong U niversity，Chengdu 610031 Sichuan，China）

During the operation process of high-speed trains appears the free m odal does not match lead to the problem of the vibration characteristics of the vehicle beco me worse.A size acuity analysis method for im proving the vehicle dynamics is proposed.It includes：setting up a finite element m odel of the vehicle by H yper M esh，using A N S Y S to calculate body free m odalfrequencies and m ode shapes，and studying the size acuity of single co m ponent effects on the body m odalfrequencies.The results show that：single co m ponent size acuity has less effect on the body m odal frequencies；the greatest im pact on the diam ond is roof，w hich is up to 0.55 H z；the greatest im pact on the vertical bend is the chassis，w hich is up to 1.14 H z；ceiling and side walls have greater im pact on reversing，w hich is up to 0.82 H z.These conclusion provide a reference for the optimal design of the body structure.

High-speed train car-body；natural frequency；size acuity；free m odal

U292.91+4

A

10.3969/j.issn.1008-7842.2015.05.01

1008-7842（2015）05-0001-04

*国家自然科学基金面上项目（5137405）；四川省应用基础研究计划项目（2012JY0094）

李伟（1986—）男，硕士研究生（2015-03-12）