基于经验模态分解及时域积分的轨道高低不平顺获得方法
陈道云,孙守光,李 强
(北京交通大学 机械与电子控制工程学院,北京100044)
基于经验模态分解及时域积分的轨道高低不平顺获得方法
陈道云,孙守光,李 强
(北京交通大学机械与电子控制工程学院,北京100044)
分析了信号中的趋势项产生原因,并推导了时域积分过程中趋势项的产生过程;利用经验模态分解的方法提取并去除了实测列车轴箱垂向加速度信号的趋势项,然后对去趋势项的加速度信号在时域内连续两次积分得到轨道高低不平顺数据;分别用经验模态分解法和最小二乘法去除了积分过程中产生的趋势项,并将两种方法的处理结果进行了对比分析。分析结果表明,利用最小二乘法去除信号及积分过程中产生的趋势项存在较大的计算误差,而利用经验模态分解的方法则可以有效去除信号及积分过程产生的趋势项,从而得到轨道高低不平顺数据。
加速度;经验模态分解;最小二乘法原理;趋势项;时域积分;轨道高低不平顺
轨道不平顺对机车车辆系统是一种外部激扰,是产生机车车辆系统振动的主要根源。按其对车辆激扰作用的方向可分为垂向轨道不平顺和横向轨道不平顺。左右轨垂向、横向不平顺又可组合成常说的高低、水平、轨向及轨距4种不平顺。
目前轨道不平顺的获取主要依靠轨检车,系统很复杂。为了简单地获得轨道不平顺数据,本文采用了一种基于经验模态分解及时域内轴箱加速度积分的方法,该方法易于实现且精度较高,比较适合对轨道进行简易评估。
对于加速度信号的积分,之前有大量的科研工作者对其进行了不同形式的研究,而对于趋势项的消除方法,普遍采用的是最小二乘法原理[1-2],这种方法对处理平稳且数据量小的信号具有很大的优势。对于本文中研究的非平稳随机的加速度信号,采用这种方法得到的结果往往是不准确的。为此,本文利用经验模态分解技术对加速度信号及时域积分产生的趋势项进行了去除,得到了轨道高低不平顺数据。
1 趋势项
1.1信号本身的趋势项
实际采集的加速度振动信号,由于放大器随着温度变化产生的零点漂移、传感器频率范围外低频性能的不稳定以及传感器周围的环境干扰,往往会偏离基线,甚至偏离基线的大小还会随着时间变化。偏离基线随时间变化的过程称为信号的趋势项,它的存在会直接影响到信号的正确性,因此必须将其去除。
1.2时域积分及其趋势项
在时域内对轴箱加速度信号两次积分是获得轨道高低不平顺的最直接方法。数值积分的方法有很多,如梯形公式、Sim pson公式、Newton-Cotes公式、复化梯形公式、复化Sim pson公式等[3]。为了提高积分的精度且方便运算,本文采用复化Sim pson公式对加速度信号进行两次积分,分别得到速度信号和位移信号:
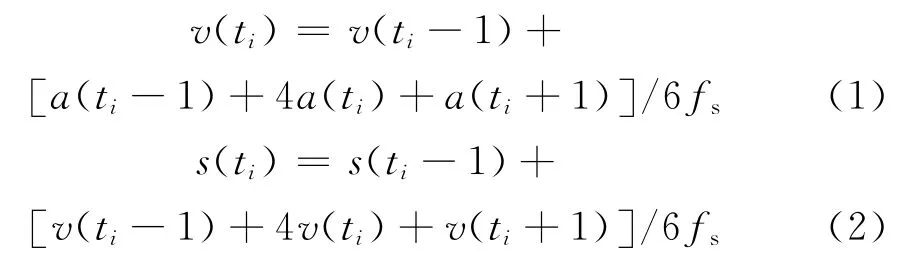
式中

然而,直接通过时域积分的方法获得的轨道高低不平顺数据是不准确的,这种偏差的原因正是由于趋势项的存在。
假设加速度信号中含有微小直流分量,即

一次积分得:

二次积分得:
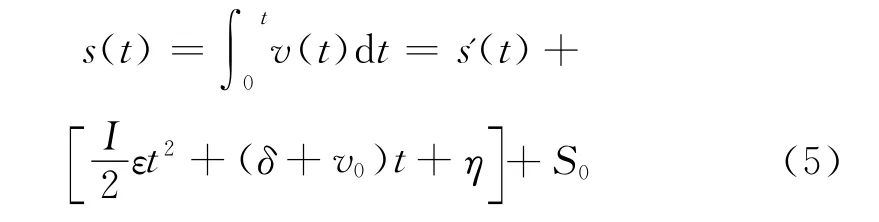
式中δ,η分别为ε一次、二次积分后产生的积分常量。
由式(3)~式(5)可以看出,在一次、二次积分后分别产生了一次、二次趋势项,因此应予以去除。
1.3趋势项的去除
(1)基于经验模态分解的趋势项去除
1998年美国宇航局的N orden E H uang等[4]提出了一种新的信号处理方法,该方法主要由两部分组成:首先采用经验模态分解(E m pirical M ode Deco m position,以下简称E M D)将原始时间信号分解成一组本征模函数(Intrinsic M ode Function,以下简称I M F),然后再对每一个I M F进行Hilbert变换。
本文利用其中的E M D方法提取并去除信号中的趋势项。算法如下:
(1)找出信号x(t)的所有极大点和极小点,用3次样条曲线分别拟合为原数据序列的上包络线U(t)和下包络线L(t),上、下包络线的均值

将原数据序列x(t)减去m1(t)可得到一个去掉低频的新数据序列h1(t),其式为

判断h1(t)是否为I M F的条件有两个:
①对于一列数据,极值点和过零点数目必须相等或至多相差一点;
②在任意点,由局部极大点和极小点构成的两条包络线的平均值为零。
如果h1(t)不满足上述条件,那么将h1(t)看成,则
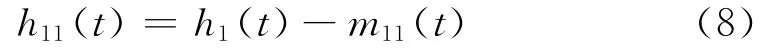
重复以上过程m次,直到所得的h1m(t)满足I M F所必需的条件,此时h1m(t)就是第一个I M F,记为I M F1(t),它表示信号中的最高频成分。
(2)用x(t)减去I M F1(t)得到一个去掉高频成分的新数据序列r1(t),其式为

将r1(t)看作是原数据序列重复步骤(1),可得到一系列I M Fi(t)和最后一个不可分解的序列rn(t)。由此,原数据序列x(t)可表示为一组I M F分量和一个残余分量的和:
E M D分解的收敛特性表明,分解得到的残余信号分量rn(t)为单调函数,其中包含了测试信号中频率最低的成分,其周期大于采样信号的长度,所以rn(t)即为测试信号中包含的趋势项[5]。
(2)基于最小二乘法原理的趋势项去除
信号测试的采样频率记为fs,总采样时间记为T,则采样时间间隔Δt=1/fs,实测的加速度信号记为a(ti),其中:
构造一个多项式函数

其中Pk为多项式系数;φ为所有次数不超过n(N≤T/ Δt-1)的多项式构成的函数类,使得函数λn(ti)与离散数据a(ti)的误差平方和最小,即:

若想确定拟合趋势项,只需确定某一组Pk的值,使得E最小。由多元函数求极值的必要条件:

其中,j=0,1,2,…,n因而可以得到:

用矩阵表示为
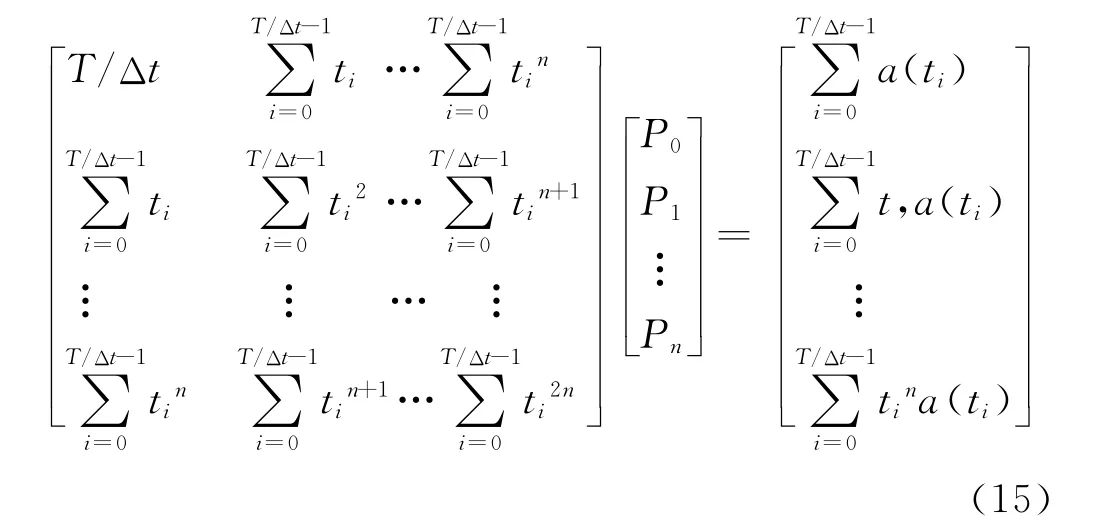
可以证明,方程组的系数矩阵是一个对称正定矩阵,故存在惟一解。
2 加速度信号测试及去除趋势项处理
2.1测试情况
2014年11月12日对尚未开通的沪昆高铁线路上运行的CRH3 A型动车组的轴箱垂向加速度等参数进行了线路实测,测试区间为南昌西至玉山南。

图1 CRH3 A型动车组
测试选用IC压电式单向加速度传感器,其灵敏度为25.1 m V/g,频率范围为0.7~11 000 Hz,量程为100g,布置在1-2L号轴箱与一系减振器之间。采用德国IM C数据采集系统对加速度信号进行采集,如图2所示。
2.2加速度信号去除趋势项
在车辆运行平稳的区段,截取1 s时长的加速度测试数据,观察加速度值随时间的变化情况,如图3所示。

图2 加速度传感器安装位置及数据采集系统

图3 含有趋势项的加速度信号
现有的消除趋势项的方法大多需要预先假定信号中趋势项的类型,这就需要对测试信号中包含趋势项的特征具有一定的预先验证知识,因而不适用于处理随机信号。
本文利用E M D算法,通过M atlab编程对上述加速度信号进行分解,所得的I M F及其对应的功率谱(PSD)分析如图4所示。
对图4进行分析可以发现:
(1)轴箱加速度信号被成功分解为I M F1~I M F10及Trend共11个分量。I M F1频率最高,波长最短,在随后的分量中,频率逐渐变低,波长变长,其中Trend的频率最低。各个I M F分别以不同的分辨率体现了信号中该频段范围内的振动模态。
(2)轴箱加速度信号的频谱比较丰富,大部分信号分量集中在1 000 H z以下。I M F1~I M F6属于测试信号的优势频段,体现了轴箱垂向振动的主要时频特征。I M F7~I M F10属于测试信号中包含的低频成分。余量Trend频率很低且所占能量很大,其为单调函数,周期大于采样信号的长度,因此属于低频趋势项,须将其去除。
3 轨道高低不平顺数据的获取
在时域内,对去除趋势项的轴箱加速度信号连续两次积分便得到轨道的高低不平顺,如图5所示。
可见时域内积分获得的位移激扰含有明显的趋势项,这是因为在去除了加速度信号的趋势项之后,新的加速度信号中不可避免地残留有微小的直流分量,在积分过程中,这种微小的直流分量被逐渐放大,以至于偏离正确值,因而需对其进行去除趋势项的处理。现分别利用E M D方法和最小二乘法,编写M atlab程序对积分得到的位移信号去除趋势项。
3.1E M D方法去除积分趋势项
利用E M D原理编写M atlab程序对上述位移信号进行分解,所得的I M F 分量及其对应的功率谱(PSD)分析如图6所示。
对图6进行分析,发现经E M D分解得到的4个分量中,Trend的频率最低且所占能量较大,其为单调函数,周期大于采样信号的长度,因此为趋势项,须将其去除。去除趋势项后的位移信号如图7所示。
3.2最小二乘法去除积分趋势项
利用前面提到的最小二乘法也可以去除由时域积分产生的趋势项,去除趋势项后的位移数据如图8所示。
3.3两种去除趋势项方法的对比
首先将E M D得到的趋势项和最小二乘法拟合的二次趋势项进行对比,如图9所示。
可以看出,两条拟合趋势曲线的大致走向是一致的,相比最小二乘法拟合趋势项,E M D分解得到的趋势项波动更明显一些,这与E M D分解的本质特征有关,因为这种分解完全依据数据自身的时间尺度特征来进行信号分解,具有自适应特征,因而提取趋势项的精度非常高,而利用最小二乘法拟合的趋势项则是一条标准的二次函数曲线,与E M D相比,精度偏低。
然后将两种方法去除趋势项后得到的位移数据进行对比,如图10所示。
观察图10可以发现,通过最小二乘法去除趋势项得到的位移信号波动幅度要明显大于通过E M D方法去除趋势项得到的位移信号,但是二者的波形走势却基本相同。导致前者波动幅度大的原因是利用最小二乘法原理去除趋势项本身存在一定缺陷。

图4 I M F及相应功率谱

图5 含趋势项的位移信号
3.4最小二乘法去除积分趋势项的缺陷
在时域内对积分后的数据去除趋势项时,当截取起点相同而长度不同的几组数据时,会导致在数据相同部分得到的位移修正曲线随着截取数据长度的增加而逐渐发生偏移。这是因为当截取的数据长度不同时,利用最小二乘法得到的拟合多项式系数便会不同,从而导致拟合多项式的值也发生变化。

图6 I M F分量及相应功率谱

图7 EMD去除趋势项得到的位移

图8 最小二乘法原理去除趋势项得到的位移
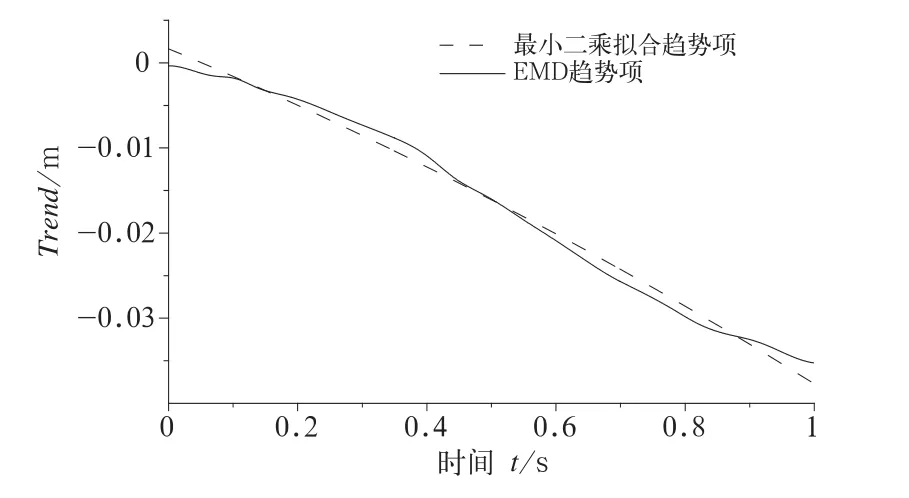
图9 两种方法得到的趋势项对比

图10 两种方法去除趋势项后得到的位移对比
例如若要去除一阶趋势项,则根据式(15)得拟合多项式系数
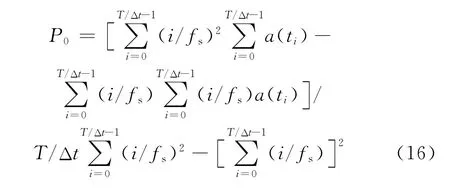

可见,当截取的数据点数不同时,T/Δt的值便会发生变化,因而拟合的一次式系数P0和P1也不同,在起点相同终点不同的各组积分区间内,数据相同部分得到的位移修正曲线便会不同。这也是利用最小二乘法去除趋势项的一个很大的缺陷,这种缺陷正是算法本身的缺陷造成的。
为了用试验数据验证这种积分误差,分别取两个时间区间[0,0.2],[0,1]对加速度数据两次积分并去除二阶趋势项,得到两条位移曲线,为了便于观察,取相同时间区间[0,0.2]作图如图11。
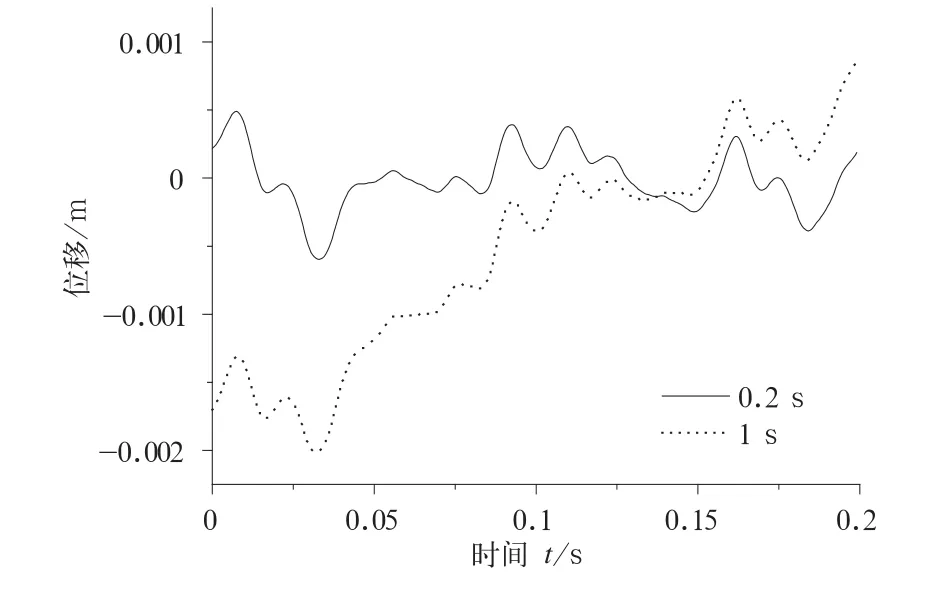
图11 不同长度积分区间对相同时间段积分结果影响
从图中可以看到,随着积分区间长度的增大,在相同区间段[0,0.2]的位移值发生偏移,这正是因为增加了数据点数而导致对前面的拟合带来了影响。为了消除这种影响,可以采用动态递推法[6],步骤如下:
采用某段长度的加速度信号进行积分和拟合修正,将修正位移结果第一个点的值作为最终位移的第一个值,将该段长度的数据点向后递推一个采样点进入下一次循环处理,各次循环处理得到的修正位移的第一个值组成最终位移值。
虽然动态递推法可以有效消除后面数据对前面拟合影响带来的误差,但是该方法的关键在于找到一段积分结果准确的数据区间,这样才能利用动态递推的原理消除因不同数据区间长度而引起的积分结果偏移。对于轴箱加速度信号,如何找到这一个积分结果准确的基准积分区间还有待进一步研究。
4 结 论
(1)趋势项普遍存在于采集得到的信号以及时域积分过程中,运用E M D法可有效地消除实测信号以及时域积分产生的趋势项,使通过轴箱加速度信号积分得到的轨道高低不平顺数据更加准确。
(2)利用最小二乘法在时域内对积分后的数据去除趋势项时,当截取起点相同而长度不同的几组数据时,会导致在相同时间区间部分得到的位移修正曲线随着截取数据长度的增加而逐渐发生偏移。虽然采用动态递推法可以消除这种偏移,但是如何选择合理的基准积分区间有待研究。
[1] 陈为真,汪秉文,胡晓娅.基于时域积分的加速度信号处理[J].华中科技大学学报,2010,38(1):2-4.
[2] 李东文,熊晓燕,李 博.振动加速度信号处理探讨[J].机电工程技术,2008,37(9):50-52.
[3] 王兵团,张作泉,赵平福.数值分析简明教程[M].北京:清华大学出版社,北京交通大学出版社,2012.
[4] H uang N E,Shen Z,Long S R,et al.The e-mpirical mode decomposition and the Hi lbe-rt spectrum for nonl inear and non-stationa-ry time series analysis[J].Proceedings of the Royal Society of London,Series A,1998,454:903-995.
[5] Rilling G,Flandrin P.O n em pirical m ode deco m position and its algorith ms[C]∥Grado.IE E E-E U R A SIPW orkshop on Nonlinear Signal and Image Processing.N SIP-03,June 2003.
[6] 马建仓,刘 琦,程存虎,等.依据振动加速度信号绘制航空发动机转子轴心轨迹的方法[J].航空计算技术,2009,39(4):10-14.
An Acquired M ethod of Track Vertical Profile Irregularity Based on E M D and Time Domain Integral
C H E N D aoyun,S U N Shouguang,LI Qiang
(School of M echanical,Electronic and Control Engineering,Beijing Jiaotong U niversity,Beijing 100044,China)
This paper analyzed the cause of trend item in signals and derived the generation process of trend item in time do main integral. Then it extracted the trend item of actual measured vertical acceleration signals of the axle box and rem oved it.After that,the new acceleration signals were treated by twice-integration in time do main,w hich finally turned into track vertical profile irregularity data.This paper rem oved the trend item produced in the process of time do main integral by using E m pirical M ode Deco m position(E M D)and least square principle and contrasted the treatment results of two methods.The results showed that big calculation errors will happen by using least square principle to rem ove trend item in signals and process of time do main integral.H owever,E M D can rem ove trend item effectively and guarantee the accuracy of track vertical profile irregularity data.
acceleration;E M D;least square principle;trend term;time do main integral;track vertical profile irregularity
U26011+1
A
10.3969/j.issn.1008-7842.2015.05.03
1008-7842(2015)05-0009-06
陈道云(1988—)男,博士研究生(2015-04-27)

