M-矩阵逆矩阵的无穷大范数上界的进一步研究

周 平，黄卫华



-矩阵逆矩阵的无穷大范数上界的进一步研究

周 平，黄卫华

(文山学院数学学院，云南文山663000)

根据-矩阵的性质和无穷大范数的定义，得到严格对角占优-矩阵逆矩阵的无穷大范数上界的估计式，并给出-矩阵的最小特征值下界的新估计式. 理论分析和算例表明，文章给出的两个估计式改进了现有文献的估计算法.

-矩阵；对角占优；无穷大范数；最小特征值

1 基本定义和引理

定义2[1-7]若可表示为. 其中是单位矩阵，，是非负实数且，则称为-矩阵. 特别地，当时，称为奇异矩阵；当时，称为非奇异矩阵. 记所有阶非奇异矩阵所组成的集合为.

定义3[1]设的特征值为，令，则叫做的谱；中模最大的，即称为的谱半径.

定义4[3]设，记，称为的最小特征值且.

定义5[4-7]设，且满足条件：1)，；2)； 3)，. 存在非零元素序列，其中，则称为弱链对角占优矩阵.

定义6[5]设，任取，有，则称为-矩阵. 设，非空指标集合，为行数和列数都是的的子矩阵. 令，其中. 例如表示删去的第一行第一列得到的矩阵.

定义7[5-6]设，若，则称为严格对角占优矩阵.

引理1[5]设是´阶弱链对角占优-矩阵，则也是弱链对角占优-矩阵，且存在，，.

引理3[7]设是严格对角占优-矩阵，，则.

引理4[4]设是´阶弱链对角占优-矩阵，，，，则，，，. 其中.

(2)

由式(1)和(2)，得

.

.

，.

同理，根据定义4可得到下面的推论2.

注：由此推论可知，本文定理2改进了文献[6]中定理2的估计式.

.

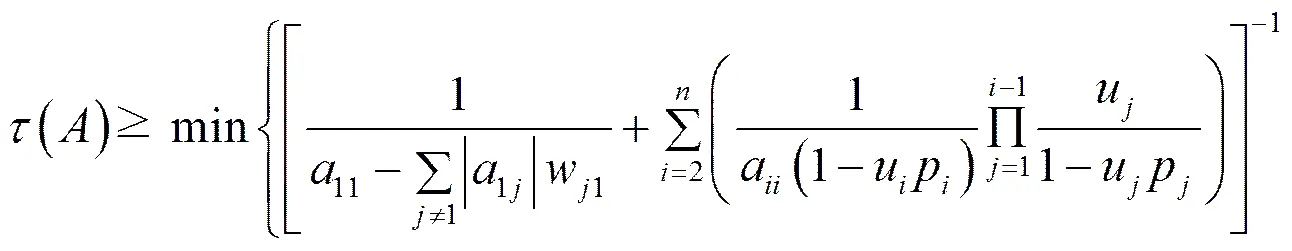
3 算例

[1] 陈景良, 陈向晖. 特殊矩阵[M]. 北京: 清华大学出版社, 2001: 23-87.

[2] VARGA R S. On diagonal dominance arguments for bounding ||-1||¥[J]. Linear Algebra and its applications, 1976, 14(3): 211-217.

[3] CHENG G H, HUANG T Z. An upper bound for ||-1||¥of strictly diagonally dominant M-matrices[J]. Linear Algebra and its applications, 2007, 426(2-3): 667-673.

[4] SHIVAKUMAR P N, WILLIAMS J J, YE Q, et al. On two-sided bounds related to weakly diagonally dominant M-matrices with application to digital circuit dynamics[J]. SIAM Journal on Matrix Analysis and Applications, 1996, 17(2): 298-312.

[5] LI W. The infinity norm bound for the inverse of nonsingular diagonal dominant matrices[J]. Applications Math. Letter, 2007, 21(2): 258-263.

[6] HUANG T Z, ZHU Y. Estimation of ||-1||¥for weakly chained diagonally dominant M-matrices[J]. Linear Algebra and its applications, 2010, 432(2-3): 670-677.

[7] CHENG GUANGHUI, TAN QIN, WANG ZHUANDE. Some inequalities for the minimum eigenvalue of the Hadamard product of an M-matrix and its inverse[J]. Journal of Inequalities and Applications, 2013, 65(1): 1029-1035.

(责任编辑：饶 超)

Further Research on the Upper Bounds for the Infinity Norms of-matrices

ZHOU Ping, HUANG Weihua

(School of Mathematics, Wenshan University, Wenshan 663000, China)

According to the properties of-matrix and the definition of infinity norm, some upper bounds for strictly diagonally dominant-matrices are further researched, and the corresponding new results are given. At the same time new lower bounds on the smallest eigenvalue of-matrixis derived. Theory analysis and numerical figure showed that the theorem one and two in this paper improve the existing results in some cases.

-matrix; Diagonal dominance; Infinity norm; Minimum eigenvalue

O151.21

A

2095-4476(2015)05-0009-03

2014-12-15 ;

2015-01-08

云南省科技厅应用基础研究青年项目(2013FD052); 云南省教育厅项目(2013Y585); 文山学院重点学科数学建设项目(12WSXK01)

周 平(1987— ), 女, 云南永平人, 文山学院数学学院讲师.