基于扩展Kalman滤波的单领航者自主水下航行器协同导航判别式训练方法研究
杨少凡 余华兵 陈新华 孙长瑜
基于扩展Kalman滤波的单领航者自主水下航行器协同导航判别式训练方法研究
杨少凡①②余华兵*①陈新华①孙长瑜①
①(中国科学院声学研究所 北京 100190)②(中国科学院大学 北京 100049)
单领航者自主水下航行器(AUV)协同导航算法中,系统模型是非线性的,扩展Kalman滤波(EKF)是针对非线性系统的很有影响力的滤波算法,但是,EKF算法的性能严格依赖于一系列模型参数,而这些参数往往需要花费很大的代价来捕获,并且常需要人工调整。该文应用一种能自动学习Kalman滤波噪声协方差参数的方法,通过仿真分析,证明了该学习算法可以完全自主并且高效、准确地输出Kalman滤波噪声参数,进一步提高了单领航者AUV协同导航系统的导航精度。
自主水下航行器;协同导航;扩展Kalman滤波;自动学习噪声参数
1 引言
随着人工智能理论、传感器和微计算机等技术的不断成熟和发展,具有感知思维和动作能力的自主水下航行器(AUV)在军事和民用领域得到了广泛的应用,如海洋勘测、水下情报搜集、远程水下攻击等。就当前的技术而言,水下导航问题仍然是AUV所面临的主要挑战之一。目前在水下环境中,AUV主要导航方法有航位推算与惯性导航方法、水声导航方法、地球物理导航方法、仿生学导航方法和组合导航方法等[1,2]。单一导航系统往往很难满足现代水下的导航要求,组合导航针对每种单一导航系统都有各自的独特性能和局限性,把几种单一系统组合起来,利用多种信息源,构成一种有多余度和导航精确度更高的多功能系统[3]。新的数据处理方法,特别是Kalman滤波(KF)[4]方法的应用是实现组合导航的关键。
本文研究有关EKF的一个基本问题:优化系统模型参数来提高从AUV状态估计精度[5]。实际应用中即使状态预测方程和观测方程可以精确建模,准确估计噪声协方差往往非常地困难。噪声往往由若干不同的因素产生:(1)附加噪声的测量数据;(2)未被EKF建模的隐含环境状态信息;(3)时间离散化引入的附加噪声;(4)EKF算法本身的近似,如常用Taylor公式进行线性近似。所有这些因素都会在状态估计和观测数据时引入干扰,在EKF中,它们通常被看作噪声。
本文研究了3个学习算法,均应用从AUV的GPS定位信息来学习EKF的协方差参数。基本思想很直观:训练EKF来最大化它的预测精度,预测精度通过训练中获取的参考数据来评估。
2 基于扩展Kalman滤波的单领航者AUV协同导航算法
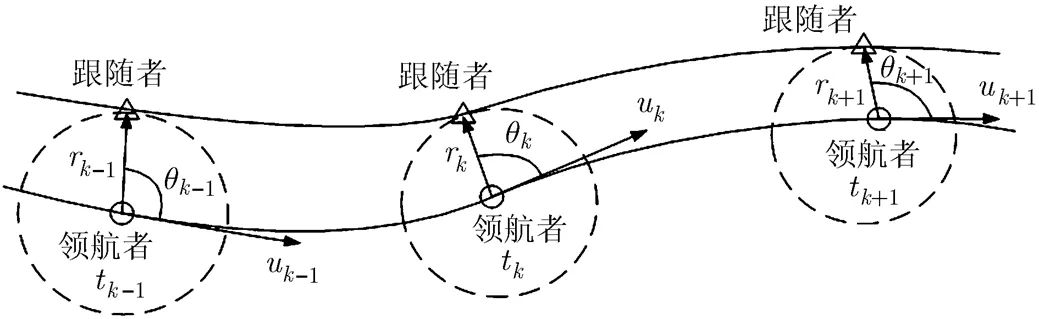
图1 AUV的仿真真实路径
扩展Kalman滤波过程可以表示为
预测过程:

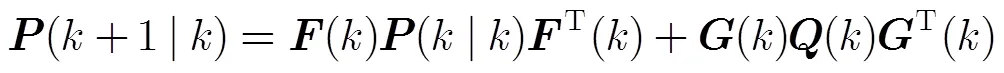
更新过程:
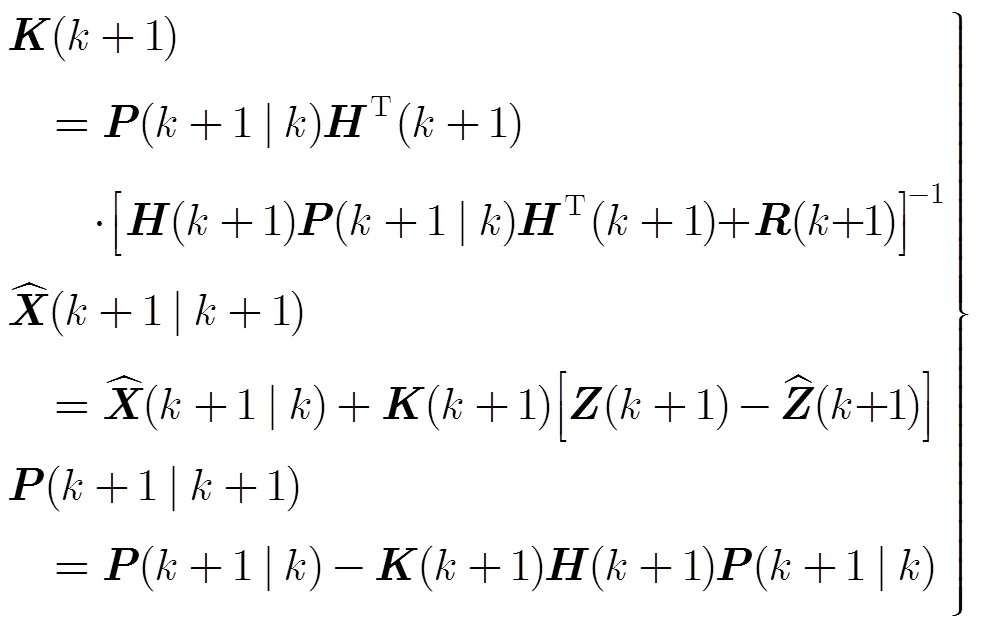

3 自动学习EKF滤波参数
本节讨论自动捕获Kalman滤波的噪声参数的学习算法。虽然接下来要讨论的算法也可以应用到更广泛的方面,但为了研究简单,我们只专注于学习噪声参数和。除已有研究成果中所需要的测量数据外,此算法还需要一个能够精确测量从AUV状态的全部变量或部分变量的测量设备。换言之,在EKF学习阶段,我们可以获得额外的变量,每个变量由映射得到
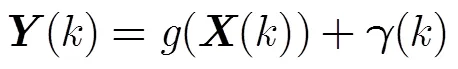
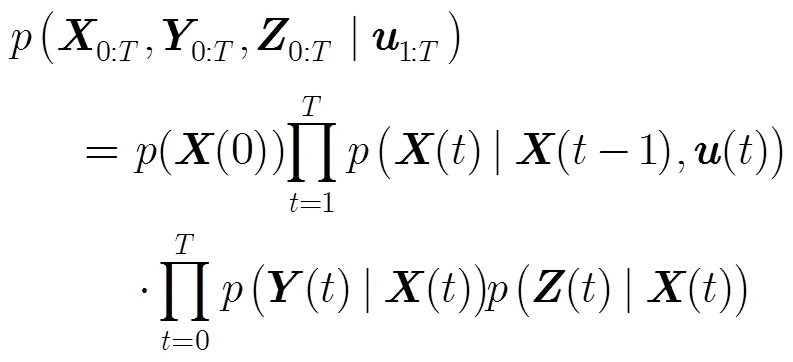
3.1最大化联合似然算法
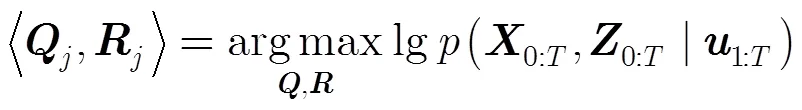

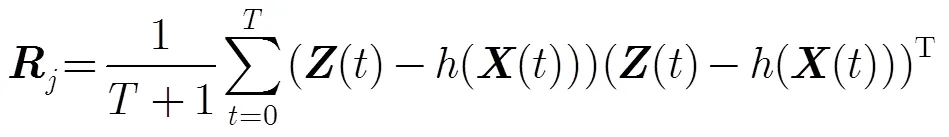
可以观察到,该算法实际上并没有真正地训练EKF,而是简单地训练滤波器元素。因此,这暗示了我们假想独立训练滤波器元素和整体训练EKF滤波器的效果相同。
3.2最小化残余预测误差算法
最大化联合似然函数算法仅当可以测量完整的状态向量时才可以应用。但是,往往将完整状态向量映射到低维的状态向量,比如单领航者协同导航系统中,完整的状态向量还包含航向角,这项不能直接由GPS数据获得。此外,最大化条件似然函数的算法实际上并没有真正运行EKF滤波器,特别地,若噪声项是相关的,这将影响算法性能。
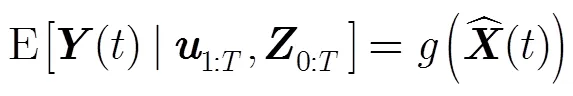
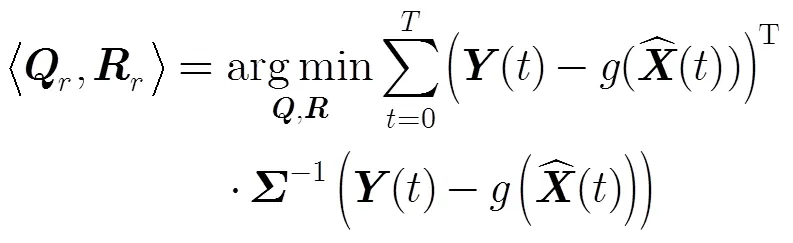
求解这个优化问题比最大化联合似然要困难得多,因为误差函数不是简单的和的函数,而是通过状态估计均值这个中间项来调节,并且是和的复杂函数。因此,这个学习算法真正评估了EKF的性能,而不是它的独立元素。
3.3 最大化预测似然算法
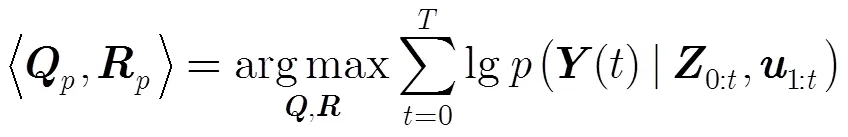
最大化lg似然函数变为
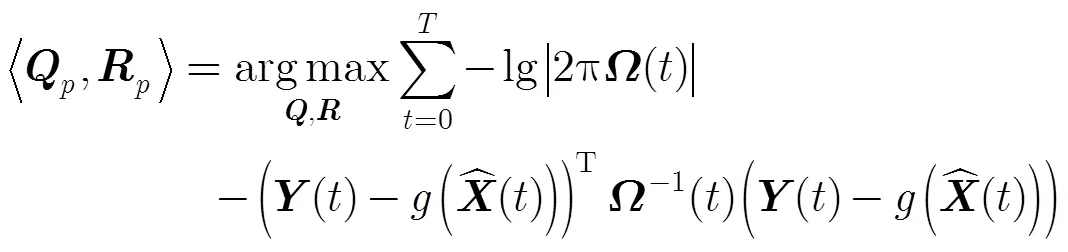
本文算法与最小化残余预测误差算法的不同之处是需要额外提供给EKF协方差矩阵参数,以此来反映状态估计量的稳定性。
4 数值仿真分析
为验证自动学习EKF滤波参数3个算法的有效性,进行了仿真研究。如图2所示,领航者AUV由坐标原点出发沿直线航行,跟随者AUV的航程分为两段,首先沿斜线航行一段距离,然后与领航者保持平行航行。在两段航程中跟随者AUV的航向角分别为和。主、从AUV的航速均为2.5 m/s,系统的状态更新时间。仿真中假设所有误差均为零均值高斯噪声。从AUV的速度信息通过测量自身推进器的转速获得,误差为。主、从AUV的航向角信息由陀螺仪测量,,。AUV间的相对距离通过水声通信测量,相对方位通过声波相位差量测,设声速为定值,取和。GPS量测噪声分别为和。
下面将分别研究初始系统可以获得精确的噪声参数和获得的噪声参数存在较大误差时3个学习算法对EKF协同导航性能的影响。仿真中选择400个测试点进行导航性能分析,并采用RMS误差进行度量。
表1初始获得精确的噪声协方差参数时各算法定位误差

协同导航算法RMS误差(m) EKF13.2 最大联合似然15.8 最小残余预测误差12.5 最大预测误差12.6
4.1初始时刻系统可获得精确的噪声协方差参数时算法性能分析
仿真结果表明,当初始给定协方差参数准确时,EKF滤波算法的RMS误差大约为13.2 m;最大联合似然算法的RMS误差约为15.8 m,误差比EKF算法大,这是由于该算法并没有真正训练EKF滤波器,而是训练独立的滤波器元素,并假设这两者等价,而实际的协同导航系统不完全服从该假设(比如存在相关噪声),因此带来较大误差;最小残余预测误差算法与最大预测误差算法的RMS误差要小于EKF算法,这是由于通过训练EKF滤波器获取了更优的噪声协方差参数,即提取了EKF内部的关联信息,从而提高了导航精度。
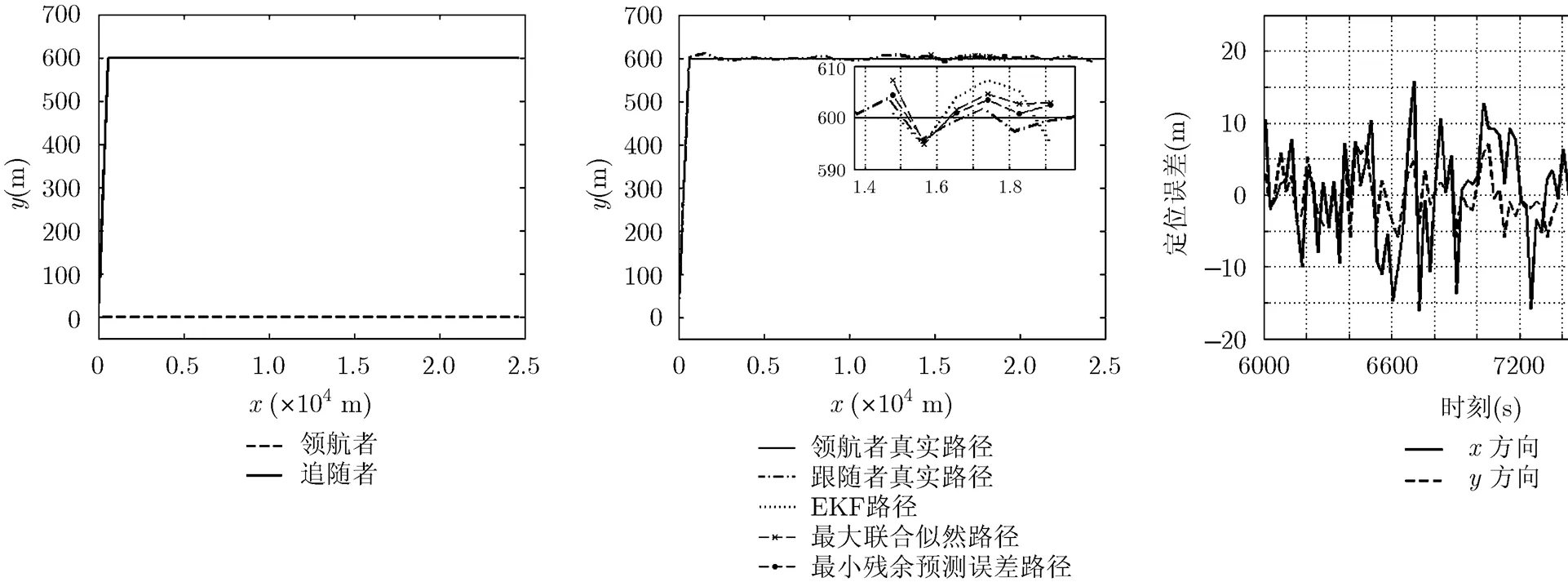
图2 AUV的仿真运动路径 图3 从AUV的协同导航轨迹 图4 EKF算法定位误差

图5 最大化联合似然算法定位误差 图6 最小残余预测误差算法定位误差 图7 最大化预测似然算法定位误差
4.2 初始时刻系统获得的噪声协方差参数与实际参数存在较大偏差时算法性能分析
实际情况下,初始噪声协方差参数很难获得准确值,往往存在较大误差。假设实际的噪声协方差参数分别为
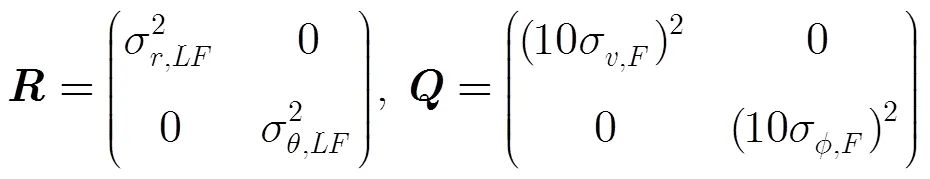
仿真结果表明,当初始时刻不能获取准确的噪声协方差参数时,EKF滤波算法的RMS误差大约为20.0 m。3个学习算法的RMS误差分别为15.6 m, 13.0 m与13.2 m,可见学习算法大大提高了单领航者AUV协同导航系统的性能。
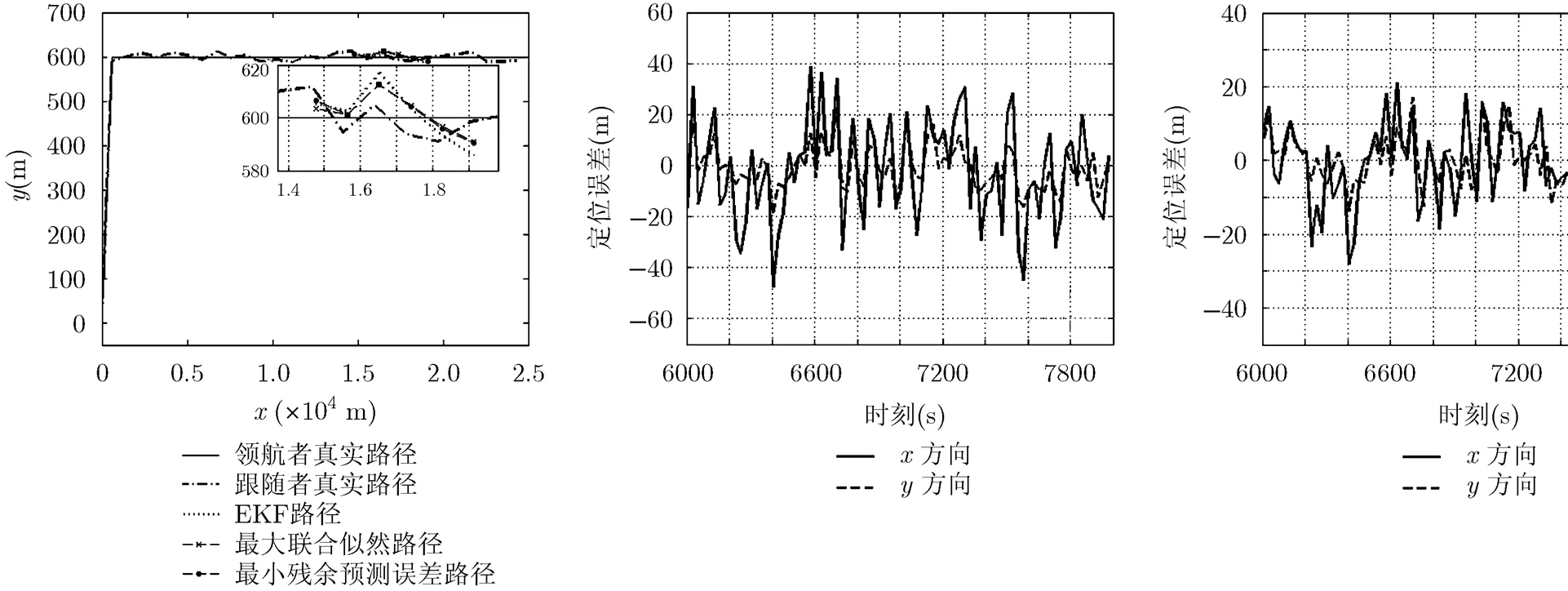
图8 从AUV的协同导航轨迹 图9 EKF算法定位误差 图10 最大化联合似然算法定位误差
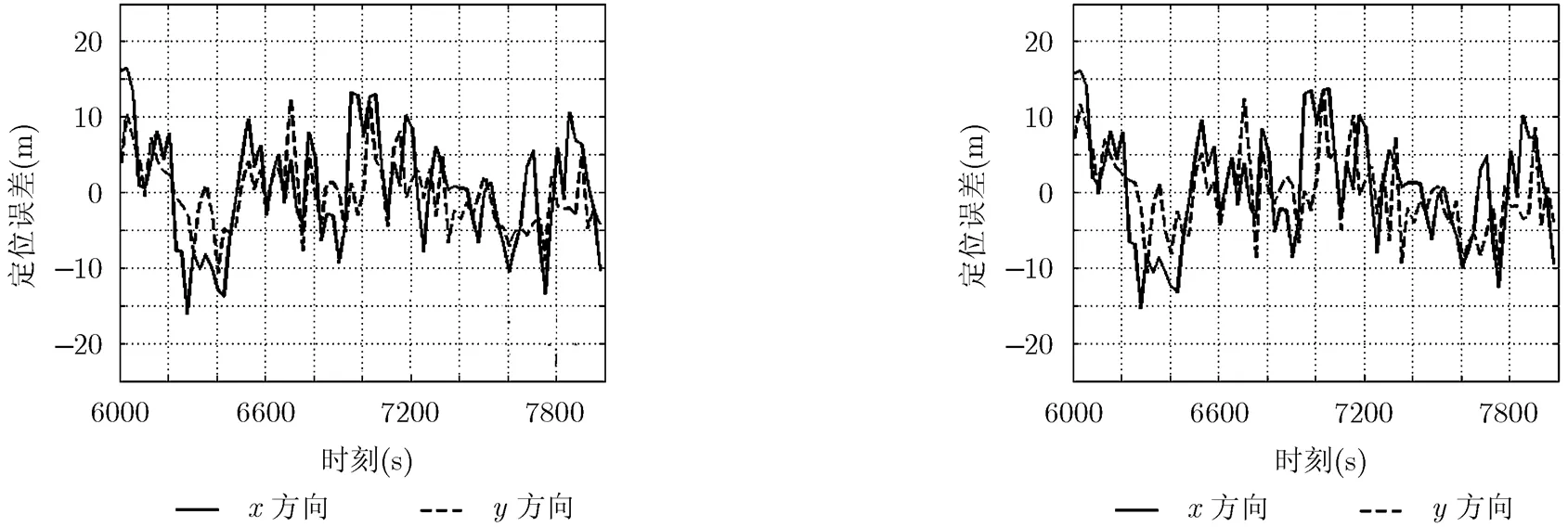
图11 最小残余预测误差算法定位误差 图12 最大化预测似然算法定位误差
表2初始误差协方差参数设为大误差值时算法定位误差

协同导航算法RMS误差(m) EKF20.0 最大联合似然15.6 最小残余预测误差13.0 最大预测误差13.2
5 结束语
本文应用一系列算法来训练EKF的噪声参数。所有的算法有相同的思想:通过调整EKF的噪声协方差参数来最大化系统状态预测精度。仿真结果表明,训练算法与常规EKF算法相比有两个优点。第一,它完全自动搜索噪声协方差参数,解决了人工调节费时费力的缺点。第二,通过训练学习获得的噪声协方差参数比初始的噪声参数更优,从而提高了协同导航系统精度。
[1] Paull L, Saeedi S, Seto M,. AUV navigation and localization: A review[J].,2014, 39(4): 131-149.
[2] Liu Ming-yong, Li Hong, and Liu Kun. Geomagnetic navigation of AUV without a priori magnetic map[C]. MTS/ IEEE OCEANS, Taipei, 2014: 1-5.
[3] 刘明雍. 水下航行器协同导航技术[M]. 北京: 国防工业出版社, 2014: 1-117.
Liu Ming-yong. Cooperative Navigation Technology for Underwater Vehicles[M]. Beijing: National Defence Industry Press, 2014: 1-117.
[4] Kalman R. A new approach to linear filtering and prediction problems[J].,1960, 82(Series D): 35-45.
[5] Abbeel P, Coates A, Montemerlo M,. Discriminative training of Kalman filters[C]. Robotic: Science and Systems, Cambridge, 2005: 289-296.
[6] Zhang Li-chuan, Xu De-min, Liu Ming-yong,. Cooperative navigation and localization for multiple UUVs [J]., 2009, 8(3): 216-221.
[7] Fallon M, Papadopoulos G, Lenorad J,. Cooperative AUV navigation using a single maneuvering surface craft[J]., 2011, 29(12): 1461-1474.
[8] 李闻白, 刘明雍, 李虎雄,等. 基于单领航者相对位置测量的多AUV协同导航系统定位性能分析[J]. 自动化学报, 2011, 37(6): 724-736.
Li Wen-bai, Liu Ming-yong, Li Hu-xiong,.. Localization performance analysis of cooperative navigation system for multiple AUVs based on relative position measurements with a single leader[J]., 2011, 37(6): 724-736.
[9] Liu Ming-yong, Li Wen-bai, Mu Bing-xian,. Cooperative navigation for multiple AUVs based on relative range measurements with a single leader[C]. IEEE International Conference on Intelligent Computing and Intelligent Systems, Xiamen, 2010: 762-766.
[10] Liu Jian, Xu De-min, Zhang Fu-bin,. Research on cooperative navigation for multiple UUVs[C]. International Symposium on Instrumentation & Measurement, Sensor Network and Automation, Sanya, 2012: 248-251.
[11] Maki T, Matsuda T, Sakamaki T,. Navigation method for underwater vehicles based on mutual acoustical positioning with a single seafloor station[J].,2013, 38(1): 167-176.
[12] Teo K, Goh B, and Chai O. Fuzzy docking guidance using augmented navigation system on an AUV[J].,2014, 40(2): 1-13.
[13] Roumeliotis S and Bekey G. Distributed multirobot localization[J]., 2002, 18(5): 781-795.
[14] Roweis S and Ghahramani Z. A unifying review of linear Gaussian models[J].,1999, 11(2): 305-345.
Discriminative Training of Kalman Filters Based Cooperative Navigation for Multiple Autonomous Underwater Vehicles with a Single Leader
Yang Shao-fan①②Yu Hua-bing①Chen Xin-hua①Sun Chang-yu①
①(,,100190,)②(,100049,)
In the cooperative navigation algorithm for multiple Autonomous Underwater Vehicles (AUVs)with a single leader, the model of the systemis nonlinear. The Extended Kalman Filter (EKF), which is directed against the nonlinear system, is one of the most influential techniques. However, the performance of EKF critically depends on a large number of modeling parameters which can be very difficult to obtain, and are often set by manual tweaking and at a great cost. In this paper, a method for automatically learning the noise covariance of a Kalman filter is applied, and the simulation result shows that this algorithm fully automatically and quickly outputs the noise covariance, which improves the navigation accuracy of the cooperative navigation system.
Autonomous Underwater Vehicle (AUV); Cooperative navigation; Extended Kalman Filter (EKF); Automatically learning the noise parameters
TB568
A
1009-5896(2015)11-2756-06
10.11999/JEIT150036
2015-01-08;改回日期:2015-06-02;
2015-07-06
余华兵 yuhuabing@mail.ioa.ac.cn
国家自然科学基金(61372180)
The National Natural Science Foundation of China (61372180)
杨少凡: 男,1991年生,博士生,研究方向为多AUV协同导航、定位、水声阵列信号处理.
余华兵: 男,1975年生,研究员,研究方向为水声阵列信号处理.
陈新华: 男,1978年生,副研究员,研究方向为水声信号处理.
孙长瑜: 男,1954年生,研究员,研究方向为水声阵列信号处理.

