双原型离散傅里叶变换调制滤波器组的快速设计方法

蒋俊正 程小磊 欧阳缮



双原型离散傅里叶变换调制滤波器组的快速设计方法

蒋俊正*程小磊 欧阳缮

(桂林电子科技大学信息与通信学院 桂林 541004)

针对大规模的离散傅里叶变换(DFT)调制滤波器组设计算法复杂度高的问题，该文提出一种基于无约束优化的快速设计算法。该算法将两个原型滤波器的设计问题归结为一个无约束优化问题,将滤波器组的传递失真，混叠失真以及原型滤波器阻带能量的加权和作为目标函数。进而，采用双迭代机制来求解该优化问题。在单步迭代中，运用矩阵求逆的等效条件和Toeplitz矩阵求逆的快速算法，显著地降低了迭代的计算代价。仿真对比表明,与已有的设计算法相比,新算法计算代价低 ,可以得到整体性能更好的滤波器组,并且可以快速设计大规模的滤波器组。

调制滤波器组；离散傅里叶变换；原型滤波器；无约束优化；双迭代算法

1 引言

滤波器组作为多速率信号处理中的核心内容一直备受关注，其在语音、图像以及通信信号处理等方面都有着十分重要的应用。相比于一般的滤波器组，调制滤波器组的优点体现在其拥有简单的结构，并且实现起来相对容易。调制滤波器组包括余弦调制滤波器组[5,6]和离散傅里叶变换(DFT)调制滤波器组。其中，DFT调制滤波器组在处理复值信号方面更具优势[16]。在一些应用当中，期望滤波器组具备很大的通道数和长支撑的子带滤波器(即大规模滤波器组)[10,11]。在文献[7]中，通过求解一个带约束的非线性优化问题，可以得到性能较好的滤波器组，但是求解过程过于复杂，无法实现大规模滤波器组的设计。在文献[8]中，采用了双原型滤波器的设计，并且运用双迭代的算法可以快速得到令人满意的滤波器组。然而当滤波器组的通道数和原型滤波器支撑都很大时，单步迭代需要对和原型滤波器长度相等的维数的矩阵求逆，求解需要耗费大量的时间，不利于实际运用。而在文献[9]中，将设计问题归结为无约束的优化问题，运用修正的牛顿迭代法，可以快速设计得到大规模的滤波器组，但是由于采用的是单原型的滤波器组的设计，制约了其设计的自由度，无法用于设计双原型的滤波器组。

本文所考虑的滤波器组是基于双原型的滤波器而设计的。根据滤波器组的性能指标，将原型滤波器的设计问题归结为一个无约束的优化问题，目标函数是由滤波器组的混叠失真、传递失真和原型滤波器的阻带能量所导出，运用双迭代算法[8]求解。进而，在单步迭代中，运用矩阵求逆的等价条件以及Toeplitz矩阵求逆的快速算法，显著地降低了矩阵求逆的计算量。与传统的设计算法进行仿真对比发现，本算法具有更低的计算代价，得到的滤波器组有着更小的重构误差，从而可以快速而有效地设计大规模的滤波器组。

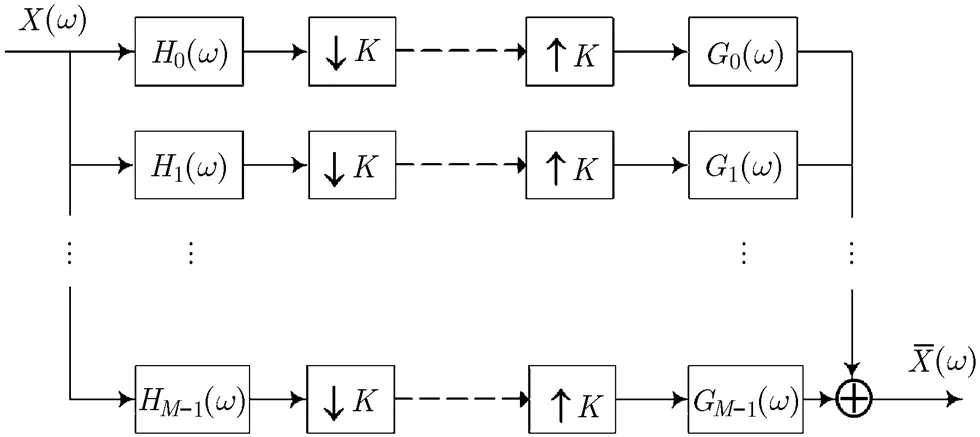
图1 M通道的DFT调制滤波器组的基本结构

2 DFT调制滤波器组的基本结构

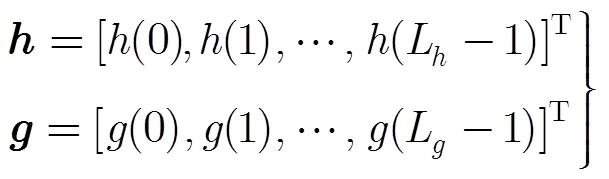
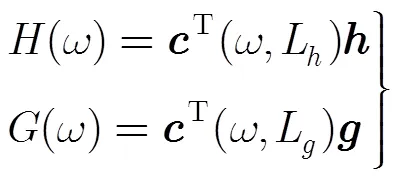
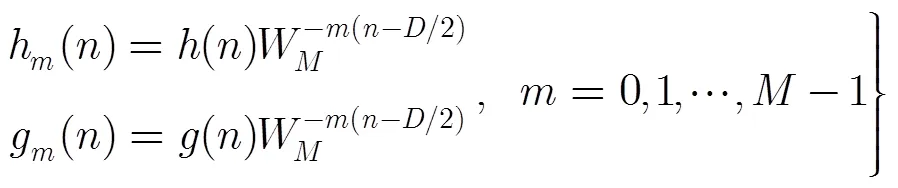
那么分析与综合滤波器的频率响应为

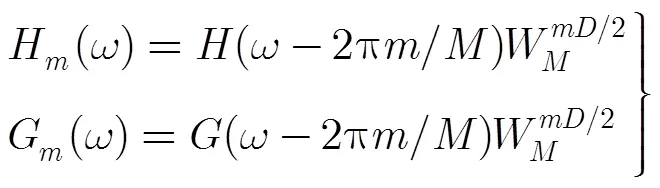
系统输入与输出的关系由式(5)给出[1]：

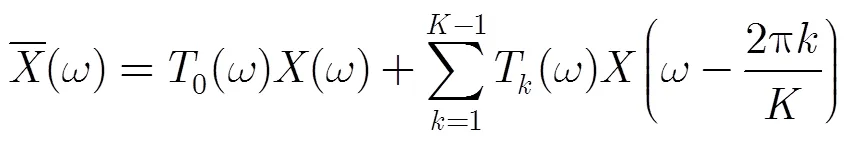
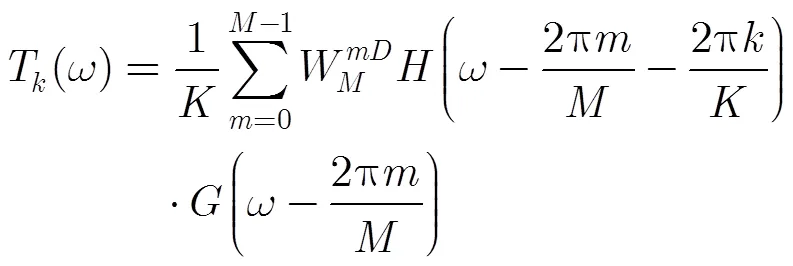
当传递函数和混叠传递函数满足式(7)：

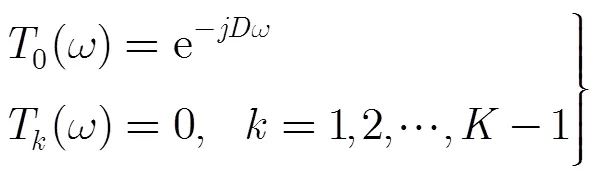
相应的滤波器组是无传递失真和混叠失真的，此时滤波器组是完全重构的。

3 DFT调制滤波器组的设计

3.1滤波器组的性能指标

在滤波器组的设计过程当中，主要考虑的是如何减小或消除各类失真现象，主要包括滤波器组的传递失真与混叠失真，这两项决定了滤波器组的重构误差。另外，期望设计得到的原型滤波器具有高的阻带衰减，高的阻带衰减可以通过控制原型滤波器的阻带能量来获得。所以本文考虑的滤波器组的性能指标有：(1)滤波器组的传递失真与混叠失真；(2)原型滤波器的阻带衰减。下面我们将逐一进行分析。

首先如果直接根据式(7)中滤波器组无传递失真和无混叠失真的频域条件来控制滤波器组的传递失真和混叠失真，那将会十分复杂。为此，考虑将无传递失真和无混叠失真的频域条件转化为时域条件来分析。

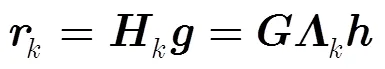
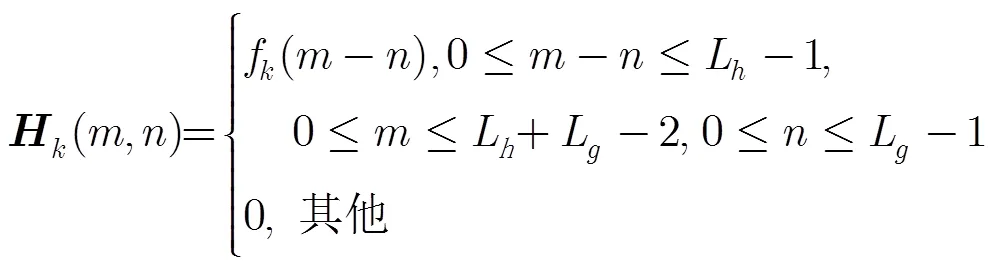
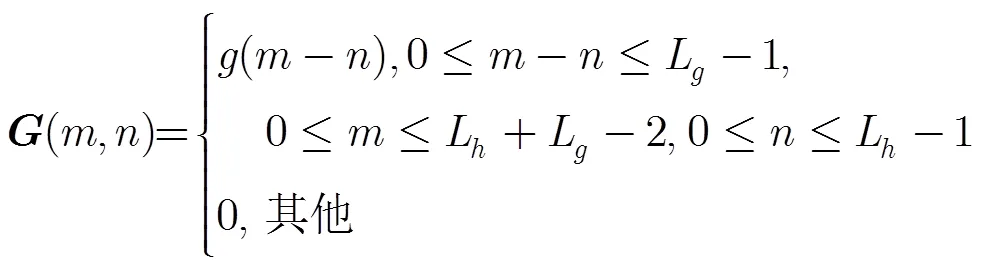
所以式(6)可以写成

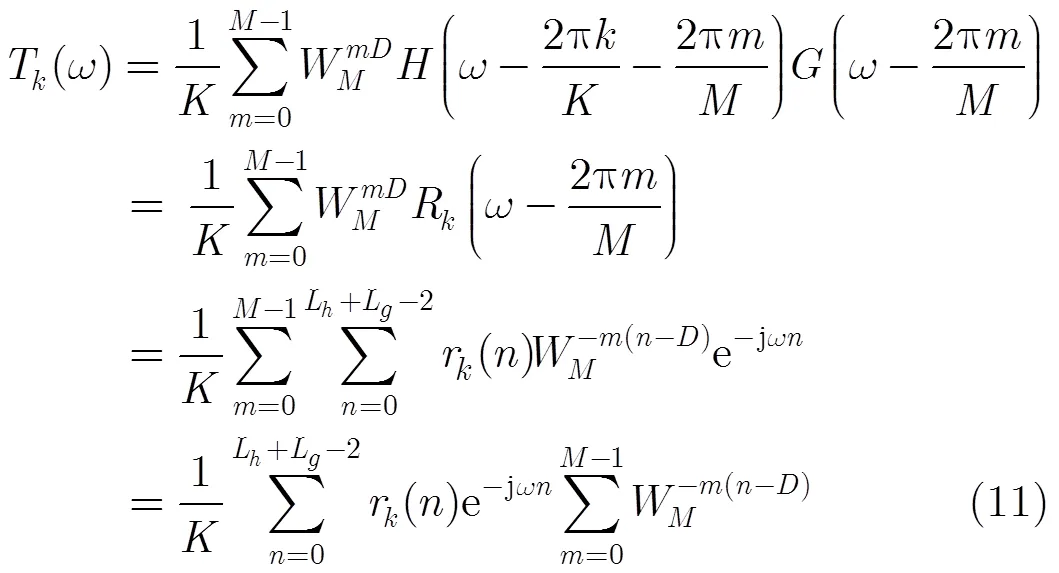
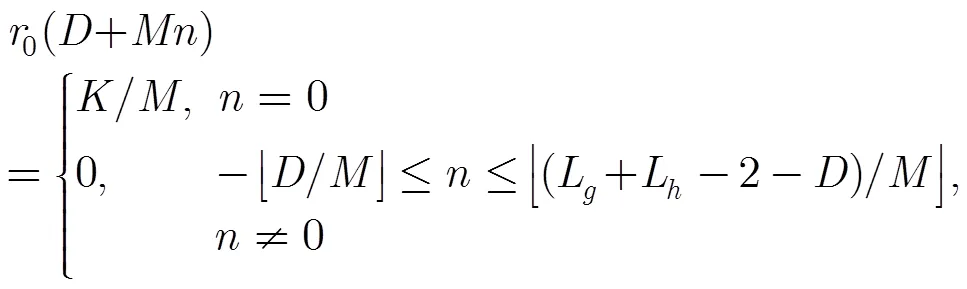
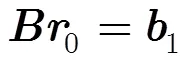
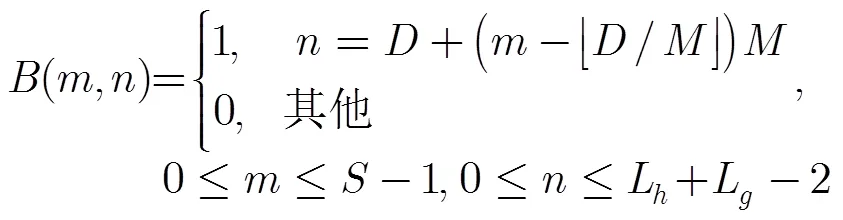
将式(15)写成矩阵相乘的形式：

基于上面的分析，在设计滤波器组中，传递失真可以由式(17)来控制。

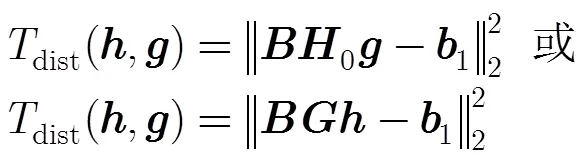
混叠失真可以由式(18)来控制。

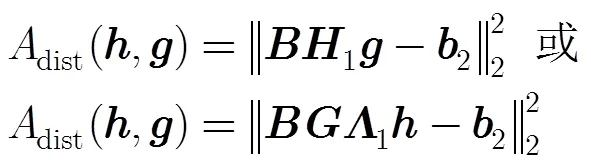
原型滤波器高的阻带衰减可以通过控制原型滤波器的阻带能量来获得，分析和综合原型滤波器的阻带能量分别表示为

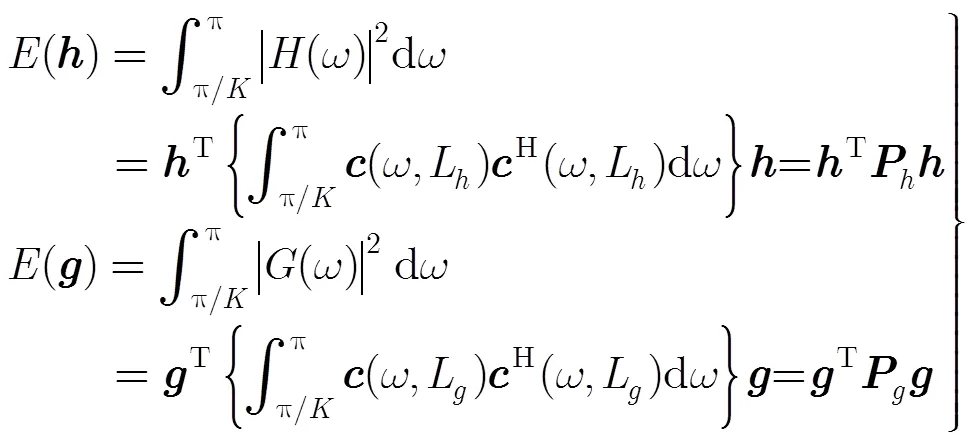
另外，原型滤波器的通带平坦性也是滤波器组的重要性能指标，本文中通过最小化滤波器组的传递失真来近似控制原型滤波器的通带平坦性，分析如下：

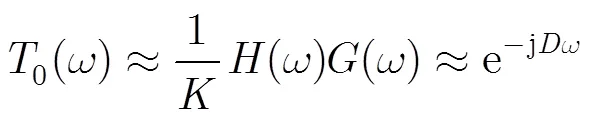
当滤波器组近似无传递失真时，可以得到

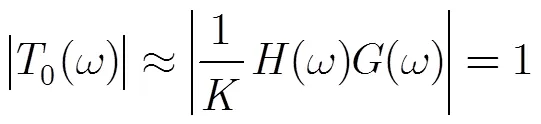
初始原型滤波器的设计问题为[9]

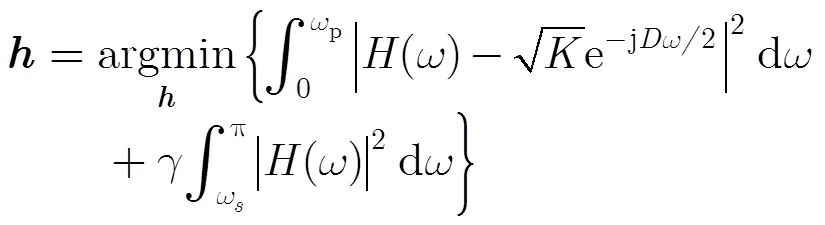
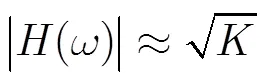
结合式(21)和式(22)，当滤波器组近似无传递失真时，可以得出，即滤波器也有良好的通带平坦性。因此，可以通过最小化滤波器组的传递失真来近似控制原型滤波器的通带平坦性。

3.2原型滤波器的设计

基于前一小节的分析，可以将原型滤波器的设计问题归结为式(23)：

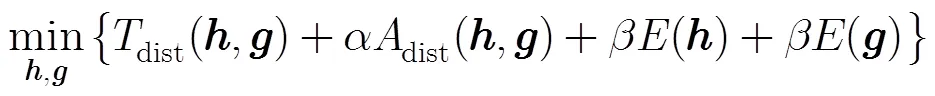
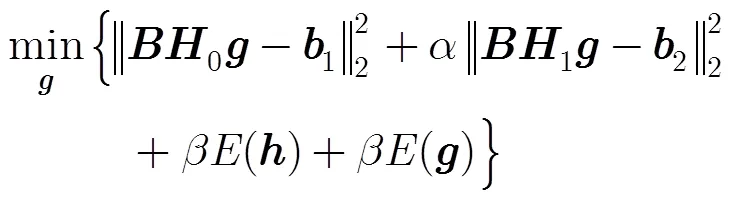
它的最优解为

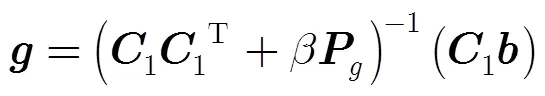
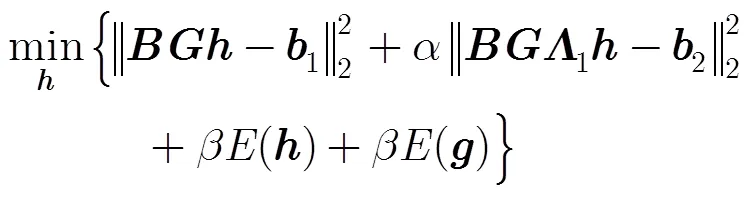
它的最优解为

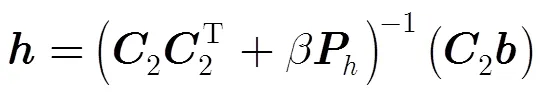
当设计的滤波器组具有很大的通道数和长支撑的子带滤波器时，式(25)和式(27)涉及大型矩阵求逆，运算量巨大。在这里我们可以运用式(28)的矩阵求逆的等效条件[18]来有效减小矩阵求逆的运算量：

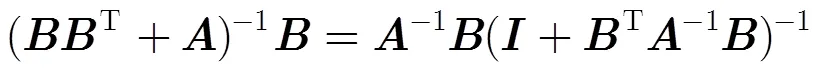
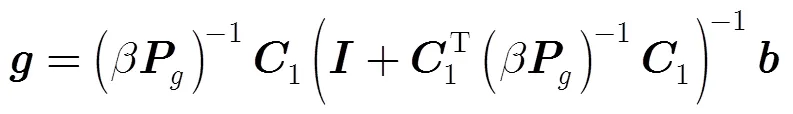
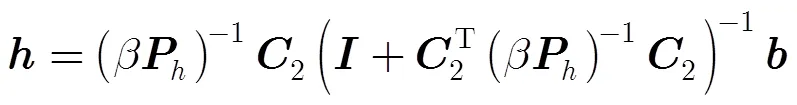
综上所述，运用如下的迭代算法来设计原型滤波器：

3.3计算复杂度分析

本文算法计算复杂度主要来自求解分析与综合原型滤波器，即式(30)和式(29)。根据矩阵求逆和矩阵相乘的计算代价，可以得出本文算法的计算复杂度为,。而在相同条件下，文献[8]算法的计算复杂度为,。可以看出当滤波器组具备很大的通道数以及长支撑的子带滤波器时(即,和都很大时)，本文方法求解原型滤波器的计算量要远小于文献[8]的方法，适用于设计大规模的滤波器组。

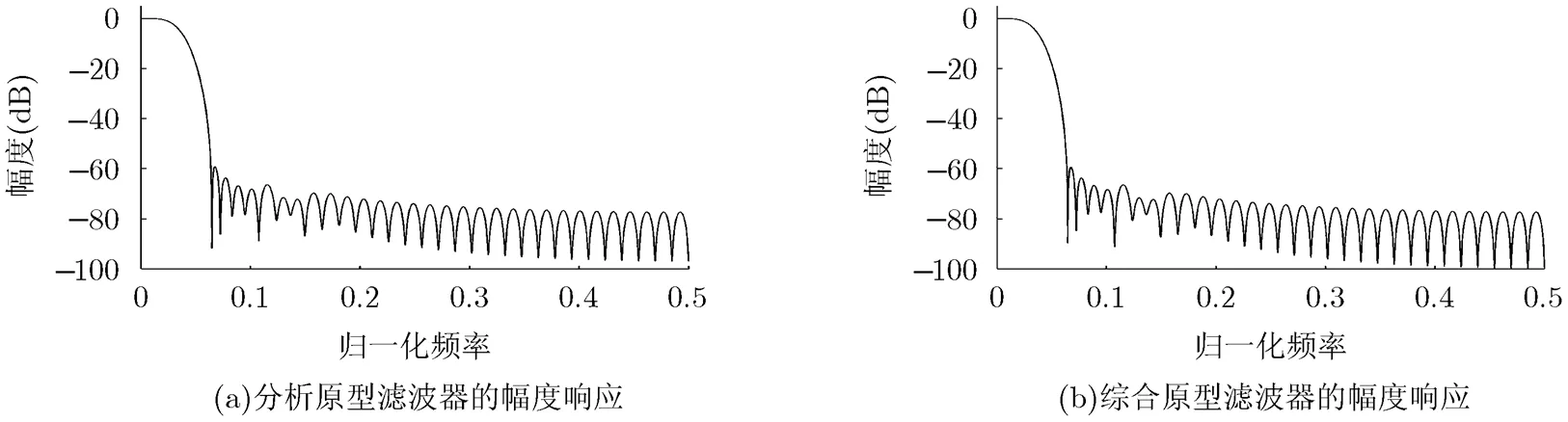
图2 例1中本文设计方法得到的原型滤波器的幅度响应

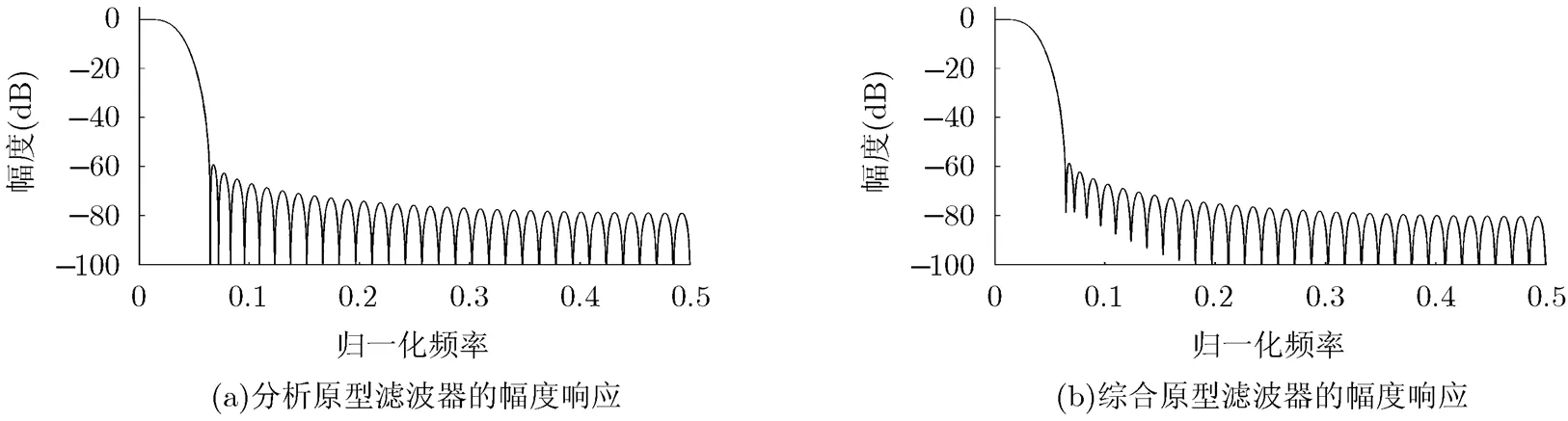
图3 例1中文献[8]设计方法得到的原型滤波器的幅度响应

表1例1中本文算法与文献[8]算法的性能与时间对比

设计算法传递失真(dB)混叠失真(dB)通带波纹(dB)阻带水平(dB)重构误差(dB)运行所耗CPU时间(s) 文献[8]算法-86.01-64.16-64.580.02 本文算法-73.49-67.61-65.430.01

4 仿真结果与分析

在这一节中，我们将本文的算法与现有的算法进行仿真对比，所有的仿真和对比都是在相同的环境下运行。

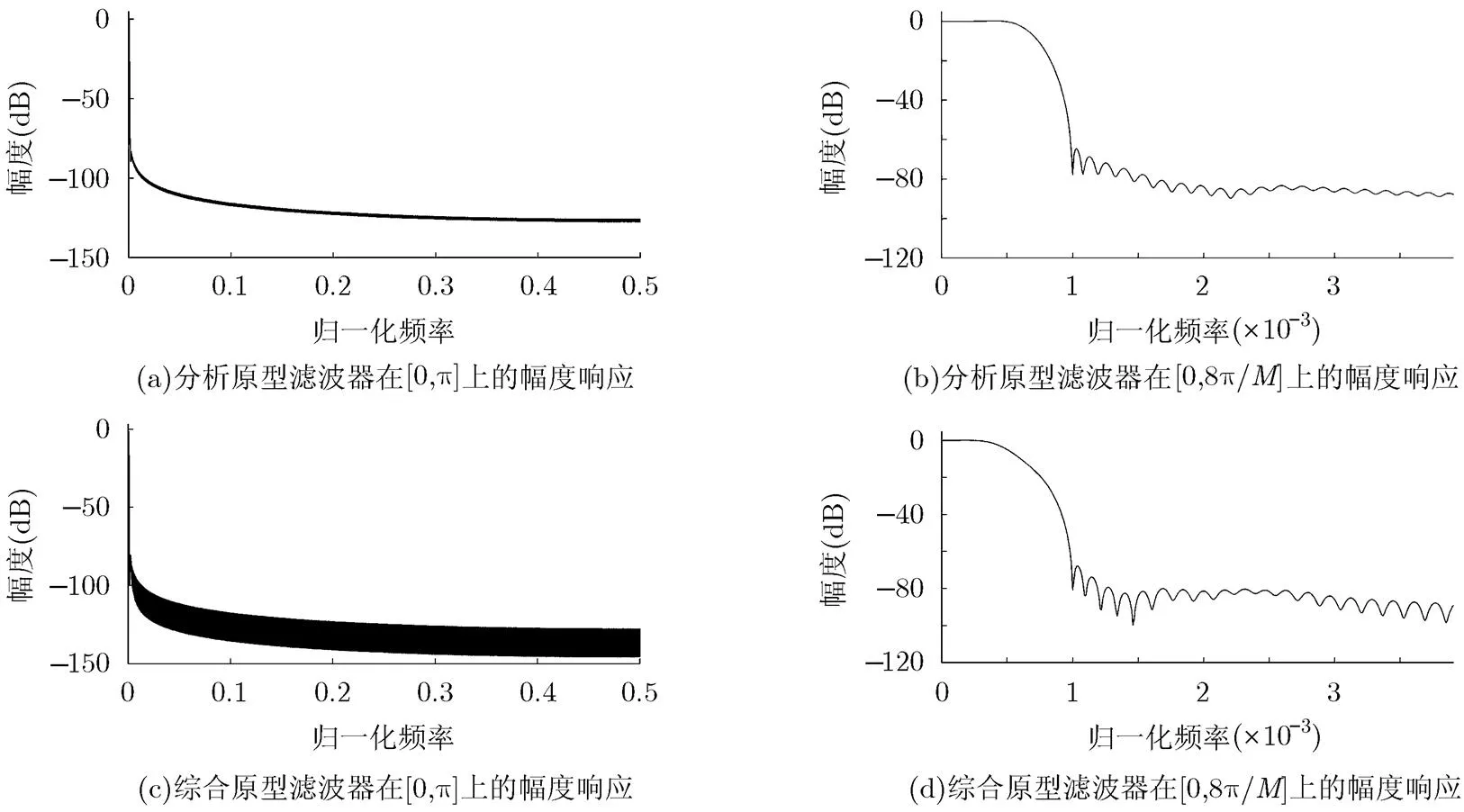
图4 例2中本文设计方法得到的原型滤波器的幅度响应

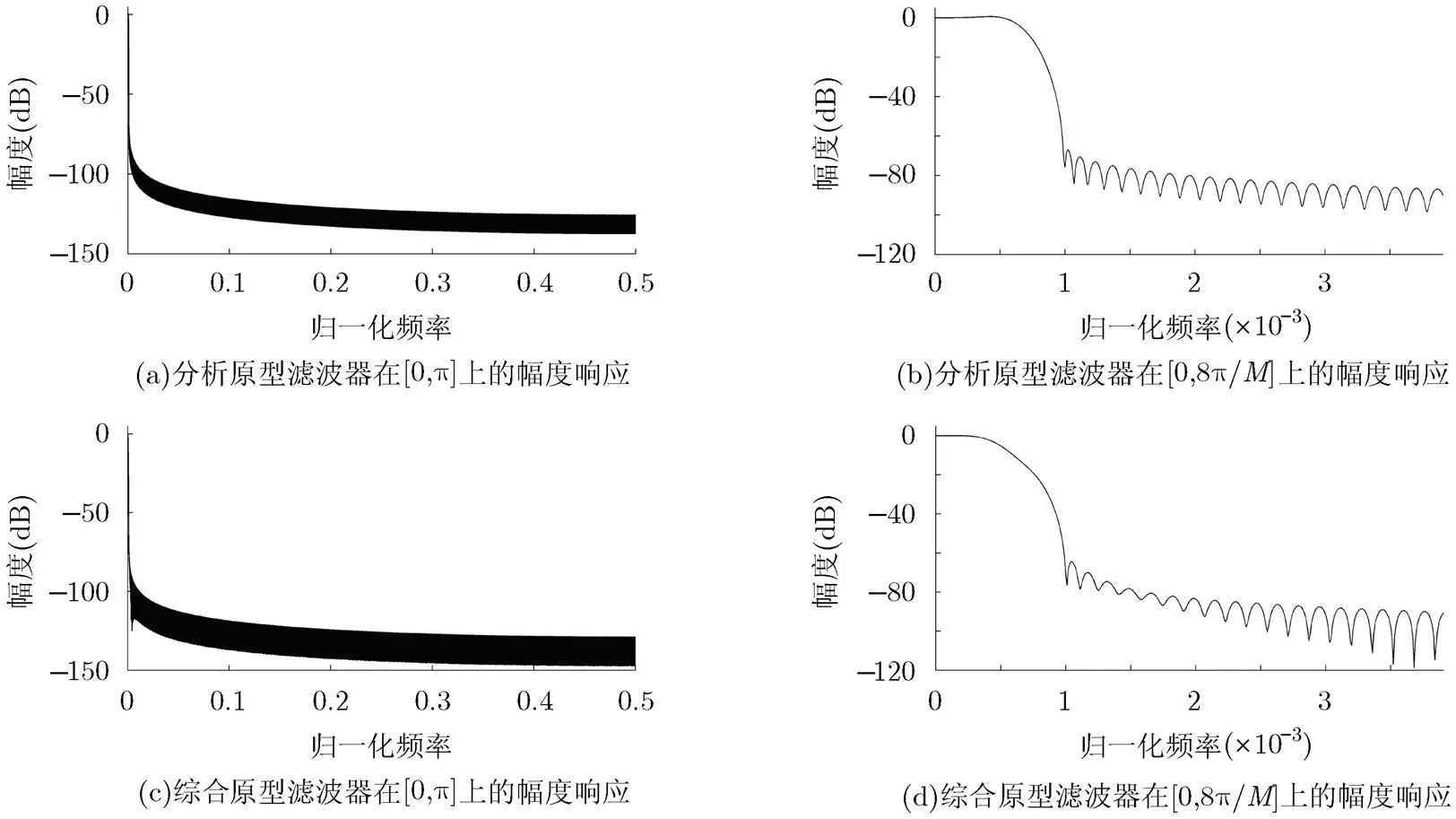
图5 例2中文献[8]设计方法得到的原型滤波器的幅度响应

表2例2中本文算法与文献[8]算法的性能与时间对比

设计算法传递失真(dB)混叠失真(dB)通带波纹(dB)阻带水平(dB)重构误差(dB)单步迭CPU时间(s) 文献[8]算法-71.84-73.80-71.28106.95 本文算法-72.48-75.63-72.60 1.41

5 结束语

本文围绕如何快速有效地设计DFT调制滤波器组的问题，提出了一种基于无约束优化的快速设计算法。理论分析和仿真结果联合表明，本文方法设计得到的滤波器组相比于现有方法有着更好的整体性能。并且，更为重要的一点，当滤波器组具备大的通道数和长支撑的子带滤波器时，新算法的计算效率相比于现有算法有着显著的提高，因此本文算法非常适合大规模滤波器组的快速设计。后续工作将考虑大规模滤波器组的实际应用问题。

[1] Vaidyanathan P P. Multirate Systems and Filter Banks[M]. Englewoo Cliffs: N.J.PrenticeHall, 1993: 188-272.

[2] 水冰, 史仪凯. 两带自适应 FIR 线性相位双正交滤波器组设计[J]. 电子与信息学报, 2006, 28(10): 1950-1954.

Shui B and Shi Y K. Design of signal-adapted two-band biorthogonal linear phase filter banks[J].&, 2006, 28(10): 1950-1954.

[3] Shui P L. Image denoising using 2-D oversampled DFT modulated filter banks[J]., 2009, 3(3): 163-173.

[4] Rajapaksha N, Madanayake A, and Bruton L T. 2D space- time wave-digital multi-fan filter banks for signals consistingof multiple plane waves[J].

, 2014, 25(1): 17-39.

[5] Jain A and Goel A. A multiobjective optimization method for designing-channel NPR cosine modulated filter bank for image compression[J]., 2015, 7(2): 93-100.

[6] Kumar A, Pooja R, and Singh G K. Design and performance of closed form method for cosine modulated filter bank using different windows functions[J]., 2014, 17(4): 427-441.

[7] Wilbur M R, Davidson T N, and Reilly J P. Efficient design of oversampled NPR GDFT filter banks[J]., 2004, 52(7): 1947-1963.

[8] 蒋俊正, 王小龙, 水鹏朗. 一种设计DFT调制滤波器组的新算法[J]. 西安电子科技大学学报, 2010, 37(4): 689-693.

Jiang J Z, Wang X L, and Shui P L.Novel method for designing DFT modulated filter banks[J]., 2010, 37(4): 689-693.

[9] Jiang J Z, Zhou F, Ouyang S,.. Efficient design of very large-scale DFT modulated filter banks using Mth band condition[J]., 2014, 8(4): 381-391.

[10] Qu D, Jiang T, and He Y. Prototype filter optimization to minimize stopband energy with NPR constraint for filter bank multicarrier modulation systems[J]., 2013, 61(1): 159-169.

[11] De Haan J M, Grbic N, Claesson I,.. Filter bank design for subband adaptive microphone arrays[J]., 2003, 11(1): 14-23.

[12] Schwerdtfeger T, Velten J, and Kummert A. A multidimensional wave digital filter bank for video-based motion analysis[J]., 2014, 25(2): 295-311.

[13] 张飞, 边东明, 张更新. 星载柔性转发器中一种近似精确重构原型滤波器的设计[J]. 电子与信息学报, 2013, 35(3): 671-676.

Zhang F, Bian D M, and Zhang G X. Design of a near perfect reconstruction prototype filter on flexible transponder for broadband satellite communications[J].&, 2013, 35(3): 671-676.

[14] 李睿, 章毓晋, 谭华春. 自适应去噪滤波器组合的训练与设计方法[J]. 电子与信息学报, 2006, 28(7): 1165-1168.

Li R, Zhang Y J, and Tan H C. A hybrid filter training and design method for adaptive noise cancellation[J].&, 2006, 28(7): 1165-1168.

[15] Eghbali A and Johansson H. On efficient design of high-order filters with applications to filter banks and transmultiplexers with large number of channels[J]., 2014, 62(5): 1198-1209.

[16] Selesnick I W, Baraniuk R G, and Kingsbury N G. The dual-tree complex wavelet transform[J]., 2005, 22(6): 123-151.

[17] Shui P L, Jiang J Z, and Wang X L. Design of oversampled double-prototype DFT modulated filter banks via bi-iterative second-order cone program[J]., 2010, 90(5): 1597-1608.

[18] Petersen K B and Pedersen M S. The matrix cookbook[OL]. http://www2.imm.dtu.dk/pubdb/p.php, 2012.11.

[19] Trench W F. An algorithm for the inversion of finite Toeplitz matrices[J].&, 1964, 12(3): 515-522.

Fast Design of Double-prototype Discrete Fourier Transform Modulated Filter Banks

Jiang Jun-zheng Cheng Xiao-lei Ouyang Shan

(,,541004,)

This paper presents an efficient algorithm to design high-complexity Discrete Fourier Transform (DFT) modulated filter bank with double-prototype. The algorithm is based on unconstrained optimization, where the design problem is formulated into an unconstrained optimization problem, whose objective function is the weighted sum of the transfer distortion, the aliasing distortion of the filter bank, and the stopband energy of the Prototype Filters (PFs). The optimization problem can be efficiently solved by utilizing the bi-iterative scheme. The matrix inverse identity and the fast algorithm for Toeplitz matrix inversion are employed to dramatically reduce the computational cost of the iterative procedure. Numerical examples and compared tests to show that compared with the existing methods, the proposed method possesses much lower computational cost and can be used to design large-scale filter bank with better overall performance.

Modulated filter bank; Discrete Fourier Transform (DFT); Prototype Filters (PFs); Unconstrained optimization; Bi-iterative scheme

TN911.7

A

1009-5896(2015)11-2628-06

10.11999/JEIT150298

2015-03-11；改回日期：2015-07-13；

2015-08-27

蒋俊正 jzjiang@guet.edu.cn

国家自然科学基金(61261032)；广西自然科学基金(2013GXNSFBA019264)

The National Natural Science Foundation of China (61261032); Guangxi Natural Science Foundation (2013GXNSFBA019264)

蒋俊正： 男，1983年生，副教授，硕士生导师，研究方向为多速率滤波器组理论与应用、通信信号处理.

程小磊： 男，1992年生，硕士生，研究方向为多速率滤波器组的设计及应用.

欧阳缮： 男，1960年生，教授，博士生导师，研究方向为自适应信号处理、通信信号处理.