基于群决策的改进AHP法在桥梁评估中的应用

屈兵，肖汝诚，仲健，林晶



基于群决策的改进AHP法在桥梁评估中的应用

屈兵，肖汝诚，仲健，林晶

(同济大学 土木工程学院，上海，200092)

针对传统层次分析法(AHP)的缺陷，提出基于群决策的改进AHP方法，应用到桥梁状态评估中。首先，引入指数区间数标度方法，建立元素为指数区间数的判断矩阵，并建立一套求解指数区间数判断矩阵指标权重的优化算法；然后，引入基于加权集值统计的专家群决策理论，讨论基于判断偏好信息的专家权重计算方法以及判断矩阵的集结，得到专家群体决策矩阵；最后，构建某钢箱梁斜拉桥的综合评估AHP模型，采用本文方法进行指标权重计算，论证方法的可行性与实用性。本文方法弱化了单一专家评判过程中的主观不确定性，为桥梁的管理养护提供了更加科学可信的决策依据。

层次分析法(AHP)；桥梁评估；指数区间数；权重；群决策；集值统计

桥梁的状态评估是一个涉及多层次、多指标、多因素的复杂决策过程。在评估过程中，由于定性评判的主观性、某些统计方法的局限性以及诸多不可定量描述的外界因素的干扰，使得桥梁的评估存在极大的模糊性与不确定性[1]。层次分析法(AHP)因其简明直观的原理与广泛的实用性在桥梁评估模型的建立与指标的权重确定中得到了学者的青睐。在JTG H11—2004“公路桥梁养护规范”[2]、CJJ 99—2009“城市桥梁养护规范”[3]以及JTG/T H21—2011“公路桥梁技术状况评定标准”[4]中均有AHP法思想的体现，但规范中对于构件指标权重的规定均为经验性取值或由经验公式算得，对于种类繁多且复杂的桥梁结构而言，这些规定难以以偏概全。传统AHP法采用1~9标度获得判断矩阵，继而求出权重，1~9标度虽然简洁，但主观性较强，容易出现评估结果的逆序、思维与判断矩阵的一致性脱节等问题[5−6]。为此，不少学者对AHP法进行了改进，提出了如标度、指数标度、分数标度、0.1~0.9标度、区间标度等多种标度体系[7−10]。吕跃进等[11]对多种标度进行了系统比较研究，指出指数标度较好地解决了判断矩阵一致性与思维一致性脱节的问题，是一种可靠优良的标度，并对指数标度理论进行了若干改进与完善。而区间标度则实现了标度值从点到空间的扩展，有效量化了问题的不确定 性[12−13]。但是在桥梁评估领域，大多仍沿用传统基于1~9标度的AHP法，存在一定的粗糙性与不合理性。本文作者将指数标度与区间标度进行有效地结合，提出基于指数区间数标度的AHP方法，建立了一套求解指数区间数矩阵指标权重的优化算法；同时引入群组判断的思想，通过多个专家构造判断矩阵，去除由于个人偏好而产生的判断偏差。将其应用于桥梁结构的评估中，使评估结果更加科学可靠。

1 指数区间数标度方法

1.1 指数标度

韦伯−费希纳定律[14]认为：心理量是外界刺激量的对数函数，即当刺激强度以几何级数增加时，感觉的强度以算术级数增加。感觉强度与刺激强度之间的函数关系为

其中：为韦伯常数。根据此定理，若将指标a相对于a的重要性程度(假定a的重要性大于等于a的重要性)等间距地分成9个等级，分别为“同等重要”、“稍微重要”、“明显重要”、“非常重要”、“极端重要”，以及它们的中间程度等级，并用=0~8的等差整数分别描述这9个等级，那么，指标a对a的客观重要性比率a与的关系为

1.2 指数区间数判断矩阵的建立

指数标度方法可获得与思维判断的一致性，但比较判断结果仍为确定的值。为适应评价过程的模糊性与随机性，采用区间数来量化人们的主观判断，这时判断矩阵中各元素均为指数型区间数。有如下定义：

表1 指数区间数标度

由表1可知：当重要性等级相差越大时，标度区间的间距越大，标度的不确定度也越大，这符合人的思维判断规律。

1.3 一致性逼近及指标权重计算

1)为满足完全一致性的确定性数字矩阵；

2) 矩阵与最可能值数字矩阵(见定义2)的偏差尽可能小；

这样，对矩阵模型的一致性逼近转化为最优化计算问题。其中的目标函数用于反映与的偏差。引入矩阵各元素区间数的偏差项l，令：

式中：=1, 2, …,；=1, 2, …,。

可以得到矩阵与的偏差函数为

由于判断矩阵具有互反性，这里只需考虑矩阵的上三角元素(不包含对角线元素)。

式中：=1, 2, …,;=1, 2, …,。

求解上述最优问题，可得到最优权重向量。

2 基于群决策的区间数判断矩阵集结

实际评判中，单一专家往往不能充分反映客观事实，因此，需要综合多个专家的意见，这就出现了群体决策的问题。群决策的过程，就是将各专家意见的分歧统一化，极小化群决策结果与个人偏好的不一致的过程[15−16]。

2.1 基于集值统计的判断矩阵集结模型

集值统计是处理不确定性评价指标的一种有效方式。设评价系统各评判指标集合为={1,2, …,x, …,x}，评审专家集为={1,2, …,s, …,s}。对每一个评判指标()，各专家()给出的区间估计值为(=1, 2, …,)，这样可形成一个维集值统计序列。将这个区间叠加在一起，并令，，则个专家对指标的评判在数轴上形成一个位于区间上的随机分布。区间上任一点的模糊覆盖率如图1所示。

图1 评价指标值的落影分布

式中：

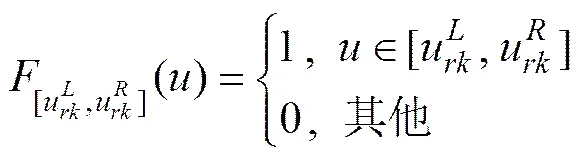
将式(10)化简整理得

2.2 专家权重的确定

专家权重可通过专家构造的判断矩阵间接反映出来，具体表现在专家的个体偏好信息与综合偏好信息的差异上。为定量体现这种差异，定义2个区间数，的偏离度为

对不同的指标，同一专家评判结果的偏离度是不一样的。一般认为，各专家的主观理性判断存在着一致性的趋势，而不一致性评价矩阵的产生可以认为是由众多的随机干扰共同作用的结果。设专家给出的各指标的评判区间与对应各指标的总体加权评判区间的相对偏差为，对进行如下假设。

2.3 专家群体决策矩阵的建立

专家群体决策矩阵的建立步骤如下。

3 应用实例

以一座钢箱梁斜拉桥的三层AHP评估模型为例，采用本文方法计算评估指标的权重。评估模型如图2所示。

图2 钢箱梁斜拉桥状态评估模型

决策者可根据需要对各层次单元进行进一步的分解、综合或修改。如可将“混凝土质量”继续细分为混凝土强度推定值、钢筋锈蚀情况、氯离子含量、混凝土电阻率、混凝土保护层损伤、碳化程度以及表观缺损等。以下仅以第1层的5个指标(索塔、钢箱梁、斜拉索、墩台基础和附属设施)为例进行计算说明。

1) 对第1层各指标进行两两比较判断，得到5阶主观感觉判断矩阵。6位专家填写的主观感觉判断矩阵如下。

专家一：

专家二：

专家三：

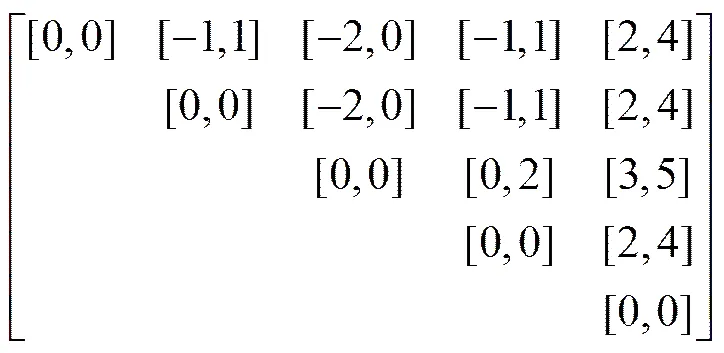
专家四：

专家五：

专家六：

2) 根据式(17)计算各专家权重，结果见表2。

表2 专家权重

3) 取矩阵上三角元素，共10个评价指标(记为1~10)，根据式(18)计算出各指标的群决策综合评判区间，结果见表3。

表3 综合评判区间与置信度

5) 计算各指标的权重，结果见表4。

表4 各指标权重

表4中，“AHP权重”为按照本文方法计算的权重；“规范权重”为根据JTG/T H21—2011“公路桥梁技术状况评定标准”[4]中相关规定得到的斜拉桥构件权重。

由表4可以看到：“AHP权重”中各指标的权重由大到小排列顺序为斜拉索、索塔、钢箱梁、墩台基础、附属设施。上部结构各指标(索塔、钢箱梁与斜拉索)的AHP计算权重均比墩台基础的大，且远大于附属设施的AHP计算权重，这与各专家给出的主观感觉判断矩阵中反映出的指标重要性排序是一致的，说明该桥更加重视对上部结构安全性性能的评价。而“规范权重”中的指标的权重由大到小排序为墩台基础、附属设施、斜拉索、索塔、钢箱梁。墩基与附属设施的权重显著大于“AHP权重”的计算结果，而上部结构各构件权重则较小，这与专家群体对该桥构件的重要性判断是不相符的，原因在于规范中对各类桥型的构件权重规定是一成不变的，显然不能反映出不同桥梁评估时的侧重点与差异性。

本文方法针对实际桥梁，综合了不同专家的意见，并合理量化了判断与思维的一致性与判断的模糊性，因而更具科学性与可靠性。

根据上述方法，可求得AHP模型中其他单元层次的指标权重。

逐级向上综合，便可得到桥梁的整体评估结果。评价结果的确定与综合可结合变权理论[18]、模糊理 论[19]等进行。

4 结论

1) 提出基于指数区间数的不确定型AHP法，建立了一套求解指数区间数判断矩阵指标权重的优化算法，使决策者的思维与判断结果取得一致，弱化了判断中的不确定性。

2) 引入专家的群组判断，提出基于专家权重的集值统计方法，建立了专家群体决策矩阵，避免了单一专家模型评判的不足。

3) 用实例论证了方法的可操作性与实用性。本文方法也适用于其他各类基于AHP方法的综合评估。更多的工程应用与验证将在今后的研究中进一步展开。

[1] HUANG Qiao, REN Yuan, LIN Yangzi. Application of uncertain type of AHP to condition assessment of cable-stayed bridges[J]. Journal of Southeast University (English Edition), 2007, 23(4): 599−603.

[2] JTG H11—2004, 公路桥涵养护规范[S].
JTG H11—2004, Code for maintenance of highway bridges and culvers[S].

[3] CJJ 99—2009, 城市桥梁养护技术规范[S].
CJJ 99—2009, Technical code of maintenance for city bridge[S].

[4] JTG/T H21—2011, 公路桥梁技术状况评定标准[S].
JTG/T H21—2011, Standards for technical condition evaluation of highway bridges[S].

[5] Ishizaka A, Labib A. Review of the main developments in the analytic hierarchy process[J]. Expert Systems with Applications, 2011, 38(11): 14336−14345.

[6] Chan K Y, Kwong C K, Wong Y. Computational intelligence techniques for new product design[M]. Heidelberg: Springer, 2012: 79−93.

[7] BAI Hanbin, WANG Nuanchen. Research on the Selection of Scale in AHP[C]// The 3rd International Conference on Advanced Computer Theory and Engineering (ICACTE), Chengdu: IEEE, 2010: V6-108−V6-111.

[8] Ishizaka A, Balkenborg D, Kaplan T. Influence of aggregation and measurement scale on ranking a compromise alternative in AHP[J]. Journal of the Operational Research Society, 2011, 62(4): 700−710.

[9] 鲍广宇, 连向磊, 何明, 等. 基于新型语言评估标度的二元语义改进模型[J]. 控制与决策, 2010, 25(5): 780−784.
BAO Guangyu, LIAN Xianglei, HE Ming, et al. Improved two-tuple linguistic representation model based on new linguistic evaluation scale[J]. Control and Decision, 2010, 25(5): 780−784.

[10] 胡文发, 姚伟, 周明. 基于模糊层次分析法的既有住宅性能综合评价[J]. 同济大学学报(自然科学版), 2011, 39(5): 785−790.
HU Wenfa, YAO Wei, ZHOU Ming. Comprehensive evaluation on performance of existing residential buildings based on fuzzy and analytic hierarchy process[J]. Journal of Tongji University (Natural Science), 2011, 39(5): 785−790.

[11] 吕跃进, 陈万翠, 钟磊. 层次分析法标度研究的若干问题[J]. 琼州学院学报, 2013, 20(5): 1−6.
LÜ Yuejin, CHEN Wancui, ZHONG Lei. Research on some problems of the scale of analytic hierarchy process[J]. Journal of Qiongzhou University, 2013, 20(5): 1−6.

[12] Sironen S, Leskinen P, Kangas A, et al. Variation of preference inconsistency when applying ratio and interval scale pairwise comparisons[J]. Journal of Multi-Criteria Decision Analysis, 2014, 21(3/4): 183−195.

[13] LIN Liang, WANG Chao. On consistency and ranking of alternatives in uncertain AHP[J]. Natural Science, 2012, 4(5): 340.

[14] Saaty T L, Vargas L G. Models, methods, concepts and applications of the analytic hierarchy process[M]. 2nd ed. New York: Springer, 2001: 27−46.

[15] DONG Yucheng, ZHANG Guiqing, Hong W C, et al. Consensus models for AHP group decision making under row geometric mean prioritization method[J]. Decision Support Systems, 2010, 49(3): 281−289.

[16] Pedrycz W, Song M. Analytic hierarchy process (AHP) in group decision making and its optimization with an allocation of information granularity[J]. IEEE Transactions on Fuzzy Systems, 2011, 19(3): 527−539.

[17] ZHANG Zhaoning, MENG Na, ZHOU Peng. Based on the fuzzy set-valued statistics and the fuzzy mathematics theory in air traffic control system safety appraisal application[J]. Physics Procedia, 2012, 33: 511−520.

[18] 李春好, 孙永河, 贾艳辉, 等. 变权层次分析法[J]. 系统工程理论与实践, 2010(4): 723−731.
LI Chunhao, SUN Yonghe, JIA Yanhui, et al. Analytic hierarchy process based on variable weights[J]. Systems Engineering- Theory & Practice, 2010(4): 723−731.

[19] Torfi F, Farahani R Z, Rezapour S. Fuzzy AHP to determine the relative weights of evaluation criteria and fuzzy TOPSIS to rank the alternatives[J]. Applied Soft Computing, 2010, 10(2): 520−528.

(编辑 杨幼平)

Application of improved AHP and group decision theory in bridge assessment

QU Bing, XIAO Rucheng, ZHONG Jian, LIN Jing

(College of Civil Engineering, Tongji University, Shanghai 200092, China)

An improved analytic hierarchy process (AHP) method based on the group decision theory was applied to bridge condition assessment for the defects in the traditional AHP. First, exponential-interval scale was introduced to establish judgment matrix whose elements were exponential-interval numbers, and an optimization algorithm of weights computing of the exponential-interval number judgment matrix was given. Then group decision theory on the basis of expert-weighting set-valued statistics was employed. The approaches of confirming expert weights concerning the judgment preference information and the aggregation of the judgment matrix were discussed, to obtain the expert-group decision matrix. Finally, a comprehensive evaluation AHP model for a certain steel box girder cable-stayed bridge was established, and the index weights were calculated, which demonstrates the feasibility and practicability of this method. The method weakens the subjective uncertainty in single-expert judgment, providing a more scientific and reliable decision-making basis for bridge maintenance and management.

analytic hierarchy process (AHP); bridge assessment; exponential-interval number; weight; group decision; set-valued statistics

10.11817/j.issn.1672-7207.2015.11.030

TU997

A

1672−7207(2015)11−4204−07

2015−01−07；

2015−03−31

国家重点基础研究发展规划(973计划)项目(2013CB036300)；国家自然科学基金资助项目(51378387) (Project(2013CB036300) supported by the National Basic Research Development Program (973 Program) of China; Project(51378387) supported by the National Natural Science Foundation of China)

屈兵，博士研究生，从事桥梁监测与状态评估研究；E-mail: bingoqu@foxmail.com