随机车流作用下悬索桥钢桥面板疲劳损伤与寿命评估

鲁乃唯，刘扬，邓扬



随机车流作用下悬索桥钢桥面板疲劳损伤与寿命评估

鲁乃唯1, 2，刘扬2，邓扬2

(1. 东南大学 土木工程学院，江苏 南京，210096；2. 长沙理工大学 土木与建筑学院，湖南 长沙，410114)

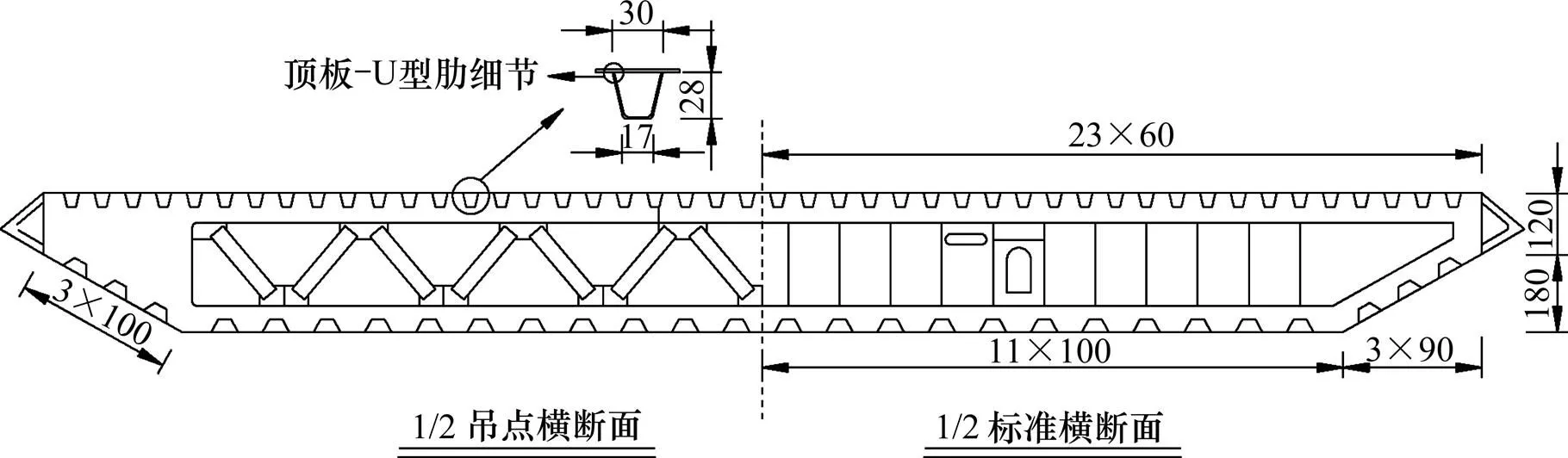
为了评估大跨度悬索桥钢桥面板在车流荷载作用下疲劳安全性，在实测车流数据的基础上，采用有限元数值模拟方法对某主跨为820 m的悬索桥钢箱梁顶板−U型肋构造细的疲劳损伤及寿命进行研究。通过对动态称重(WIM)实测车流数据的统计分析建立随机车流模型，基于应力−寿命(−)曲线和线性累积损伤准则分析运营状态和交通量增长对悬索桥钢桥面板构造细节疲劳损伤及寿命的影响。研究结果表明：随着密集运行车辆占有率的增加，疲劳损伤呈较缓增长趋势；随着交通量系数的增长，疲劳损伤呈加速增长趋势。与密集运行车辆占有率相比，交通量增长系数对疲劳损伤有较大的影响。在交通量增长系数达到6%时，钢桥面板细节疲劳寿命小于设计基准期，基于实测车流数据的疲劳性能评估对确保钢桥面板在运营期的安全性尤为重要。

钢桥面板；累积损伤；疲劳寿命；随机车流

大跨度斜拉桥和悬索桥一般采用具有较好抗风性能的流线型扁平钢箱梁结构，其正交异性桥面板在车辆荷载的反复作用下低于极限拉伸强度时会出现疲劳裂纹的萌生和扩展，达到一定程度之后即会突然断裂。针对这一问题，国内外学者通过数值模拟和模型试验等方式对其疲劳破坏模式、疲劳损伤演化机理及疲劳可靠度等方面进行深入的研究[1−3]。钢结构疲劳分析的基础是获取疲劳应力谱，其方法有基于有限元的数值模拟方法和基于长期健康监测的状态评估方法。叶华文等[4]通过对重庆两江大桥正交异性桥面板细节的足尺模型试验和有限元模拟分析研究了面内和面外荷载对桥面板寿命损伤的影响。郭彤等[5]基于应力−寿命(−)曲线法和长期健康监测数据对润扬长江大桥钢箱梁的顶板−U型肋细节疲劳寿命进行了评估。Zhang等[6]基于数值模拟方法对考虑车速和路面平整度的既有钢板桥的疲劳可靠度进行了评估，认为车速和路面平整度对疲劳损伤有较大的影响。Guo等[7]通过健康监测系统(SHM)采用的车辆数据加载到随机有限元分析中，得出了数值模拟方法与基于SHM实测应力统计分析方法得出的损伤值相同的结论。上述研究为基于数值模拟的疲劳寿命评估提供了有利条件。基于SHM系统提取的应力数据可对结构疲劳性能做出准确的评估，由于经济原因，既有桥梁很少安装该系统。而基于数值模拟方法对该类桥梁的疲劳性能评估有更好的适用性。目前主要采用疲劳荷载谱加载的方式获取结构应力谱[8]，该方法无法真实反映实际交通荷载情况。基于交通量统计的随机车流方法能够考虑实际车辆荷载的统计特征[9]，如车型、车质量、车速、行车间距及日交通量等，可应用于桥梁结构应力谱的提取及疲劳性能评估中。本文作者拟在某悬索桥动态称重(WIM)系统的基础上建立随机车流模型，采用数值模拟方法获取稀疏和密集运营状态下悬索桥钢箱梁细节的疲劳应力循环，基于−曲线和线性累积损伤准则对考虑交通量增长的悬索桥钢箱梁构造细节疲劳损伤及疲劳寿命进行分析。

1 车流作用下钢箱梁细节疲劳损伤的数学模型

钢结构疲劳损伤的分析方法主要有基于−曲线和Palmgren−Miner线性累积损伤准则方法(−曲线法)和基于Paris裂纹扩展模型的线弹性断裂力学法(LEFM方法)[10]。其中，Palmgren−Miner线性累积损伤理论认为，结构的总疲劳损伤是由变幅应力循环所造成疲劳损伤的线性叠加：

式中：n为应力循环数；N为−曲线中常幅应力幅值为S的应力总循环数。随机车流作用下钢箱梁的应力循环幅值具有变幅和高频特征，不能直接应用式(2)所示的−曲线方程反映应力幅值和应力循环数的 关系。

式中：为应力幅值；为当应力幅值为时对应的应力循环数；为材料性能参数；为−曲线图中lg和lg曲线的反斜率。Eurocode 3(EC3)规范[11]通过疲劳细节和疲劳应力幅值的详细分类，给出了式(2)中的和。

由于正交异性桥面板的应力循环中大部分应力均小于常幅疲劳极限∆D[12]，须将变幅应力循环采用根据疲劳损伤等价原则转换为等效应力循环后即可解决上述问题。EC3规范中顶板−U型肋(细节编号为50)的常幅疲劳极限∆D＝37 MPa。根据该规范将变幅应力循环等效为小于常幅疲劳极限∆D的等效常幅应力幅值eq为：

式中：S和n分别为应力谱中大于常幅疲劳极限∆D的应力幅值和对应的循环数；S和n分别为应力谱中小于∆D的应力幅值和对应的循环数；C和D分别为应力幅值大于和小于∆D的疲劳强度系数；d为日循环数。

为了考虑车辆的不同运行状态以及交通量增长对疲劳损伤的影响，根据车辆的行驶间距将桥梁的运营状态分为一般运营状态和密集运营状态。则考虑不同运营状态的结构损伤函数为

式中：为单日密集运行车辆占单日车辆的比例；为交通量增长系数；为密集运营状态下桥梁构造细节的等效应力幅值；为稀疏运营状态下桥梁构造细节的等效应力幅值。

根据上述疲劳损伤数学模型的建立过程，本文将车流作用下钢箱梁细节损伤及寿命评估分析流程划分为以下3个子步骤：基于有限元的应力时程分析、提取疲劳应力数据和疲劳寿命评估，如图1所示。

图1 车流作用下桥梁构造细节的疲劳寿命分析流程

2 随机车流作用下悬索桥疲劳应力统计分析

2.1 工程背景

某单跨钢箱梁悬索桥主跨=820 m，主缆横桥向中心间距为29.1 m，钢箱梁共65个，标准长度为12.8 m。