一组非奇异H-矩阵的实用判据

刘建州, 吕振华, 李林, 楚珊



一组非奇异H-矩阵的实用判据

刘建州, 吕振华, 李林, 楚珊

(湘潭大学数学与计算科学学院, 湖南湘潭, 411105)

运用不等式的放缩法给出了一组非奇异H-矩阵的实用判据, 改进了已有的相关结果, 并举例说明了所得结果的有效性。

非奇异H-矩阵; 不可约; 非零元素链

非奇异H-矩阵在计算数学、矩阵理论、控制论等领域有着重要的应用, 其判定问题是研究的热点问题。本文在借助判断非奇异H-矩阵一系列经典研究结果[1-7]的基础上，利用不等式的放缩法给出了一组非奇异H矩阵的实用判据, 改进了已有的相关结果, 并通过数值例子来说明其有效性。

引理1[5]若为不可约对角占优矩阵, 则。

引理2[6]若为具非零元素链对角占优矩阵, 则。

下面将给出一组判定非奇异H-矩阵的新条件, 并通过数值实例来说明其有效性。

1 非奇异H-矩阵的判定准则

本节运用不等式的放缩法给出了一组非奇异H-矩阵的实用判据, 改进了已有相关结果。

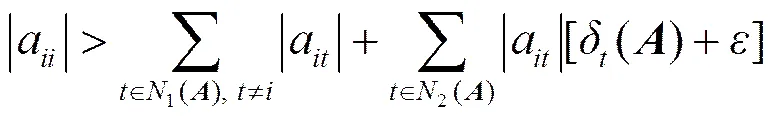
类似定理1的证法, 并结合引理1和引理2易得定理2。

2 数值例子

参考文献：

[1] 高慧敏, 陆全, 徐仲, 等. 非奇异H-矩阵的一组含参数迭代判定准则[J]. 高校应用数学学报, 2012, 27(4): 439-448.

[2] 黄廷祝. 非奇异H-矩阵的简捷判据[J]. 计算数学, 1993, 15(3): 318-328.

[3] 王洁, 刘建州, 黄泽军. 非奇异H-矩阵的一类新递进判别法[J]. 工程数学学报, 2012, 29(3): 405-412.

[4] 周伟伟, 陆全, 徐仲, 等. 非奇异H-矩阵的迭代判定准则[J]. 工程数学学报, 2013, 30(5): 715-720.

[5] Varga R S. On recurring theorems on diagonal dominance [J]. Linear Algebra Appl, 1976, 13: 1-9.

[6] Gan T B, Huang T Z. Simple criteria for nonsingular H-matrices [J]. Linear Algebra Appl, 2003, 374: 317-326.

[7] Farid F O. Notes on matrices with diagonally dominant properties [J]. Linear Algebra Appl, 2011, 435: 2 793-2 812.

(责任编校:刘晓霞)

A set of practical criteria for identifying nonsingular H-matrices

Liu Jianzhou, Lv Zhenhua, Li Lin, Chu Shan

(Department of Mathematics and Computational Science, Xiangtan University, Xiangtan 411105, China)

A set of practical criteria for judging nonsingular H-matrices is obtained by applying the techniques of inequalities, which improves the existing and related results. The effectiveness of the proposed results are illustrated by a numerical example.

nonsingular H-matrix; irreducibility; non-zero elements chain

10.3969/j.issn.1672–6146.2015.02.002

O 151.21

1672–6146(2015)02–0003–02

刘建州, liujz@xtu.edu.cn.

2014-10-24

湖南省教育厅重点项目(12A137); 湖南省研究生科研创新项目(CX2014B254)。