双权重应急交通网络最优路径数学模型及算法研究
盖文妹,邓云峰,蒋仲安,李竞,杜焱
双权重应急交通网络最优路径数学模型及算法研究
盖文妹1, 2, 3,邓云峰2,蒋仲安1,李竞3,杜焱1
(1. 北京科技大学土木与环境工程学院,北京,100083;2. 国家行政学院,北京,100089;3. 中国安全生产科学研究院公共安全研究所,北京,100012)
运用运筹学中的图论与多目标优化理论和方法建立双权重应急交通网络最优路径的数学模型,基于超启发式算法思想,提出适合该模型的双试探点搜索算法。算法从应急决策的角度寻找最优路径,通过操纵和管理低层启发式算法,不断获得新启发式算法,是一种快速、近似的算法。用真实路网验证本文算法在应急管理与决策中的应用效果,并与A*算法进行对比分析,证明前者在双权重应急交通网络的路径寻优上更具优势。此外,用随机路网测试不同限制条件参数和以及节点规模,研究算法精度参数1及2对双试探点搜索算法求解效率的影响。研究结果表明:所提出的算法求解效率与及算法流程参数1和2有显著的正相关关系,而与限制条件参数和之间的相关性并不显著,算法有较高的求解效率,为突发事件救灾与疏散提供了有力的技术支持。
应急管理;路径选择;双权重网络;优化模型;超启发式算法
在我国,自然灾害、事故灾难、公共卫生和社会安全等突发事件时有发生。一旦发生此类事件,在应急管理与处置过程中一个重要环节就是制定出救灾、避灾、物资运输与调度等的最佳路线。从图论角度来看,灾变条件下地面互相交错的道路或井下错综复杂的巷道实际上是一个连接的网络图,路段或巷道为图的边,路段或巷道之间的交点抽象成图的顶点,权则是与应急交通网络中有向边相关的数量指标,如路段或巷道的长度、风险等级、通行时间、经济成本等,根据应急决策的优化目标赋予边相应的权重。传统的路径选择研究集中在单一权重交通网络,路径优化问题可以转化为图论中的最短路问题,可借助传统最短路算法实现,如Dijkstra算法、A*算法和Floyd算法等[1−2]。但应急交通网络的边往往与多个评价标准相关,属于多权重网络图,此时的最优路径问题实际上属于多目标最短路问题,无法直接由传统最短路模型计算。由于路径的各个优化目标之间通常存在冲突,某个目标下的最优解对于另一个目标可能并非最优,因此,多目标最短路问题一般没有绝对的最优解,而是一个有效解集,因而增加了求解难度[3]。双目标最短路问题是多目标最短路问题中的一个常见情况,Handler等[4]证明了该问题是非确定性多项式(NP)完全问题。Hansen等[5−6]对如何获得双目标最短路的有效路径进行了研究,获得了所有的有效路径的集合,但算法的复杂性较高。近年来,随着智能计算领域的发展,出现了一种超启发式算法。该算法提供了某种高层策略,通过操纵或管理一组低层启发式算法(LLH),以获得新启发式算法。这些新启发式算法则被运用于求解各类NP-难解问题。超启发式算法与启发式算法都是运行在搜索空间上,但是各自的搜索空间构成不同:传统启发式算法是工作在由问题实例的解构成的搜索空间上;而超启发式算法运行在一个由启发式算法构成的搜索空间上,该搜索空间上的每一个顶点代表一系列LLH的组合[7]。本文作者基于运筹学中的多目标优化理论和方法建立一种双权重应急交通网络最优路径模型,并基于超启发式算法思想从应急决策的角度降低计算复杂性,提出一种快速求解模型的近似、快速算法。
1 双权重应急交通网络最优路径的数学模型
1.1 问题描述
近年来,重大事故及自然灾害对人类社会造成的损失不断加剧,如江西省新余市庙上煤矿“1·8”重大火灾事故、“12·23”重庆天然气井喷事故、“5·12”汶川特大地震及“7·21”北京特大暴雨等[8−9]。一般抢险救灾的首要任务是撤退灾区人员,而选择最佳救灾与避灾路线往往是一件比较棘手的工作[10−11]。在国内外事故灾害中,常因路线的选择失误而产生重大人员伤亡事故。此外,当抢险救灾周期较长时,还需对受灾地点紧急运送救援物资,保证灾区群众的正常生活,此时物资运输调度路线的选择也是决策者急需解决的问题[12−13]。研究最佳疏散路线、最佳救灾路线及救灾物资的最佳调度路线等最优路径选择问题,对确保最大限度地减轻事故灾害造成的损失、各项救灾装备及人力的有效运用有重要意义。运用运筹学中图论的理论和方法,本文作者研究的应急交通网络路径优化问题可以描述为:对于网络图=(,)(其中,={v}是图的节点集,={(v,v)|v,v∈N}是图的边集,||=,||=),设1(,)和2(,)为边(v,v)的2个不同的权重参数,1(,)≥0,2(,)≥0,这样把1个应急路径优化问题和1个赋双权的网络图之间建立了同构关系。由于传统的最短路算法不能直接求解双权重网络图的最短路,需根据实际问题建立合理的数学模型并设计出适合模型的算法。
1.2 模型建立
令表示1→v的1条路,双权重应急交通网络的最优路径模型(bi-weight shortest path, BWSP)可以用下述数学模型表示:
其中:1()和1()是路径的2个评价函数,评价函数的下标按照优化目标重要性降序编号。BWSP即求1→v的1条最优路径*,使其同时满足式(1)和 式(2)。
BWSP模型在应急决策中应用广泛,对于矿井火灾中的疏散人员而言,最优路径是指事故发生后供遇险人员最安全、能迅速撤离的路线[11],因此,可将风险系数和巷道长作为巷道网络的权重;对于毒气泄漏事故中的救灾人员而言,最优路径是指救灾人员从救灾基地到受灾地点的抢险救灾路线。虽然救灾人员佩戴氧气呼吸器及备用装置并经过专门的训练,可在有毒气体扩散下的路段(或巷道)上通行,但可携带氧气量有限,为了保障救灾人员的安全和救援行动的效率,可将人员的氧气消耗量和路段(巷道)的“当量长度”作为路网(或巷道网络)的权重[1]。对于应急物资的调度人员而言,最优路径是指事故发生后将应急物资从调度中心运输到受灾地点的最迅速且成本最低的路线,时间是任何紧急态势下不可忽视的决策属性,此外,在紧急态势下,由于运量大和运输时间集中等原因,常常会发生运力紧张状况,追求运输调度的经济性目标,能够有效缓解运力不足的矛盾,因此,可将物资运输时间和运输成本作为路网的权重[14]。
2 模型算法的研究
2.1 Pareto-optimal最优解意义下的最优解
对于1()和1(),实际运算中很难找到1条路径,为解决该问题首层LLH思路是在Pareto-optimal最优解意义下先找到BWSP的有效解集作为最优解的搜索空间,搜索空间中的每个有效解都是1个备选方案,在此给出如下定义[15−16]。
定义1 设1、2是1→v的2条路径,若1(1) ≤1(2),2(1)≤2(2),且至少有1个是严格不等式,则称在Pareto-optimal最优解意义下,1有效于2。
定义2 设*是1→v的1条路径,若不存在1条路有效于*,则*称为有效解。
令表示所有有效解的集合,若能求得,决策者则可根据需要从中选择符合需要的最优路径,但是实现这一思路的算法复杂性较高[5−6],往往无法满足应急决策的需求。对于应急决策者而言,并不是一定需要获得所有的有效解,而希望对每个决策目标均会有一定的限制,使所求得的最优路径能在预期达到的程度范围内。据此,新的LLH思路是为1()和2()分别设定一个决策者可以接受的上限Z1和Z2,并假定min1()为决策者首要关注的目标,2()为决策者需要控制的评价函数,然后从决策者的角度寻找的1个子集,={|1()≤Z1,2()≤Z2},在集合中寻找满足决策需要的最优路径。因此,BWSP绝对有效解可定义为:
定义3 设为1→v的有效解的集合,**是1→v的1条路径,若2(**)≤Z2,1(**)=min1() ≤Z1,∈,则称**绝对有效解。
2.2 构造等效单权重应急交通网络图
绝对有效解**就是应急决策者需要的最优路径,但在具体进行计算之前,决策者往往很难确定一个较为准确的上限值。此时新的LLH思路是:采用加权平均结构构造一个新的权重参数,将双权重应急交通网络转换为等效的单权重网络。这样不仅可以实现经典最短路算法的调用,而且可间接得到与评价函数相关的2个辅助决策函数,据此可设置2个评价函数的上限值。加权平均法[17]是平衡2个目标函数之间“利益”的一种常用的方法,在此利用算数加权结构为边(v,v)构造1个新的权重参数,即(,) =∙1(,)/(+)+∙2(,)/(+) ,其中≥0,≥0,且+>0,并建立如下辅助函数:
P,β表示1→v的1条路径。通过对边的2个不同的权重进行线性加权,将双权重应急交通网络转换为等效的单权重网络,满足式(3)的路径P,β实际是该单权重网络最短路,可采用经典最短路算法求解,其中Dijkstra算法和A*算法是计算1个源节点到其他节点的单权最短代价路径的最快的2种算法,二者本质上相同,唯一区别是前者没有启发式而在各个方向上平均搜索,在找到目标前通常会探索更大的区域,所以一般会比后者更慢一些。但有时并不知道目标节点的位置,比如事故发生后可能有若干安全区域,要想让避灾人员去最近的那个,在这种情况下,Dijkstra算法就比A*更适合,因为不知道哪个更近;若用A*算法,唯一的选择是依次计算每个目标许路的“长度”,然后选择最近的路径[18]。因此,若目标节点有多个时,则选择Dijkstra算法求解P,β,否则选择A*算法。
定理 设P,β为1→v的满足式(3)的1条路,则P,β为BWSP的1个有效解。
证明 假设P,β不是BWSP的1个有效解,则必然存在路径使得1()≤1(P, β),2()≤2(P, β),且至少有1个是严格不等式,即≤,≤。又因为≥0,≥0,且+>0,故≤,≤,且其中至少有1个是严格不等式,故<,即≤,这显然与式(3)矛盾,因此,假设不成立,原命题得证。
根据上述定理可知:利用式(3)求解等效单权重网络最短可间接获得BWSP的有效解集。令=/(+),则/(+)=1−,且0≤≤1,则式(3)可转化为关于的函数表达式=()。对于∀∈[0,1],若存在满足式(3)的1→v的1条路P,则对应得到2个评价函数值1(P)和2(P),因此,1(P)和2(P)实际上是关于的函数,记作1(P)=1()和2(P)=2(),并有如下性质成立:
性质1 当2()递增时1()递减,当=1时1()最小,当=0时2()最小。
证明 任取1∈[0,1],2∈[0,1],且1<2。设1和2是分别对应于加权系数1和2的满足式(3)的2条路,根据式(3)显然有:
故1∙(−+(1−1)∙(−≤0;2∙(−+(1−2)∙(−≥0。
因为1≥0,2≥0,故≥;≤。
即1(1)≥1(2),2(1)≤2(2)。故当递增时,1() 递减,2() 递增。若=/(+)=1,则/(+)=0,(,)=1(,)。设1为此时满足式(3)的1条路,则1也满足式(1)。显然,1(1)=1(1)=min1()=min1()。同理可证明2(0) =min2()。
设1()≤Z1的解集1={|a≤≤1},2()≤Z2的解集2={|0≤≤b},a,1及0分别为=a,=1及=0时满足式(3)的路径,令集合=1∩2,取遍时求得的满足式(3)的所有路径即为备选路径的集合,那么,容易证明辅助函数有下面性质成立:
性质2 若2(0)>Z2或1(1)>Z1或b<a,则=Ø,**无解;若≠Ø:若2(1)≤Z2,则**=1;若2(a)=Z2,则**=a;否则b∈(a,1)。
证明 根据性质1可知:2(0) =2(0) =min2(),1(1)=1(1)= min1();根据定义3可知:若f(0)>Z2或1(1)>Z1,则min2()>Z2或min1()>Z1,则1=Ø或2=Ø,故=Ø;若b<a,则=Ø。因为=Ø,故=Ø,**无解。若≠Ø,根据定义3可知:若f(1)≤Z2,由性质1,1(1) =1(1)=min1()≤Z1,故={1},**=1;若2(a)=Z2,则2={|0≤≤a},故={a},**=a;否则a<b<1,命题得证。
令在[0,1]内依次取值,每次增加1/(其中,为正整数),求满足公式(3)的路径,并计算该路径对应的2个评价函数值,可获得2条函数曲线,曲线上每1个观测值均对应BSWP的1个有效解,如图1所示,据此决策者很容易为2个决策目标确定一个较为合理的上限Z1和Z2。根据性质2可知:决策者设置的限制条件不同,**的结果不同。从图1可以看出:当Z1和Z2应分别在[1(1),1(0)] 和[2(0),2(1)]范围内合理取值,当且仅当a≤b时,**有解,且=[a,b],当取遍集合时求得的所有路径的集合便是的子集;若a<b,则可能∃*∈(a,1),满足=*时根据式(3)求得最优路径**。
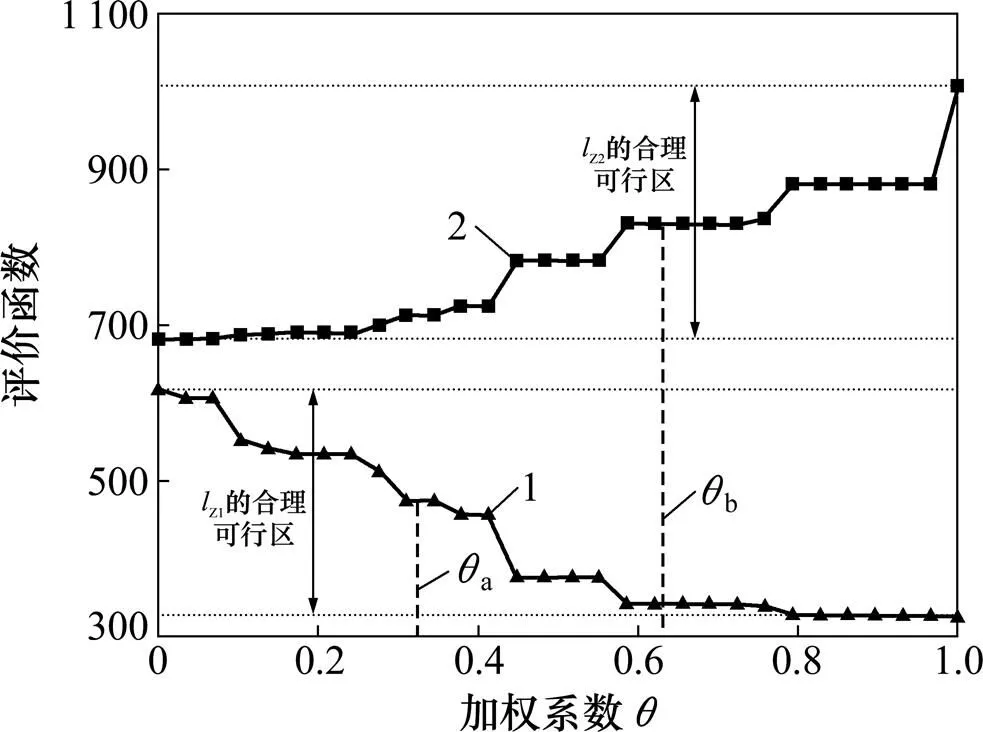
1—f1;2—f2
显然,当前新的LLH思路是如何寻找1个*,当=*使P在满足限制条件1(P)≤Z1及2(P)≤Z2的同时,使首要评价函数1(P)达到最优。本文将在下面证明:若*存在,则可以通过不断缩减区间的方法求出,并据此得到最优路径**,然后在算法可行的基础上给出具体的编译方法。
2.3 算法可行性分析及编译方法
缩减区间法是一种典型的一维搜索算法,有较高的求解效率[19]。为了证明区间缩减算法的可行性,首先引入辅助函数的另外2个性质:
性质3 令P表示对应于加权系数的满足式(3)的1条路径,,∈[,]⊂[0,1],且<。那么,
1) 若1()>Z1,则1(P)>Z1,∀∈[]。
2) 若1()<Z1,则1(P)<Z1,∀∈[,]。
3) 若(1()−Z1)(1()−Z1)<0,则1(P)<Z1与1(P)>Z1至少有1个成立,∀∈[,]∪[,]。
4) 若1()=Z1,则a;如果1() =Z1,则a。
性质4令P表示对应于加权系数的满足式(3)的1条路径,,∈[,]⊂[a,1],且<。那么:
1) 若2()
2) 若2()>Z2,则1(P)≤1(P)且2(P)>Z2,∀∈[,]。
3) 若(2()−Z2)(2()−Z2)<0,则1(P)≥1(P)与2(P)>Z2至少有一个成立,∀∈[,]∪[,]。
4) 若2()=Z2,则**=P;若2() =Z2,则**=P。
结合性质1和图1,容易证明性质3和性质4成立。不妨假设在=a时使得2()=Z2,=*时求得的满足式(3)的路径绝对有效解**。若a∈[,] ⊂[0,1],根据性质3,只需在[,]上取2个点和,通过比较1()和1()与Z1之间的关系,可以去掉部分搜索区间[,](见图2(a))。若*∈[,]⊂[a,1],根据性质4,同样只需在[,]上取2个点和,通过比较2()和2()与Z2之间的关系,可以去掉部分搜索区间[,](见图2(c))。图2所示为根据性质3和性质4求解**时所有去掉区间的示意图。因此通过不断缩减区间的方式,可以最终求得a,进而求得**。
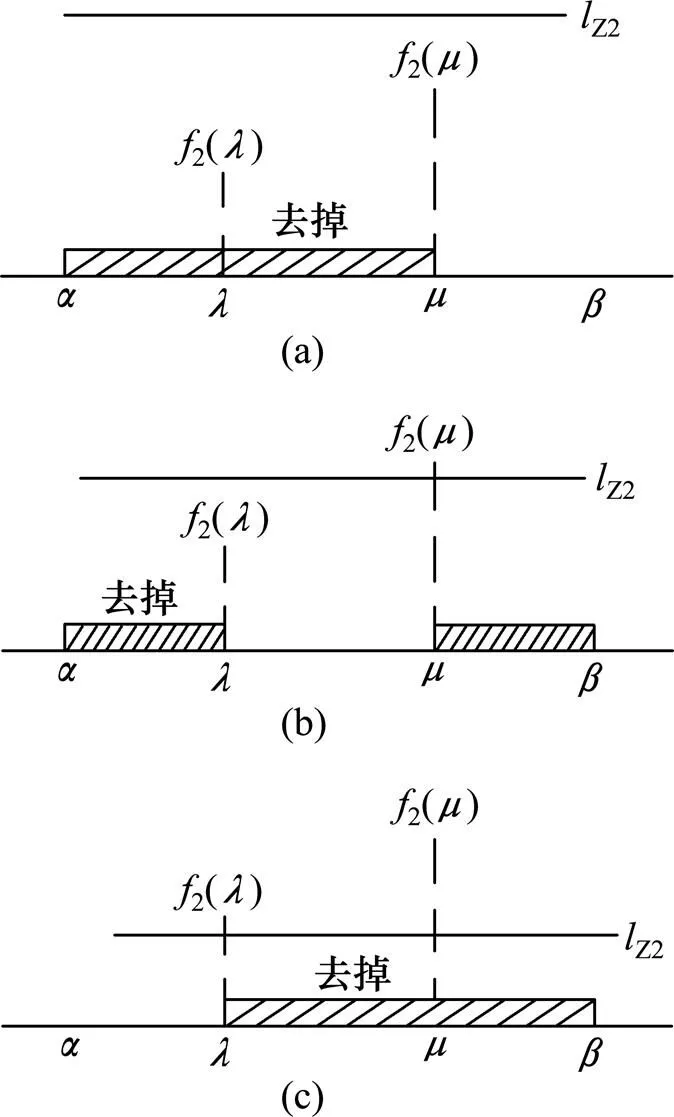
(a) 去掉区间[α, μ];(b) 去掉区间[α,λ];(c) 去掉区间[λ,β]
综上可知:通过区间缩减的方法寻找**具备可行性。按照这一思想构造算法,很自然地希望在比较2个函数值与上限值之间的关系后去掉的区间在任何情况下都大,在此令[,]=[,]+[,]=[,],可见和实际是[,]的2个3等分点。以经典最短路算法为底层算法,设计基于双试探点的区间缩减搜索算法,算法程序分为2个阶段,分别如图3(a)和3(b)所示,其中1和2分别表示a和*的精度,1>0,2>0。利用该算法,通过不断搜索,或者恰好在=*处获得绝对有效解**,或者最终得到1个较小的*的近似区间[α,β],并在=α处获得绝对有效解**的1个近似解,记作app。
因此在驾驶时实现调整智能自动化技术能够加强车辆控制和机车运转状态的监控与调整,让驾驶人员更容易的能够及时知道机车及时的运转状态,预防危险状况的出现。结合科学技术调控系统,设定对车辆水箱内的降温水温度范围的严格调控,如果超过或少于设定的调控范围,便将会发起自我保护信号并及时进行系统调控,与此同时还会有警报来提醒驾驶员注意。至于刹车问题的解决方案,对不同的路面状况,计算机系统将运转信息回馈至中心调控处理体系,体系通过对状况的精准判定作出精确的预算。在人工智能的协助下,还可能给司机行驶意见,规划更为安全的路径。

(a) 第1子程序;(b) 第2子程序
2.4 算法误差、时间复杂度及优势分析
假定BWSP的绝对有效解**存在,且可在=*处获得,则2(*)=Z2,2(**)=1(*)。若图3(a)所示算法迭代1次,图3(b)所示算法迭代2次后得到最优解的1个近似解app,显然,此时算法的误差无法预先精确计算得到。从图1可以看出:1()和2()的曲线接近线性变化,因此,对误差的推理采用线性估计:,;由图3(a)可知:每一次迭代中β在当前搜索区间的哪个3等分点处获得,不妨假定为左侧3等分点,则,所以。令=(Z2−2(0))/(2(1)−2(0)),则1(*)=1(1)+(1−) (1(0)−1(1)),
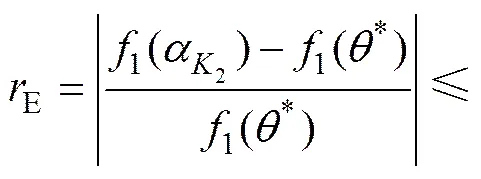
其中:E为相对误差;=1(0)/1(1)≥1。由式(4)可知:算法具备收敛性。
对于非负带权图而言,Dijkstra单源最短路径算法的时间复杂度为(+lg),A*单源最短路径算法的时间复杂度为(lgC),C为CLOSE表中的节点 数[20]。由图3所示算法流程,本文作者搜索算法的单源最优路径的时间复杂度为(∙)。其中,以Dijkstra算法作为底层算法时,=+lg;以A*算法作为底层算法时,=O∙lgC;O为目标节点的数量;为算法结束时底层算法调用次数计数器的值。
对于确定的源节点和目标节点,本文算法是通过在一系列LLH构成的搜索空间上缩小区间的方式不断逼近绝对有效解,而不是在各个方向上平均搜索,因此,算法求解效率较高。算法在缩减区间寻找最优解时采用双试探点而不是单一试探点,有效避免了极端情况对算法求解效率的影响。如果采用单试探点搜索,由于无法预知最优解靠近搜索区间的哪一个端点,算法可能恰好选择了靠近另一个端点的试探点进行搜索而使算法迭代次数增加。此外,本文提出的算法不仅利于应急决策者解决问题,而且可以作为决策者提出问题提供辅助工具。当已知需要优化的2个决策目标及其限制条件时,决策者可以利用本文的搜索算法求得符合限制条件的一系列绝对有效解的采样值,决策者可以选择根据算法求出的绝对有效路径作为应急路线,也可以设定合理的最优解(绝对有效路径)邻域[21],根据实际情况将该范围内的采样值择优设定为应急路线,即应急路径优化问题的解决。同时,若已知需要优化的2个决策目标,但其限制条件未知,利用该算法可以获得2个评价函数关于权系数的趋势曲线,根据2条曲线,决策者可以根据需要为某一评价函数的决策目标设置不同的限值条件,形成不同的优化问题即问题的提出。
3 算例模拟与结果分析
假设现有一批救援物资需要从调度中心运往受灾地点,将紧急救援物资调度中心所在地1到物资需求点v之间纵横交错的道路定义为1张网络图,应急救援物资运输线路的选择既要考虑应急条件下物资运送的时效性,又要最大限度地降低运输费用,但相对于时效性经济性因素重要性较低,故将运输时间作为首要优化目标,运输成本为次要优化目标。所要求解的应急救援物资最佳运送路线问题属于确定的源节点和目标节点之间的路线选择问题,为缩小算法运算过程中探索的区域,故底层算法采用A*算法。表示算法总迭代次数,=1+2(其中1和2取决于迭代计数器,为A*算法调用总次数)。
3.1 应用效果分析
测试网络选择真实路网,模拟中路段运输时间根据路长、交通工具的种类按照平均行驶速度计算;路段运输成本为随机假定设置,在实际情况中,路段运输成本不仅与运输距离有关,而且受到可用交通工具的种类以及道路收费标准等诸多因素的影响,如当运输距离一定时,采用汽车运输比采用火车运输的方式应急物资的运输成本要低,因此,运输成本并不与运输时间成正比,需要根据实地调研获得;假定Z1=200 min,Z2=1 500元,利用A*算法可直接求解1→n的运输时间最短路1或运输成本最短路2;令12表示1→v的运输时间和运输成本的双权重最短路,编译并运行本文的双试探点搜索算法求解。在10 000个节点地图上求解1,2和12,如图4所示,地图数据采用MapInfo MIF数据格式。双试探点搜索算法与A*算法计算结果对比如表1所示。从表1可以看出:根据A*算法求解的2条最优路径中,1的运输时间最短。这虽然满足了应急救援物资运输的时效性需求,但总运输成本较大,超过了经济上可承受的范围,不利于缓解运力紧张的实际状况。2的运输成本最少,但是运输时间超出可承受的上限Z1,从应急救援物资运输的时效性来看并不合理。根据本文搜索算法求解的路径12,其运输成本相比路径1少1 384元,却只比1的运输时间多12 min;12的运输时间相比路径2少109 min,却只比2的运输成本多58元。从救援物资运输的时效性考虑,12 min的优势对于运输时间的降低并不明显;从路线的经济性考虑,58元的优势对于运输成本的降低并不明显,据此可以得出结论:同时兼顾时效性和经济性目标方面,本文的双试探点搜索算法比传统的最短路算法更具优势。
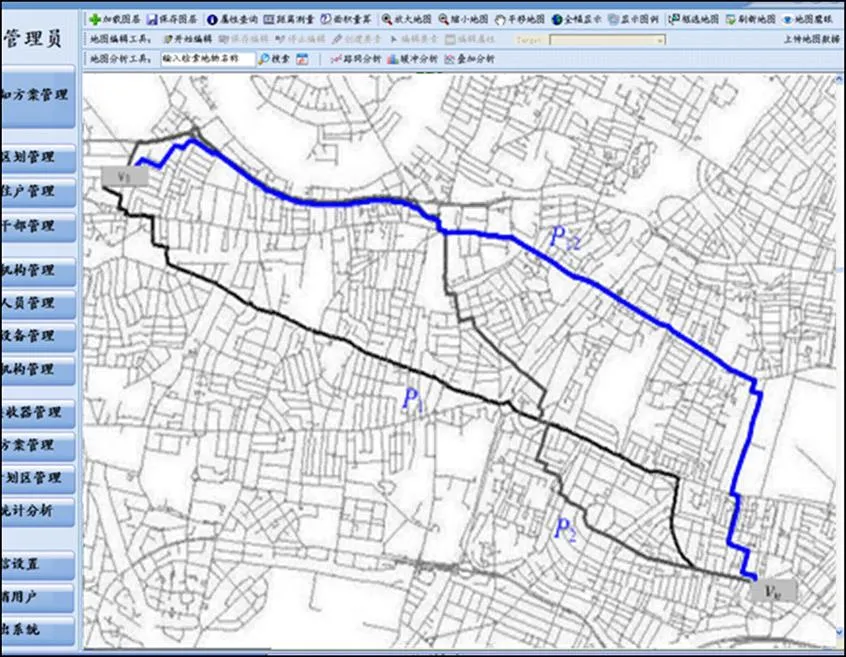
图4 真实路网最优路径计算
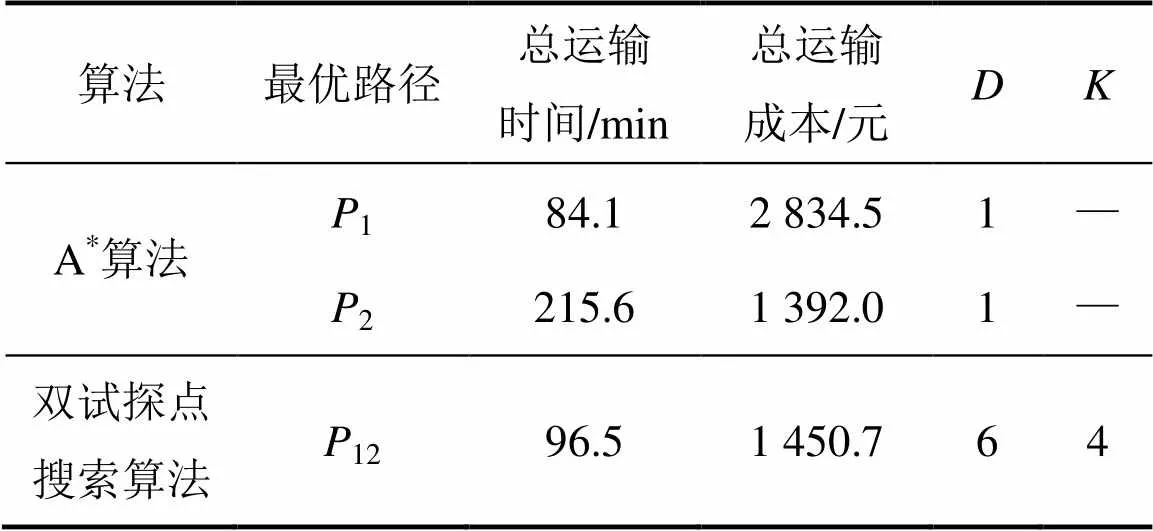
表1 双试探点搜索算法与A*算法计算结果对比
3.2 算法求解效率
调用Python平台中的NetworkX包[22],采用grid_2d_graph(,, periodic=False, create_using=None)方法生成1个节点规模=×的随机路网,作为本次模拟的测试网络,如图5所示。2种权重参数仍为假定设置,限制条件保持不变。令=(Z1−1(1))/(1(0)−1(1)),=(Z2−2(0))/(2(1)−2(0))。测试目标是研究不同限制条件参数和,节点规模,算法精度参数1及2对算法求解效率的影响。

图5 400节点的随机路网
图6所示为迭代次数与参数和及节点规模之间的关系。利用Pearson相关系数[23]研究不同参数与迭代次数之间的线性关系,统计结果见表2。结合图6和表2可以看出:算法阶段2的迭代次数2与参数相关性显著,且2与正相关。但从图6 (b)可知:2受参数的影响程度并不大;2与参数的相关性则并不显著。除此之外,算法迭代次数的其他指标和和1与参数和不具备显著相关性,这主要由于算法采用2个3等分点作为试探点,实质上是从搜索区间的2个相反方向同等速度地向中间进行搜索,从而减弱了Z1或Z2的变化对算法搜索速度的影响,这种设计优于单试探点搜索,因为当a或*存在极端情况而极为靠近搜索区间某1个端点时,采用单试探点沿着另外1个端点向该端点靠近的方向搜索时,会使迭代次数大大增加,从而导致求解效率降低。算法总迭代次数的所有指标,,1和2与节点规模均具备显著相关性,且均为正相关关系,这说明随着节点规模的增加,算法求解效率降低。因此,当在大地图上有大量对象在寻路时,算法的时间复杂度增加,建议采用本文作者算法时应尽量使用更小的地图或者更少的寻路者。通过反复测试发现,即使对于10 000节点的随机路网,双试探点搜索算法=15和=28即获得双权重最优路径,表明本文作者算法求解效率较高。表3所示为迭代次数与精度参数1和2之间的关系。1和2与算法终止条件有关。分析表3可知:1(2)越小,1(2)随之增大,导致和增加;当1(2)过大时,会使近似解与最优解之间的误差过大;当1(2)过小时,可能已经不存在满足限制条件的更优路径,算法却仍在搜索,或者即便存在更优的路径,却对于改善应急策略作用不大,反而使得算法的迭代次数大大增加,因此,有必要合理设置算法终止条件以保证算法的精度及求解效率。
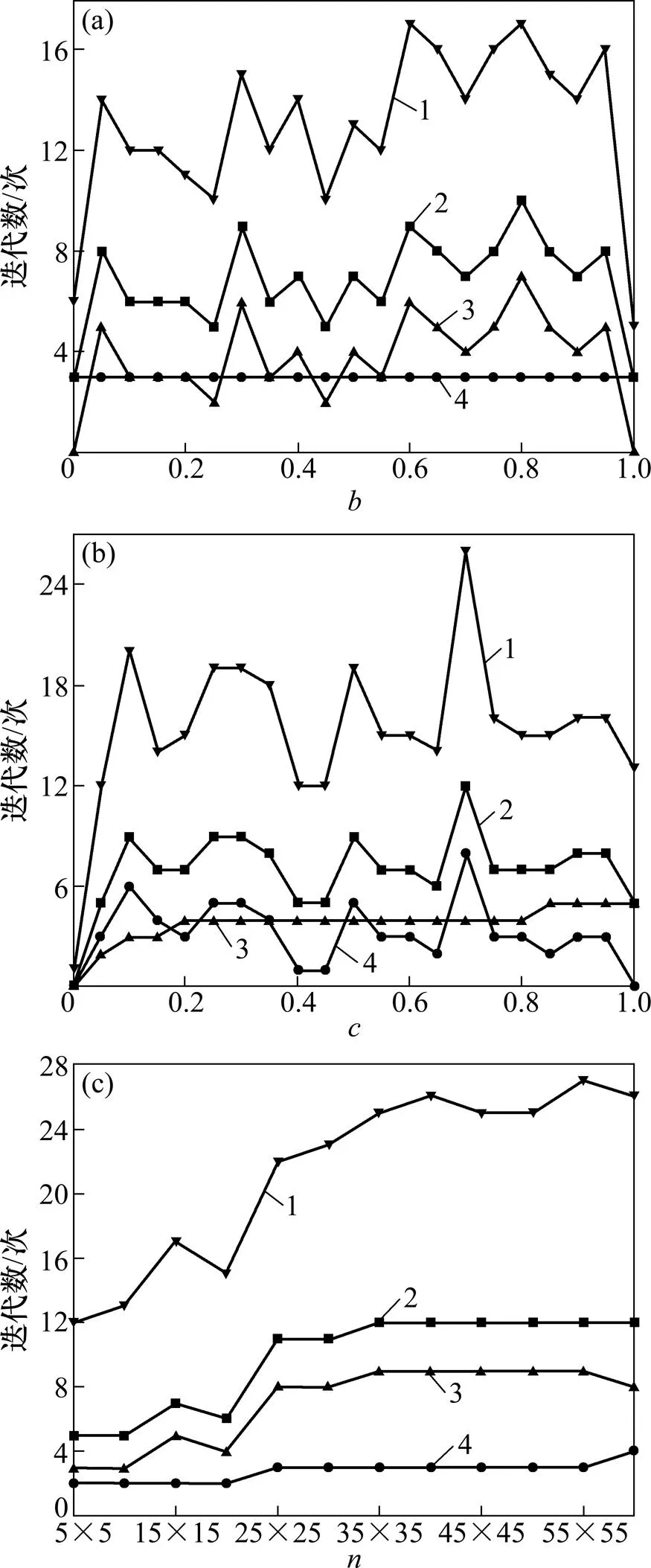
(a) 参数b;(b) 参数c;(c) 规模n
注:*表示因为至少有1个变量为常量,所以无法进行计算;**表示在0.01 水平(双侧)上显著相关。
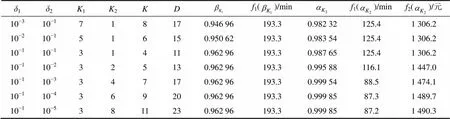
表3 迭代次数与精度参数δ1及δ2之间关系
4 结论
1) 运用运筹学中的图论及多目标优化理论及方法建立了双权重应急交通网络最优路径的数学模型,提出适合该模型的双试探点搜索算法。算法基本思路是:将经典的最短路算法作为底层算法,采用加权平均结构为模型构造新权重,将双权重应急交通网络转换为等效的单权重网络,在低层启发式思路构成的搜索空间上调用底层算法反复迭代求解等效单权重应急交通网络的最短路,在迭代中选取2个3分点作为试探点不断缩小搜索区间直至逼近最优解,不仅加权系数易于确定,而且能在较短时间内获得符合误差限值的绝对有效解。
2) 利用地理信息系统的Python控件进行程序编制,在真实路网上测试本文算法的应用效果,证明该算法在双权重应急交通网络的路径寻优上,相比A*算法在优化结果上更具优势。利用随机路网测试了不同参数对算法的求解效率的影响。本文算法不仅适用于双权重网络,也可推广到3种权重以上的应急交通网络。
3) 本文提出的算法是基于超启发式算法思想的一种近似算法,通过系列低层启发式算法获得新启发式算法,不断缩小最优解的搜索空间,不仅利于应急救援优化方案的决策者解决问题,而且可以根据算法得到辅助决策曲线图提出问题。双权重应急交通网络最优路径的确定对于重大事故及自然灾害应急救援预案的编制具有参考价值。
[1] 高蕊, 蒋仲安, 董枫, 等. 基于MapObject的矿井火灾动态最佳救灾路线数学模型和算法[J]. 北京科技大学学报, 2008, 30(7): 705−709. GAO Rui, JIANG Zhongan, DONG Feng, et al. Mathematical model and algorithm of a dynamic optimum rescue route during mine fire time based on MapObject[J]. Journal of University of Science and Technology Beijing, 2008, 30(7): 705−709.
[2] Golden B. Shortest-path algorithms: A comparison[J]. Operations Research, 1976, 24(6): 1164−1168.
[3] 郑金华. 多目标进化算法及应用[M]. 北京: 科学出版社, 2007: 2−19. ZHENG Jinhua. Multi-objective evolutionary algorithm and its application[M]. Beijing: Science Press, 2007: 2−19.
[4] Handler G Y, Zang I. A dual algorithm for the constrained shortest path problem[J]. Networks, 1980, 10(4): 293−309.
[5] Hansen P. Bicriterion path problems[C]//Multiple criteria decision making theory and application. Heidelberg, Berlin: Springer, 1980: 109−127.
[6] Climaco J C N, Martins E Q V. A bicriterion shortest path algorithm[J]. European Journal of Operational Research, 1982, 11(4): 399−404.
[7] Bai R, Blazewicz J, Burke E K, et al. A simulated annealing hyper-heuristic methodology for flexible decision support[J]. A Quarterly Journal of Operations Research, 2012, 10(1): 43−66.
[8] 刘晶, 邓云峰, 李竞. 三高气田钻完井重大事故现场监测数据采集管理系统的设计与实现[J]. 中国安全生产科学技术, 2011, 7(6): 58−62. LIU Jing, DENG Yunfeng, LI Jing. Design and implementation of the scene data acquisition and management system for major incident after logging of high risks gas field[J]. Journal of Safety Science and Technology, 2011, 7(6): 58−62.
[9] 邓云峰. 毒气泄露事故人员疏散模型及应用研究[D]. 北京: 北京科技大学土木与环境工程学院, 2008: 1−38. DENG Yunfeng. Study on pedestrian evacuation model for accident releasing toxic vapors[D]. Beijing: University of Science and Technology Beijing. School of Environment and Civil Engineering, 2008: 1−38.
[10] 余为波, 吴晓光, 王涛, 等. 基于最短路径算法的舰船通道逃逸路线研究[J]. 中国舰船研究, 2008, 3(2): 16−20. YU Weibo, WU Xiaoguang, WANG Tao, et al. Research on the evacuation route of passage in ship based on shortest paths algorithm[J]. Chinese Journal of Ship Research, 2008, 3(2): 16−20.
[11] 肖国清, 温丽敏, 陈宝智, 等. 毒气泄漏时的最佳疏散路径[J]. 东北大学学报(自然科学版), 2001, 22(6): 674−677. XIAO Guoqing, WEN Limin, CHEN Baozhi, et al. Shortest evacuation route on toxic leakage[J]. Journal of Northeastern University (Natural Science), 2001, 22(6): 674−677.
[12] 龚亚伟. 应急救灾物资车辆最优路径选择的研究与实现[D]. 武昌: 武汉理工大学物流工程学院, 2008: 5−34. GONG Yawei. Research and Implementation of optimal path for emergency relief goods vehicles[D]. Wuchang: Wuhan University of Technology. School of Logistics Engineering, 2008: 5−34.
[13] 李永义, 李伯权, 储浩. 交通生命线系统震后应急调度模型及方法[J]. 南京工业大学学报(自然科学版), 2011, 33(1): 33−36. LI Yongyi, LI Boquan, CHU Hao. Emergency scheduling model and its method of traffic lifeline system after earthquake[J]. Journal of Nanjing University of Technology (Natural Science Edition), 2011, 33(1): 33−36.
[14] 张毅, 郭晓汾, 王笑风. 应急救援物资车辆运输线路的选择[J]. 安全与环境学报, 2006, 6(3): 51−53. ZHANG Yi, GUO Xiaopan, WANG Xiaofeng. Route choice for transporting emergency succor materials[J]. Journal of Safety and Environment, 2006, 6(3): 51−53.
[15] 李帮义, 姚恩瑜. 关于最短路问题的一个双目标优化问题[J]. 运筹学学报, 2001, 5(4): 67−71. LI Bangyi, YAO Enyu. A two objective reoptimization problem about node and arc[J]. Operations Research Transactions, 2001, 5(4): 67−71.
[16] 魏航, 蒲云, 李军. 一种求解双目标最短路的方法[J]. 系统工程, 2005, 23(7): 113−117. WEI Hang, PU Yun, LI Jun. An approach to biobjective shortest path[J]. Systems Engineering, 2005, 23(7): 113−117.
[17] 李大矛. 平均值的高斯特征与比较研究[M]. 长春: 吉林大学出版社, 2012: 1−13. LI Damao. Mean Gaussian characteristics and comparative study[M]. Changchun: Jilin University Press, 2012: 1−13.
[18] Golden B. Shortest-path algorithms: A comparison[J]. Operations Research, 1976, 24(6): 1164−1168.
[19] 吴祈宗, 侯福均. 运筹学与最优化方法[M]. 北京: 机械工业出版社, 2013: 105−109. WU Qizong, HOU Fujun. Operations research and optimization methods[M]. Beijing: Mechanical Industry Press, 2013: 105−109.
[20] Pokorny K L, Vincent R E. Multiple constraint satisfaction problems using the A-star (A*) search algorithm: Classroom scheduling with preferences[J]. Journal of Computing Sciences in Colleges, 2013, 28(5): 152−159.
[21] 张振坤. 网络最短路的解集结构及有关问题[D]. 郑州: 郑州大学数学与统计学院, 2002: 10−17. ZHANG Zhenkun. Solution set of network shortest and related problems[D] Zhengzhou: Zhengzhou University. School of Mathematics and Statistics, 2002: 10−17.
[22] Hagberg A, Schult D, Swart P. NetworkX Tutorial[EB/OL]. [2012−07−04]. http://networkx.lanl.gov/networkx_tutorial.pdf
[23] 谢龙汉, 尚涛. SPSS 统计分析与数据挖掘[M]. 北京: 电子工业出版社, 2012: 219−234. XIE Longhan, SHANG Tao. SPSS statistical analysis and data mining[M]. Beijing: Electronic Industry Press, 2012: 219−234.
(编辑 罗金花)
Model and its fast approximation algorithm of optimal route in a dual-weight emergency transportation network
GAI Wenmei1, 2, 3, DENG Yunfeng2, JIANG Zhongan1, LI Jing3, DU Yan1
(1. School of Civil and Environmental Engineering, University of Science and Technology Beijing, Beijing 100083, China;2. Chinese Academy of Governance, Beijing 100089, China;3. Institute of Public Safety, China Academy of Safety and Technology, Beijing 100012, China)
The graph theory and multi-objective optimization method were used to build a mathematical model for route selection in emergency network with double weights and a fast approximation algorithm was proposed to calculate it based on hyper-heuristic methodology. Several low-level heuristics were applied to get new heuristic algorithm and provide problem solving strategy for emergency decision-makers. Application effect of the designed algorithm in emergency management and decision-makingwas tested and compared with A* algorithm in a road map. A simulation was performed in different parameter settings of,,,1and2. The results show that the former has advantageson path optimization in an emergency network with double road-weights. The efficiency of the algorithm has a significant positive correlation with these parameters of,1and2, but not withand, and the proposed algorithm has a high efficiency which can provides powerful technical support for emergency decision and a strong powerful technical support for emergency relief and evacuation.
emergency management; path selection; dual-weight network; optimization model; hyper-heuristic algorithm
10.11817/j.issn.1672-7207.2015.06.050
X913.3;U116.2
A
1672−7207(2015)06−2366−10
2014−09−18;
2014−12−10
国家自然科学基金资助项目(71173198,91324017,71103162);国家科技支撑计划项目(2012BAK03B05,2012BAK20B02);中国安全生产科学研究院基本科研项目(2014JBKY02)(Projects (71173198, 91324017, 71103162) supported by the National Natural Science Foundation of China; Projects (2012BAK03B05, 2012BAK20B02) supported by the National Science & Technology Pillar Program; Project (2014JBKY02) supported by the Fundamental Scientific Project of China Academy of Safety Science and Technology)
蒋仲安,教授,博士生导师,从事矿山安全技术、矿井通风、职业危害与粉尘控制技术等研究;E-mail:jza1963@263.com

