环形单圈管冻结稳态温度场一般解析解
胡向东,韩延广
环形单圈管冻结稳态温度场一般解析解
胡向东1, 2,韩延广1, 2
(1. 同济大学岩土及地下工程教育部重点实验室,上海,200092;2. 同济大学地下建筑与工程系,上海,200092)
隧道联络通道和矿山竖井冻结法施工经常采用环形布置冻结管。对于环形布管冻结温度场的解,目前仅有冻结圈内完全冻实的单圈管冻结温度场解析解,但现实冻结工程中,内部通常是未冻实的。首先应用保角变换将环形单圈管冻结模型变换为易于求解的特殊的直线型排布的模型,再结合调和方程的边界条件可分离的性质,将问题分解为单排问题和线性温度场问题,最后完成单圈管冻结圈内未冻实的温度场解析解。热力学数值模拟计算对解析解的验证结果表明:在冻土帷幕充分交圈后,数值模拟结果和解析解结果基本一致,得到的解析解具有较高的精度。同时本文解析解也适用于冻结圈内完全冻实的温度场。
人工地层冻结法;环形单圈冻结管;温度场;解析解;保角变换;调和方程
人工地层冻结技术已发展成为一种成熟工法,在井矿工程、隧道工程、地基临时加固、地下水污染控制、废弃物掩埋等领域已有广泛应用。在施工过程中,掌握冻土帷幕的厚度和力学性质等参数是非常重要的,而这些参数均依赖于冻结温度场的分布。因此,温度场理论是冻结法理论的基础。目前冻结温度场的计算方法主要有解析法、模拟法以及数值分析方法。而解析解由于其理论性强,始终是研究温度场的重要部分。到目前为止,各国专家、学者们已经取得了一系列冻结管规则布置形式下的经典稳态温度场解析解。例如单管冻结温度场公式[1],两管~五管直线布置冻结温度场公式[2],单排管冻结温度场公式以及双排管冻结温度场公式[3−4]等,并且沿用至今。作者对这些公式进行了完善与应用性研究[5−9],并完成了三排管冻结温度场解析解的推导[10−15];对于环形布置冻结管的情形,完成了冻结圈内冻实的单圈管冻结温度场解析 解[16],对于内部未冻实的情况尚无解析解答。本文作者基于保角变换和调和方程边界条件可分离性[17],对环形单圈管冻结圈内未冻实的稳态温度场解析解进行了求解。
1 二维热传导方程
在土体中,热传递主要有3种形式:传导、对流和辐射。因为对流和辐射对温度场的影响相对于传导可以忽略不计,所以仅仅考虑传导形成的温度场[18]。
根据Fourier热传导定律和热量守恒律,可以得到二维热传导方程的形式[18]如下:
其中:为温度场的分布;为介质的热传导系数;为密度;为比热容;(,,)为单位时间单位体积系统吸收或者放出的热量。
人工地层冻结过程是一个瞬态热传导过程,是个具有相变并且相变界面移动的问题。对于采用稳态温度场近似瞬态温度场的适用性问题,学术界和工程界普遍接受的观点是:由于人工地层冻结是个发展相对缓慢的过程,尤其是在冻结的后期,其温度场非常接近稳态导热温度场,在人工地层冻结法的温度场理论与工程中,对此状态可按稳态导热近似求解人工冻结温度场。世界上最流行和实用的人工冻结温度场解析解有前苏联[1, 3]、美国[4]和日本公式[2],他们均为稳态温度场公式。对此问题,作者曾针对文献[3]的单排管和双排管冻结巴霍尔金公式的准确性进行了分析[20],结果表明,在冻结的中后期(/>0. 7,其中为冻土帷幕厚度,为冻结管间距),温度场任何一点的计算误差不超过1 ℃。因此在冻结的中后期,人工冻结温度场将可以近似当作稳态温度场。则;(,)=0,方程(1)简化为:
其极坐标下的表达式为:
2 单管的数学模型及解析解
单管在无限大地层形成的温度场的问题如图1所示。

图1 平面内单管的温度场问题
其数学模型如下:
通过分离变量法[17],求得满足上述调和方程的通解为:
(5)
将边界条件进行Fourier级数展开,仍为常数,即与无关,则a=0;b=0。
再将冻结管和冻土边界条件代入式(5)可以得到:
上式即为特鲁巴克单管冻结温度场。
3 单圈管冻结圈内未冻实的温度场
3.1 保角变换的应用
在冻土帷幕交圈后,冻土边界呈波浪形状。所以冻结圈内未冻实的环形单圈管冻结问题如图2所示。
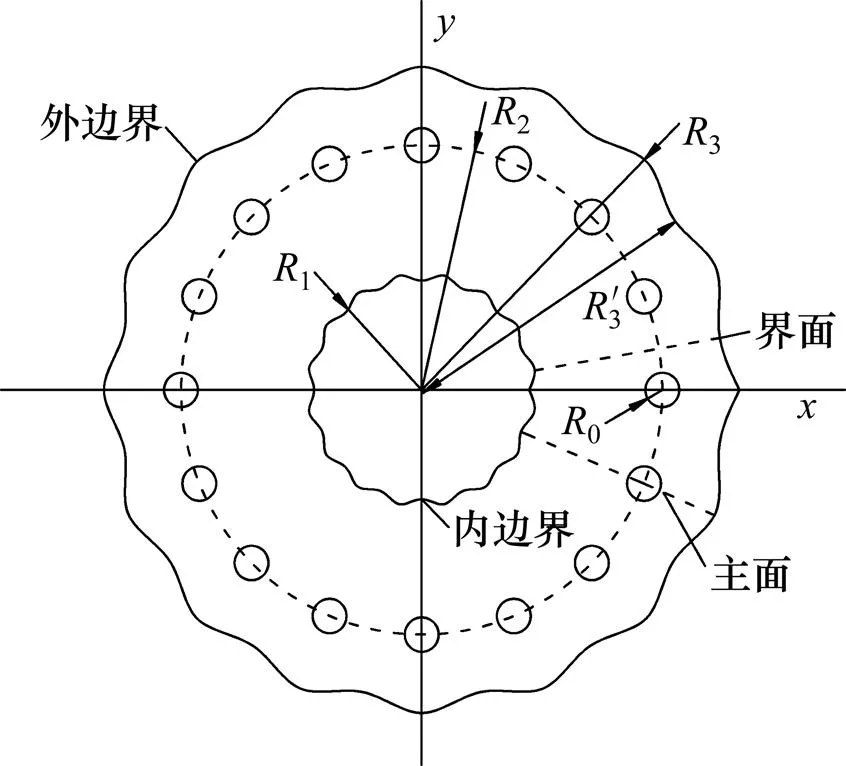
图2 单圈管冻结圈内未冻实的问题求解模型
其数学模型可以表达为
其中:为冻结管的数量,从0到−1取整数值。
由于直接求解上述问题较为困难,现引入保角变换,将其变换为较易解决的问题。变换函数为
其中平面为原平面(即物平面);平面为像平面。根据复变函数可以表示一个平面中的点,因此平面表示为=eiβ(其中为极径,为极角)。而将平面表示为=i(其中为平面中的横坐标,为其纵坐标)。将2个平面分别带入变换函数可以得到:
则物平面问题经过此种变换,其像平面问题如图3所示。

图3 像平面温度场问题
3.2 单排管冻结的巴霍尔金问题
单排管冻结时,在冻土帷幕交圈后,冻土帷幕边界为波浪形状,则其温度场问题如图4所示。
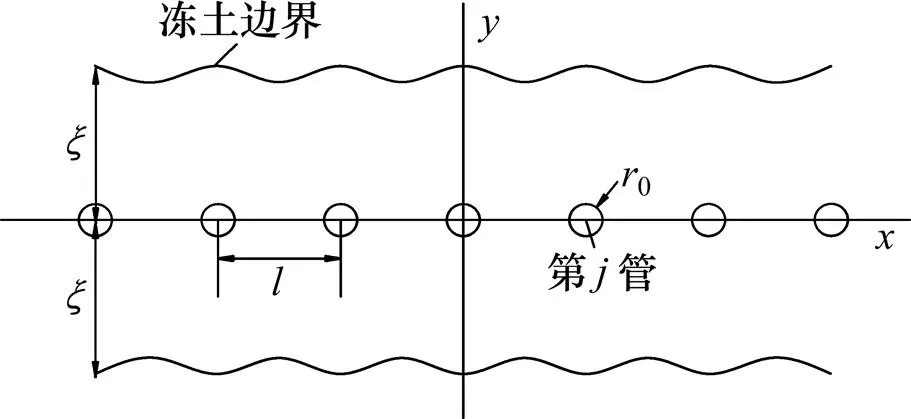
图4 平面内单排管的温度场问题
其数学模型为
利用调和方程的边界条件可分离性[17],将冻土边界条件和冻结管处条件均进行分解,将原问题分解为无限个单管冻结问题,则针对第管可以建立如下的数学模型:
根据冻土边界和冻结管条件的周期性,则θ;θ0为常数。即每根管温度场问题相同。
单排管冻结温度场解为无限个单管冻结温度场解的叠加:
根据贝塞特求和公式[21]:
整理式(13)得:
;
将冻土边界条件代入式(15),得:
再将冻结管处条件代入式(15),得:
因为ch2=2sh2+1,工程中<<1则;冻结中后期,则,,化简并求解式(16)和(17)得:

将其代入式(15),则
上式与巴霍尔金单排管冻结温度场的解析解[3]相同。
3.3 像平面温度场问题的解
对于图3表示的像平面温度场问题,其数学模型为:
根据边界条件可以分离性[17],上述问题可以分解为求解以下2个问题,然后再将解加起来即可得到原问题的解,即=1+2。
通过选取适当的θ可以保证式(20)为单排巴霍尔金问题。由冻土内边界和冻结管条件,根据单排巴霍尔金解(18),其解可以表达为:
则将冻土外边界条件代入式(22)得到:
而对于式(21),由于冻结管半径很小,在不引起大的误差的前提下,为了便于计算,将冻结管处条件简化为。选取适当的T可以保证其解为线性温度场。则
将冻结管处条件代入(24)得到
联立式(23)和(25)可以解出
将式(26)代入式(22)得:
将式(27)代入式(24)得:
3.4 物平面温度场的解析解
3.5 冻土帷幕形状特征
理论上讲,冻土帷幕边界应随冻结管位置呈波浪形,现考察其特征。按命题,冻土边界各处温度相等,故外边界主面(=0°的面)与外边界界面(=±180°/的面)位置处的温度之差D=0(见图2)。由式(31),得
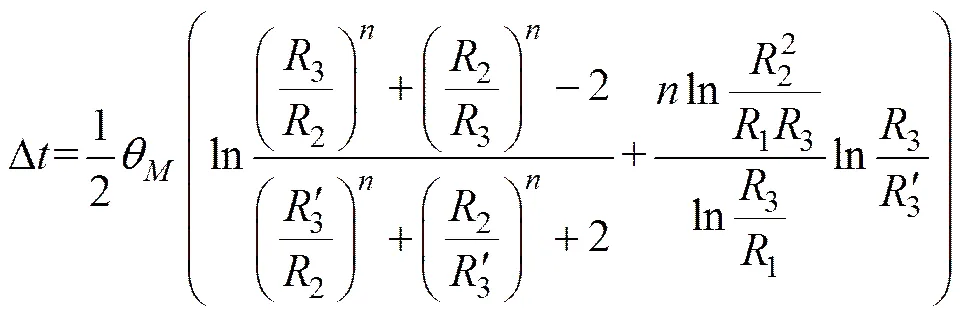
从上述判定过程可以看出,在满足冻结中后期(帷幕厚度较大)和冻结管数较多(工程常用布孔参数)的情况下,即满足化简过程的参数条件时,主面厚度和界面厚度基本一致,则冻土边界形状可以当作环形,其波浪形可以忽略。这一结论不适用于不能构成环形布孔的过少冻结管的情况。
3.6 解析解准确性检验
解析解推导过程中采用了一定的简化处理,故有必要对解的准确性进行验证。因为数值模拟能够较好的反应人工冻结温度场的分布,所以用ANSYS热力学数值模拟来检验解析解的结果。根据一般的工程实际,选取参数。环半径2一般在2.5~8.0 m;管间距一般取值为0.5~1.2 m;帷幕厚度与管间距比值一般为0.5~1.5;而且内侧冻土帷幕与外侧冻土帷幕比值1/2一般介于1和0.55:0.45之间。冻结管半径0.054 m;冻结管表面温度θ=−30 ℃;冻土边界温度0=0 ℃。本次数值模拟共分4组。每组的参数列于表1。

表1 单圈管冻结数值模拟参数
上述模拟参数属工程常用参数范围内,满足3.5节的参数要求,故采用环形边界进行数值模拟。又由于问题的周期性,采取包含一个冻结管的圆心角为360°/的扇形进行模拟。其中主面为=0°的面;界面为=±180°/的面。第1组模拟的网格划分图和温度场云图如图5和6所示。各组模拟对比结果如图7 所示。
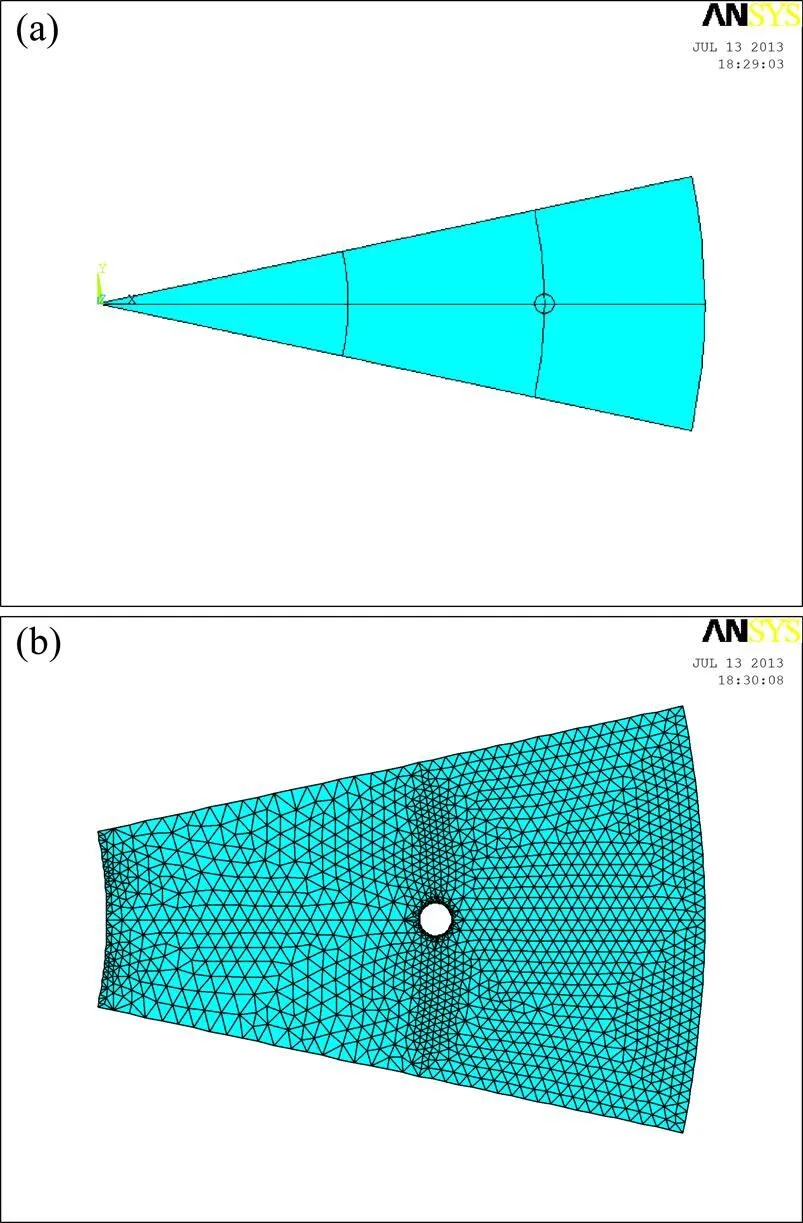
图5 第1组数值模拟模型及网格划分
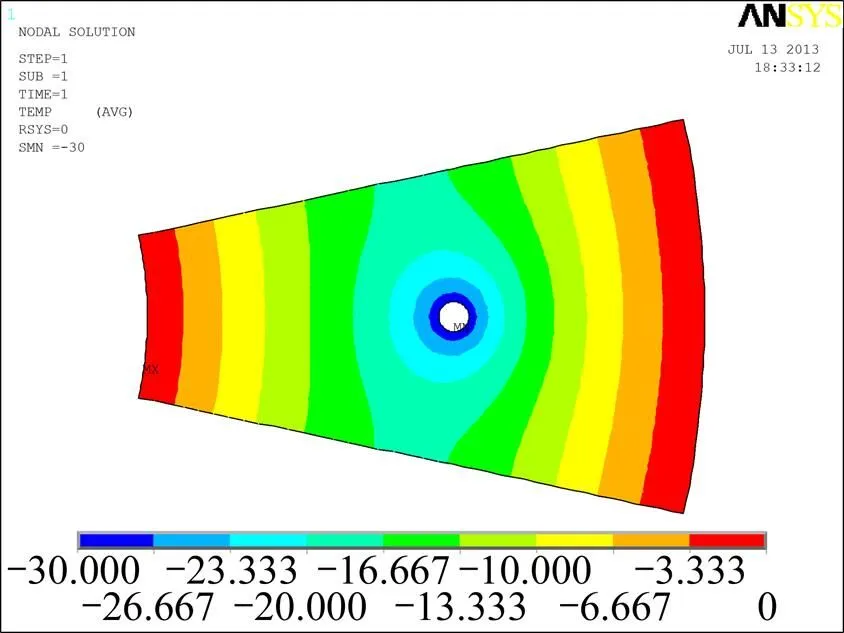
图6 第1组数值模拟结果温度云图
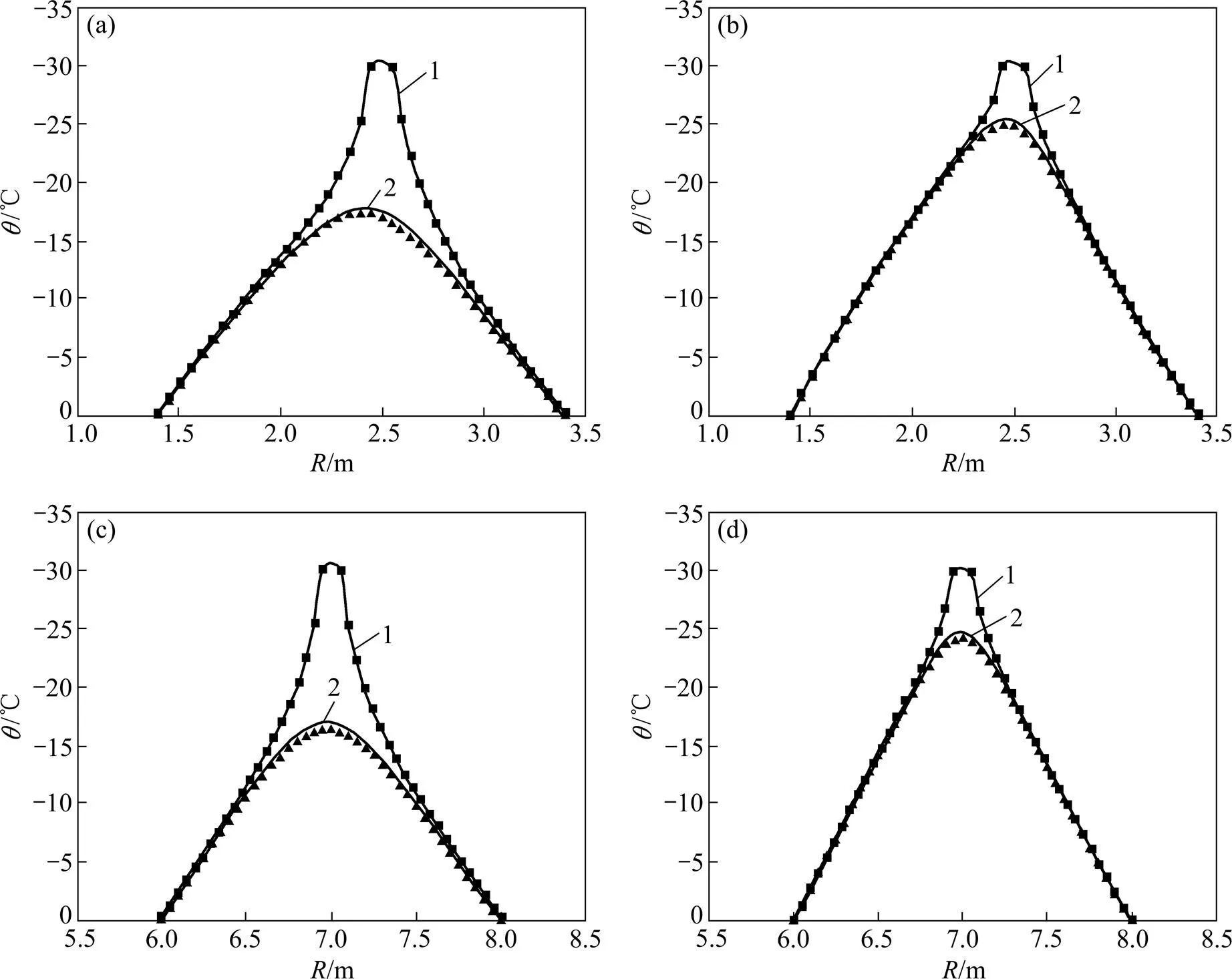
(a) 组1;(b) 组2;(c) 组3;(d) 组4
通过上述对比结果可以知道,数值解和解析解基本一致。说明在工程中常用的参数范围内,本文求得的单圈冻结圈内未冻实的温度场的解析解具有较高的准确性。不仅说明了采用圆弧面边界模型进行数值模拟是可行的,同时也说明了在工程常用布孔参数范围内并在冻结的中后期,波浪形边界可以看作环形边界的结论的正确性。
3.7 与冻结圈内冻实的温度场解析解对比
对于式(31),若考虑1趋向于0,即极限时,冻结圈内处于完全冻实状态,则
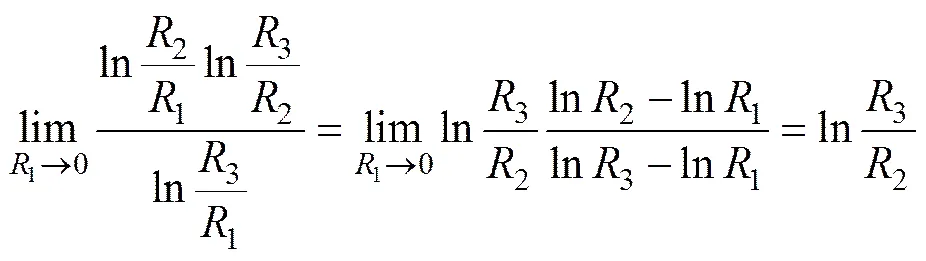
此时式(31)简化为:
已有的冻结圈内部完全冻实的温度场解析解[16]为:
当的取值范围在冻土帷幕以内时,即<3,则,>>。
所以,在这种情况下,式(34)将可以近似代替式(35),出现的误差可以忽略。
因此本文求得的温度场解析式既适合于冻结圈内未冻实的情况,也适合于冻结圈内完全冻实的情况。
4 结论
1) 应用调和方程的边界条件可分离性,将经典的单排巴霍尔金问题分解为无数个单管冻结问题,以此重现了巴霍尔金解。
2) 通过保角变换将冻结圈内未冻实的单圈管冻结问题转化为特殊的单排冻结问题,再次以调和方程边界条件可分离性,将问题分解为已有解的单排巴霍尔金问题和线性温度场的问题,完成了单圈管冻结内部未冻实的温度场解析式。并且此公式也可以针对冻结圈内部完全冻实的情况。
3) 在工程合理参数范围下,冻结中后期,冻土帷幕边界之波浪形极不明显,可视作环形。
[1] Trupak N G. Ground freezing in shaft sinking[M]. Moscow: Coal Technology Press, 1954: 20−65.
[2] Tobe N, Akimoto O. Temperature distribution formula in frozen soil and its application[J]. Refrigeration, 1979, 54: 3−11.
[3] Bakholdin B V. Selection of optimized mode of ground freezing for construction purpose[M]. Moscow: State Construction Press, 1963: 21−27.
[4] Sanger F J. Ground freezing in construction[J]. Journal of the Soil Mechanics and Foundations Division, Proceedings of ASCE, 1968, 94(SM1): 131−158.
[5] HU Xiangdong. Average temperature model of double-row-pipe frozen soil wall by equivalent trapezoid method[C]//AIP Conference Proceedings. New York: American Institute of Physics, 2010: 1333−1338.
[6] 胡向东, 黄峰, 白楠. 考虑土层冻结温度时人工冻结温度场模型[J]. 中国矿业大学学报(自然科学版), 2008, 37(4): 550−555. HU Xiangdong, HUANG Feng, BAI Nan. Models of artificial frozen temperature field considering soil freezing point[J]. Journal of China University of Mining & Technology (Natural Science), 2008, 37(4): 550−555.
[7] 胡向东, 白楠, 余锋. 单排管冻结温度场Тrupak和Bakholdin公式的适用性[J]. 同济大学学报(自然科学版), 2008, 36(7): 906−910. HU Xiangdong, BAI Nan, YU Feng. Analysis of Trupak and Bakholdin formulas for temperature field of single-row-pipe frozen soil wall[J]. Journal of Tongji University (Natural Science), 2008, 36(7): 906−910.
[8] 胡向东. 直线形单排管冻土帷幕平均温度计算方法[J]. 冰川冻土, 2010, 32(4): 778−785. HU Xiangdong. Average temperature calculation for the straight single-row-pipe frozen soil wall[J]. Journal of Glaciology and Geocryology, 2010, 32(4): 778−785.
[9] 胡向东, 赵飞, 佘思源, 等. 直线双排管冻结壁平均温度的等效抛物弓形模型[J]. 煤炭学报, 2012, 37(1): 28−32. HU Xiangdong, ZHAO Fei, SHE Siyuan, et al. Equivalent parabolic arch method of average temperature calculation for straight double-row-pipe frozen soil wall[J]. Journal of China Coal Society, 2012, 37(1): 28−32.
[10] HU Xiangdong, ZHANG Luoyu. Analytical solution to steady-state temperature field of one and two freezing pipes near linear adiabatic boundary[C]//ICDMA 2013. Qindao, 2013: 257-260.
[11] HU Xiangdong, ZHANG Luoyu. Analytical solution to steady-state temperature field of two freezing pipes with different temperatures[J]. Journal of Shanghai Jiaotong University (Science), 2013, 18(6): 706-711.
[12] 胡向东, 郭旺, 张洛瑜. 无限大区域内少量冻结管稳态温度场解析解[J]. 煤炭学报, 2013, 38(11): 1953-1960.
Hu Xiangdong, Guo Wang, Zhang Luoyu. Analytical solution of steady state temperature field of a few freezing pipes in infinite region[J]. Journal of China Coal Society, 2013, 38(11):1953-1960.
[13] 胡向东, 郭旺, 张洛瑜. 无限大区域内四管冻结的稳态温度场解析解[J]. 上海交通大学学报, 2012, 47(9): 1367-1371.
HU Xiangdong, GUO Wang, ZHANG Luoyu. Analytical solution of steady state temperature field of four freezing pipes in an infinite region[J]. Journal of Shanghai Jiaotong University, 2012, 47(9): 1367-1371.
[14] 胡向东, 汪洋. 三排管冻结温度场的势函数叠加法解析解[J]. 岩石力学与工程学报, 2012, 31(5): 1071−1080. HU Xiangdong, WANG Yang. Analytical solution of three-row-piped frozen temperature field by means of superposition of potential[J]. Chinese Journal of Rock Mechanics and Engineering, 2012, 31(5): 1071−1080.
[15] 胡向东, 任辉. 3 排管冻结梯形-抛物弓叠合等效温度场模型和平均温度[J].煤炭学报, 2014, 39(1):78-83.
HU Xiangdong, REN Hui. A trapezoidal-parabolic arch superimposed equivalent temperature field model and its average temperature formula for triple-row-pipe freezing[J]. Journal of China Coal Society, 2014, 39(1): 78-83.
[16] 胡向东, 陈锦, 汪洋, 等.环形单圈管冻结稳态温度场解析解[J]. 岩土力学,2013, 34(3):874−880. HU Xiangdong, CHEN Jin, WANG Yang, et al. Analytical solution to steady-state temperature field of single-circle-pipe freezing[J]. Chinese Journal of Rock and Soil Mechanics, 2013, 34(3): 874−880.
[17] 陈恕行, 秦铁虎, 周忆. 数学物理方程[M]. 上海: 复旦大学出版社, 2003: 35.CHEN Shuxing, QIN Tiehu, ZHOU Yi. Mathematical physics equation[M]. Shanghai: Fudan University Press, 2003: 35.
[18] Carslaw H S, Jaeger J C. The conduction of heat in solids[M]. London: Oxford University Press, 1959: 1.
[19] Jiji L M. Heat conduction[M]. Berlin: Springer Berlin Heidelberg, 2009: 2−9.
[20] 胡向东, 赵俊杰. 人工冻结温度场巴霍尔金模型准确性研究[J]. 地下空间与工程学报, 2010, 6(1): 96−101. HU Xiangdong, ZHAO Junjie. Research on precision of Bakholdin model for temperature field of artificial ground freezing[J]. Chinese Journal of Underground Space and Engineering, 2010, 6(1): 96−101.
[21] Hurst W. Reservoir engineering and conformal mapping of oil and gas field[M]. Tulsa. Oklahoma: The Petroleum Publishing Company, 1979: 115−118.
(编辑 陈爱华)
General analytical solution to steady-state temperature field of single-circle-pipe freezing
HU Xiangdong1, 2, HAN Yanguang1, 2
(1. Key Laboratory of Geotechnical and Underground Engineering of the Ministry of Education,Tongji University,Shanghai 200092, China;2. Department of Geotechnical Engineering, Tongji University, Shanghai 200092, China)
Single-circle-pipe freezing method is often applied in cross passage construction and mine shaft sinking. At present, there is only one analytical solution which is aimed at the situation that the ground inside the freezing-pipe circle is frozen solid. However, a more usual situation is that the area enclosed inside the freezing-pipe circle is not frozen completely. For this situation, an analytical solution to the steady-state temperature field of single-circle-pipe freezing was proposed. The solution was derived by converting the single-circle-pipe freezing model to a special single-row-pipe freezing model using conformal mapping, and then decomposing the single-row-pipe freezing model into the single-row-pipe freezing model and a linear temperature field model according to the separability of boundary conditions for harmonic equations. Comparison of the analytical solution with the numerical thermal analysis shows that the analytical solution is precise enough. Furthermore, the solution can also be employed for the temperature field of the frozen-solid situation.
artificial ground freezing; single-circle-pipe freezing; temperature field; analytical solution; conformal mapping; harmonic equations
10.11817/j.issn.1672-7207.2015.06.047
TK124
A
1672−7207(2015)06−2342−08
2014−04−13;
2014−08−20
国家自然科学基金资助项目(51178336,51478340);浙江省自然科学基金资助项目(LZ13E080002)(Project (51178336, 51478340) supported by the National Natural Science Foundation of China; Project (LZ13E080002) supported by the Natural Science Foundation of Zhejiang Province, China)
胡向东,副教授,博士生导师,从事隧道及地下工程研究;E-mail:anton.geotech@tongji.edu.cn

