基于多区域划分的模糊支持向量机方法
查翔,倪世宏,张鹏
基于多区域划分的模糊支持向量机方法
查翔,倪世宏,张鹏
(空军工程大学航空航天工程学院,陕西西安,710038)
针对模糊支持向量机(FSVM)方法无法有效定位支持向量,在确定隶属度时易丢失分类信息的问题,提出一种基于多区域划分的FSVM方法。该方法先利用传统SVM获取支持向量的大体位置,作为对FSVM支持向量的近似估计,再进一步融合带负类样本的支持向量域描述(SVDD-neg)模型,对样本空间进行划分,最后根据样本所在的区域按不同的规律确定隶属度。研究结果表明:这种隶属度确定方式不仅能有效削弱野值样本的影响,而且也会提高支持向量的隶属度。与基于样本紧密度以及基于样本到类内超平面距离的FSVM方法相比,该方法具有更好的抗噪性能和泛化能力。
模糊支持向量机;多区域划分;野值;支持向量;隶属度
支持向量机(support vector machine,SVM)[1]是在统计学习理论和结构风险最小化基础上发展起来的一种新的机器学习方法,特别是在解决小样本、局部极小、高维和非线性模式识别中表现出较强的泛化能力。但SVM在构建最优分类面时视所有样本为等价的,当样本中存在野值或孤立点时,容易造成过学习的现象。为此,Lin等[2]引入模糊理论中的隶属度概念,提出了模糊支持向量机(fuzzy support vector machine,FSVM)方法,按照不同样本有不同贡献的原则,为野值样本分配较低的隶属度,以降低其对分类面决策的影响。FSVM中的隶属度要求能够客观反映样本的不确定性,因此如何合理地选择隶属度函数是算法的关键[3−6]。目前,隶属度函数的确定主要包括基于样本到类质心距离的方法[7−13]以及基于类质心几何划分的方 法[14−15]。基于样本到类质心距离的方法主要以样本到类中心间的距离作为确定隶属度的依据,距离越大,样本的隶属度越低。由于支持向量在空间上可能与野值相邻,导致野值在被赋予较低隶属度的同时支持向量的隶属度也较低,因此这些方法在降低野值作用的同时也削弱了支持向量对分类的影响,一定程度上影响了最优超平面的确定。基于类质心几何划分的方法利用各类样本的质心作不同的辅助模型,从而实现对样本空间的划分,能够提高支持向量的隶属度,然而它们都是通过几何空间的划分估计支持向量的大致位置,因此会受到类质心位置的过度约束,使分类面朝着类中心连线的垂直方向发生倾斜,结果未必是真正最优的。针对上述问题,本文作者根据支持向量与野值的分布特点,提出了一种基于多区域划分的模糊支持向量机(fuzzy support vector machine based on multi- region partition,FSVM-MP)。该方法保证了在降低野值和非支持向量隶属度的同时,能够弥补几何划分的缺陷,提高支持向量的隶属度。
1 模糊支持向量机方法
由于FSVM比传统SVM的样本要多出一项隶属度,因此需要对训练集重新定义。设样本集={ (1,1,(1)), (2,2,(2)),…, (x,y,(x)) },x∈R,y∈{−1, +1},= 1, 2, …,,(x)为隶属度函数,且(x) ∈(0, 1],代表样本x属于y类的可靠程度。FSVM的本质也是求解最优分类超平面,具体可归结为求解以下二次规划问题:
其中:和分别为超平面的法向量和偏置项;为惩罚因子;ξ为松弛变量。
对于固定的,不同的(x)会对FSVM的训练施加不同的影响,(x)越大,这种影响就越显著。传统SVM对每个样本等价对待,隶属度均为1。在FSVM中,若为野值样本分配较低的隶属度,则其对FSVM产生的影响就会大大减少;若其他有效样本的隶属度很高,则它们所起的作用与在SVM中的一样。因此,需要根据样本的重要性程度选取合适的隶属度函数,它是否合理将直接影响到FSVM的分类性能。
2 基于多区域划分的隶属度确定方法
对样本附加隶属度并运用到FSVM的训练中,是提高FSVM抗噪性能的重要环节。虽然野值可通过某种途径进行隔离[16],但由于支持向量的位置信息无法事先获取,也就很难为支持向量分配较高的隶属度。本文首先通过建立预置超平面模型来估计支持向量的大体位置,并构造超球模型对野值进行隔离;然后以这2个模型为基础,将样本空间划分成多个区域,根据样本所在的区域为样本分配对应的隶属度,力求在削弱野值影响的同时能够增强支持向量的作用。
2.1 支持向量信息的获取
SVM和FSVM建模的思想都是通过最优分类面实现对样本的分类和识别,而支持向量通常分布在最优分类面附近。考虑到SVM本身具有较高的分类性能,可将SVM分类面作为对FSVM最优分类面的近似,或者作为FSVM预置的参考超平面。在没有任何支持向量先验知识的情况下,采用预置超平面的方法可较好地识别出样本的类别结构,获得FSVM支持向量大致的位置信息,便于为其分配较高的隶属度。同时,野值常混杂在其他类样本中,SVM很容易将其判断为错分点,这样在设置隶属度时可被分配更低的值。
建立SVM模型以获取预置超平面的过程可参考文献[1]。在特征空间中得到的最优判别函数为,用来检验预置超平面对的判别结果。若()=+1,说明预置超平面对正确分类,若()=−1则错误分类。
2.2 野值样本的隔离
超球模型可较好地描述样本的分布,衡量样本的离散情况,也为野值的判断提供了手段。本文作者采用带负类样本的支持向量域描述(support vector domain description with negative examples,SVDD-neg)[17−18]方法,以寻找包含大多数样本的最小超球。这里统一将当前研究的目标类样本称为正类,其他类样本称为负类。SVDD-neg在确定最小化的球半径时将负类样本信息考虑在内,这能极大地改善正类样本不完备时的数据描述,获得更紧致的样本边界。目标类样本的野值常分布于其他类样本中,由SVDD-neg得到的超球模型不仅能将野值与有效样本进行隔离,而且还会充分利用负类样本的信息,增加对野值的排斥程度。
设正、负类的样本数分别为1和2,=1+2,在特征空间中,求解正类样本的SVDD-neg超球模型可归结为以下二次规划问题:
其中:1为正类超球的最小半径;1为球心;ξ和ξ为松弛变量;(·)代表从原始样本空间到特征空间的某非线性映射。对上述问题求解,便可得到超球的球心1和半径1:
2.3 隶属度函数的确定
在特征空间中,考虑更一般的预置超平面与正类超球相交的情形,如图1所示。

图1 正类样本的区域划分
在图1中,“○”和“+”分别代表正、负类样本;1为正类超球的球心,1为半径;为预置超平面。从图1可见:正类样本空间被预置超平面和超球模型划分成了4个不同的区域1~4:1和2组成了关于预置超平面正确分类一侧的区域,3和4组成了关于预置超平面错误分类一侧的区域;1和3位于超球内,而2和4位于超球外。另外在图1中标识出了2个距离变量H()和S(),其中H()为任意正类样本到预置超平面的特征距离(量纲一),反映了样本偏离预置超平面的程度;S()为任意正类样本与正类球心1之间的特征距离(量纲一),反映了样本偏离正类总体的程度,可根据S()≤1判断其是否位于超球内。各变量的计算方法为:
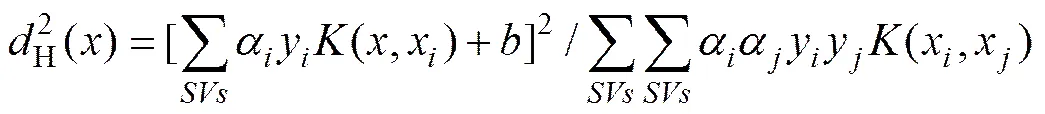
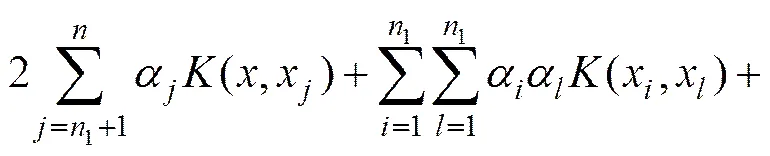
(8)
在确定隶属度函数时应满足如下原则:
1) 考虑到野值对分类的影响,样本的隶属度应随S的增加而逐步降低,并且野值应被隔离在超球外,与其他有效样本分开。
2) 支持向量通常分布在分类面附近,而包括野值在内的其他非支持向量样本距分类面较远。根据这一特点,若某个样本的H越小,越有可能成为支持向量,为其分配的隶属度也应越高,而野值的d通常较大,对应的隶属度也应较低,因此隶属度函数应与H的变化趋势相反。
3) 位于预置超平面错误分类一侧中的样本,相对于正确分类的一侧来说,其为野值的可能性更高,在隶属度函数设计中应能凸显这种差异。
对于以上原则,本文采取如下方案:
1) 以超球半径1为界,可在超球内外按不同的方式定义隶属度。超球外样本的隶属度随S的增加,下降幅度应进一步变快,使野值获得更低的隶属度。
2) 针对支持向量和野值相对于分类面的分布特点,可利用以H作为自变量的指数函数来衡量样本对分类的作用,具体表现为在H较小时隶属度较高,随着H的增加隶属度会急剧下降。
3) 在预置超平面两侧可利用不同的控制参数,使超平面两侧的隶属度函数有不同的变化规律。
由实现方案可知,基于多区域划分的隶属度函数主要包含了2个部分:受所处超球位置影响的隶属度以及受预置超平面影响的隶属度,具体的隶属度函数()计算公式为(按1~4的顺序):

其中:自变量为任意正类样本;1和2为控制参数,且有2>1>0,目的是保证位于预置超平面两侧的样本,其隶属度有不同的下降速率。由式(9)可知:决策函数()的取值与控制参数的选取是一一对应的,也就是说,()=+1对应区域1和2,此时控制参数为1;()=−1对应区域3和4,此时控制参数为2。
1和2除满足上述条件外,还应保证在合理范围内取值,防止预置超平面和超球两个模型各自占优。为合理选取控制参数,给出在二维正类样本空间中,当1和2取不同值时()的分布情况,如图2所示。

(a) p1=0.1, p2=0.2; (b) p1=1, p2=2; (c) p1=7, p2=8
从图2可以看出:在满足2>1>0的前提下,()是否合理主要由参数值的数量级决定。当控制参数取较小值时(见图2(a)),()在样本空间中呈现类球形分布,不能很好地突出预置超平面的作用,以致降低了支持向量对分类的影响;当控制参数取较大值时(见图2(c)),()中指数部分占绝对优势,导致()在预置超平面两侧的下降速度很快,受超球模型的影响不明显,无法充分削弱野值的作用;当控制参数取某些中间值时(见图2(b)),靠近球心且离超平面较近的样本,隶属度会取得较大值,而位于超球外且错分的样本随着H和S的同时增大,隶属度会迅速减小,此时隶属度的分布比较理想。为使2个模型对()的影响相当,通过对比多组不同控制参数下()的分布情况,可将参数的取值范围设定为[1,5],本文取1=1,2=2。
2.4 对隶属度函数的分析
由()的定义,样本隶属度的影响因素包括所处超球的位置以及预置超平面。由式(9)可知:这一部分的隶属度与决策函数()的取值无关。图3所示为()=+1样本H不同时的隶属度随S的变化情况(假设1=1)。
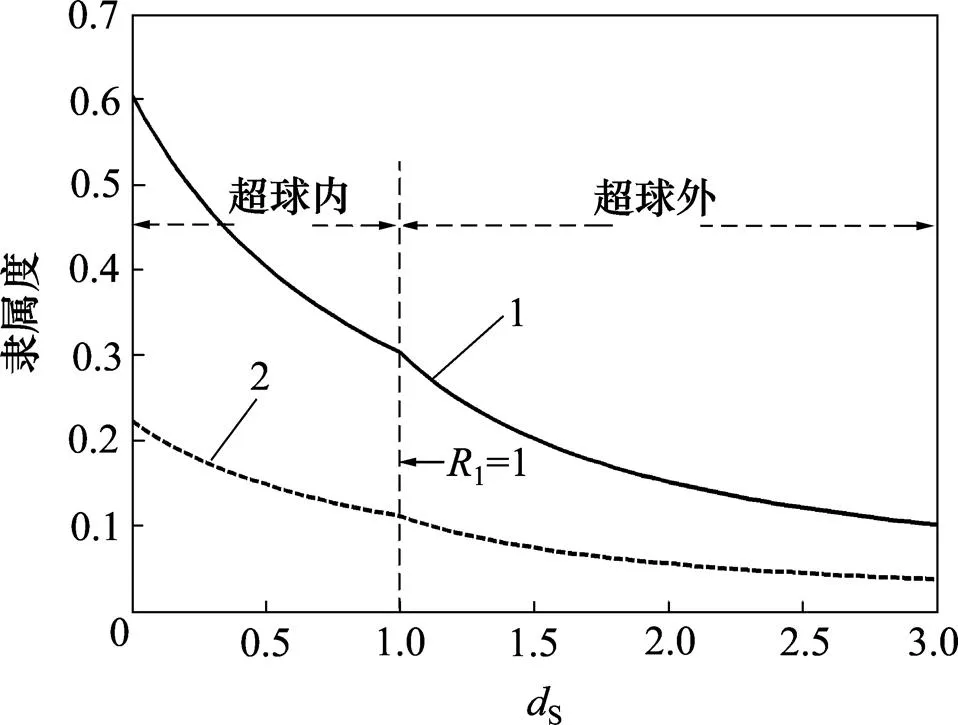
dH: 1—0.5; 2—1.5
由图3可以看出:若固定样本到超平面的距离H,此时隶属度主要受样本所处超球位置的影响,随着样本到球心距离的增加,隶属度整体呈下降趋势。考虑到样本集在超球内外有不同的分布密度,位于超球外的样本下降幅度更快。
若样本到球心的距离S相同,则意味着它们分布在同心球面上,此时隶属度主要受预置超平面的影响。图4所示为不同()和S下样本的隶属度随H的变化情况(假设1=1)。

1—f(x)=1, dS=0.5; 2—f(x)=1, dS=1.5; 3—f(x)=−1, dS=0.5; 4—f(x)=−1, dS=1.5
从图4可以看出:在任一情形下,随着H的增加,样本的隶属度均以指数规律迅速降低,使分布在预置超平面附近的支持向量获得很高的隶属度,而距预置超平面较远的野值获得很低的隶属度。当()相同时,样本到球心的距离S越大,隶属度整体越低,若样本被划分在超球之外,只要其距超平面足够近,就有可能是潜在的支持向量,其隶属度仍然能够获得较高的值,从而尽可能保留样本的分类信息。
()对隶属度函数的影响主要体现在控制参数1和2上。当()不同时,样本位于预置超平面的不同侧区域,并且由于不同侧区域的控制参数也不相同,位于错误分类区域的样本的隶属度的下降速率要比正确分类区域的样本的大。对于S和H均相同的位于不同侧区域的2个样本,被判别为错误的样本为野值的可能性更大,对应的隶属度也较低,因此利用控制参数可进一步降低野值的隶属度。
3 仿真实验
3.1 人工数据集实验
FSVM-MP对隶属度的分配情况如图5所示,其中,H1和H2分别代表正类和负类超球边界;H3代表预置超平面。在原始样本空间中共选取了9个样本,并在各样本下方对序号进行了标注,其中样本28和102明显属于野值样本。按FSVM-MP计算出9个样本的隶属度,结果见表1。
由图5和表1可知:对于野值样本28和102,与传统FSVM一样,FSVM-MP为它们分配的隶属度也是同类样本中相对较低的。在所有选取的样本中,样本7,43和52属于隶属度较高的3个样本,并且均分布在2类样本的临近区域,成为支持向量的概率很大,从而被分配了较高的隶属度。因此,采用基于多区域划分的隶属度分配方式,既能充分降低野值对分类的影响,又能最大限度地利用样本的分类信息。
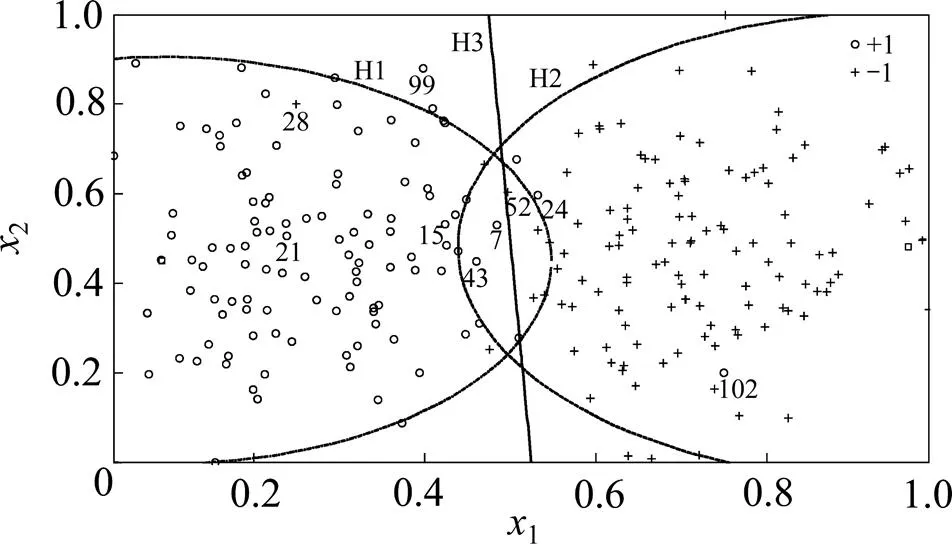
图5 超球和预置超平面下样本的划分结果
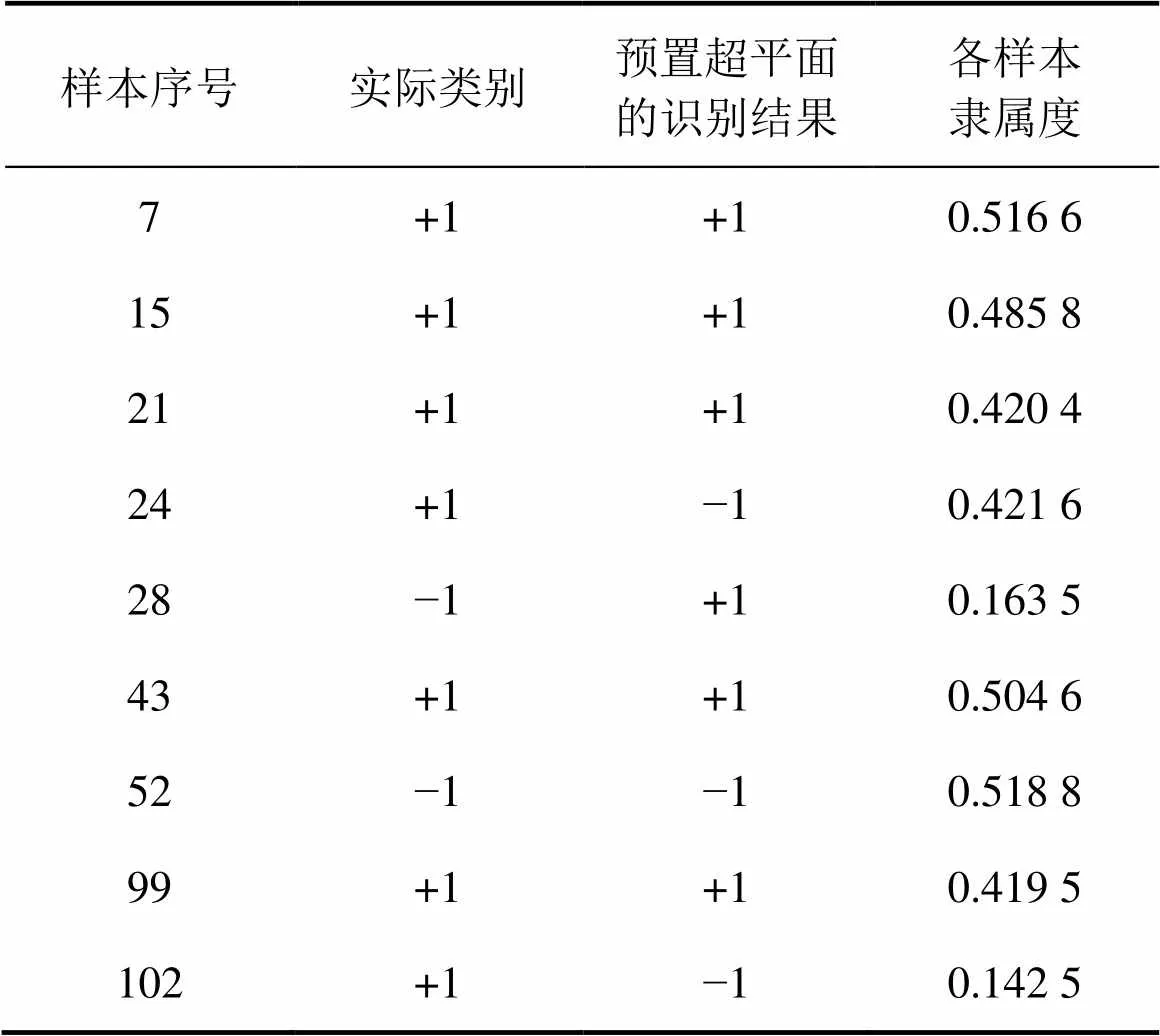
表1 典型样本的实验结果
考虑到该方法在原始二维样本空间中的分类结果主要由一条分类直线体现,无法较好地说明对野值的隔离作用,可利用高斯径向基(GRBF)核函数将样本映射到特征空间中。图6所示为FSVM-MP与传统SVM的分类结果。利用网格搜索与交叉验证相结合的方 法[19]得到GRBF核函数的最优参数,如表2所示。
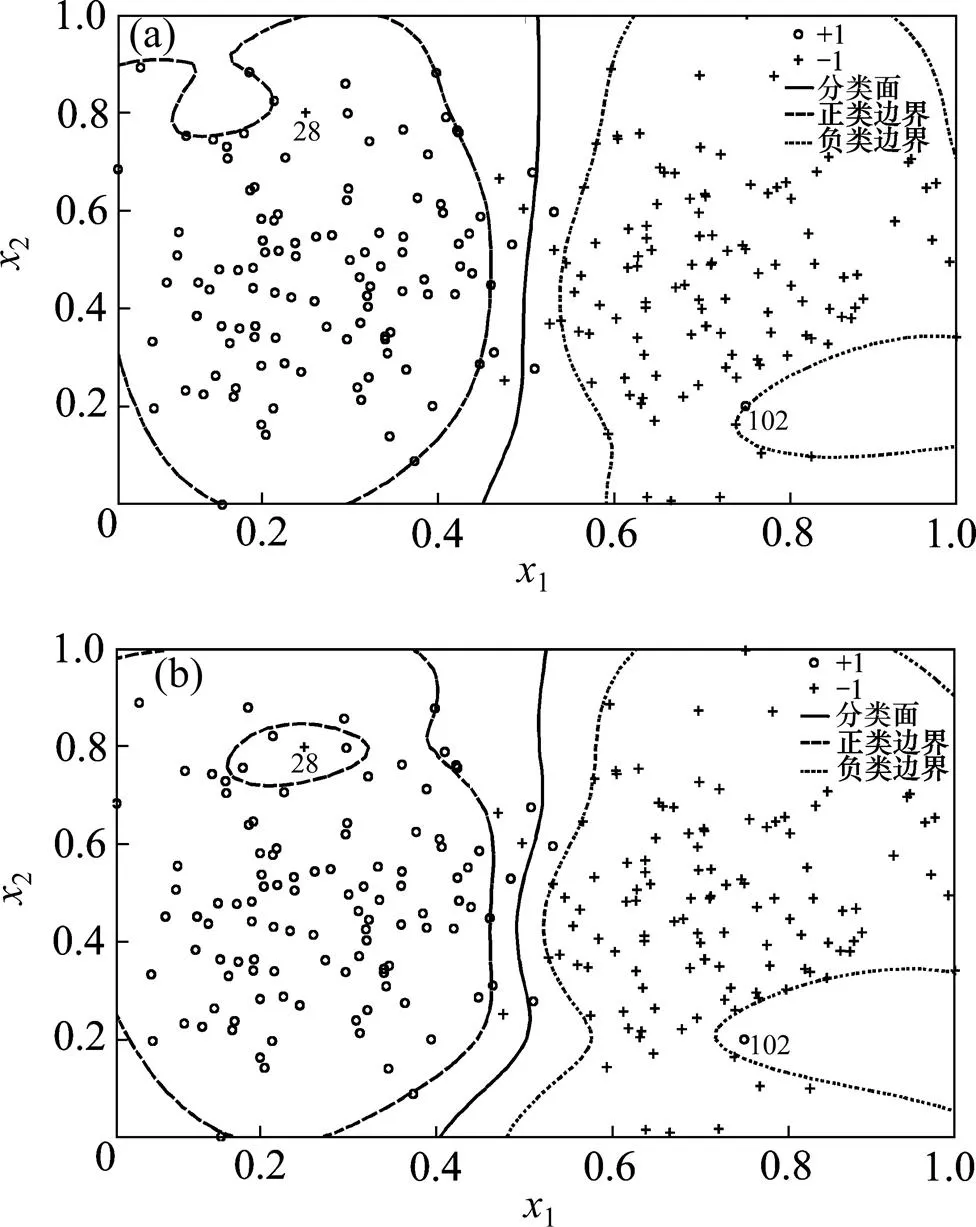
(a) FSVM-MP;(b) SVM
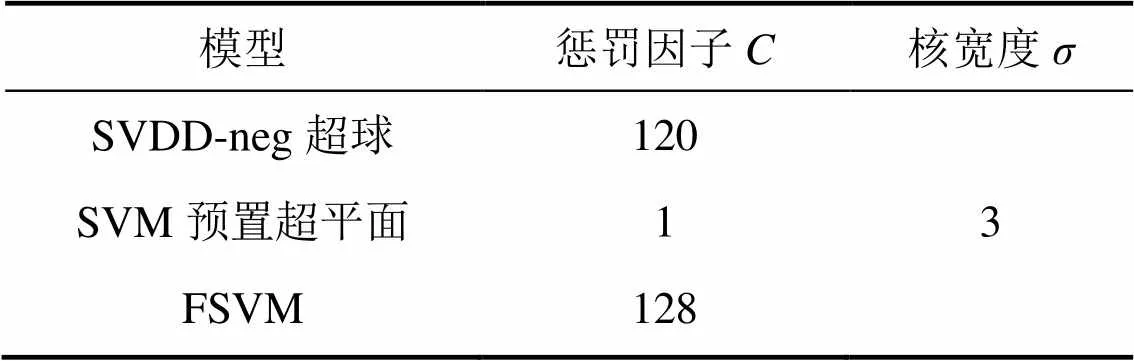
表2 人工数据集上各模型的参数设置
由图6可以看出:由于野值样本28和102的存在,2种方法得到的分类面完全不同。传统SVM将所有样本等价对待,未能隔离出野值;而FSVM-MP通过为野值分配较低的隶属度,将各野值隔离出对应类样本之外,从而能够降低其对分类的影响。
为检验FSVM-MP方法的优越性,这里将其与基于紧密度(FSVM-AAS)[8]和基于类内超平面 (FSVM-HC)[14]的方法进行比较。具体做法是:根据各方法对上述二维人工数据集分别进行训练,然后利用randn函数产生3组不同数目的样本,并在每一组样本下对各方法进行分类测试。各分类器的性能用误分率来衡量,采用GRBF核函数,参数设置与表2相同。共进行20次实验,得到各方法的平均实验结果如表3所示。

表3 3种方法在人工数据集上的分类结果
由表3可知:在不同的样本集规模下,各方法的平均误分率整体较低,均保持在9%以内,适用性较好。但本文提出的FSVM-MP与其他2种模糊方法相比,取得了相对较低的误分率,分类性能较好。这是由于FSVM-AAS仅考虑了野值的作用;FSVM-HC虽然能够提高支持向量的隶属度,但对支持向量的位置信息无法有效地获取; FSVM-MP不仅考虑了野值的影响,还通过预置超平面近似估计出支持向量的位置,尽可能利用了样本的分类信息。
3.2 UCI数据集实验
这里选取UCI机器学习库[20]中的真实样本集进行实验,并将FSVM-MP方法与FSVM-AAS,FSVM-HC方法进行分类性能的比较。由于多类别样本可转化为一系列二分类问题,因此本实验仅选取了5个二分类样本集。所选各数据集的特征描述如表4所示,其中样本数为去掉丢失值后的总实例数。由表4可以看到:5个数据集的样本数以及特征数均不相同。为减少不同量纲对分类性能的影响,实验前对每个样本集均进行了归一化处理,仍然采用GRBF核函数。在这5个样本集上同样进行20次实验,得到各方法平均误分率如表5所示。
覆盖林区的通讯设备设施不健全,一些林区道路建设不到位,森林火灾隐患增强。扑火装备机械化程度不高及扑灭森林大火能力不强,在发生紧急情况时,很难及时扑救,损失严重。生物防火林带和防火隔离带的建设滞后,原有防火林带和生土带年久失修、杂草丛生,失去防火功能,有的甚至变成引火载体。
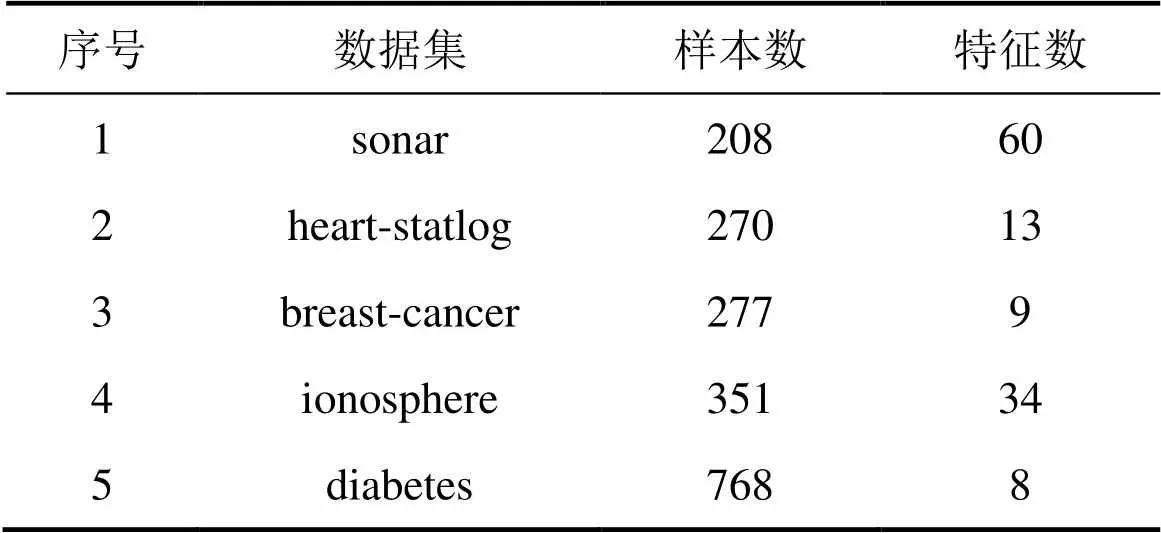
表4 UCI数据集的数据特征
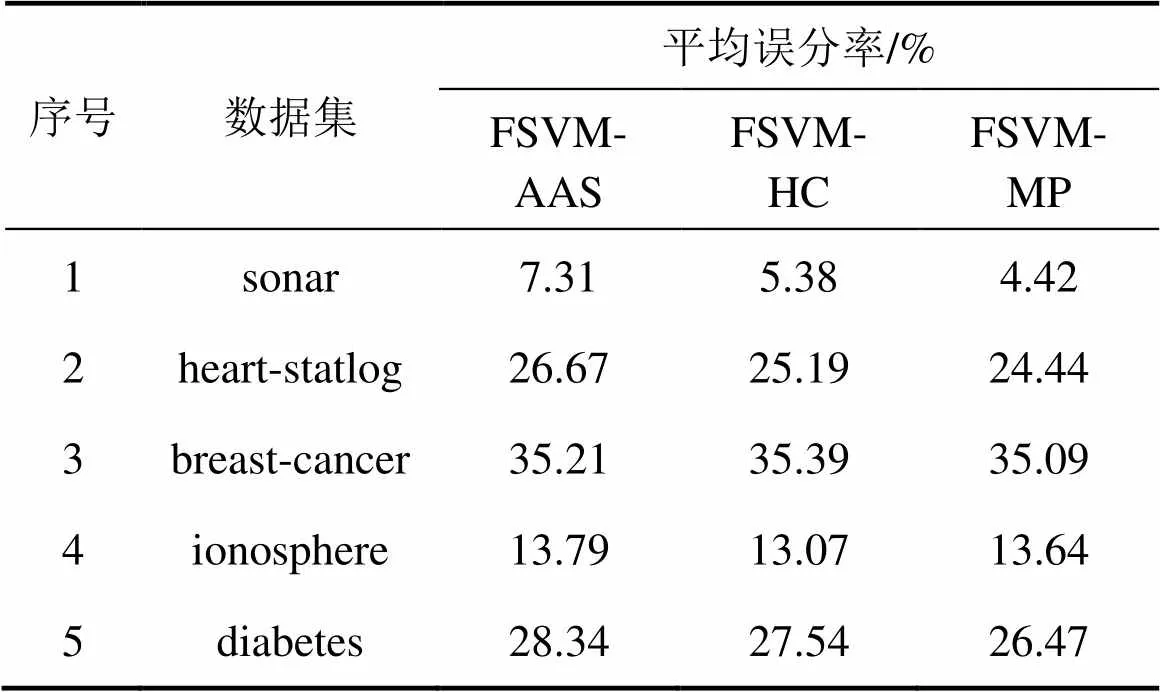
表5 3种方法在真实数据集上的分类结果
由表5可知:各方法平均误分率与样本的特征数相关,对高维数据集(如sonar),3种方法整体上都表现出了较低的误分率,而低维数据集(如breast-cancer和diabetes)的情形则相反。在3种方法的比较中,本文提出的FSVM-MP在真实数据集上获得了相对较低的误分率,泛化能力较好,从而验证了本文方法在真实数据集上的合理性。
4 结论
1) 通过对现有隶属度分配方法的研究,本文提出了一种基于多区域划分的FSVM方法,在构造隶属度函数时,通过建立预置超平面和超球模型,将样本空间划分成多个区域,能够为超球外的野值分配较低的隶属度,同时也能为预置超平面附近的支持向量分配较高的隶属度。
2) 本文提出的方法要优于基于紧密度以及基于类内超平面的方法,具有更好的抗噪性能。
3) 由于在确定控制参数时本文只是参考了隶属度函数的变化情况,如何给出合理的指标以优化控制参数的选取,有待于进一步的研究。
[1] Vapnik V N. Statistical learning theory[M]. New York: John Wiley & Sons, 1998: 52−98.
[2] Lin C F, Wang S D. Fuzzy support vector machines[J]. IEEE Transactions Neural Networks, 2002, 13(2): 464−471.
[3] Atefeh D A, Hui M, Tapan K S, et al. Application of fuzzy support vector machine for determining the health index of the insulation system of in-service power transformers[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2013, 20(3): 965−973.
[4] An W J, Liang M G. Fuzzy support vector machine based on within-class scatter for classification problems with outliers or noises[J]. Neurocomputing, 2013, 110(6): 101−110.
[5] Arindam C, Kajal D. Fuzzy support vector machine for bankruptcy prediction[J]. Applied Soft Computing, 2011, 11(2): 2472−2486.
[6] Abdulhamit S. Medical decision support system for diagnosis of neuromuscular disorders using DWT and fuzzy support vector machines[J]. Computers in Biology and Medicine, 2012, 42(8): 806−815.
[7] Huang H P, Liu Y H. Fuzzy support vector machines for pattern recognition and data mining[J]. International Journal of Fuzzy Systems, 2002, 4(3): 826−835.
[8] 张翔, 肖小玲, 徐光祐. 基于样本之间紧密度的模糊支持向量机方法[J]. 软件学报, 2006, 17(5): 951−958. ZHANG Xiang, XIAO Xiaoling, XU Guangyou. Fuzzy support vector machine based on affinity among samples[J]. Journal of Software, 2006, 17(5): 951−958.
[9] 艾延廷, 费成巍, 王志. 基于改进模糊SVM的转子振动故障诊断技术[J]. 航空动力学报, 2011, 26(5): 1118−1123. AI Yanting, FEI Chengwei, WANG Zhi. Technique for diagnosing fault of rotor vibration based on improved fuzzy SVM[J]. Journal of Aerospace Power, 2011, 26(5): 1118−1123.
[10] 陶新民, 徐晶, 杜宝祥, 等. 基于紧密度FSVM新算法及在故障检测中的应用[J]. 振动工程学报, 2009, 22(4): 418−424. TAO Xinmin, XU Jing, DU Baoxiang, et al. A FSVM based on affinity and its application in bearing fault detection[J]. Journal of Vibration Engineering, 2009, 22(4): 418−424.
[11] 秦传东, 刘三阳. 基于数据域描述的模糊临近支持向量机算法[J]. 系统工程与电子技术, 2011, 33(2): 449−463. QIN Chuandong, LIU Sanyang. Fuzzy proximal support vector machine based on data domain in description[J]. Systems Engineering and Electronics, 2011, 33(2): 449−463.
[12] 郭秩维, 费成巍, 白广忱. 基于FSVM改进隶属度的发动机振动性能分析[J]. 推进技术, 2013, 34(2): 263−268. GUO Zhiwei, FEI Chengwei, BAI Guangchen. Improved fuzzy membership method in FSVM for aeroengine vibration performance fusion analysis[J]. Journal of Propulsion Technology, 2013, 34(2): 263−268.
[13] 唐浩, 廖与禾, 孙峰, 等. 具有模糊隶属度的模糊支持向量机算法[J]. 西安交通大学学报, 2009, 43(7): 40−43.TANG Hao, LIAO Yuhe, SUN Feng, et al. Fuzzy support vector machine with a new fuzzy membership function[J]. Journal of Xi’an Jiaotong University, 2009, 43(7): 40−43.
[14] Ding S F, Gu Y X. A fuzzy support vector machine algorithm with dual membership based on hypersphere[J]. Journal of Computational Information Systems, 2011, 7(6): 2028−2034.
[15] 吴青, 刘三阳, 杜喆. 基于边界向量提取的模糊支持向量机方法[J]. 模式识别与人工智能, 2008, 21(3): 332−337. WU Qing, LIU Sanyang, DU Zhe. Fuzzy support vector machine method based on border vector extraction[J]. Pattern Recognition and Artificial Intelligence, 2008, 21(3): 332−337.
[16] Mao Yong, Xia Zheng, Yin Zheng, et al. Fault diagnosis based on fuzzy support vector machine with parameter tuning and feature selection[J]. Chinese Journal of Chemical Engineering, 2009, 15(2): 233−239.
[17] Hao P Y, Chiang J H, Lin Y H. A new maximal-margin spherical-structured multi-class support vector machine[J]. Applied Intelligence, 2009, 30(2): 98−111.
[18] Tax D M J, Dain R P W. Support vector data description[J]. Machine Learning, 2003, 54(1): 45−66.
[19] 蒋玲莉, 刘义伦, 李学军, 等. 基于SVM与多振动信息融合的齿轮故障诊断[J]. 中南大学学报(自然科学版), 2010, 41(16): 2184−2188. JIANG Lingli, LIU Yilun, LI Xuejun, et al. Gear fault diagnosis based on SVM and muti-seneor information fusion[J]. Journal of Central South University (Science and Technology), 2010, 41(16): 2184−2188.
[20] Murphy P M, Aha D W. UCI repository of machine learning database[EB/OL]. [2013−10−30]. http://www.ics.uci.edu/ mlearning/MLRepository.html.
Fuzzy support vector machine method based on multi-region partition
ZHA Xiang, NI Shihong, ZHANG Peng
(College of Aeronautics and Astronautics Engineering, Air Force Engineering University, Xi’an 710038, China)
Considering that current fuzzy support vector machine(FSVM) can’t effectively locate support vectors and thus causes loss of classified information, a FSVM method based on multi-region partition was proposed. As approximate estimation of FSVM support vectors, the general position of support vectors was obtained with traditional SVM, which further fuses the support vector domain description with negative examples(SVDD-neg) model to divide the whole sample space. The results show that the fuzzy membership is determined according to the position of samples in space by different rules, which weakens the outliers and increases the membership of support vectors. The proposed method is more robust and can gain a better generalization ability compared with the FSVM based on affinity among samples and the FSVM based on the distance between a sample and its hyperplane within the class.
fuzzy support vector machine; multi-region partition; outliers; support vectors; membership
10.11817/j.issn.1672-7207.2015.05.016
TP181
A
1672−7207(2015)05−1680−08
2014−04−17;
2014−07−18
国家自然科学基金资助项目(61372167) (Project(61372167) supported by the National Natural Science Foundation of China)
查翔,博士研究生,从事飞机故障诊断、人工智能及其应用等研究;E-mail: zha_xiang@126.com
(编辑 赵俊)

