下穿既有桥梁隧道施工风险定量评估方法

陈洁金，张永杰



下穿既有桥梁隧道施工风险定量评估方法

陈洁金1, 2，张永杰1

(1. 长沙理工大学土木与建筑学院，湖南长沙，410004；2. 长沙理工大学岩土工程施工灾变防控与环境修复技术2011协同创新中心，湖南长沙，410004)

以城市隧道下穿建(构)筑物风险定量评估体系为研究对象，针对施工中存在随机和模糊不确定性问题，基于故障树、区间算法和模糊数学建立模糊故障树风险评价模型。首先在调查100多处城市隧道施工不当引起临近建(构)筑物安全事故的案例后，总结风险事故的影响因素和基本事件。其次，根据专家的经验和模拟试验确定基本事件的发生模糊概率，利用模糊区间算法计算顶事件的模糊发生概率和各影响因素的模糊重要度；采用模糊层次评价模型对临近桥梁损害风险发生的后果进行评估，根据顶事件的风险发生概率和风险后果程度确定风险等级。最后结合工程实例，验证该模型的准确性和有效性。研究结果表明：该方法提供了一套完整的下穿建(构)筑物城市隧道施工风险的定量评估体系，可为管理部门风险规避提供参考。

隧道施工；风险；模糊故障树；模糊层次分析

在隧道工程建设中，风险具有多样性和多层次性，时间跨度大，动态变化大，管理难度大。其中对第三方既有设施影响的风险是城市隧道工程风险的重要组成部分。由于缺乏科学风险评估工具和科学的风险管理体系，在现有城市隧道建设过程中，安全事故时有发生。随着城市建筑物越来越多，地下管网越来越密集，工程建设风险也越来越高，也越来越引起人们的重视。在隧道施工过程中，影响临近建筑物损害的因素众多，致灾机制复杂，对其进行预测预报和定量风险评估非常困难[1]。在隧道施工风险评估方面，Sturk等[2]分析了故障树法、危险和可操作性分析法、专家调查法等的适应性，并且将风险分析技术应用于斯德哥尔摩环形公路隧道。Kampmann等[3]运用风险评估技术为哥本哈根地铁工程提出了包括40多种灾害的10种风险类型，并建立了具体的分类体系。Burland等[4]给出了对环境影响的评估方法和程序，并将该研究成果应用于伦敦Jubilee线路延伸工程中。温森等[5]采用概率理论推导了变形引起的TBM风险事故的综合风险概率计算模型。侯艳娟等[6]引入模糊数学综合评判方法对地表建筑物的安全风险进行了分析评估。王景春等[7]综合应用国内外岩土力学研究和测试成果，根据影响隧道施工安全的主要因素及其权重，导出了危险性评价指数模型，建立了海底隧道施工安全的分级体系。以上方法均停留在定性层面上，不能对风险事件的发生概率进行定量评估。故障树分析作为一门重要的逻辑与概率分析方法在系统可靠度分析中得到了广泛应用[8]。在此，本文作者建立模糊故障树模型对风险事件发生概率进行定量评估，并采用模糊层次评价模型对临近建筑物损害风险发生的后果进行评估。

1 基于故障树的模糊区间算法

对于一个给定的故障树，其结构函数可以通过分析得到。在基于布尔代数和概率论的传统故障树分析中，顶事件的发生概率可以通过各底事件的发生概率和结构函数唯一确定。但是，当底事件的发生概率为模糊概率(模糊数)时，顶事件的发生概率也是模糊概率，其隶属函数可以通过模糊数学中的扩展原理获得。然而，采用扩展原理确定顶事件模糊概率的隶属函数的过程事实上是一个数学规划问题，在一般情况下，求解规划的最优解会比较困难，尤其是对于复杂系统，其结构函数非常复杂，维数很高，要精确确定顶事件模糊概率的隶属函数基本上很困难。模糊故障树的研究始创于Hideo[9]，他们将模糊概率替代基本事件的精确概率，并根据模糊数学的扩展原理对顶事件的模糊概率进行研究，模糊数之间的乘积采用近似计算。Singe[10]也对模糊故障树分析作了进一步研究，他主要采用L−R型模糊数来描述，并定义了L−R型模糊数运算法则。Alireza等[11]则提出了一种模糊故障树分析的新方法，先将基本事件的隶属函数离散化，得到每一个基本事件可能性分布的若干区间，然后利用扩展原理定义的max和min算子进行区间运算得到顶事件的可能性分布。Sawyer[12]在研究机械系统模糊故障树分析时，将底事件发生概率视为模糊数，模糊数运算采用区间上的截集运算。这种区间运算与上述扩展原理是等价的。

1.1 模糊数的概念

一般的模糊数用3个参数,和表示，记为=(,,)。其中：为模糊数的均值；和为模糊数的左、右分布参数。若模糊数的隶属函数满足

则称模糊数为L−R型模糊数。工程上常用的L−R型模糊数有三角模糊数、正态型模糊数等[6]。

1.2 模糊数的区间一般算法

设模糊数=(,,),模糊数=(,,)，则模糊数的加法、减法、乘法、除法分别为

1.3 故障树分析的模糊算子

在模糊数的代数运算基础上，可以对故障树的与门和或门进行模糊运算，分别称为与门模糊算子和或门模糊算子。传统的故障树分析中，与门算子为

其中：P为事件的发生概率。若事件发生的概率为一模糊数，则根据模糊理论的扩展原理分别可得：

由经典的FTA可知，假设故障树的全部最小割集为[8]1,2, …,C顶事件发生的概率为

其中：C，C和C分别为第,和最小割集；N为最小割集数。

1.4 扩展原理

1.5 模糊重要度分析

结构重要度分析是从事故障树的结构上分析各基本事件的重要程度。若进一步考虑基本事件发生的变化对顶上事件发生概率的影响程度，则要分析基本事件的概率重要度。概率重要度系数为[13]

其中：()为顶上事件的发生概率；q为第个基本事件的发生概率；I()为第个基本事件的概率重要度系数。关键重要度表示第个基本事件发生概率的变化率引起顶上事件发生概率的变化率，表示为[13]

根据扩展原理，相应地可以得到模糊概率重要度系数和模糊关键重要度系数。

2 工程概况

金沙洲隧道为穿越城区复杂条件下的武广(武 汉—广州)客运专线隧道。该隧道内轮廓采用单洞双线断面，隧道有效内净空面积为100 m2，暗洞开挖面积超过150 m2。下穿广佛立交、广州西环高速公路和建设大道。金沙洲隧道具有地质条件和环境条件非常复杂的特点，其综合难度在国内外都属罕见，技术难度非常大，风险高。

广佛(广州—佛山)立交桥老桥位于广佛高速公路和环城高速公路相交处，1989—06修建完工。1999年进行了拓宽改建，在原桥梁一侧增设桩基础结构梁桥，即B匝道桥。老桥桥梁两侧是简支梁，中间横跨环城高速公路段为两跨连续梁结构。桥梁纵向方位近东西走向，而隧道呈近南北走向，金沙洲隧道中线与广佛立交桥中线在隧道里程DK2194+675.7处斜交，角度为83°5′45″。B匝道桥是既有广佛立交增加车道而新建的简支梁桥，采用桩基础，桥面与广佛立交相连接而形成整体[1]，见图1。

图1 金沙洲隧道与广佛立交桥平面关系图

3 风险事件模糊概率计算

3.1 故障树的建立

隧道的开挖引起地层移动和变形过大，从而引起建(构)筑物的变形超过建(构)筑物的剩余变形而引起破坏。将金沙洲隧道施工引起广佛立交变形破坏的风险事件作为故障树的顶事件。这个事件发生的直接原因是隧道开挖引起地层移动、地层作为传播介质将变形传给广佛立交以及广佛立交抗剩余变形能力较小等。将广佛立交抗变形能力作为条件事件，若广佛立交抗变形大于地层变形，则广佛立交不会引起破坏。根据隧道施工引起上覆建(构)筑物变形特点，构建广佛立交变形破坏故障树模型，见图2。

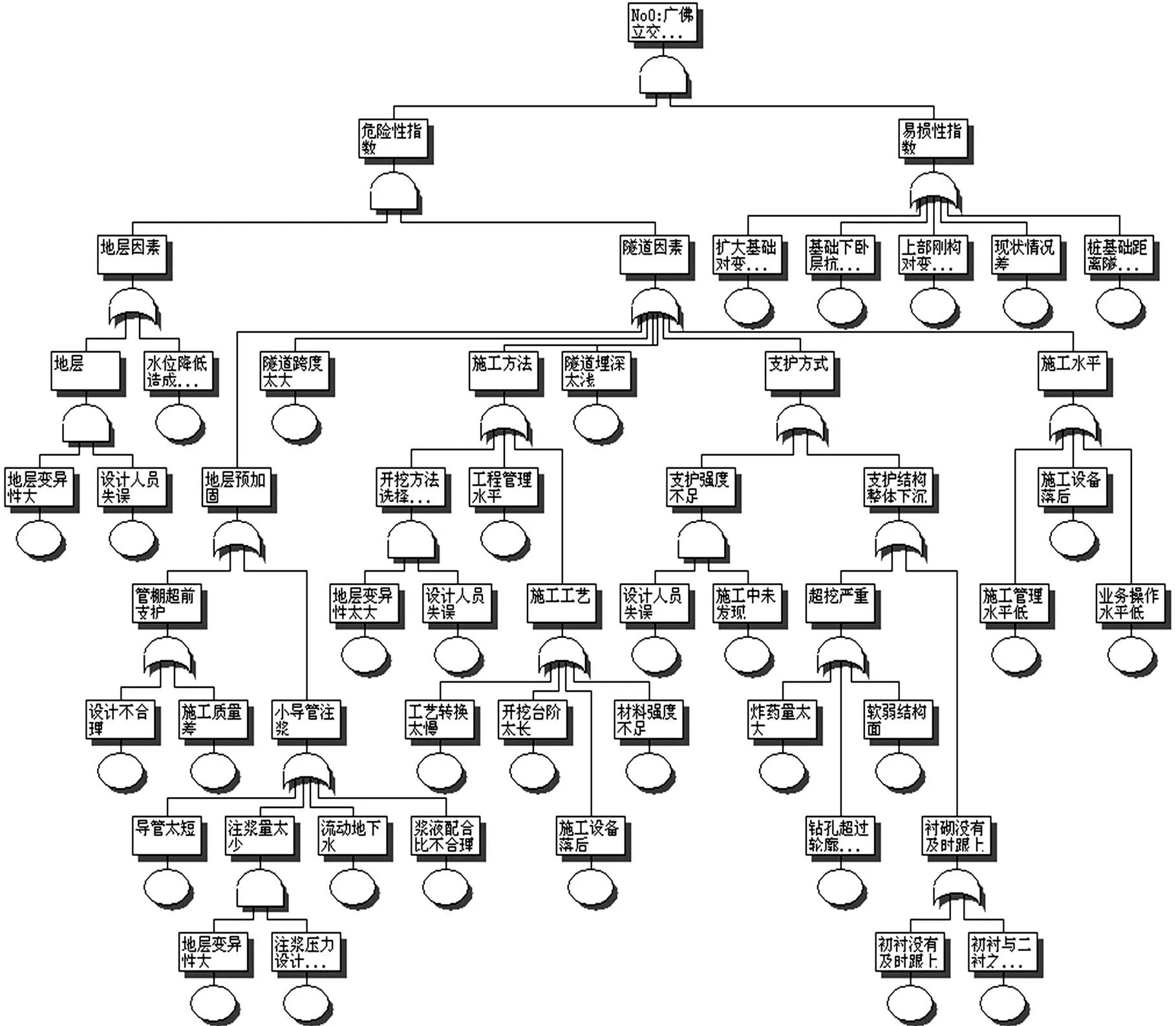
图2 广佛立交变形破坏故障树模型

3.2 基本事件的模糊数

建筑(构)物变形破坏故障树的分析计算中，导致系统失效(顶事件)的底部基本事件发生原因复杂，由于缺乏足够的现场数据及实验数据并受环境的变化和事物发展的不稳定性等因素的影响，很难确定其发生概率的准确值，这便使得传统的故障树分析方法很难适用，必须应用模糊数学中的相关理论和方法来解决。通过调查100多处城市隧道施工不当引起临近建(构)筑物安全事故的案例后，得到不完全统计数据，再结合专家打分的办法对不确定因素进行评价。根据Foster等[14]提供的各种定性描述表判断各种因素对事件的影响，然后对照表1对故障树各项基本事件的影响转换成概率。为了尽可能准确地描述事故发生的可能性，人们通常采用三角模糊数、梯形模糊数、L−R模糊数、正态模糊数等模糊数作为底事件的模糊发生概率。文献[15]介绍了几种模糊故障树分析法。

表1 事件发生概率[15]

本文采用其中较易计算的三角模糊数来表征底事件发生概率。由于三角模糊数计算既简单又具有代表性，采用三角模糊数表征基本事件发生的概率。根据各个基本事件的概率统计数据，取其中值作为，结合工程技术人员的实际经验和判断，给出的左右扩展模糊数和及基本事件模糊概率，见表2。

表2 基本事件发生概率的三角模糊数

3.3 顶事件的模糊数计算

根据前面所述的模糊数区间运算法则，用模糊数的减法运算和乘法运算分别代替普通概率的减法和乘法运算，将上述基本事件和条件事件的模糊概率代入式(5)，运用CAFTA故障树分析系统即可计算得到顶事件发生的模糊概率，其仍可以用三角模糊数近似表示，其值为(0.114，0.258，0.432)。其中危险性指数的模糊概率为(0.347，0.486，0.611)，易损性指数的模糊概率为(0.328，0.529，0.701)。

对重要度进行分析，结果见文献[1]。在所有底事件中，地下水的流失造成地层损失对危险性指数的影响最明显。在建筑物易损性评价中，基础下卧层抗变形能力和上部结构的变形敏感性的影响最明显。在施工过程中，可以首先考虑采取相应措施来降低这些底事件的发生概率，因为这样容易降低“顶事件”的发生概率。

4 风险事件后果的模糊层次分析

根据模糊层次分析方法对“广佛立交变形破坏”风险事件后果进行评价，具体步骤如下[16]。

1) 建立因素集。参考《铁路隧道风险评估与管理暂行规定》，“广佛立交变形破坏”事件的后果评价因素分为4个：经济损失、人员伤亡、工期延误和环境影响。

各种后果的评价标准划分为5个等级：灾难性的、很严重的、严重的、较大的和轻微的。

2) 建立评价集：

3) 层次分析确定因素权重。

①建立递阶层次结构。一个好的层次结构对于风险分析是极为重要的，要确保层次的划分和层次之间的支配关系清晰和合理。

②构造两两比较判断矩阵。采用刘保国等[17]提出的评判准则，得出各层次的判断矩阵，见表3。

表3 判断矩阵

用和积法计算上述矩阵的最大特征根及其的特征向量。

第1步，得到正规化判断矩阵为

第2步，按行相加得：

；

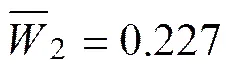
则所求得特征向量为

；

。

第5步，计算一致性系数R：

4) 确定隶属度，建立等级评价矩阵。现由10名专家参加评估，其具体的分类、权重和评估结果如表4所示。

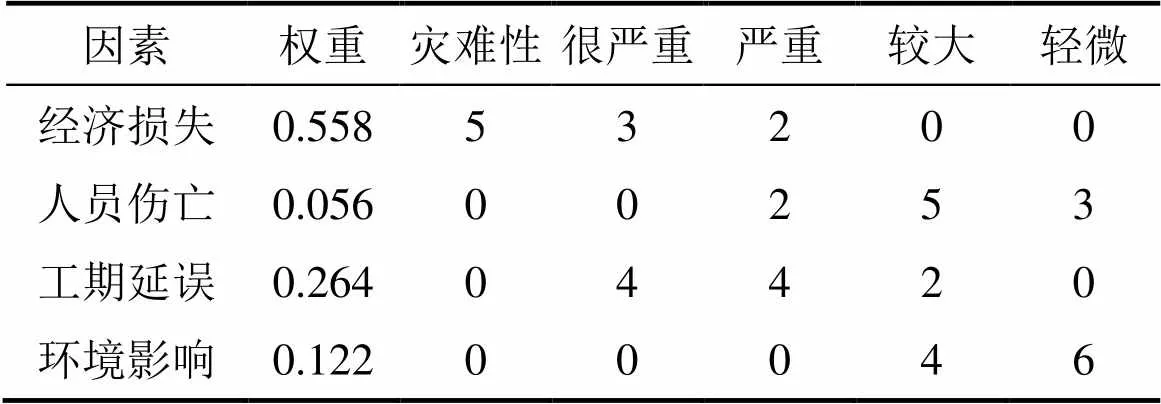
表4 专家打分评价矩阵

由上述专家打分可得到等级评价矩阵：

5) 模糊综合评价：

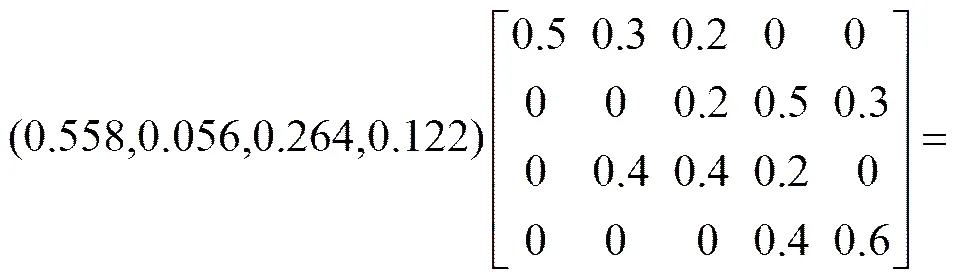
6) 评价结论。为了充分利用模糊评价矩阵中的信息，采用等级评分办法确定“广佛立交变形破坏”风险事件后果的等级。具体得分等于分值乘以权重，总分等于3.521，见表5。

表5 等级评分

5 风险等级综合评定

“广佛立交变形破坏”风险事件的模糊发生概率为(0.114，0.258，0.432)。事件后果的模糊值在(严重，很严重)之间。参考《铁路隧道风险评估与管理暂行规定》判别风险等级级别。得到“广佛立交变形破坏”风险事件的风险等级为(高度，极高)之间，具体见表6。风险评价结果与委托专业勘察单位勘察结果基本吻合，验证了该风险评价方法准确性与科学性。

表6 风险等级

针对“广佛立交变形破坏”风险事件，由模糊评估方法所得结论与由综合风险指数评估方法所得结论是一致的，风险等级为高到极高，相互验证了该方法的正确性和实用性。隧道施工综合指数模型快速、简洁，而模糊评估方法是一种定量评估方法，针对风险事件的发生概率和后果可以对底事件进行3种概率重要度分析，容易采取降低风险的措施。

6 结论

1) 基于故障树分析理论，建造“广佛立交变形破坏”故障树模型，通过计算得到了顶事件的模糊发生概率和底事件的3种重要度，并对隧道施工引起上覆桥梁变形破坏的风险事件进行了定性分析和定量分析。通过对重要度进行分析容易找到降低风险的措施。

2) “广佛立交变形破坏”风险事件的模糊发生概率取决于底事件发生概率的准确性，底事件发生概率依赖于数据统计，本文在没有数据的情况下，采用专家经验和模拟试验数据。

3) 综合考虑“广佛立交变形破坏”风险事件的模糊发生概率和事故后果的模糊严重程度，得到该事件的风险等级。故障树模型是在系统理论的基础上建立的，风险等级的划分有科学依据，结合工程实例论证了该方法的准确性和有效性。

[1] 陈洁金. 下穿既有设施隧道城市隧道施工风险管理与系统开发[D]. 长沙: 中南大学土木与建筑学院, 2009: 1−3. CHEN Jiejin. Risk management and system development of city tunnel construction underpassing existing facilities[D]. Changsha: Central South University. School of Civil Engineering and Architecture, 2009: 1−3.

[2] Sturk R, Olsson L, Johansson J. Risk and decision analysis for large underground projects as applied to the Stockholm ring road tunneling[J]. Tunneling and Underground Space Technology, 1996, 11(2): 157−164.

[3] Kampmann J, Eskesen S D, Summers J W. Risk assessment helps select the contractor for the Copenhagen metro system[C]// Proceedings of the World Tunnel Congress 98 on Tunnels and Metropolises. Sao Paolo, Brazil, 1998: 123−128.

[4] Burland J B, Standing J R, Jarding F M. Building response to tunneling: Case studies from construction of the Jubilee line extension, London[M]. Thomas Telford Publishing, 2001: 156−159.

[5] 温森, 贺东清, 杨圣奇. 隧洞变形引起的TBM施工事故综合风险分析[J]. 岩土力学, 2014, 35(6): 1727−1734. WEN Sen, HE Dongqing, YANG Shengqi. Comprehensive risk analysis of TBM construction accident induced by tunnel deformations[J]. Rock and Soil Mechanics, 2014, 35(6): 1727−1734.

[6] 侯艳娟, 张顶立. 浅埋大跨度隧道穿越复杂建筑物安全风险分析与评估[J]. 岩石力学与工程学报, 2007, 26(增2): 3719−3726. HOU Yanjuan, ZHANG Dingli. Safety risk analysis and assessment of shallow large span tunnel through complex building[J]. Rock Mechanics and Engineering, 2007, 26(Suppl 2): 3719−3726.

[7] 王景春, 侯卫红, 莫勋涛. 海底隧道施工安全评价的初步研究[J]. 岩石力学与工程学报, 2007, 26(增2): 3757−3764.WANG Jingchun, HOU Weihong, MO Xuntao. A preliminary study of tunnel construction safety assessment[J]. Rock Mechanics and Engineering, 2007, 26(Suppl 2): 3757−3764.

[8] 刘东. 动态故障树分析方法[M]. 北京: 国防工业出版社, 2013: 36−39. LIU Dong. Dynamic fault tree analysis method[M]. Beijing: National Defense Industry Press, 2013: 36−39.

[9] Hideo T. Fuzzy-tree analysis by fuzzy probability[J]. IEEE Transaction on Reliability, 1983, 232(5): 256−259.

[10] Singe D. Fuzzy set approach to fau1ttree and reliability analysis[J]. Fuzzy Set and Systems, 1999, 34(2): 145−155.

[11] Alireza E, Seyed G M. FPGA-based Monte Carlo simulation for fault tree analysis[J]. Microelectronics and Reliability, 2004, 44(6): 1017−1028.

[12] Sawyer J P. Fault tree analysis of mechanical systems[J]. Microelectronics and Reliability, 1994, 54(4): 653−667.

[13] 陈洁金, 阳军生, 刘宝琛. 岩溶地面塌陷风险分析的模糊故障树模型[J]. 湖南大学学报(自然科学版), 2008(35): 58−61.CHEN Jiejin, YANG Junsheng, LIU Baochen. Karst collapse risk analysis fuzzy fault tree model[J]. Journal of Hunan University (Natural Science), 2008(35): 58−61.

[14] Foster M A, Fell R, Davidson R, et al. Estimation of the probability of failure of embankment dams by internal erosion and piping using event tree methods[C]// ANCOLD: Australian National Committee of the International Commission on Large Dams Conference on Dams. Sydney, Austriala, 2001: 45−46.

[15] 周峰. 山岭隧道塌方风险模糊层次评估研究[D]. 长沙: 中南大学土木工程学院, 2008: 45−49. ZHOU Feng. Study of mountain tunnel collapse fuzzy risk assessment[D]. Changsha: Central South University. School of Civil Engineering, 2008: 45−49.

[16] 许振浩, 李术才, 李利平, 等. 基于层次分析法的岩溶隧道突水突泥风险评估[J]. 岩土力学, 2011, 32(6): 1757−1766. XU Zhenhao, LI Shucai, LI Liping, et al. Risk assessment of water or mud inrush of Karst tunnels based on analytic hierarchy process[J]. Rock and Soil Mechanics, 2011, 32(6): 1757−1766.

[17] 刘保国, 沈铭龙, 马强. 模糊网络分析法在公路山岭隧道施工风险分析中的应用[J]. 岩石力学与工程学报, 2014, 33(增1): 2861−2866. LIU Baoguo, SHEN Minglong, MA Qiang. Application of fuzzy analytic network process in risk analysis for construction of highway mountain tunnel[J]. Rock Mechanics and Engineering, 2014, 33(Suppl 1): 2861−2866.

Quantitative risk assessment model of tunnel construction under passing existing bridges

CHEN Jiejin, ZHANG Yongjie

(1. School of Civil Engineering and Architecture, Changsha University of Science and Technology, Changsha 410004, China;2. Geotechnical Engineering Disaster Prevention and Environmental Remediation Technology of 2011 Collaborative Innovation Center, Changsha University of Science and Technology, Changsha 410004, China)

The quantitative risk assessment system of city tunnel construction underpassing existing bridges was studied. Considering the presence of random and fuzzy uncertainties in city tunnel construction, a fuzzy fault tree risk assessment model was set up based on the fault tree, interval algorithm and fuzzy math. Firstly, the main influence factors and corresponding risk basis event were summarized on the basis of the investigation of more than 100 cases about accidents caused by the tunnel improper construction adjacent buildings and constructs. Secondly, the fuzzy probability of basic events was determined according to experts’ experience and simulation tests, and the fuzzy probability of adjacent buildings damages and the fuzzy important degree of each factor were obtained through the interval algorithm. Furthermore, the consequence of damaging risks of the adjacent bridges was evaluated by fuzzy hierarchical evaluation model. Finally, the engineering example was analyzed to identify the correctness and effectiveness of this method. The results show that the method provides a complete assessment system for city tunnel construction underpassing existing bridges, and it provides important reference on risk avoidance for risk management institute.

tunnel construction; risk; fuzzy fault tree; FAHP analysis

10.11817/j.issn.1672-7207.2015.05.039

O319.56

A

1672−7207(2015)05−1862−07

2014−08−08；

2014−10−12

国家自然科学基金资助项目(51208063) (Project(51208063) supported by the National Natural Science Foundation of China)

陈洁金，博士，从事隧道与地下工程风险、工程地质及超前地质预报等研究与教学工作；E-mail: chenjjin1975@163.com

(编辑 陈灿华)