基于伽马过程的锈蚀钢筋混凝土桥梁检测维护策略优化

黄天立，周浩，王超，任伟新，陈华鹏



基于伽马过程的锈蚀钢筋混凝土桥梁检测维护策略优化

黄天立1，周浩1，王超2，任伟新1，陈华鹏3

(1. 中南大学土木工程学院，湖南长沙，410075；2. 湖北工业大学土木工程与建筑学院，湖北武汉，430068；3. 英国格林威治大学土木工程系，Chatham Maritime, Kent, ME4 4TB，London, UK)

针对考虑钢筋锈蚀的钢筋混凝土桥梁结构，将钢筋局部锈蚀深度作为表征结构使用性能的退化指标，采用Gamma过程模拟其发展过程的不确定性；给出考虑钢筋锈蚀检测概率和维护措施的结构使用寿命预测模型和基于决策维护树模型的检测维护成本计算模型；以最大化桥梁经检测维护后的使用寿命期望和最小化检测维护成本为优化目标函数，提出基于Gamma过程和遗传算法的锈蚀钢筋混凝土桥梁结构检测维护策略优化分析方法。分析广西铁山港大桥钢筋混凝土30 m跨主梁，得到其检测维护策略的Pareto优化解集。研究结果表明：Pareto优化解集可提供在不同结构使用寿命期望和检测维护成本预算下收益最大的检测维护策略，为业主或土木基础设施管理部门提供决策依据。

钢筋混凝土桥梁；钢筋锈蚀；检测维护策略优化；Gamma随机过程；遗传算法

钢筋混凝土桥梁等土木基础设施结构在长期运营过程中，在荷载和环境等因素的作用下不可避免地将产生性能退化，为保证其长期安全运营和耐久性，需要对其进行必要检测和维护。目前，一般来说，在桥梁等土木基础设施结构投入运营前即制定了定期检测和维修等维护计划以保证桥梁的安全使用性能和耐久性，这种检测维护策略常常由于检测维护资金不到位使得结构的安全性存在隐患，或者由于结构的安全状况较好，但预定的检测和维护措施过多造成检测维护资金浪费，因而具有一定的局限性。因此，如何高效地利用有限资金对量大面广的土木基础设施结构进行合理检测和维护，即在合适的时间以最少的经济成本进行检测和维护以达到延长结构使用寿命等社会收益的最大化，是业主和土木基础设施管理者们迫切关心的问题[1−2]。在过去20 a中，国内外许多学者针对退化的钢筋混凝土结构的提出了许多优化维护方法。Ellingwood等[3]针对退化的核电站钢筋混凝土结构，以时变可靠度为结构状态指标，以全寿命周期成本最小为优化目标函数，提出了优化的检测维修措施。Enright等[4]针对退化的混凝土桥梁结构，基于给定的可靠度约束，以期望的成本最小为优化目标函数，给出了优化的维护策略。Stewart[5]针对腐蚀引起的钢筋混凝土结构裂缝程度，给出了考虑维修和检测间隔的全寿命周期成本和维护成本计算公式，并比较了2种维护措施对钢筋混凝土桥面板维护成本的影响。van Noortwijk等[6]采用Gamma过程模拟结构使用性能退化过程，以等效平均维护成本为目标函数，对不同结构的检测维护措施进行优化。特别地，Frangopol[1]对近年来提出的不确定性条件下基于概率的全寿命周期性能、管理和维护优化方法等进行了详细综述。国内也有许多学者从事相关研究工作，如：秦权[7]基于时变可靠度，提出了桥梁检测与维修方案的优化方法，其最优检测与维修方案在保证桥梁可靠度指标在全寿命期大于容许限值的基础上，使全寿命期的总费用最小；杨伟军等[8]提出了以动态可靠性为约束，以维修加固费用和失效损失之和为目标函数的服役桥梁维修加固决策策略模式。邵旭东等[9]针对桥面板铺装结构，提出了基于可靠度指标的优化维护策略。一般来说，维护措施在检测完成之后进行。检测的结果可用来判断损伤是否存在、损伤的程度以及需要采取何种维护措施，因此，应将检测和维护策略综合考虑。Kim 等[10]针对退化的钢筋混凝土结构，以最大化延长结构的使用寿命和最小化结构期望成本为优化目标函数，提出了基于概率的优化检测维修规划方法并将其应用于既有桥梁结构。周浩等[11]针对考虑钢筋锈蚀的钢筋混凝土桥梁结构，以最大化桥梁经检测维护后的使用寿命和最小化检测维护成本为优化目标函数，提出了基于概率的锈蚀钢筋混凝土桥梁结构检测维护策略优化分析方法，得到了其检测维护策略的Pareto优化解集。本文作者针对考虑钢筋锈蚀的钢筋混凝土桥梁结构，将钢筋局部锈蚀深度作为表征结构使用性能的退化指标，采用Gamma过程模拟其发展过程的不确定性；给出考虑钢筋锈蚀检测概率和维护措施影响的结构使用寿命预测模型和基于决策维护树模型的检测维护成本计算模型；以最大化桥梁经检测维护后的使用寿命期望和最小化检测维护成本为优化目标函数，提出基于Gamma过程和遗传算法的锈蚀钢筋混凝土桥梁结构检测维护策略优化分析方法。算例分析了广西铁山港大桥钢筋混凝土30 m跨主梁，得到其检测维护策略的Pareto优化解集。

1 基于Gamma过程的钢筋局部锈蚀深度发展过程模拟

1.1 钢筋局部锈蚀深度发展过程

钢筋混凝土桥梁结构中钢筋锈蚀主要由混凝土碳化和氯离子侵蚀造成[12]。混凝土碳化是指由于混凝土中的Ca(OH)2与环境中的CO2等酸性物质中和导致混凝土的pH降低，钢筋表面钝化膜所需的碱性环境被破坏，钢筋即开始锈蚀。氯离子侵蚀主要是由于氯离子作为一种高效活化剂，较小剂量的氯离子即可破坏钢筋表面的钝化膜，使钢筋在环境因素的作用下开始出现锈蚀。钢筋锈蚀使混凝土中钢筋的净截面面积减小，产生的锈蚀物使得钢筋体积膨胀，对混凝土产生环向应力而使混凝土受拉。此外，疏松的锈蚀层降低了钢筋与混凝土之间的黏结程度，进而降低构件的承载力和延性，改变结构破坏模式，影响结构耐久性。本文仅考虑氯离子侵蚀引起的钢筋锈蚀。

钢筋锈蚀可分为均匀锈蚀(general corrosion)和局部锈蚀(pitting corrosion)。均匀锈蚀是将钢筋的锈蚀视为截面面积均匀减小；局部锈蚀则认为锈蚀的发生和发展是随机的，不同区域出现的锈蚀程度是随机分布的。钢筋的局部锈蚀可用图1所示模型表示[13]，锈蚀后钢筋的剩余截面积r()可表示为

其中：

式中：corr为钢筋锈蚀速率(mm/a)；为钢筋坑蚀系数，一般介于4~8之间；为钢筋锈蚀开始出现的时间(a)；max为钢筋最大局部锈蚀深度(mm)；average为钢筋均匀锈蚀深度(mm)；p为钢筋保护层厚度(mm)；c为氯离子扩散系数(mm2/a)；为混凝土表面氯离子质量浓度(kg/m3)；为氯离子临界质量浓度(kg/m3)；erf为高斯误差函数。研究表明[14]：当钢筋内腐蚀电流强度为corr=1 μA/cm2时，钢筋锈蚀速率corr=11.6 μm/a。

1.2 基于Gamma过程的钢筋局部锈蚀深度发展过程模拟

由于影响钢筋锈蚀的各种因素(如钢筋锈蚀速率、钢筋坑蚀系数和钢筋锈蚀开始出现时间等)具有不确定性，通常将这些影响因素作为随机变量，并假设其概率分布和均值、变异系数，通过Monte Carlo模拟得到钢筋锈蚀发展过程的概率均值和变异系数[11]。在实际工程结构中，获取影响钢筋锈蚀各种因素的随机概率分布比较困难，因此，本文考虑采用Gamma随机过程直接模拟钢筋局部锈蚀深度的发展过程。

Gamma随机过程是一种考虑独立、非负退化增量的随机过程，适合模拟具有微小增量的累计渐变过程，如疲劳、锈蚀和蠕变等[6]。假设结构某时刻使用性能的累计退化量满足Gamma分布，其概率密度函数a为

式中：a为Gamma分布的概率密度函数；和分别为Gamma分布的形状参数和尺度参数；当＞0时，为Gamma函数；表示右连续、单调递增且恒大于0的退化增长方程，且有。对于任意时间间隔内的累计退化量，具有以下性质[6]：

式中：t+1＞t＞0。

对于特定的退化过程，式(8)中通常为已知，未知参数和可采用最大似然估计法进行估计。假设观测到的结构退化增量为

其似然函数为

(11)

1) 根据已知经验公式对时刻时累计退化量()进行取样。

2) 根据起、始时刻累计退化量计算得到中间时刻累计退化量(/2)，其中已知时刻时累计退化量，/2时刻累计退化量的条件分布为

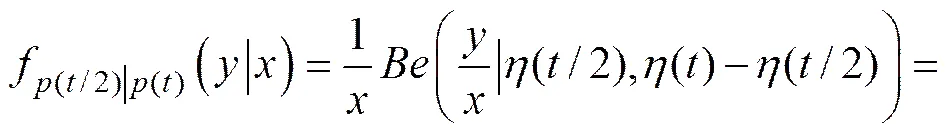
式中：(∙)为区间[0,1]上的Beta分布。

3) 根据(0)，(/2)和()分别计算(/4)和(3/4)；

2 考虑钢筋锈蚀检测概率和维护措施影响的桥梁使用寿命预测

2.1 钢筋锈蚀的检测概率

为了表示钢筋锈蚀对钢筋混凝土结构使用性能的退化程度，采用时刻钢筋局部锈蚀深度()与钢筋初始直径0的比值即结构损伤强度指标[11]表征：

式中：()为时刻钢筋的局部锈蚀深度(mm)；0为钢筋的初始直径(mm)。

设定结构损伤强度指标的限值，根据损伤检测结果，针对不同的损伤强度确定结构是否需要维护以及采用不同类型的维护措施。常用的桥梁检测手段包括现场肉眼观察、无损检测等手段，不同的检测方法其检测质量不一样，意味着某些程度的损伤并不能被某一检测方法所检测到。结构的损伤能否被检测到与损伤检测方法的识别概率和损伤发展程度有关，本文采用对数损伤检测概率公式进行描述[16]：

式中：oD为损伤检测概率；为结构损伤强度指标；为检测方法能检测到的最小损伤强度指标，其定义为oD=0.001时的损伤强度指标；为表征检测方法优劣的量纲为1的参数；是1个与相关的尺度参数，对于钢筋混凝土结构中锈蚀损伤，可取=0.1ln；为标准正态分布函数。

：1—0.1；2—0.3；3—0.5

2.2 考虑钢筋锈蚀检测概率和维护措施影响的桥梁使用寿命预测

Torres-Acosta 等[17]指出，钢筋混凝土构件的使用寿命可以根据下式进行预测：

式中：average为钢筋平均锈蚀深度(mm)；0为钢筋初始直径(mm)；life为取值介于0.035~0.080之间的量纲为1的参数。由式(4)和式(15)即可得到钢筋局部最大锈蚀深度为

给定钢筋局部锈蚀深度累积量阈值thres，钢筋局部最大锈蚀深度达到阈值的时间即为结构的使用寿命。图3所示为无维护和2种不同类型维护措施情况下，结构性能退化发展过程和结构使用寿命的影响曲线。图3中：life0，life1和life2分别表示无维护措施、采取第1种和第2种检测维护措施时结构的使用寿命。第1种维护措施的维护效果用损伤发展延迟时间eff表示，在eff时间段内，结构的使用性能保持不变，之后其使用性能仍按初始趋势退化，当退化累积量达到阈值thres时，此时桥梁的使用寿命为life1；第2种维护措施的维护效果表示桥梁经过维护后，其使用性能退化累积量可被降低到较低的水平maint，之后其使用性能仍按初始趋势退化，当退化累积量达到阈值thres时，此时桥梁的使用寿命为life2。

考虑钢筋锈蚀检测的不确定性，桥梁结构经过检测和采取相应的维护措施后，其使用寿命可表示为

式中：life,i为采用第种维护措施之后的结构使用寿命；oD为ins时刻所采用的检测方法的检测概率。

3 基于检测维护决策树模型的桥梁全寿命周期检测维护成本

在实际的桥梁检测、维护工作中，不仅要考虑检测和维护的效果，而且需要考虑所采取的检测和维护成本。检测和维护效果好的方法能够更好地提高桥梁结构的使用性能，但所需支出的成本也会相应地增加。

桥梁全寿命周期内的检测维护成本包括检测成本、维护成本和失效成本。

1) 检测成本。检测成本又可以分为初步检测成本和深入检测成本。仅考虑单位桥梁检测，初步检测成本与检测方法的精确度有关，初步检测成本可根据下式计算[10]：

式中：insp和ins为常量；为表征检测方法优劣的量纲为1的参数。深入检测以便进一步确定结构的损伤程度，其成本可视为常量。

2) 维护成本。根据维护效果，维护成本也不尽相同，其可表示为维护效果的函数：

式中：表示不同维护措施的维护效果无量纲参数。值越大，表示维护效果越好，维护成本也越高。

3) 失效成本。失效成本主要与经过检测维护之后结构的使用时间有关，可根据下式计算：

式中：risk为常量，表示结构使用寿命达到预期使用寿命时的损失；life0为桥梁初始预测使用寿命；life1为经过检测维护之后的桥梁预测使用寿命。

考虑钢筋锈蚀检测的不确定性，桥梁结构经过检测和采取相应的维护措施后，其寿命周期内的检测维护总成本total可表示为

采用不同的检测维护策略，桥梁具有不同的使用寿命和不检测维护总成本。图4所示为检测维护策略的决策树模型，其中每一个分支表示一类检测维护策略，并由此确定相应的桥梁最终使用寿命和检测维护成本。

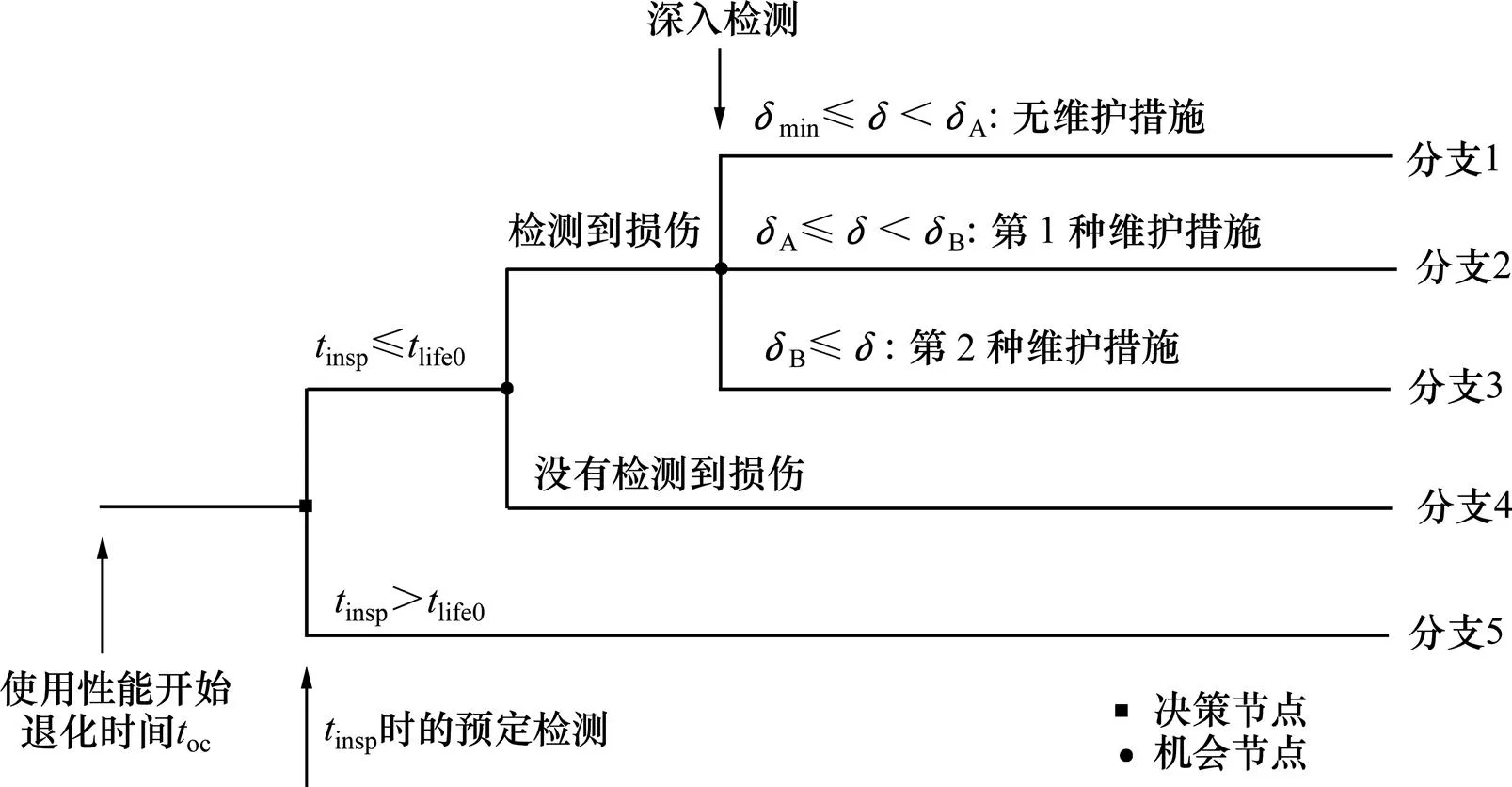
图4 桥梁检测维护决策树模型

分支1：初步检测时间在结构初始使用寿命以内且检测到结构存在损伤，经深入检测后可知，结构的损伤程度大于检测方法所能检测的最小检测损伤程度且小于决策区间下限，此时无需采取维护措施。由此得到的桥梁最终使用寿命和检测维护成本下式计算：

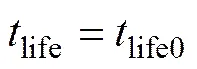
分支2：初步检测时间在结构初始使用寿命以内且检测到结构存在损伤，经深入检测后可知，其损伤程度介于与之间，此时采用第1种维护措施。由此得到的桥梁最终使用寿命和检测维护成本按下式计算：

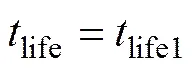
分支3：初步检测时间在结构初始使用寿命以内且检测到结构存在损伤，经深入检测后可知，其损伤程度大于，此时采用第2种维护措施，由此得到的桥梁最终使用寿命和检测维护成本按下式计算：

分支4：初步检测时间在结构初始使用寿命以内但没有检测到结构存在损伤，此时无需采取任何维护措施。由此得到的桥梁最终使用寿命和检测维护成本按下式计算：

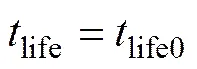
分支5：预定的初步检测时间已经超过结构的初始使用寿命，结构此时已经失效，因而也无需采取任何维护措施。由此得到的桥梁最终使用寿命和检测维护成本按式(25)计算。

4 桥梁检测维护策略多目标优化计算模型

对桥梁进行检测维护，有若干可供选择的检测方法和维护措施策略，则不同的检测维护策略将产生不同的桥梁预期使用寿命和检测维护总成本。对可供选择的检测维护策略进行优化即是通过选择适当的检测时间，优化的检测方法和维护策略决定准则，采用与当前损伤强度相对应的维护措施对结构进行维护，达到在检测维护成本最小的条件下延长结构使用寿命的目的。

对于钢筋锈蚀引起的混凝土桥梁使用性能退化，本文建立1个桥梁检测维护策略优化计算模型，即

目标函数：

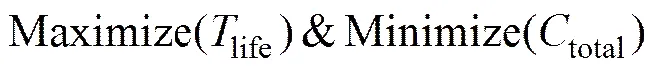
设计变量：

约束条件：

显然，式(26)是1个有约束的多目标多变量优化问题，目标函数为最大化桥梁使用寿命和最小化检测维护总成本；需要优化的设计变量为检测时间，检测方法优劣参数、维护策略决策准则限值和；约束条件包括相邻2次检测维护之间的时间间隔要大于1 a和根据经验限定的检测方法优劣参数、维护策略决策准则取值。采用MATLAB提供的遗传算法优化工具箱进行优化计算，即可得到该问题的Pareto优化解集。图5所示为基于Gamma过程的考虑钢筋锈蚀的钢筋混凝土桥梁检测维护策略优化计算流程图。

图5 基于Gamma过程的钢筋混凝土桥梁检测维护策略优化计算流程图

5 算例分析

以广西铁山港跨海大桥30 m跨主梁上部结构预应力钢筋混凝土空心板为例说明提出的检测维护策略优化计算模型的正确性。铁山港跨海大桥[18]位于广西铁山港中上段，位于滨海盐渍地区，属于强氯离子侵蚀。大桥全长2 898 m，共分为9联，其中50 m跨径1联、30 m跨径4联、20 m跨径4联。大桥30 m 跨主梁上部结构为宽幅预应力混凝土空心板，预制板为先张预应力混凝土结构，墩顶纵向湿接缝为后张法预应力混凝土结构。图6所示为铁山港跨海大桥30 m跨主梁中板跨中钢筋截面布置图。

单位：cm

表1所示为经过检测得到的铁山港大桥30 m跨底板钢筋锈蚀相关参数平均值。将表1中参数代入式(5)，计算得到钢筋锈蚀开始出现时间为30.33 a。

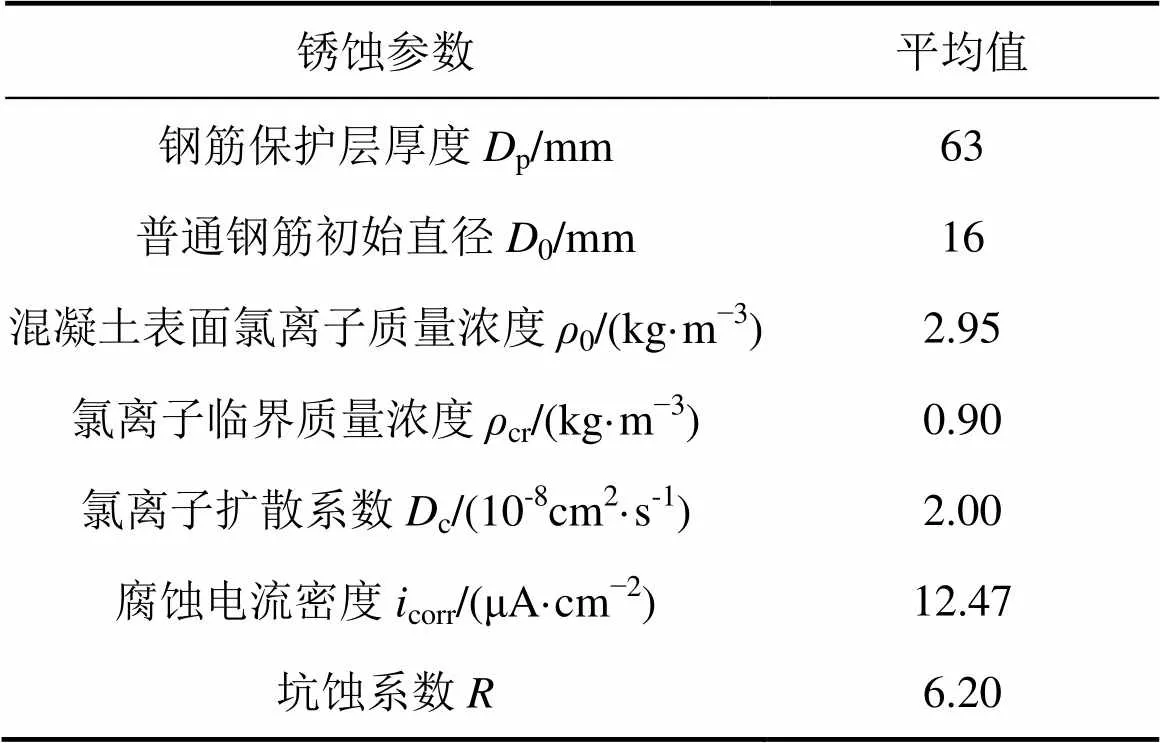
表1 铁山港大桥30m跨主梁底板钢筋锈蚀参数

假设钢筋局部锈蚀深度为形状参数为()，尺度参数为1的Gamma分布，当=14时，采用1.2节Gamma 桥采样方法模拟其发展过程如图7所示。不考虑钢筋局部锈蚀深度发展过程中的不确定性，当结构服役时间大于30.33 a时，钢筋局部锈蚀深度随使用时间呈线性增加；考虑钢筋局部锈蚀深度发展过程的不确定性，采用Gamma随机过程模拟其发展时，其增长过程是由一系列不同长度的微小增长段构成。

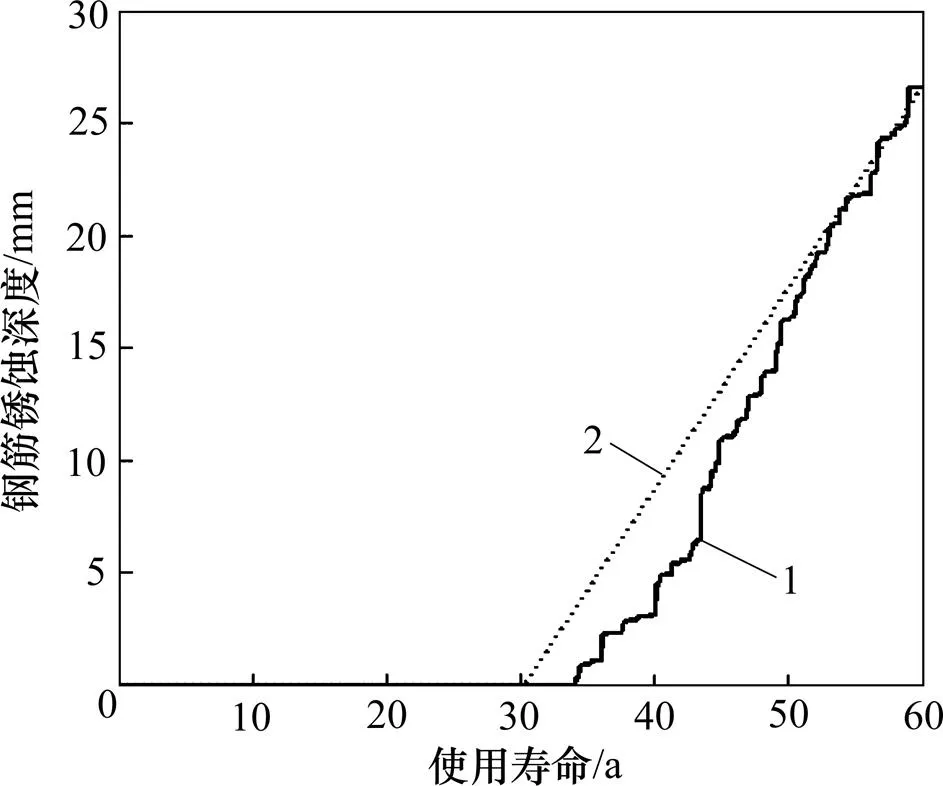
1—Gamma增长模型；2—线性增长模型

假设式(15)中钢筋平均锈蚀深度与钢筋初始直径比值life=0.006 5时，计算得到该桥钢筋最大局部锈蚀深度为max=6.448 mm。将其设定为阈值，由图8所示基于Gamma随机过程模拟得到的钢筋局部锈蚀深度发展曲线(局部图)，可以预测该桥考虑钢筋锈蚀的初始使用寿命为43.418 a。

图8 基于Gamma过程模拟的钢筋锈蚀深度发展曲线(局部图)

在桥梁结构的全寿命周期过程中，可进行多次检测和维护，其优化的检测维护策略确定较复杂。为了阐述桥梁检测维护策略的一般优化方法，本文仅考虑对桥梁结构进行1次和2次检测、维护2种情况，维护措施也仅考虑2种。其中，第1种维护措施的效果可将结构使用寿命延长8 a；第2种维护措施的效果可将结构使用寿命延长16 a。同时假定，对于单位桥梁维护，2种维护措施的成本为定值。表2所示为针对铁山港大桥30 m跨钢筋混凝土板梁进行钢筋锈蚀检测、维护的成本参数。

表2 铁山港大桥30 m跨主梁检测维护成本参数

根据多目标优化计算模型与表1和表2提供的铁山港大桥30 m跨主梁相关参数，分析检测维护决策树模型的不同分支计算目标函数life和total，以最大化结构使用寿命和最小化全寿命周期内检测维护成本为优化目标，以检测维护时间、检测手段、维护措施为设计变量，采用多目标遗传算法对该桥的检测维护策略进行优化计算，优化计算模型如下。

优化目标：

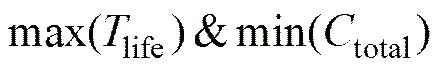
设计变量：

约束条件：

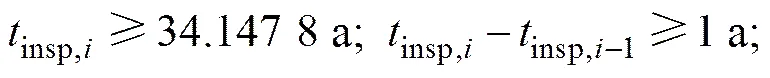
根据式(27)优化计算模型，分别考虑在桥梁全寿命周期内进行1次和2次检测维护，且维护措施在检测完成后立即进行。采用Matlab优化工具箱提供的遗传算法进行优化计算，得到检测维护策略的Pareto优化解集，如图9和图10所示。图中横坐标表示检测维护后的使用寿命，纵坐标表示达到该使用寿命所需付出的检测维护总成本，每个点代表1个优化的检测维护策略组合，包含检测时间、检测手段和决策依据等信息。

图9 检测次数为1时的检测维护策略Pareto解集

图10 检测次数为2时的检测维护策略Pareto解集

从图9和图10可以看出：随着桥梁使用寿命期望值的增加，总的检测维护成本也会相应增加。总检测维护成本增加意味着使用了检测效果较优的检测方法，采用了更有效的维护措施以及执行了更为严格的决策标准，以达到延长桥梁使用寿命的目的。

表3所示为图9和图10中A1，A2，B1和B2共4个检测维护策略优化解的取值，包括优化的检测时间、检测方法优劣参数、维护策略决策准则阈值以及预计的桥梁使用寿命和总检测维护成本。

表3 图9和图10中设计变量和目标函数计算结果

图9中检测维护策略A1(A2)表示桥梁在第38.9年(第40.1年)进行1次检测，采用的检测质量指标为0.14(0.17)的检测方法，相应的维护策略决策准则为[0.05,0.19]([0.05,0.15])。维护策略决策准则表示当检测得到的锈蚀损伤程度小于0.05(0.05)时，无需采取任何维护措施；介于0.05(0.05)到0.19(0.15)之间时采取第1种维护措施；若大于0.15(0.19)则采取第2种维护措施。在A1(A2)检测维护策略下，结构的最终使用寿命life=50.7 a(life=58 a)，检测维护总成本为289 521元(384 771元)。图11所示进一步给出了在A2检测维护策略下钢筋锈蚀深度的发展过程。

图10中检测维护策略B1(B2)表示桥梁在第37.2年和第46.0年(第37.3年和第48.2年)进行2次检测，2次检测采用的检测质量指标分别为0.12和0.16(0.07和0.14)的检测方法，相应的维护策略决策准则为[0.05,0.17]和[0.05,0.19]([0.04,0.15]和[0.04,0.18])。维护策略决策准则的含义类似。在B1(B2)检测维护策略下，结构的最终使用寿命life=50.7 a(life=67.4 a)，检测维护总成本为362 956元(519 042元)。图12所示进一步给出了在B2检测维护策略下钢筋锈蚀深度的发展过程。

从图11和图12可见：在实际工程应用中，业主或桥梁等基础设施管理部门可根据拥有的资金和对结构的预期使用寿命，从检测维护策略Pareto优化解集中选择能同时满足其使用性和经济性要求的优化检测维护策略。

1—检测维护前锈蚀深度发展过程；

1—检测维护前锈蚀深度发展过程；2—2次检测维护后锈蚀深度发展过程；

6 结论

1) 针对考虑钢筋锈蚀的钢筋混凝土桥梁结构，可将基于钢筋局部锈蚀深度的结构损伤强度指标作为表征结构使用性能的退化指标，Gamma过程可模拟钢筋局部锈蚀深度发展过程的不确定性。

2) 提出了考虑钢筋锈蚀检测概率和维护措施影响的结构使用寿命预测模型和基于决策维护树模型的检测维护成本计算模型；以最大化桥梁经检测维护后的使用寿命期望和最小化检测维护成本为优化目标函数，提出了基于Gamma过程和遗传算法的锈蚀钢筋混凝土桥梁结构检测维护策略优化分析方法。

3) 算例分析1座钢筋混凝土桥30 m跨主梁，得到了包含检测维护时间、检测手段和维护决策准则等内容的优化检测维护策略Pareto解集。结果表明：得到的Pareto优化解集可以提供在不同结构使用寿命期望和检测维护成本预算下收益最大的检测维护策略。

[1] Frangopol D M. Life-cycle performance, management, and optimization of structural systems under uncertainty: accomplishments and challenges[J]. Structure and Infrastructure Engineering, 2011, 7(6): 389−413.

[2] Jandu A S. Inspection and maintenance of highway structures in England[J]. Proceeding of ICE, Bridge Engineering, 2008, 161(3): 111−114.

[3] Ellingwood B R, Mori Y. Reliability-based service life assessment of concrete structures in nuclear power plants: Optimum inspection and repair[J]. Nuclear Engineering Design, 1997, 175(3): 247−258.

[4] Enright M P, Frangopol D M. Maintenance planning for deteriorating concrete bridges[J]. Journal of Structural Engineering, ASCE, 1999, 125(12): 1407−1414.

[5] Stewart M G. Spatial variability of damage and expected maintenance costs for deteriorating RC structures[J]. Structure and Infrastructure Engineering, 2006, 2(2): 79−90.

[6] van Noortwijk J M. A survey of the application of Gamma process in maintenance[J]. Reliability Engineering & System Safety, 2009, 94(1): 2−21.

[7] 秦权. 基于时变可靠度的桥梁检测与维修方案优化[J]. 公路, 2002(9): 17−25. QIN Quan. Optimal bridges inspection and repair strategy based on time-dependent reliability[J]. Highways, 2002(9): 17−25.

[8] 杨伟军, 张建仁, 梁兴文. 基于动态可靠度的服役桥梁维修加固策略[J]. 中国公路学报, 2002, 15(3): 49−52. YANG Weijun, ZHANG Jianren, LIANG Xingwen. Strategy of repair and reinforcement on existing bridges based on time-dependent reliability[J]. China Journal of Highway and Transport, 2002, 15(3): 49−52.

[9] 邵旭东, 彭建新, 晏班夫. 基于结构可靠度的桥梁维护策略优化研究[J]. 工程力学, 2008, 25(9): 149−155, 197. SHAO Xudong, PENG Jianxin, YAN Banfu. Structural reliability-based life-cycle cost optimization of maintenance interventions for deteriorating bridges[J]. Engineering Mechanics, 2008, 25(9): 149−155, 197.

[10] Kim S, Frangopol D M. Generalized probabilistic framework for optimum inspection and maintenance planning[J]. Journal of Structural Engineering, ASCE, 2013, 139(3): 435−447.

[11] 周浩, 黄天立, 任伟新, 等. 基于概率的锈蚀钢筋混凝土桥梁检测维护策略优化研究[J]. 中南大学学报(自然科学版), 2014, 45(12): 4292−4299. ZHOU Hao, HUANG Tianli, REN Weixin, et al. Probabilistic optimum inspection and maintenance strategy for reinforced concrete bridges due to reinforcement corrosion[J]. Journal of Central South University (Science and Technology), 2014, 45(12): 4292−4299.

[12] 金伟良, 袁迎曙, 卫军, 等. 氯盐环境下混凝土结构耐久性理论与设计方法[M]. 北京: 科学出版社, 2011: 209−218. JIN Weiliang, YUAN Yingshu, WEI Jun, et al. The theory and design method of durability of concrete structure in chloride environment[M]. Beijing: Science Press, 2011: 209−218.

[13] Stewart M G. Spatial variability of pitting corrosion and its influence of structural fragility and reliability of RC beams in flexure[J]. Structural Safety, 2004, 26(4): 453−470.

[14] Val D V, Melchers R E. Reliability of deteriorating RC slab bridges[J]. Journal of Structure Engineering, 1997, 123(12): 1638−1644.

[15] Avramidis A N, L’Ecuyer P, Tremblay P A. Efficient simulation of gamma and variance-gamma processes[C]// Chick S, Sa´nzhes P J, Ferrin D, et al. Proceedings of the 2003 winter simulation conference. Piscataway. NJ: Institute of Electrical and Electronics Engineers (IEEE), 2003: 319−326.

[16] Crawshaw J, Chambers J. A concise course in A-level statistics[M]. Stanley Thornes Publishers, Cheltenham, UK, 1984: 30−50.

[17] Torres-Acosta A A, Martinez-Madrid M. Residual life of corroding reinforced concrete structures in marine environment[J]. Journal of Materials in Civil Engineering, 2003, 15(4): 344−353.

[18] 朱绩超. 氯离子环境下钢筋混凝土桥梁耐久性研究[D]. 长沙: 湖南大学土木工程学院, 2008: 46−60. ZHU Jichao. Durability study of reinforcement concrete bridge under chloride ion environment[D]. Changsha: Hunan University. School of Civil Engineering, 2008: 46−60.

Optimization inspection and maintenance strategy for corrosive reinforced concrete girder bridges based on Gamma process

HUANG Tianli1, ZHOU Hao1, WANG Chao2, REN Weixin1, CHEN Huapeng3

(1. School of Civil Engineering, Central South University, Changsha 410075, China; 2. School of Civil Engineering & Architecture, Hubei University of Technology, Wuhan 430068, China;3. Department of Civil Engineering, University of Greenwich, Chatham Maritime, Kent, ME4 4TB, London, UK)

For the deterioration of reinforced concrete (RC) girder bridges due to reinforcement corrosion, the corrosion depth of reinforcement was used to characterize the performance deterioration of structure and the Gamma process(GP), and the uncertainties involved in the service of bridges were considered in simulating the propagation of corrosion depth. Considering the probability of detection (PoD) of reinforcement corrosion and maintenance, the service life prediction model was proposed. The inspection and maintenance cost model was also proposed based on the inspection and maintenance decision tree model. Based on maximization of the expected service life after inspection and maintenance and minimization of the expected inspection and maintenance cost, a method using the GP model and genetic algorithm (GA) to optimize the inspection and maintenance strategy was proposed to reduce the reinforcement corrosion of RC girder bridges. A 30 m span RC girder of the Guangxi Tieshan Port Bridge was calculated to get the Pareto solutions set of inspection and maintenance strategy. The results show that the Pareto solutions can provide the most profitable strategy under different service life expectations and economic budgets as well as decision reference for owners or civil infrastructure administrators in choosing inspection and maintenance strategy.

reinforced concrete girder bridge; reinforcement corrosion; optimization inspection and maintenance strategy; Gamma process; genetic algorithm

10.11817/j.issn.1672-7207.2015.05.038

P315.96；TU311.3

A

1672−7207(2015)05−1851−11

2014−08−12；

2014−10−15

国家自然科学基金资助项目(51478472，51408250)；湖南省自然科学基金资助项目(2015JJ2176)；英国皇家工程院牛顿基金资助项目(Reference NRCP/1415/14) (Projects(51478472, 51408250) supported by the National Natural Science Foundation of China; Project(2015JJ2176) supported by the Natural Science Foundation of Hunan Province, China; Project(Reference NRCP/1415/14) supported by the Royal Academy of Engineering-Newton Fund, UK)

黄天立，博士后，副教授，从事桥梁结构健康监测及检测维护策略优化研究；E-mail: htianli@csu.edu.cn

(编辑 陈灿华)