基于过程教学视域下的初中“勾股定理”教学探究

姚军

[摘 要] 新课标改革下对数学教学的要求是“以学生发展为本”，因此在数学教学过程中，我们不仅要教会学生数学知识，更要培养学生的思维能力，而过程教学则以其独有的教学过程被引入新课标下的数学教学过程中，我们将从初中勾股定理的教学任务出发，研究基于过程教学视角下数学教学的主要方法，并结合实际案例，开展勾股定理教学的整个过程.

[关键词] 过程教学；初中数学；勾股定理

过程教学法最开始的发展是针对写作过程，过程教学法认为写作的过程是一种群体间的交际活动，而不是作者的单独行动，因此过程教学法通过充分培养学生的思维能力来提高学生的写作能力，从而将教学重点放在学生的写作过程上. 在新课标对教学改革工作的不断需求下，我们将过程教学引入到数学教学过程中是非常可行的. 过程教学法更加尊重被教育者的知识结构和认知水平，切合教学目的和任务，创造合适的问题场景，通过教学过程分析和解决问题，从而达到最终的教学目的，这是过程教学法的核心思想.

过程教学的内涵

过程教学法的核心在于教学过程，无论是教师的授课过程，还是学生的学习过程，过程教学都要求学生能在过程中思考，并在思考的过程中加深对所学知识的理解. 过程教学法具体表现在以下几方面.

（1）充分认识教学过程中“知识”的生成过程. 什么是知识生成过程，拿我们要说的勾股定理来说，勾股定理的应用能够追溯到公元前约3000年的古巴比伦，并且他们已经知道了很多勾股数组（3，4，5即为一个勾股数组）. 在中国公元前十一世纪的时候，周朝就有了“勾三股四弦五”的记载，勾股定理的发展历史只是勾股定理知识产生过程中的其中一环. 对于过程教学，我们更加要理解知识的发生以及应用发展的整个过程——从定理的猜想到假设，再到定理的证明等阶段，深刻认识到数学知识生成的逻辑顺序.

（2）教学过程更加是思维发展的过程，即在教学过程中不断发展和完善学生的思维能力，因此，过程教学也要再现人类研究问题的特征，即知识从失败到成功的过程. 教学过程更加要结合学生思维的特点，引导学生主动地思考. 学生走入误区不是坏事，这是人类思考问题的共性，符合人类思维过程的特点. 过程教学不是一种怎样的教学手段，更为体贴的描述应该围绕教学目标，让学生思考整个过程的指导，忽视结果，重视过程，重视对知识的探索过程.

定理教学的特点

就数学教学过程中的定理教学而言，难的不是在于定理的证明过程，而是在没有定理出现的时候，面对问题的发生和解决，人类是怎样思考并找出这个定理的，因此对于定理教学，就更加需要过程教学的辅助，结合过程教学的主要思想，让学生清晰地认识定理的发现、探索，以及最后获取的过程，培养学生自主思考的能力. 通过过程教学开展定理教学的主要方式有：

（1）数学定理的导入环节当作过程教学的开始，其主要目的在于解释知识背景，这个过程中需要教师拿出具体的生活案例激发学生探究和学习新知识的渴望. 例如，现在有一个直角三角形，我们知道了两条直角边的长度，根据三角形的特点，第三条边能否通过计算得出来？下面我们开始教学活动.

（2）定理的重构环节是教学难点. 由于大家对这个定理已经非常熟悉，当然这都是很多科学家总结出来的，重构勾股定理发展的过程实际上具备一定的难度，这就需要教师根据学生现有的知识结构，模拟并且重构勾股定理的发展过程，并且在过程中学生主动思考和探索.

（3）定理的运用环节. 运用也是过程教学中不可缺少的重要环节，能检验学生对定理的掌握程度. 过程教学虽然更加注重过程，但如果学生不能学到知识，不能运用新知识去解决问题，那么整个教学过程就是失败的. 定理运用的环节能够强化学生对勾股定理的理解.

过程教学视域下的教学案例

通过上文我们知道了过程教学在定理教学中的运用方式和注意事项，那么，如何根据实际开展勾股定理的教学工作呢？具体的教学过程安排如下：

1. 定理的导入环节

其中一种方式是从数学史的角度，即我们可以通过展示中国邮政发布的一枚标有中国古代证明勾股定理的赵爽图来开展定理的导入环节；也可以这样进入引入环节：拿一根长1.2米的白绳子，通过测量30，40，50厘米长的绳子组成一个三角形，让部分同学在黑板上测量角度.

2. 定理的重建过程

我们都知道，勾股定理的具体内容是在直角三角形中两条直角边的平方和等于斜边的平方，具体的表述为：

c2=a2+b2 （a，b分别为直角边，c为斜边）

定理针对所有的直角三角形，那么这个定理的建立过程一定是从特殊到普遍，因此在勾股定理的重构过程中，我们可以通过演示特殊的直角三角形开始展开勾股定理的重建.

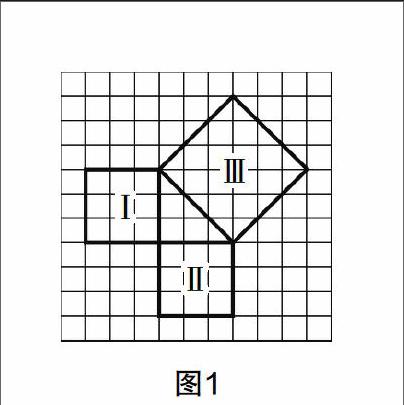
例如，在一个格点图形中（如图1），每个小方格都是均等的，而且假设小方格的边长都是1，即面积也是1，于是可任意找一个定点都在格点的直角三角形，然后分别以这个三角形的每一条边作正方形，然后计算斜边作为边长的正方形的面积.

通过割补等不同的方法，能让学生自己探索正方形Ⅲ的面积. 既然在单位是1的格点图形中，直角边和斜边满足一定的数量关系，那么是不是其他比例下也同样满足呢？如果单位是1.1呢？具体的实现过程是不是也满足呢？可根据等式两边同时乘1.1，等式依然成立，来引出定理的一般性.

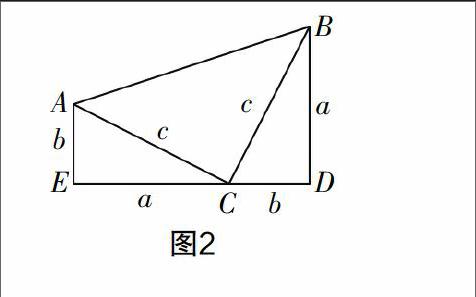
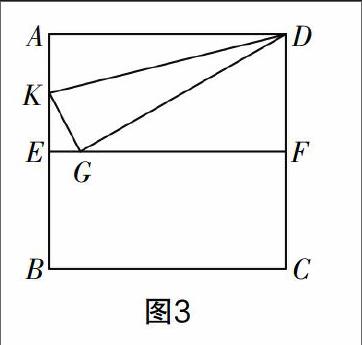
或者，我们可以通过在课堂上演示加菲尔德证法的实现过程来完成定理的重构. 比较有趣的是，加菲尔德在证明这个结论以后的几年，成为美国总统，因此又叫总统定理，这样的趣味性也能够增强过程教学中学生的注意力. 加菲尔德证法也是通过面积求和的思想实现的，如图2所示.

教师一定要积极引导，但不能直接提醒面积求和的思想，应让学生在对定理的探索过程中，主动发现和思考，教师还应创造一定的情景，引出面积总和的思想. 总之，学生对定理的探索过程非常重要，能加深其对勾股定理的理解，而且对于以后勾股定理的实际运用有非常大的帮助.endprint