立足学生视角，实现教与学的有效对接

叶亮亮

[摘 要] 古希腊大教育家苏格拉底认为，教育首先需要的，是教师退回到学生的角色，而后展开相机诱导，使学生展开自主探究，获得思维能力的发展. 本文提出，要立足学生视角，将教师身份向学生身份转换，用学生的思维和眼光审视所学内容，实现教与学的有效对接.

[关键词] 学生视角；小学数学；课堂教学；策略引导

新课改以来，各种教学流派和教学模式如雨后春笋，催生出课堂教学“泛技术主义”的误区，教师热衷于目标的设定和教学环节的预设，热衷于各种多媒体技术的应用，但在这众多热闹的教学实验背后，却隐藏着一个致命的问题，那就是教师的强势侵入——看似是为了学生，但实际上却是信息轰炸，让学生眼花缭乱，感到迷茫，感到被代替，感到被操纵. 这样的教学后果显然与课改的初衷相背离.

为什么我们的课堂热闹了，却离学生更远了？究其原因，主要在于教师给予学生的不是走路的方法，而是一条已经预设好的路，这剥夺了学生进行个性思考的权力，也剥夺了学生进行自我体验的必要过程，导致学生思维的僵化. 如何突破这一困境，实现新课标提出的“发挥学生主体作用，培养学生的个性化发展”呢？笔者认为，教师要做的就是立足学生的视角，退回到学生的身份和思维中，将思维“儿童化、幼稚化”，由此实现教与学的有效对接. 现根据笔者的教学实践，谈一谈对这一问题的思考和体会.

突破固有经验，读懂学生的学情

在小学数学教学中，教师通常会囿于教学惯性，根据自己的固有教学经验，从自己的思维模式出发，预设一些教学环节，让学生走进轨道中，使其不能出于其外. 这种做法显然不利于学生主体作用的发挥. 基于此，教师应突破固有模式，“蹲下去”读懂学生，关注学生之间的个体差异，关注不同的学情，从这里找到突破口. 那么，如何读懂学生呢？笔者认为，教师可以从两个方面入手.

1. 寻找学习认知的冲突点

由于学生个体存在差异性，每个人的认知也存在差异，因此，教师要从这个差异性出发，找到学生学习的冲突点. 例如，教学“圆的认识”一课时，经过课前调查，笔者发现90%的学生都能画出圆，却对圆的作用所知甚少. 为此，在课堂探究时，笔者将圆的性质和作用当作重点，带领学生展开操作与实践，进行自主学习. 这样的教学设计有明确的目标和方向，有效避免了看似热闹的“假探究”，提高了学生的自主学习能力.

2. 寻找已知和未知的矛盾点

例如，教学“两位数乘两位数”时，学生一开始很快就掌握了计算法则，但到实际应用时立刻原形毕露，一筹莫展. 为避免这种情况的发生，笔者学习前进行了前测：你如何计算12×34？有70%的学生能够采用累加的方法来进行计算，有10%的学生提出可以采用竖式计算，有3%的学生提出可以将其转换为乘数为一位数的乘法. 为此，笔者根据学生已知和未知之间的矛盾点，设计了两个层次的教学，让学生从累加的方式逐步过渡到乘数为一位数的乘法，再过渡到竖式，这样有的放矢的教学，逐层递进，能让学生在理解算理的基础上掌握算法，大大提升学生的数学能力.

展开智慧引导，提升学生思维

对于学生来说，教师是文化天使，能够引领每一个儿童进入智慧的殿堂. 在小学数学教学中，教师在课堂中所担当的角色是引导者，而不是主宰者. 因此，教师要通过智慧的引导，追寻适合学生的教学方法，这样才能帮助学生获得思维的有效提升. 这里需要做到以下两个方面.

1. 在困惑处释疑

学贵有思，思贵有疑. 在学生困惑的地方进行引导，有利于学生思维的生长. 例如，教学“认识钟表”这一内容时，在进行学前测试环节，笔者出示了图1所示的钟表，有学生认为这是3：12，也有学生认为这是3：00，到底哪种是正确的呢？一部分学生认为，3：00是正确的；一部分学生认为时针指向3，分针指向12，但不知道错在哪里. 基于此，笔者站在学生的视角发现，这个错误的根本在于，钟面是一个封闭的系统，1～12围成的圈让学生找不到哪里是起点“0”，为此，笔者调整钟表的多个时刻，引导学生思考：为什么分针都指向12？学生由此发现12的意义：既是上一个整时的结束，又是下一个整时的开始，有效地解答了教学疑问.

2. 在难点处点拨

在小学数学教学中，学生学习的难点大多是思维容易出现误区的地方，也是思维提升的关键点. 教师要紧抓难点，尝试采用多种教学方式进行引导，拨乱反正，点拨学生的思维，使其获得突破. 例如，学完面积和周长之后，学生常常会混淆这两个概念，主要是因为学生从线到面的空间能力发展需要一个过渡和飞跃的过程. 根据认知心理学，相比线来说，面是一个弱刺激源，因而学习面积时就会受到周长的影响，导致面积概念出现误区. 根据这一学情，笔者在教学中加强了对比引导：先用摸一摸的方法，感受周长和面积的区别；再用画一画的方式，建立面积和周长的清晰表象；最后用算一算的方法，计算面积和周长，建构面积和周长的概念. 由此，学生发现，周长和面积是完全不一样的两个概念，一个是线构成的，一个是面构成的，两者的意义、计算方法、画法也截然不同.

善待错误资源，发展数学能力

著名教育人郭思乐老师曾经指出：“教学并不是教给学生3乘5等于15，而是要敢于教给学生3乘4等于15.”这句话听起来很奇怪，但实际上这是教育的真谛，因为这是要教给学生探究“为什么错”，从而找到“如何才能对”的路径，探究“为什么是这样而不是那样”的原因，从而获得对数学本质的理解. 但在传统教学模式中，教师往往致力于教给学生“不能犯错”“不敢犯错”，教师也为学生的错误头疼不已. 笔者认为，教师要敢于将学生的错误当作有效的资源，从积累这些资源入手，教给学生从“不对”到“对”的数学思维，发展学生的数学能力.

1. 营造纠错环境

学生出现错误是难免的，教师要客观、公正地看待这一问题，并积极营造纠错环境，增强学生的思维反思能力，从错误中发现错误所在，找到原因并进行解决. 如解答这样一道习题：一块长方形铁皮的长为16厘米，宽为8厘米，如果要剪一个直径为2厘米的圆片，最多可以剪多少个？学生列式计算：16×8÷[3.14×（2÷2）2]，结果约等于40片. 此时笔者站在学生的角度引导：为什么要这样计算？怎么想的？学生指出，先求出长方形铁皮的面积，然后求出直径为2厘米的圆片的面积，看大的面积中有几个这样的圆形面积，因而要用除法. 此时，我并没有直接指出错误，而是让学生进行分析：现在画图看看，到底如何剪？你发现了什么？学生由此发现了自己的错误所在，并得到正确的认知. 教师通过这样的引导，为学生营造了一个和谐的纠错环境，有利于下一步对错误的改进.

2. 强化纠错分析

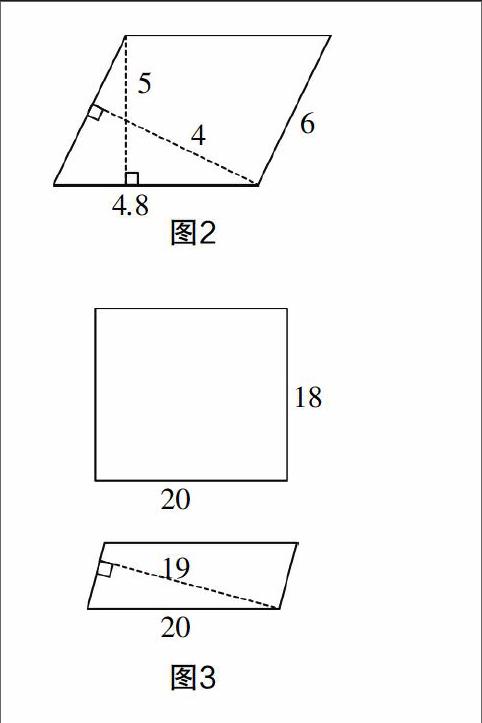
教师在教学时一定要加强纠错分析，帮助学生衔接所学知识的链接点，让学生进行深度探究. 例如，有这样一道题：平行四边形的两条邻边分别为4.8厘米、6厘米，两条高分别为5厘米、4厘米（如图2），求这个平行四边形的面积. 有学生列式计算为4.8×4，也有学生列式为6×5，结果两种计算结果完全不一样. 到底哪种才是错误的呢？笔者展开引导：如图3所示，你认为平行四边形的面积可以用20×19（底边乘另外一条边上的高）来进行计算吗？为什么？学生发现，不能这样计算，因为这样计算之后，图3中长方形的面积小于这个平行四边形的面积，显然这是错误的. 因此，平行四边形的面积计算必须是底边与对应的高相乘，由此，学生克服了自己的思维错误，深刻理解了平行四边形面积计算的本质.

总之，在小学数学教学中，教师的教和学生的学是一对有机体，不能以教师的教扭曲学生的学，而要师生的心都往一个地方努力，教师要站在学生的视角，从学生的角度入手，这样才能让数学课堂变得人性化，最大限度地发挥学生的主观能动性，使数学课堂成为学生的课堂，实现教与学的有效对接，为学生的思维发展提供动力.cendprint