全耦合S型铺管动力定位时域分析
孙丽萍,朱建勋,艾尚茂,刘胜楠
(哈尔滨工程大学深海工程技术研究中心,黑龙江哈尔滨 150001)
目前,在深水和离岸相对远的海域,海底管道的铺设一般要使用铺管船,铺管形式包括了S型、J型以及卷筒法等。其中应用最为广泛的是S型铺管法。随着作业水深的不断推进,动力定位在铺管船上的使用已经越发广泛。近几十年来,动力定位系统在国内外已经有了非常长足的发展。Chen等[1]研究了离岸钻井装置的动力定位系统,通过三个限制条件函数,防止定位失效、船体移动以及钻井口完整性的破坏。Holvik和Morgan[2-3]研究阐述了动力定位系统在深海半潜式平台的应用。Tannnuri[4]研究了动力定位系统作用下穿梭油轮的卸载工况响应。王磊等[5-7]对半潜浮式结构上的动力定位系统性能以及锚泊辅助动力定位领域进行了比较深入地研究。徐海祥等[8-9]对动力定位系统的外载荷计算模拟进行了较为完善的研究。孙丽萍等[10]采用数值模拟与实验验证相结合的方法,分析了半潜式平台推进器失效后的平台定位能力。宋林峰等[11]采用了简易的PID动力定位系统,对S型铺管船的铺管工况进行了耦合运动分析。
采用应用广泛的PID以及Kalman滤波相结合的动力定位系统,采用序列二次规划法[12]进行推力分配,对铺管工况下的S型铺管船耦合运动进行动力定位时域模拟,对铺管作业提供参考。
1 数值计算方法
1.1 船体运动方程
对于动力定位系统而言,一般只考虑船体水平三自由度(纵荡、横荡以及垂荡)的运动。但是对于铺管工况下的铺管船运动,波频运动中的垂荡和纵摇会对管道作用力有一定影响。因此,采用三维辐射绕射理论,得到了水动力系数附加质量矩阵Ma,以及阻尼矩阵A。将船体频域计算的水动力系数代入时域耦合方程[13]:

式中:Fenv表示船体所受的环境载荷,包括风、浪、流载荷;Fpipe表示管道和托管架对船体的作用力;FDP为动力定位系统的推力作用。
1.2 动力定位系统
动力定位系统,主要对船舶的纵荡、横荡以及艏摇三个自由度上的运动实施控制。目前应用最广泛和成熟的是采用PID控制与Kalman滤波结合的第二代动力定位系统。
1)PID控制方程
引入风前馈后的PID控制方程:

式中:ε为测量值与基准值之差;Kp,KI,KD分别为比例增益系数、积分增益系数和微分增益系数;FW为风的反抗力或力矩。
2)Kalman滤波器
在设计动力定位系统过程中,滤除各传感器测到的信号中的干扰和噪声,如船舶运动信息(低频信号和高频干扰信号)、未建模噪声等等,显得十分重要。
Kalman滤波器[14]通过新测数据和前一时刻的状态值X^k(),结合系统状态方程,按照如下递推公式,得到新的状态估计值X^k+1( )。状态预测器:

协方差预测器:

Kalman滤波增益:
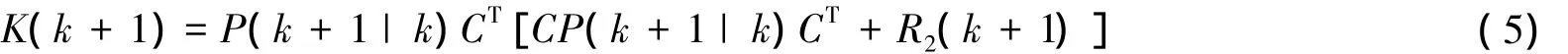
状态修正器:
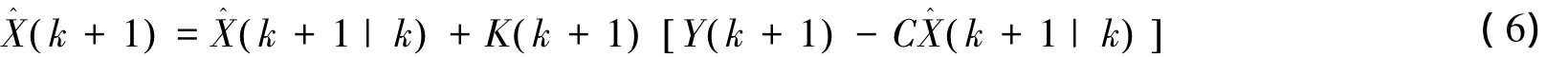
协方差修正器:
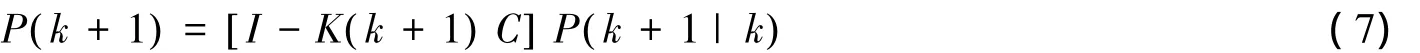
式中:U(k)为当前控制输入和环境载荷,C为正定矩阵,R1和R2为噪声信号方差。
3)推力分配
推力分配本质是一个非线性约束最优化的求解过程。采用序列二次规划法,通过每步迭代由一个二次规划子问题来寻找下一个下降方向,从而减少度量函数取得步长,重复迭代得到最优解。
从经济角度考虑,采用功耗最小作为目标函数,如下式所得:

约束条件分为三个:三个水平自由度的推力信号等式约束;禁止角和最大推力的不等式约束。

式中:x2i,x2i-1分别为x方向和y方向的推力;α,αu,αl分别为推力角度、禁止角上限、禁止角下限。
1.3 托管架和管道耦合模型
铺管船在铺设管道过程中,管线和托管架对船体的作用,将直接影响动力定位的精度以及其功率的消耗。因此,管道的受力情况对于动力定位系统而言是不可忽略的一项。
管道可分为托管架上的上弯段、中垂段,以及接近水面的下弯段。
对于管道,采用了质量集中法,将管道离散成一系列的点。这些点由无质量的弹簧单元连接来模拟管道的受力和运动,离散后的管单元质量集中在各离散点上。在管单元之间采用轴向弹簧、扭转弹簧和阻尼器来模拟管道的轴向和扭转特性。此外,在离散点的两端,使用转动弹簧和阻尼器来模拟管道的弯曲特性。采用非线性轴向刚度的管道,其有效张力计算如下:
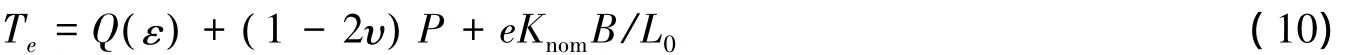
式中:Q(ε)为管壁张力与应变关系函数,υ为材料泊松比,ΔP为管道内外压力差,Ai和A0分别为管道内外截面积,e为管单元的伸长速率,Knom为管道零应变轴向刚度,B为轴向阻尼系数,L0为管道单元初始长度。
采用线性、同向的弯曲刚度,弯矩M通过扭转弹簧和阻尼器上的模拟计算得到:

式中:EI为弯曲刚度,Z为曲率,w(Z)为曲率变化率,γb为目标弯曲阻尼,Dcrit为临界刚度。
托管架对于管道的作用,主要是托管架上托辊的支撑作用。从而使管线上弯段呈现出上拱的形状。此外,管道顶端受到张紧器的张拉作用,管道与托管架之间采用U型支撑,底部支撑用于支持管道重力,两侧约束管道的横向位移。托辊的支撑仅模拟为单向支撑,当支撑与管道的相对位移产生压缩后起作用。其支撑刚度计算如下[15]:

式中:Wp为两个支撑点的距离;D为管道外径。
1.4 起重铺管船动态模拟流程
起重铺管船动力定位的模拟流程如图1所示。
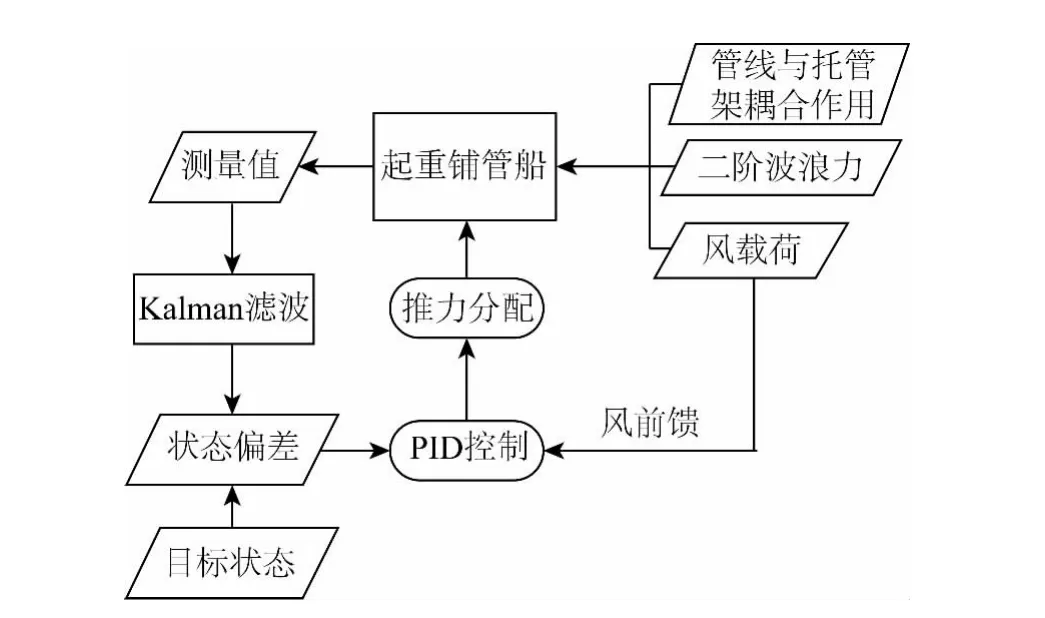
图1 动力定位模拟流程Fig.1 Simulation process of dynamic positioning
2 计算模型
2.1 船体及推进器主要参数
表1给出了起重铺管船的主要参数。

表1 船体主要参数Tab.1 Parameters of the hull
深水起重铺管船的水动力模型如图2所示,船体的面元总数3 459个,相对雅阁比系数均在1到2之间,托管架几何模型采用莫里森方程计算,然后对整个模型进行频域计算,得到附加质量系数、阻尼系数、六自由度运动响应函数等。
铺管船的推力系统由7个全回转推进器组成,如图3所示,推进器主要参数如表2所示。

图2 铺管船和托管架的组合模型Fig.2 Model of S-lay barge with stinger

图3 推进器布置Fig.3 The arrangement of thrusters

表2 推进器主要参数Tab.2 Parameters of the thruster
2.2 环境载荷
对于铺管船,上层建筑较为复杂,目前尚无规范性的风力系数曲线进行取值。根据API规范,采用模块法对有效投影面积进行计算,从而得到相应的风力系数。

式中:i,j表示上层建筑各构件;A,B分别表示构件沿风向的投影面积;Ch,Cs分别为风力高度系数和形状系数;α表示风向;Cw即为风力系数。
由于铺管船的水下部分船体近似于OCIMF[16]选取的船型,流载荷根据OCIMF取得流力系数CD。风、流载荷计算如下:

式中:Vz为海平面上10 m处的平均风速;在计算风、流载荷纵向力时,S为纵荡面积;计算风、流横向力时,S为横荡面积;计算风、流弯矩时,S为艏摇面积矩。
动力定位主要考虑波浪力中二阶慢漂力的影响,根据Pinkester[17]的近场理论,先利用三维物源法基于物面的压力和力矩积分,在频域中计算出在任一给定波浪遭遇角的二阶传递函数,再应用Fourier变换把二阶传递函数QTF转化为二次脉冲响应函数gi(τ1,τ2)。然后再结合波浪时历ζ(t),可得二阶漫漂力计算式:

环境载荷方向,如图4所示。
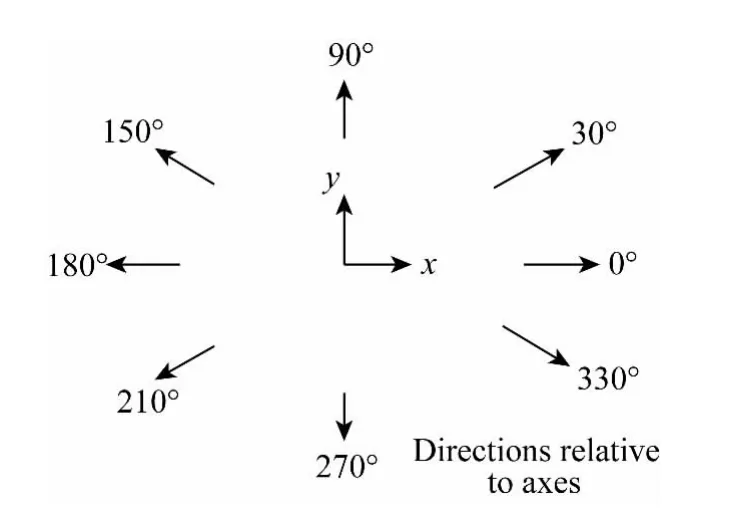
图4 环境载荷方向Fig.4 The environment load directions
3 结果与分析
使用水动力软件Ocaflex建立管线、托管架和船体的耦合模型,利用动态链接数据库(DLL)实现对动力定位系统的模块调用。采用C++编译工具把动力定位系统编译封装到动态链接数据库中,应用Ocaflex的外部函数调用功能,选择路径调用动力定位系统模块,实现动力定位与水动力模型的结合。
起重铺管船的铺设水深为1 175 m,管道直径为0.61 m,壁厚为0.062 m,总长为2 243 m,托管架的曲率半径为110 m。采用Jonswap波浪谱,有义波高为2.5 m,周期为6.22 s;用NPD风谱来模拟风载荷,平均风速取 16 m/s;流速取为 1.47 m/s。文中设计了 0°、45°、90°、135°和 180°的环境载荷,假设风浪流同向。
3.1 波频运动影响分析
通常做动力定位系统性能分析时,只考虑3个水平自由度,不考虑船体的另外三个自由度的运动。因为铺管船的波频运动对管道轴向张力的影响主要体现在垂荡、纵荡和纵摇上。纵荡被动力定位所控制,影响较小。因此只考虑垂荡和纵摇情况下,对管道水平作用力变化的影响。
选取了环境载荷为0°时,铺管船的垂荡、纵摇的时历曲线,如图5所示。图6给出了管道对铺管船的水平作用力。在考虑波频运动,与不考虑波频运动状态下,比较分析管道对船体的水平作用力。不考虑波频运动,即传统的动力定位模拟方式,只考虑水平三自由度的运动;考虑波频运动,即考虑船体在垂荡和纵荡方向上的运动。
从图5可见船体在垂荡和纵摇方向上的变化。如图6所示,选取150 s后的管道作用力为统计数值。无波频运动状态下,管道对船体的作用力平均值为-1 215.215 kN,最大值为-1 194.019 kN,最小值为-1 246.257 kN,方差为 8.19;含波频运动状态下,管道的水平作用力平均值为-1 209.65,最大值为-896.657 kN,最小值为-1 561.555 kN,方差为103.79。可见,管道-托管架-船体之间的耦合作用下,铺管船的波频运动对管道轴向拉力的变化影响非常大,在铺管船动力定位时域模拟中,不能忽略波频运动的影响。

图5 在环境载荷0°时,铺管船的垂荡、艏摇的时历曲线Fig.5 The heave and yaw of the ship within 0°environmental load
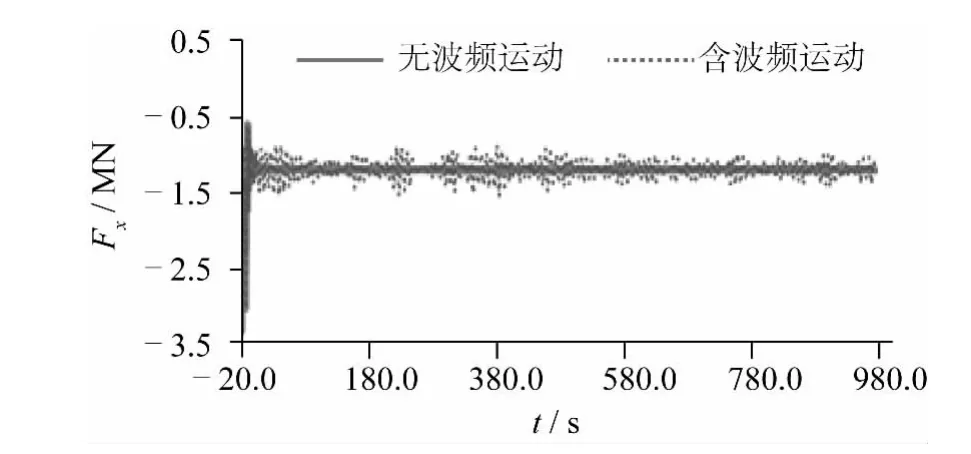
图6 管道对船体x方向的作用力Fig.6 Pipe force in x direction
针对动力定位系统控制范围只在水平三自由度,这里还进行了两种对比:只含垂荡运动,该水平作用力平均值为-1 214.95 kN,最大值为-1 168.43 kN,最小值为-1 260.92 kN,均方差为14.62;只考虑船体的纵摇运动,该水平作用力平均值为-1 211.33 kN,最大值为-952.28 kN,最小值为-1 518.22 kN,均方差为88.74。由于船体垂荡只引起了管道垂向位置的变化,而纵摇不仅引起了垂向变化而且轴向拉力角度变化也很大,导致管道自身重力和拖拽力的轴向拉力分量变化较大。因此,管道水平作用力的变化,约85%由纵摇引起,15%由垂荡引起。在管道铺设中,纵摇将很大程度地影响动力定位系统的消耗,施工时应注意这一点。
3.2 铺管船动力定位时域模拟
3.2.1 管道与托管架的耦合作用对动力定位系统定位精度的影响
为了分析管道耦合作用对动力定位系统定位精度的影响,选取了135°环境载荷,非铺管工况和铺管工况的时域模拟,模拟时间为4 000 s,动力定位的目标位置为x=92 m,y=0 m,yaw=0°。
图7为铺管船水平运动时历曲线。表3给出了数据统计,由于非铺管工况下,船体艏摇在2 000 s左右趋于稳定,故选取2 000 s至4 000 s的数据进行统计。

图7 铺管船水平运动时历Fig.7 Horizontal motion of S-lay barge
由表3可知:铺管工况下,船体纵荡约为-4.333 m,横荡约为0.584 m,艏摇约为-3.911°;非铺管工况下,船体纵荡约为-0.748 m,横荡约为0.454 m,艏摇约为-2.5°。由于管道的轴向拉力的作用,使定位精度在纵荡方向上变化了5.79倍,而管道受拖拽力影响,与托管架接触对船体产生横向力和艏摇力矩,使横荡方向上变化了1.29倍,艏摇方向上变化了1.56倍。此外,铺管工况与非铺管工况相比,船体在水平方向上的运动更加稳定,主要体现在了纵荡和艏摇方向上。
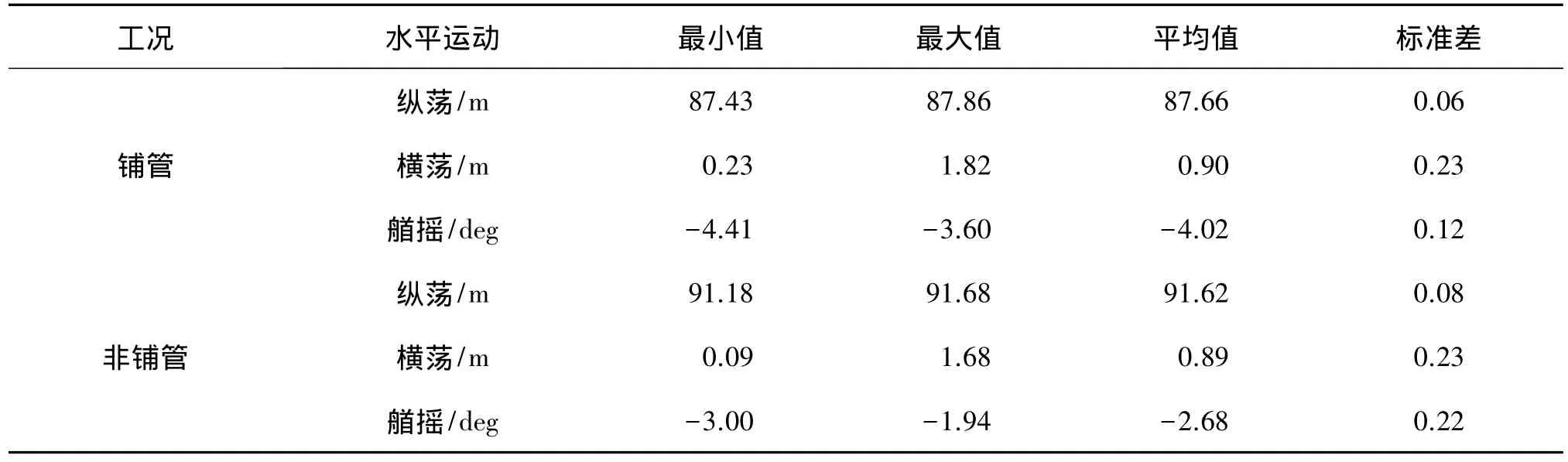
表3 铺管船水平运动时历统计数据Tab.3 The statistics of the S-lay barge horizontal motion
3.2.2 不同环境载荷,铺管工况下的动力定位时域模拟
选取各环境载荷下,纵荡、横荡以及艏摇方向偏离目标位置最大的时历曲线,如图8所示。表4给出了铺管工况下,铺管船水平运动的统计数据,选取150 s至1 000 s的数据。

表4 铺管船水平运动时历统计Tab.4 The statistics of the S-lay barge horizontal motion
由表4统计数据分析,铺管船铺管作业工况下,0°环境载荷下船体纵摇较大(见图14),对管道轴向拉力有较大的影响,从而使其纵荡方向发生了最大偏移-4.81 m。铺管船的横向环境载荷面积较大,所以在90°环境载荷下的横荡最大为3.12 m。同时,由于135°风浪流载荷作用于船体时,产生了较大的艏摇弯矩,从而造成了最大艏摇偏移量为-3.87°。此外,可以看出动力定位的控制效果相对较好,能够满足定位需求[18]。
根据功耗最小的推力分配原则,选取了0°和90°环境载荷下,各推进器推力时历曲线,如图9所示,以及功耗的时历曲线图,如图10所示。考虑到对称性,选取了1号、2号、4号、6号推进器的时历曲线。
图8 铺管船运动时历曲线Fig.8 The motion of S-lay barge
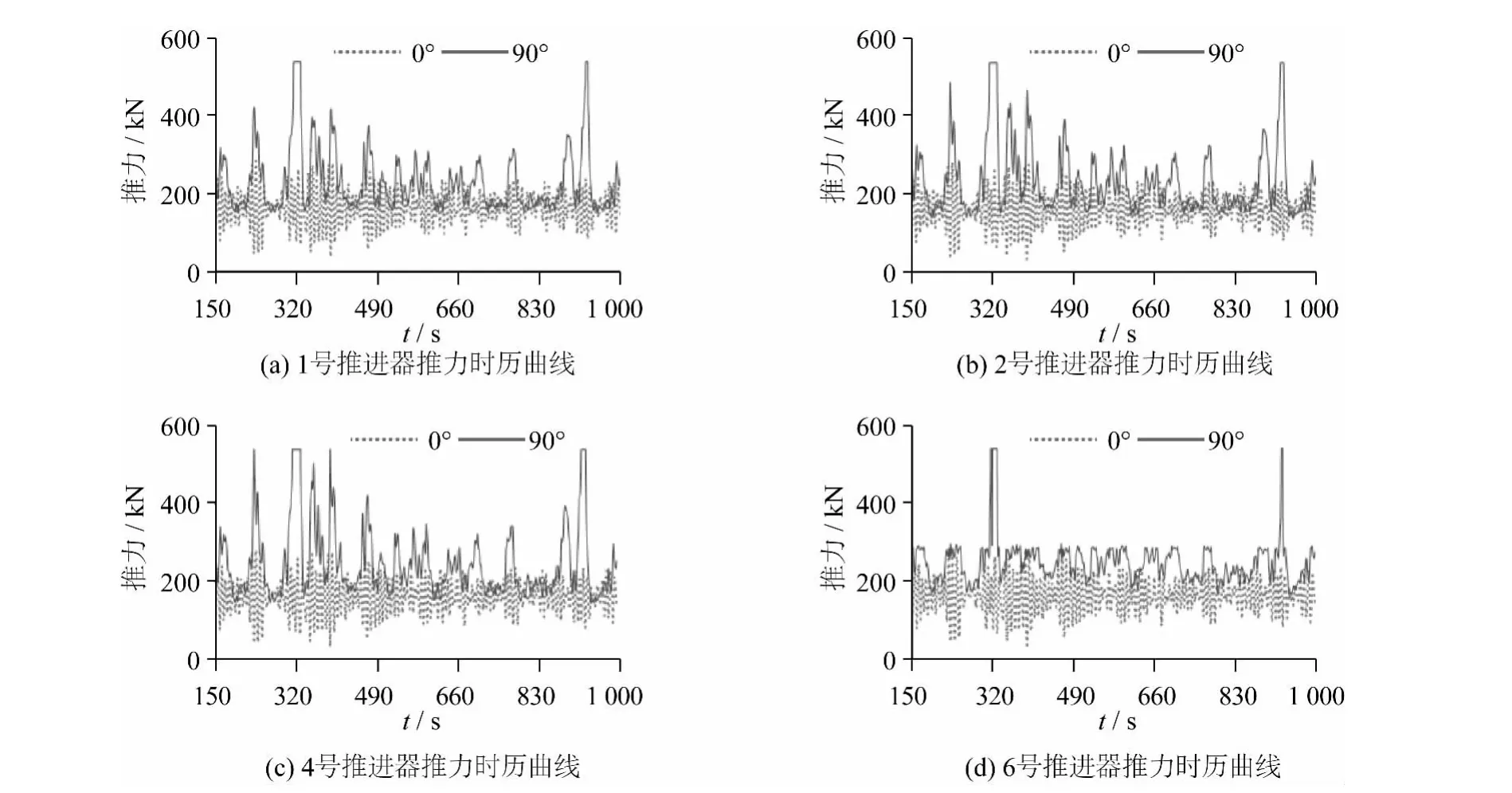
图9 各推进器推力时历曲线Fig.9 The force of thrusters
由图9和图10可知,0°环境载荷下,推进器基本维持在较为稳定的推力范围内,且功率消耗相对较小。但是铺管船环境载荷的纵向投影面积相对较大,90°风浪流载荷的作用力变化对船体影响较为明显,推进器都能达到上限推力540 kN。因此,铺管作业时应该尽量避免横向外载。
图11给出了动力定位系统在各环境载荷下消耗的总功率对比。
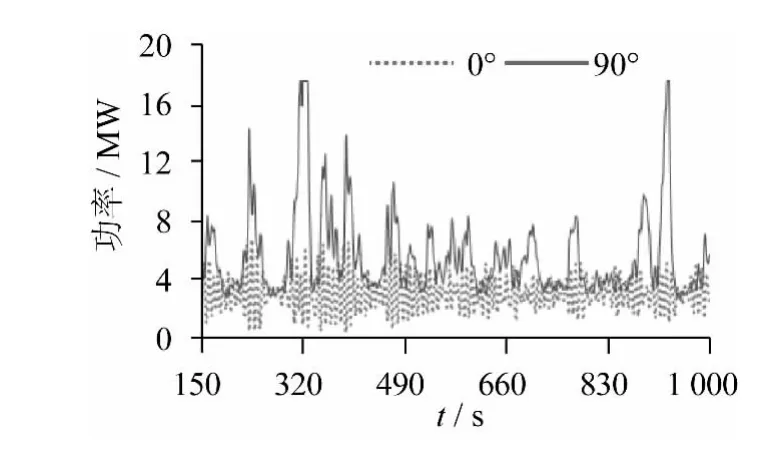
图10 总功率时历曲线Fig.10 The total power
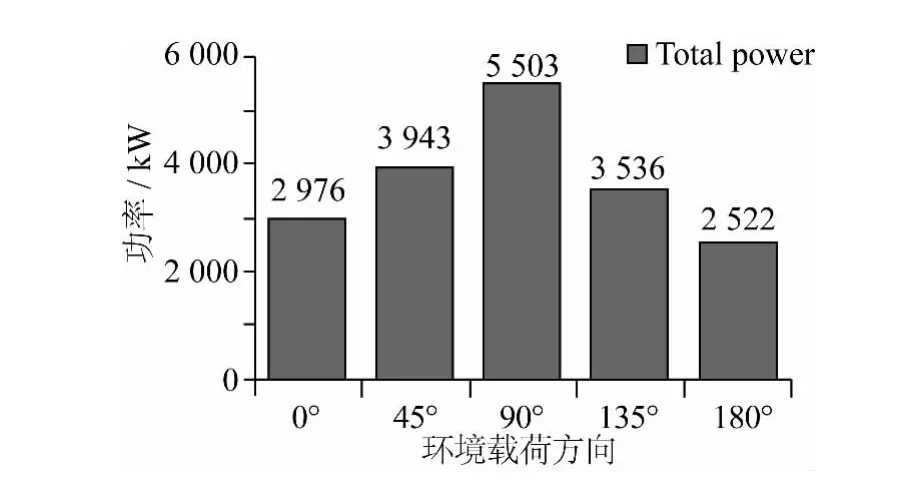
图11 动力定位系统功率消耗Fig.11 The power of dynamic positioning
由图11可知,铺管船迎浪航行铺管,对于动力定位系统而言功耗最小,均值约为2 522 kW,相比于90°环境载荷下,减少了50%左右功耗。
针对0°环境载荷和180°环境载荷动力定位系统功耗的差距,主要是因为管道对船体的作用力的影响。现对船体的垂荡、纵荡以及管道沿x方向的作用力,作如下分析。
由图12~14可知,0°环境载荷下,管道对船体的作用力均值为-1 196.94 kN,纵摇标准差为0.134,垂荡标准差为0.064。180°环境载荷下,该作用力均值约为-1 014.06 kN,纵摇标准差为0.125,垂荡标准差为0.080。这一点也印证了波频运动对管道作用力的影响,主要是在纵摇上。
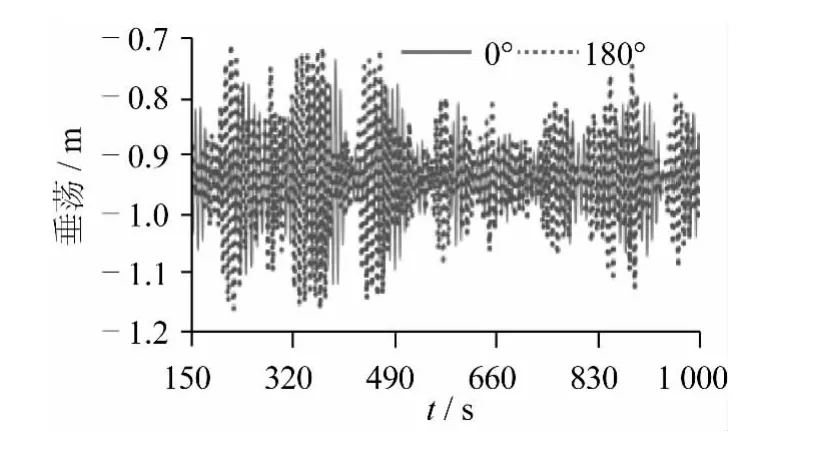
图12 船体的垂荡Fig.12 Heave motion
3.3 管线应力校核
根据API RP 2RD规范[19],普通钢制圆柱管道的von-Mises应力σAPI,可按下式进行计算:
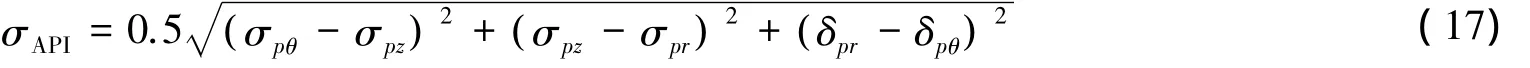
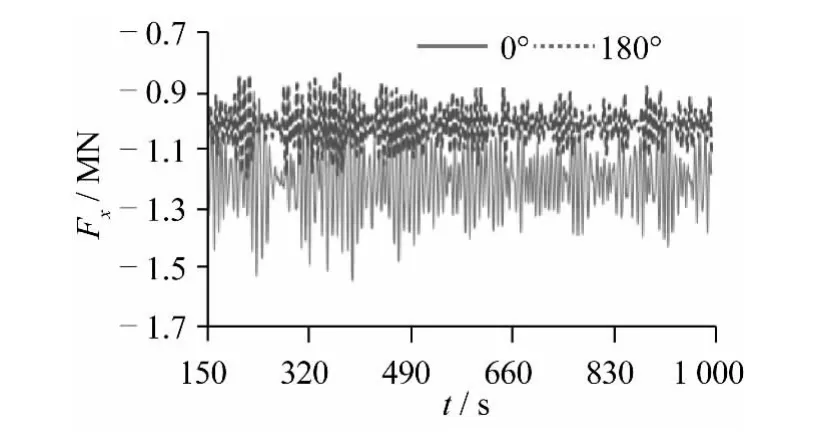
图14 管线对船体x方向的作用力Fig.14 Pipe force in x direction
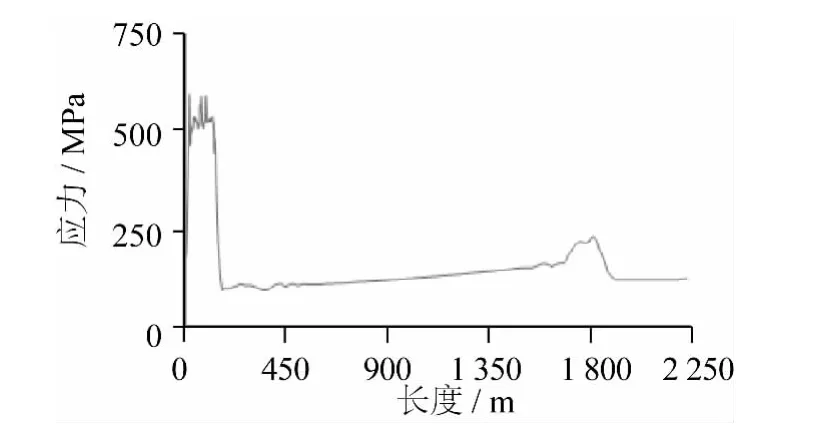
图15 管线最大应力校核曲线Fig.15 Curve of pipe maximum stress checking
对于S型铺管,普通钢制管道上弯段的弯曲应力可按如下公式计算[20]:

式中:δa为管线上弯段的弯曲应力,E为弹性模量,D为管道外径,Rcv为托管架的曲率半径。
经计算,所得管线上弯段的弯曲应力为554.55 MPa,与图15所得的最大应力586.36 MPa相差了5.4%,说明该管道和托管架耦合比较合理,有一定的准确性。
4 结语
针对S型铺管船全耦合运动,采用时下使用最为广泛的PID和Kalman滤波器相结合的定位控制系统以及最小功耗的推力分配系统,进行了全时域的动力定位系统模拟。同时,分析了波频运动对管道和托管架的耦合作用力的影响,铺管工况和非铺管工况定位系统精度的影响,以及铺管工况下,各环境载况的推力分配,以及功率的消耗。由计算分析可得如下结论:
1)波频运动对于管道作用力影响很大,对于动力定位系统而言不可忽略。在动力定位系统的作用下,波频运动的纵摇占了约85%的作用力影响,垂荡约有15%的影响。
2)铺管工况和非铺管工况相比较,动力定位系统的消耗明显增加,主要体现在纵荡和艏摇上,船体横荡相对稳定。此外,铺管工况下,船体的纵荡、横荡和艏摇运动较为稳定。
3)各环境载荷对比下,迎浪铺管是最佳铺管方式。其所受环境载荷最小,管道的轴向应力也最小,动力定位的系统消耗也最小,且能保持最优定位精度。因此,减小纵摇和迎浪铺管是使铺管作业和动力定位系统安全有效的重要方法。
[1] CHEN Haibo,MOAN T,VERHOEVEN H.Safety of dynamic positioning operations on mobile offshore drilling units[J].Reliability Engineering & System Safety,2008,93(7):1072-1090.
[2] HOLVIK J.Basics of dynamic positioning[C]//Marine Technology Society,Dynamic Positioning Conference.1998:47-50.
[3] MORGAN M J.Dynamic positioning of offshore vessels[M].United States:Petroleum Publishing Co.,Tulsa,1978:25-27.
[4] TANNURI E A,SAAD A C,MORISHITA H M.Offloading operation with a DP shuttle tanker:comparison between full scale measurenments and numerical simulation results[C]//Proceedings of the 8thIFAC Conference on Manoeuvring and Control of Marine Craft.2009:249-254.
[5] 王磊,王先福,杨建民.动力定位二阶慢漂力模型试验研究[C]//全国第七届水动力学研讨会.2005.(WANG L,WANG X F,YANG J M.Experimental research on second-order wave drift forces on a dynamic positioned ship[C]//Proceedings of 7thNational Conference on Hydrodynamics.2005.(in Chinese))
[6] 王磊,孙攀,王亮.深水半潜平台动力定位时域模拟[J].中国科学:物理学 力学 天文学,2011(2):123-131.(WANG L,SUN P,WANG L.Research on time domain simulation of dynamic positioning for a deep water semi-submersible platform[J].Scientia Sinica Physica,Mechanica& Astronomica,2011(2):123-131.(in Chinese))
[7] 闫芳,王磊,李勇跃.深水半潜式钻井平台一阶运动对动力定位控制精度的影响[J].海洋工程,2012,30(4):131-136.(YAN F,WANG L ,LI Y Y.Influence of the first-order motion of deepwater semi-submersible platform on dynamic positioning precision[J].The Ocean Engineering,2012,30(4):131-136.(in Chinese))
[8] 岳晓瑞,徐海祥,罗薇,等.海洋工程结构物风载荷计算方法比较[J],武汉理工大学学报,2011(3):454-456.(YUE X R,XU H X,LUO W,et al.Comparison of wind load calculation methods for marine engineering structures[J].Journal of Wuhan University of Technology,2011(3):454-456.(in Chinese))
[9] XU H X.Wave load calculation of deepwater vessel platform for dynamic positioning[J].IWASH,2011:265-270.
[10]孙丽萍,陈静,吴宝昌,等.半潜式平台动力定位系统推进器失效时域模拟[J].海洋工程,2013,31(3):38-44.(SUN L P,CHEN J,WU B C,et al.Time domain simulation of a semi-submersible platform with thrusters failed in dynamic positioning[J].The Ocean Engineering.2013,31(3):38-44.(in Chinese))
[11]宋林峰,孙丽萍,王德军.深水S型铺管托管架—船体—管线耦合分析[J].哈尔滨工程大学学报,2013(4):415-433.(SONG L F,SUN L P,WANG D J.Coupling analysis of stringer-lay barge-pipeline of S-lay installation in deep water[J].Journal of Harbin Engineering University,2013(4):415-433.(in Chinese))
[12]倪勤.最优化方法与程序设计[M].北京:科学出版社,2009.(NI Q.Optimization method and program design[M].Beijing:Science Press,2009.(in Chinese))
[13] SUN L P,HE Q,AI S M.Safety assessment for a side-by-side offloading system [J].Journal of Marine Science and Application,2011,10(3):315-320.
[14] RIGATOS G G.Extended kalman and particle filtering for sensor fusion in motion control of mobile robots[J].Mathematics and Computers in Simulation,2010,31(3):590-607.
[15] GONG S F,CHEN K,CHEN Y,et al.Configuration analysis of deep water S-lay pipeline[J].China Ocean Engineering,2011,25(3):519-530.
[16] Oil Companies International Marine Forum.Prediction of wind and current loads on VLCCs[M].Bermuda:[s.n.],1994:15-19.
[17] PINKSTER J A.Low frequency second order wave exciting forces on floating structures[M].Marine Publication,1980:650.
[18] SORENSEN A J,LEIRA B,STRAND J P.Optimal set point chasing in dynamic positioning of deep-water drilling and intervention vessels[J].Int.J.Robust Nonlinear Control,2001:1187-1205.
[19] API RP ZRD,Design of risers for floating production systems and TLPs[S],2006:53-54.
[20] GUO Boyun,SONG Shanhong,GHALAMBOR A,et al.Offshore pipelines[M].2014:13-20.

