一种频域亚像元影像匹配方法

王恺 陈世平 曾

（1 北京空间机电研究所，北京 100094）

（2 中国空间技术研究院，北京 100081）

（3 中国资源卫星应用中心，北京 100094）

0 引言

摄影测量中控制点的提取是摄影测量系统检校的基础，也是提取物体三维信息的基础。在数字摄影测量中以影像匹配代替传统的人工观测，可以达到自动确立同名像点的目的[1]。影像匹配分为基于模板和基于特征的两种方法。基于模板的影像匹配方法又分为灰度相关法、相位相关法和互信息法等[2]。由于相位相关法计算速度快，对变化成像条件或频域噪声有很高的鲁棒性，适合于航天遥感摄影测量，是本文将要研究的方法。

文献[3]于 1975年提出了相位相关匹配方法，但只能求解出两函数间的整数级平移；文献[4-5]通过对相位相关函数进行多相位分解，将相位相关法扩展到亚像元级，但如果待匹配影像存在严重混叠时，匹配误差很大；文献[6]分析了混叠对相位匹配的影响，并对相位相关函数首先进行掩模处理，将相位差平面中受混叠影响较大的点去除，然后使用最小二乘法在频域中直接求解平移分量；文献[7]指出无噪声相位相关函数是一个秩1矩阵，可以使用奇异值分解得出有噪声相位相关函数的一个秩1子空间，进而对其在频域中使用最小二乘法求解平移分量，这种方法对噪声和混叠都有较高的鲁棒性和精度，但计算量较大；文献[8]在相位差求解过程中使用快速最大概率密度功率法来估计平移参数，在计算速度和可靠性间取得了一定平衡；文献[9]引入两点梯度法来求解平移参数，可靠性较高，运算速度较快。

从相位相关法的发展可见，其大致可分为两类：空域Dirac Delta函数法和频域直接求解法。前者计算过程简单快速，对噪声抑制性好，但只能求出整数像元的平移[3]，后经改进，虽然可以实现亚像元匹配，但受混叠影响大[9]；后者计算过程复杂，匹配结果的可靠性较前者低，但可以在一定噪声、混叠存在的情况下实现高精度匹配。为了实现影像精确、可靠地匹配，本文提出一种将上述两种方法有机结合的频域匹配新方法：优化相位匹配法，先使用空域Dirac Delta函数法进行粗匹配，然后使用频域直接求解法进行精匹配，并且在精匹配时使用优化法，进一步提高了算法的精度和可靠性。

1 优化相位匹配的原理

则

为实现亚像元精度的匹配，采用在频域直接求解相位差平面斜率的方法。使用这种方法的关键有两点：1）要正确地找出属于相位差平面的点集；2）通过此点集估计出相位差平面斜率参数。

对输入影像加窗及傅里叶变换后，按照式（5）计算相位相关函数，进而得到相位差。如果输入影像中存在混叠，不等于，即幅值并不等于 1[6]。可以将的幅值作为衡量混叠大小的标志，幅值越接近1，受混叠影响越小。据此得权函数为

式中 参数α通过实验确定，具体方法见参考文献[6]。将权函数与相乘，即可求得受混叠影响较小的属于相位差平面的点集。

以上得到的相位差位于[- π ,π]之间，相位差面并非平面，相位差是缠绕的。文献[11-12]给出此时的相位差为

式中 r、c为相位差矩阵的行列标号；M、N为行列数；J为任意整数。为了得到相位差平面，需要进行相位差解缠绕。根据式（7）、（8），相位差矩阵可以按行或列进行解缠绕，从而将二维解缠绕简化为一维解缠绕。解缠绕前需要对相位差滤波去噪，去噪效果直接决定解缠绕的品质[13]。如果要实现优良的去噪效果，则需针对具体影像的相位差设计滤波器。

2 算法实现

根据上述算法原理，先使用空域 Dirac Delta函数法对两幅影像进行粗配准，得出整数级别的平移，真实平移必定位于中，再通过以上的优化法求取最佳亚像元平移估计值，算法流程如图1所示。

整个算法如下：

3）在参考影像上截取子影像 p1，p1左上角在原影像中的位置为，大小为×；在待匹配影像上截取子影像p2，p2左上角在原影像中的位置为(0, 0)，大小为；

4）对p1和p2使用Blackman-Harris窗进行加窗处理，对处理后的影像进行傅里叶变换得和；

图1 算法流程图Fig.1 Flow chart of the algorithm

3 实验验证

为了验证算法的匹配精度，本文采用0.5m分辨率的航空影像表征地面真实情况，通过滤波和降采样生成待匹配影像对。如果待匹配影像对在原高分辨率影像中的平移差为，降采样率为 l，则降采样后待匹配影像对理论平移差为。选择42幅航空影像，影像内容为村庄、农田、湖、山等，每种影像7幅，每幅影像大小为256×256像元，每像元的量化位数为8bit。降采样率l可取任意值，本文取为4。或取整数值-2～1像元。为了测试不同混叠程度下的算法精度，采用高斯低通滤波器对原图像进行滤波，空域高斯核函数的“标准差”σ取值为{1.0, 1.5, 2.0, 2.5, 3.0}，模板大小为9×9像元，对应频域带宽为{0.477 5,0.318 3,0.238 7,0.191 0,0.159 2}。标准差越大，降采样后影像中的混叠越小，降采样后共生成3 360幅影像。

表1、2分别列出不同景物影像在不同混叠时的平均匹配误差和最大匹配误差，混叠越小、景物细节越丰富，则匹配误差越小。纹理不丰富的场景，如农田等，随着滤波器带宽变窄，降采样后图像中的混叠变少，匹配误差随之变小。当高斯滤波器带宽较小、降采样后图像纹理减少较多时，匹配误差随着带宽的减小反而由减小变为增大，见表1、2中σ=3时的情况。对基本无纹理的场景，如湖水等，自身高频分量较少，匹配误差随着滤波器带宽的减小没有显著下降。当混叠较小时（σ=3），基本无纹理的场景匹配误差优于1/10个像元；纹理不丰富的场景匹配误差优于1/20像元；纹理丰富的场景（如村庄等）匹配误差优于1/100像元。

表1 平均匹配误差Tab.1 The average matching errors 像元

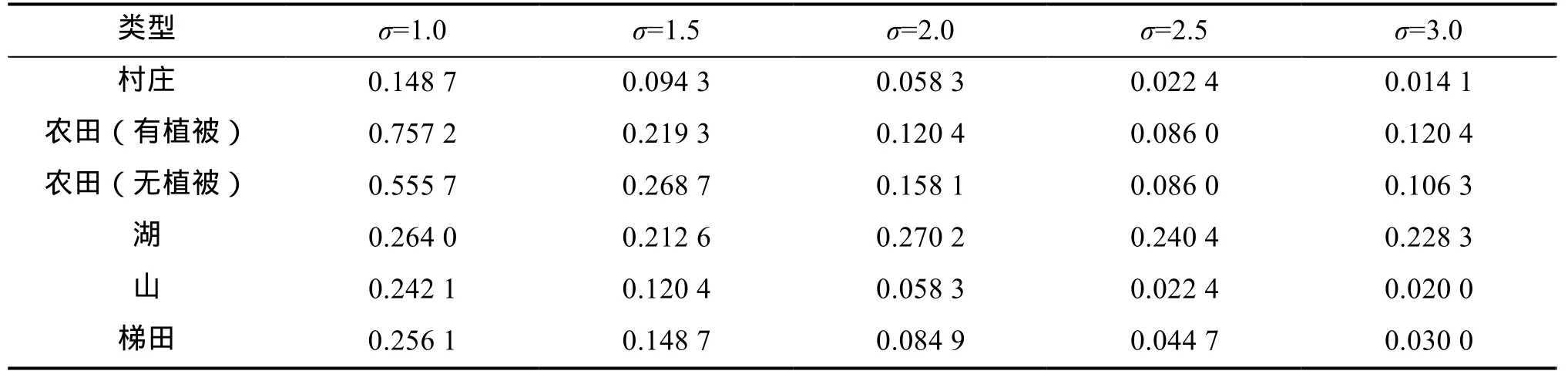
表2 最大匹配误差Tab.2 The maximum matching errors 像元

不同信噪比下算法的匹配误差见表3。场景选择为村庄，共7幅高分辨航空影像，每幅影像大小为256×256像元，降采样率l=4，δx或δy取整数值-2～1，高斯滤波器σ=3，降采样后图像加入高斯白噪声，共生成 560幅待匹配影像。随着信噪比（采用峰值信噪比，PSNR）增大，匹配误差随之减小。当PSNR＞30dB，匹配误差受PSNR影响较小，算法对存在噪声的影像的匹配性能较好。

其他研究者的相位匹配算法的匹配误差见表4。场景选择为村庄，共7幅高分辨航空影像，每幅影像大小为 256×256像元，降采样率 l=4，δx或 δy取整数值-2～1，高斯滤波器 σ=3，降采样后图像加入高斯白噪声（PSNR=30dB），共生成112幅待匹配影像。除了COSI-Corr算法匹配精度和本文相近外，其他算法的精度都相对较低。在实验中发现，COSI-Corr算法有时会出现不收敛的情况，可靠性比本文提出的算法低。

表3 不同峰值信噪比下的匹配误差（σ=3）Tab.3 The matching errors in the different PSNR（σ=3）像元

表4 不同相位匹配算法的匹配误差（σ=3，PSNR=30dB）Tab.4 The matching errors about the different phase matching methods（σ=3，PSNR=30dB）像元

4 结束语

经以上实验验证，本文提出的匹配方法对混叠有一定的抑制能力，对噪声有较强的鲁棒性。对于纹理丰富的、存在少量混叠的影像匹配误差优于1/100个像元。本方法是一种高精度的、可靠的影像匹配方法，可以将其应用到数字摄影测量软件中实现高精度、高可靠性地确定同名像点。

References)

[1]张祖勋, 张剑清. 数字摄影测量学[M]. 武汉: 武汉大学出版社, 2012.ZHANG Zuxun, ZHANG Jieqing. Digital Photogrammetry[M]. Wuhan: Wuhan University Press, 2012. (in Chinese)

[2]Barbara Z, Jan F. Image Registration Methods: A Survey[J]. Image and Vision Computing, 2003, 21(11): 977-1000.

[3]Kuglin C D, Hines D C. The Phase Correlation Image Alignment Method[C]. In Proc. Int. Conf. on Cybernetics and Society.New York: IEEE, 1975:163-165.

[4]Shekarforoush H, Berthod M, Zerubia J. Subpixel Image Registration by Estimating the Polyphone Decomposition of Cross Power Spectrum[C]. IEEE Computer Society Conference on Computer Vision and Pattern Recognition, 1996: 532-537.

[5]Foroosh H, Zerubia J, Berthod M. Extension of Phase Correlation to Subpixel Registration[J]. IEEE Trans. Image Process,2002, 22(2): 188-200.

[6]Stone H S, Orchard M, Change E C, etal. A Fast Direct Fourier-based Algorithm for Subpixel Registration of Images[J].IEEE Trans. Geosci. Remote Sensing, 2001, 39(10): 2235-2243.

[7]Hoge W S. A Subspace Identification Extension to the Phase Correlation Method[J]. IEEE Trans. Medical Imaging, 2003,22(2): 277-280.

[8]Liu J G, Yan H S. Robust Phase Correlation Methods for Sub-pixel Feature Matching[C]. lst SEAS DTC Technical Conference. Edinburgh, 2006.

[9]Leprince S, Member S, Ayoub F, etal. Automatic and Precise Ortho Rectification, Coregistration, and Subpixel Correlation of Satellite Images, Application to Ground Deformation Measurements[J]. IEEE Trans. Geosci. Remote Sensing, 2007,45(6): 1529-1558.

[10]Fredric J H. On the Use of Windows for Harmonic Analysis with the Discrete Fourier Transform[J]. Proceedings of the IEEE, 1978, 66(1): 51-83.

[11]Murat B, Hassan F. Inferring Motion From the Bank Constraint of the Phase Matrix[J]. IEEE ICASSP 2005 Proc., 2005(2):925-928.

[12]Murat B, Hassan F. Estimating Subpixel Shifts Directly from the Phase Difference[C]. ICIP, 2005: 1057 -1060.

[13]Dennis C G, Mark D P. Two-dimensional Phase Unwrapping Theory, Algorithms and Software[M]. New York: John Wiley amp; Sons Inc., 1998.