重力空射稳定伞阻力特征自动化设计

尹凯 张红英 陈建平 童明波

（南京航空航天大学航空宇航学院，南京 210016）

0 引言

内置式重力空射是由载机将火箭置于机舱内带至高空，以重力为主、稳定伞为辅的空中发射火箭的方法[1-2]，其基本流程如图1所示。飞机以一定仰角巡航，火箭出舱时尾部先落下而头部后落下，在重力作用下火箭会绕质心作俯仰运动；而稳定伞的作用就是产生适当阻力控制俯仰运动，当俯仰角速度接近于零时，火箭达到发射俯仰角，火箭点火并切断连接绳。由于火箭发射时的俯仰角、高度和速度完全由稳定伞决定，因此选取具有合适阻力特征的稳定伞就显得至关重要。当进行投放试验时，回收试验火箭以获取试验数据很有必要。试验火箭回收方式如图2所示。对于投放试验，当达到发射俯仰角时，试验火箭并不点火，此时有切断连接绳和不切断连接绳两种回收方式。不同的回收方式对火箭最终落地状态影响较大。

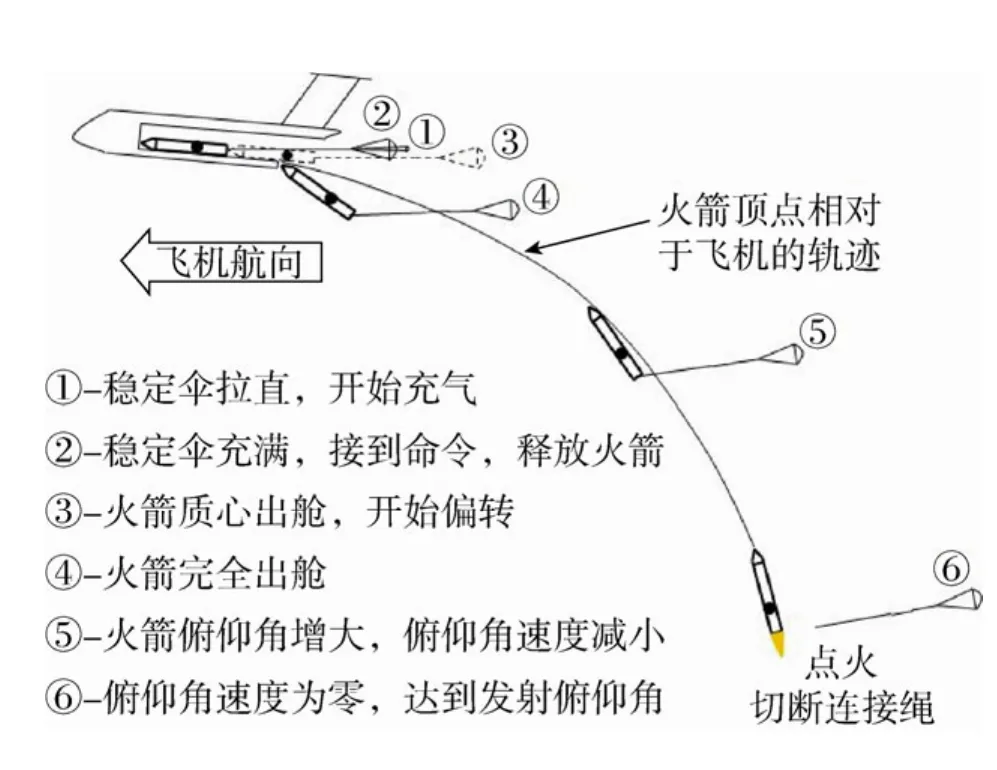
图1 内置式重力空射稳定伞的工作流程Fig. 1 Working process of stabilizing parachute for GAL

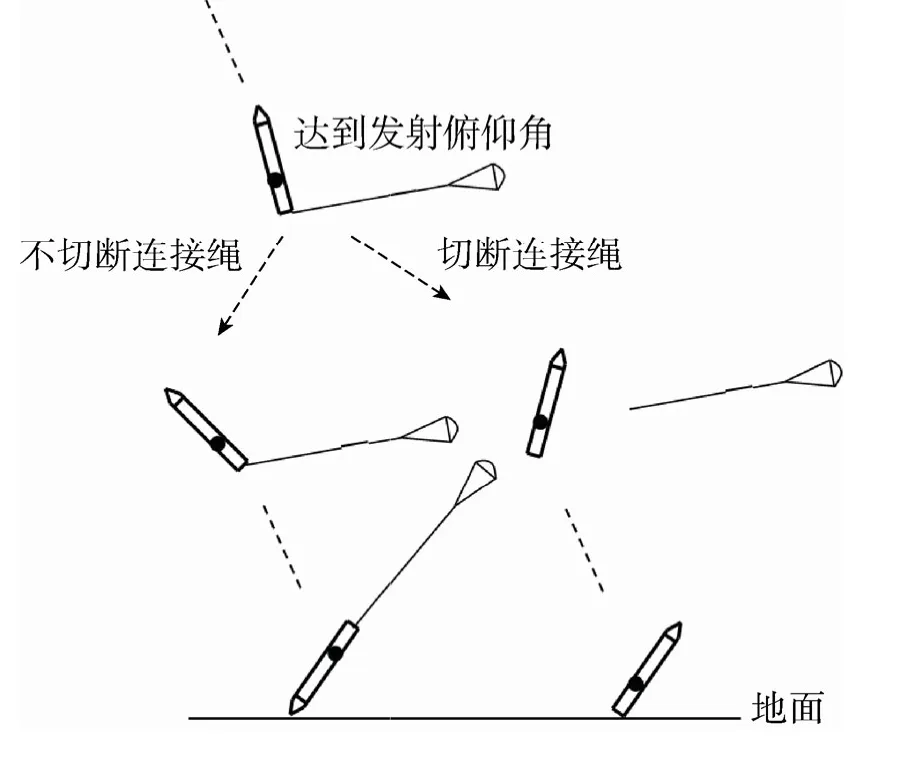
图2 试验火箭回收方式 Fig. 2 Recovery method of test rocket

通常火箭发射俯仰角由空射总体方案给出，目前国内外现有的文献都是在给定的参数下，通过不断试算来获取合适的稳定伞阻力特征，该方法既费时又费力[3-4]。本文基于多体动力学软件（ADAMS），构建了火箭和稳定伞的动力学模型，通过动态链接子程序实现了气动力的加载，研究从稳定伞充气完成到试验火箭落地之间的整个系统的运动全过程。对于每个给定的发射俯仰角，应用可行方向优化算法实现了稳定伞阻力特征的自动化设计，为空射总体方案设计提供了参考。

1 动力学模型

由于ADAMS软件可自动建立求解动力学方程，因此本文动力学建模重点在于施加合适的力与约束来模拟重力空射过程。一般重力空射根据受力情况可分为3个阶段，如图3所示。

图3 重力空射受力分析Fig.3 Force analysis of GAL

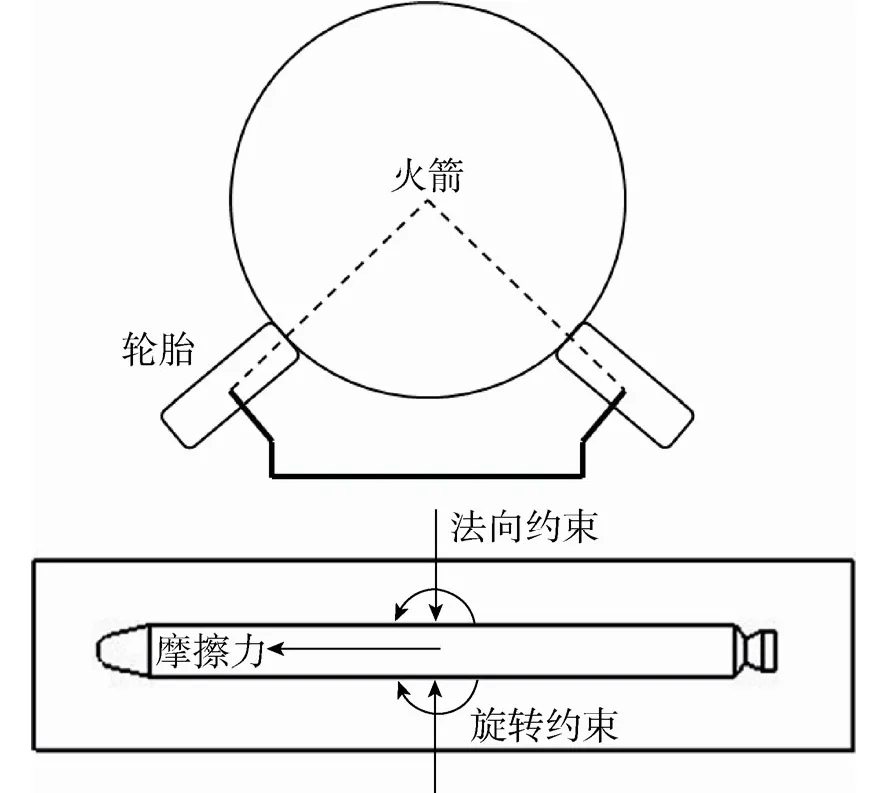
图4 传送轮胎及其反作用力简化Fig.4 Forces and constraints from tires

第一阶段，火箭完全在舱内运动，受重力、传送轮胎（如图4）的反作用力及连接绳拉力的作用，其中轮胎对火箭在飞机对称平面内的作用可简化为接触力与相应的摩擦力，接触力采用 Impact冲击力模型，轮胎对火箭的横向固定作用可简化为作用在火箭质心上的法向约束和对箭体的旋转约束（如图4所示），连接绳拉力可通过质量弹簧阻尼模型来施加[5]；稳定伞受重力、气动力和连接绳拉力作用，气动力通过子程序施加。

第二阶段，火箭质心出舱，火箭开始偏转，此时火箭还部分受到气动力的作用，可通过子程序施加。

第三阶段，火箭完全出舱，此时轮胎反作用力取消，火箭全体受气动力的作用。

2 气动力模型

火箭和稳定伞所受的气动力比较复杂，ADAMS软件中没有相应的模块。现有的文献当中大部分是通过和 Matlab联合仿真来计算气动力[6]，这样计算较慢且限制较大。本文通过 ADAMS接口文件GFOSUB，自编动态链接库子程序实现了气动力的快速计算。

2.1 火箭气动力模型

由于火箭是轴对称形状，为方便气动力的计算，采用总攻角和气动滚转角，连体坐标系原点为火箭质心，如图5所示。图中，、、为火箭质心空速在火箭连体坐标系上的分量，可在子程序中通过功能函数获得；为火箭质心总空速；LF和DF为总升力和总阻力；θ为总迎角；φ为气动滚转角；C为火箭质心。气动力可根据实验所得气动系数插值得到，气动力矩可根据火箭质心和压心的相对位置求出。由于火箭在整个运动过程中的角速度很小，因此不考虑角速度对气动力和气动力矩的影响。最后将求得的力和力矩分解到火箭连体坐标系上。

2.2 稳定伞气动力模型

在子程序中可以通过功能函数获取稳定伞气动中心（简化为与质心C重合）在全局坐标系的空速分量，稳定伞受到的气动力为，方向与总空速方向相反，稳定伞中轴线始终沿着总空速方向，如图6所示。式中，ρ为稳定伞高度处的大气密度，可在子程序中插值得到； Vac为稳定伞质心的总空速；CA为稳定伞阻力特征[7]。最终将求得的气动力分解到全局坐标系上。

图5 火箭气动力模型Fig.5 Aerodynamic force model of rocket

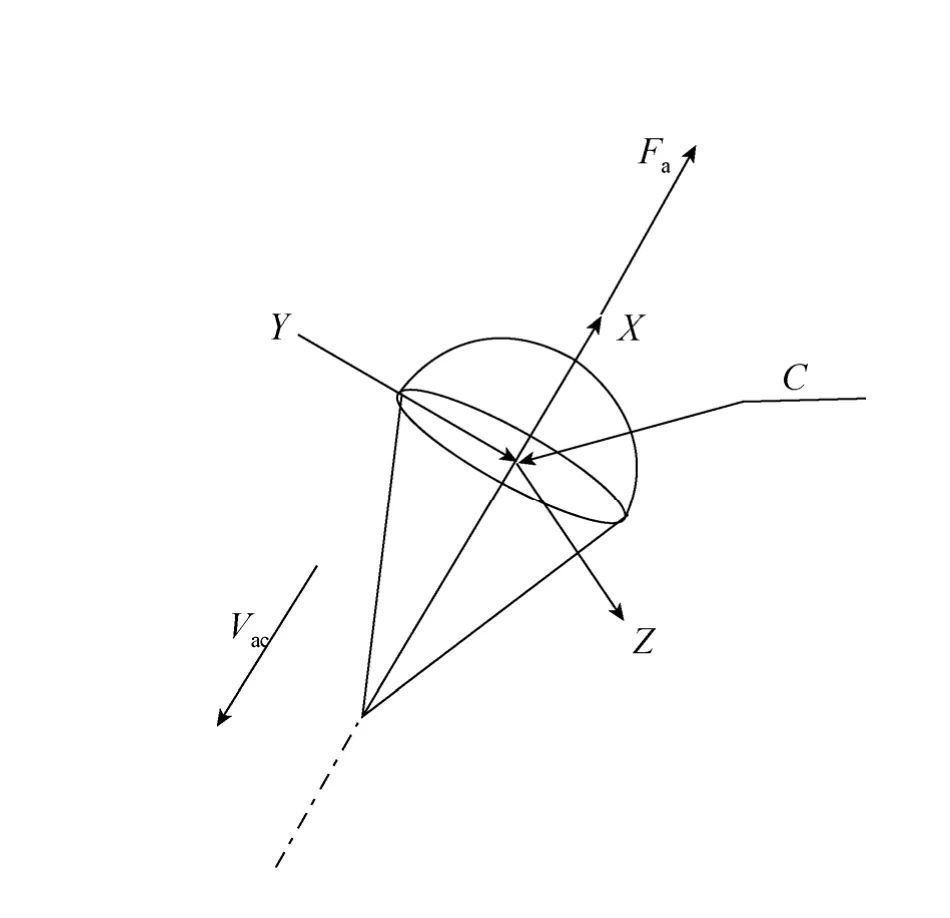
图6 稳定伞气动模型Fig. 6 Aerodynamic force model of stabilizing parachute

3 参数化建模及稳定伞阻力特征自动化设计

仿真中需要根据总体方案要求不断地更改模型，费时费力，通过参数化建模和优化算法可简化设计流程。

3.1 参数化建模

采用ADAMS命令语言，编制交互界面，通过参数化建模可方便地修改模型[8]，如图7所示。

图7 参数化建模用户界面Fig. 7 User interface of parameterized model

3.2 稳定伞阻力特征自动化设计

在模型参数设置好的情况下，欲使火箭达到总体方案给定的发射俯仰角，就需要设置一个合适的稳定伞阻力特征。目前国内外现有的文献都是在给定的参数下，通过不断试算来获取合适的稳定伞阻力特征，该方法既费时又费力。考虑到收敛的快速性，本文基于ADAMS优化算法接口文件vc_init_usr，采用可行方向优化算法，在模型参数设置好的情况下，给定一个发射俯仰角，该算法能自动逆推出达到该发射俯仰角所需的稳定伞阻力特征，从而简化了设计流程[9]。

可行方向法是一个直接数值优化方法，它可在搜索空间的某个方向上不断寻求最优解，相较于ADAMS自带优化方法，该方法能更加快速的达到目标值[10]。其一般形式如下所示：

通过负梯度法、优选法构造可行下降方向，如下式所示：

式中 xk为第k个可行点；为函数在 xk处的梯度； sk为第k个可行点处的可行方向；｝为点 xk处起作用约束的指标集。

在可行方向ks确定以后，通过盲人探路法获取下一个可行点，如此循环迭代直到获取一个最优解。

令α（ C A）为稳定伞阻力特征取CA，火箭出舱后俯仰角速度第一次为零时的俯仰角（即发射俯仰角），αd为火箭的期望发射俯仰角。则取目标函数，如图8所示。约束函数也取为选取合适的阻力特征CA的初始值，经过可行方向算法迭代，最终可以得到

式中dCA 即为达到期望发射俯仰角所需的稳定伞阻力特征。

通过用户界面，可方便地进行优化计算，如图9所示。

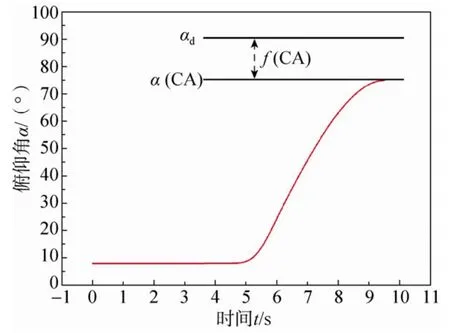
图8 目标函数Fig.8 Objective function

图9 优化分析用户界面 Fig.9 User interface of optimizing and analysis

4 仿真计算结果分析

取试验火箭质量为 6t，火箭与传送轮胎间的摩擦系数为 0.1，投放高度为 8km，飞机巡航速度为120m/s，且以6º仰角飞行时，通过自动优化设计得到65º～90º发射俯仰角所对应的稳定伞阻力特征，如图10所示。

图11为发射俯仰角与火箭出舱时间和到达发射俯仰角所用时间关系，从图中可以看出，火箭发射俯仰角越大，所需稳定伞阻力特征越小，箭头出舱所用时间增大，到达发射俯仰角所用时间也延后。

图10 发射俯仰角与相应稳定伞阻力特征Fig.10 Parachute drag area vs launching pitch angle

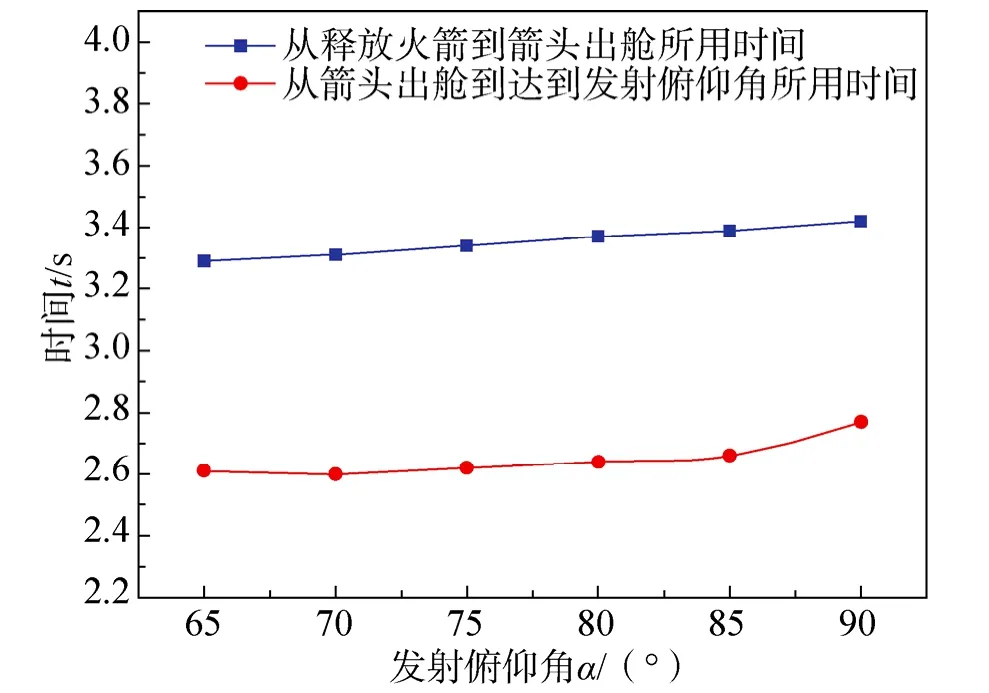
图11 发射俯仰角与相应时间Fig.11 Time vs launching pitch angle

火箭在出舱过程中要保证箭头不与飞机相碰，如图12所示。图13显示了火箭出舱过程中，火箭安全距离（火箭出舱过程中箭头离飞机货舱上壁板的最小距离）与发射俯仰角的关系，从图中可得，随着发射俯仰角的增大，稳定伞阻力特征减小，火箭箭头在出舱过程中与飞机相碰的可能性增大。

图12 火箭出舱图Fig.12 Rocket going out of aircraft

图13 发射俯仰角与相应安全距离Fig.13 Safety distance vs launching pitch angle

试验火箭达到发射俯仰角时并不点火发射，为获取实验数据，应当将其回收，回收有两种方式（见图2），一种是保留稳定伞，当达到俯仰角时，不切断连接绳；另一种是不保留稳定伞，当到达发射俯仰角时，切断连接绳，让试验火箭自由下落。在实验火箭的发射俯仰角取为80º的情况下（稳定伞阻力特征为2.68m2），火箭回收过程中，两种不同的回收方式对应的实验火箭水平移动距离，如图14和图15所示。

图14 保留稳定伞时试验火箭水平移动距离Fig. 14 Horizontal displacement of test rockt when stabilizing parachute is remained

图15 不保留稳定伞时试验火箭水平移动距离Fig. 15 Horizontal displacement of test rockt when stabilizing parachute is not remained

火箭回收过程中，两种不同的回收方式对应的火箭俯仰角变化如图16和图17所示。

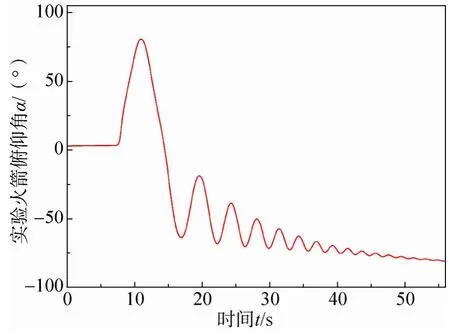
图16 保留稳定伞时试验火箭俯仰角变化Fig.16 Pitch angle of test rockt when stabilizing parachute is remained

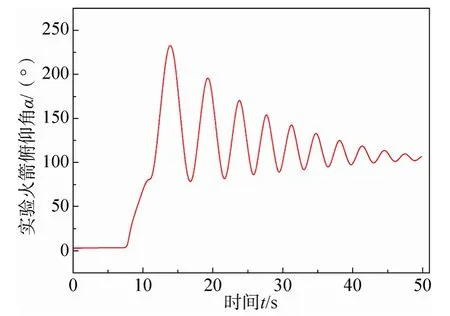
图17 不保留稳定伞时试验火箭俯仰角变化 Fig.17 Pitch angle of test rockt when stabilizing parachute is not remained

从图中可以看出，两种回收方式对实验火箭落地时的水平位移影响不大，但对火箭落地时的俯仰角影响较大。这是由于稳定伞在实验火箭出舱阶段主要起的是一个姿态调整的作用，因此其阻力特征相对较小，对后续实验火箭回收阶段的水平减速效果不明显。在保留稳定伞的情况下，由于稳定伞的拖拽作用，实验火箭落地时，其俯仰角为负，即箭头着地；在不保留稳定伞的情况下，实验火箭落地时，其俯仰角为正且超过 90º，即箭尾着地。这对试验数据的存放位置有一定的参考意义，为避免与地面的直接碰撞，当保留稳定伞时，试验数据应存放在箭尾；当不保留稳定伞时，试验数据应存放在箭头。

5 结束语

本文以多体动力学软件ADAMS为二次开发平台，构建了重力空射的动力学仿真模型。推导了火箭和稳定伞的气动模型，并通过编写动态链接子程序实现了气动力的加载；通过参数化建模与自编可行方向优化算法实现了稳定伞阻力特征的自动化设计，简化了设计流程。最后，通过一个具体的算例，验证了方法的可行性，得到了关于空射稳定伞以及实验火箭回收方式的一些有意义的结果，为重力空射的总体方案设计提供了参考。由于本文是进行稳定伞的初步设计，因此只考虑到对整个空射系统影响最重要的阻力特征，在阻力特征定下来的情况下，具体的稳定伞细节设计还需进一步的工作。

References)

[1]Sarigul K M, Sarigul K N, Hudson G C, etal. Flight Testing of a Gravity Air Launch Method to Enable Responsive Space Access[C]. 45th AIAA Aerospace Sciences Meeting and Exhibit, AIAA 2007-6146,2007.

[2]Sarigul K M, Sarigul K N, Hudson G C. Gravity Air Launching of Earth-to-orbit Space Vehicles[C]. 46th AIAA Aerospace Sciences Meeting and Exhibit, AIAA 2008-5137, 2008.

[3]Fritz D, Webber C. Falcon Quick Reach-airdrop Envelope Expansion to Enable Low Cost Space Access[C]. Symposium Proceedings-society of Experimental Test Pilots, 2006, 50-159.

[4]Hudson G C. Quickreach Responsive Launch System[C]. 4th Responsive Space Conference, Los Angeles, 2006.

[5]郭叔伟, 董杨彪, 秦子增. 物伞系统动力学模型和讨论[J]. 航天返回与遥感, 2008, 29(3): 38-44.GUO Shuwei, DONG Yangbiao, QIN Zizeng. The Parachute System Dynamics Model and Discussion[J]. Spacecraft Recovery amp; Remote Sensing, 2008(3): 38-44.(in Chinese)

[6]常立平, 唐硕, 许志. 内装式空射火箭发射前姿态控制方法研究[J]. 科学技术与工程, 2012,20(9): 2100-2104.CHANG Liping, TANG Shuo, Xu Zhi. Attitude Control Method of Rocket before Launching for Internal Gravity Air Launch[J]. Science Technology and Engineering, 2012, 20(9): 2100-2104. (in Chinese)

[7]王利荣, 吴剑萍. 降落伞理论与应用[M]. 北京: 宇航出版社, 1997: 121-130.WANG Lirong, WU Jianping. Parachute Theory and Application[M]. Beijing: Aerospace Press, 1997: 121-130. (in Chinese)

[8]孙良, 赵匀, 张玮炜. ADAMS二次开发技术在分插机构设计中的应用[J]. 浙江理工大学学报, 2011, 28(3): 389-393.SUN Liang, ZHAO Yun, ZHANG Weiwei. ADAMS Secondary Development in the Design of Transplanting Mechanism[J].Journal of Zhejiang Institute of Science and Technology, 2011, 28(3): 389-393. (in Chinese)

[9]田媛媛. 基于ADAMS和遗传算法的汽车悬架系统优化和分析[D]. 哈尔滨: 哈尔滨工业大学, 2009.TIAN Yuanyuan. Optimization and Analysis about Vehicle Suspension System based on ADAMS and Genetic Algorithms[D]. Harbin: Harbin Institue of Technology, 2009. (in Chines)

[10]李春明. 优化方法[M]. 南京: 东南大学出版社, 2009: 107-113.LI Chunming. Optimization Method[M]. Nanjing: Southeast University Press, 2009: 107-113. (in Chinese)