基于子孔径拼接的超大型光学遥感器检测技术

赵号 王红杰 李博

（北京空间机电研究所，北京 100094）

0 引言

高分辨率的空间光学遥感器代表着空间遥感技术领域的制高点[1]。由于光学遥感器的空间分辨率受光学系统衍射极限的限制，因此增大光学系统的口径是提高光学遥感器空间分辨率的一条有效途径。目前，超大型光学遥感器已成为空间遥感载荷发展的一个主流方向[2-3]。对于超大型光学遥感器，若采用常规方法进行系统检测，难度大、成本高，而使用子孔径拼接检测法可以有效解决这一问题。

子孔径拼接法在进行检测时将被检区域划分为重叠的有限个子孔径，通过子孔径数据的拼接计算获得全口径波前信息[4-6]。子孔径检测技术于20世纪80年代提出，先后经历了基于Zernike多项式描述波前算法、离散相位值描述波前算法、多子孔径重叠扫描技术和拼接干涉仪工作站等阶段[7-11]。目前，子孔径拼接检测技术发展迅速，但是对该技术的研究多集中于对光学镜面的检测[12-14]，对其在光学系统波前检测方面的应用研究较少。

1 检测原理

自准直检测法是一种常用的光学遥感器系统检测方法，需要与系统口径相当甚至更大的自准直平面镜。检测时，干涉仪放置于待检测光学系统焦面处，其发出的检测光束入射到光学系统后平行出射，经与光轴垂直的自准直平面镜反射后重新进入光学系统，最终被干涉仪接收，经处理可以得到系统的波前信息。超大型光学遥感器具有超大口径、超长焦距、比刚度高等特点，利用自准直检测法进行系统检测时，为了避免超大口径自准直镜的研制，可以使用小口径自准直平面镜代替全口径自准直镜。检测过程中，通过子孔径自准直平面镜位置的变化实现光学系统全口径的覆盖，每次检测整个系统的一部分，各子孔径之间存在重叠部分，根据重叠区数据的一致性原则，可以进行全口径波前的重构。为了规避重力的影响，检测时采用光轴竖直的检测方式。子孔径拼接法检测超大型光学遥感器的原理如图1所示，其中待检测光学系统是一个主镜与次镜均为双曲面的RC系统。

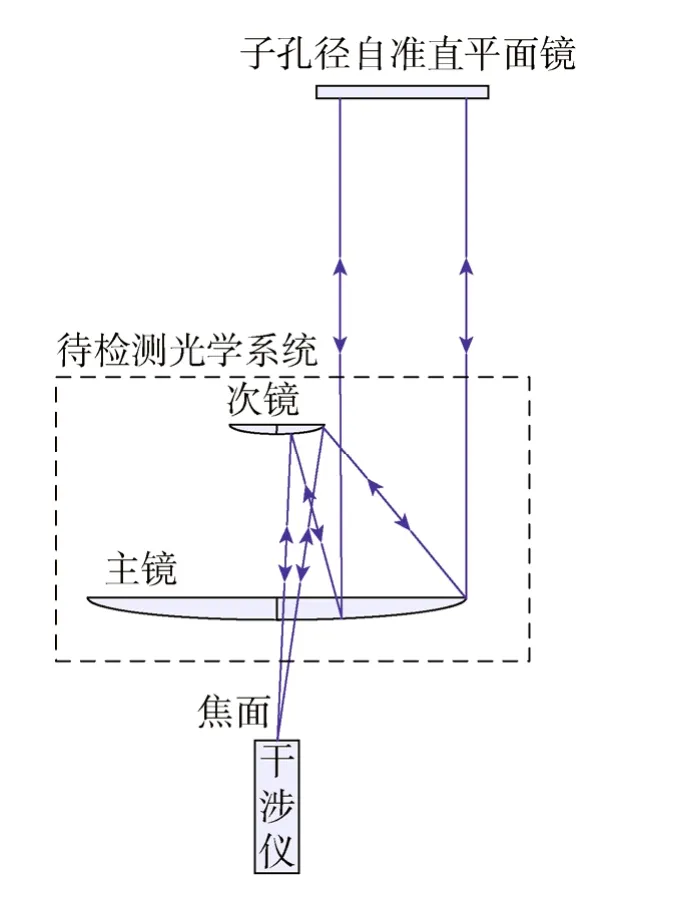
图1 子孔径拼接法检测超大型光学遥感器原理Fig.1 Principle of testing super large optical remote sensor by sub-aperture stitching interferometer

1.1 子孔径布局

子孔径的布局与子孔径分布方式、子孔径口径、子孔径重叠区面积、待检测光学系统口径及其中心遮拦口径有关。子孔径单圈中心对称分布时子孔径间的几何关系如图2所示。

图中，OA为待检测光学系统半径，长度为R；OB为中心遮拦半径，长度为t；O1A为子孔径半径，长度为r；OO1为子孔径中心所在圆半径，长度为ρ。若要求两子孔径重叠区与单个子孔径的面积比为ε，则设∠BO1O的角度为θ，所需的子孔径个数为n，根据两子孔径重叠区与单个子孔径的面积关系及三角正弦定理，可得θ与n满足关系：

图2 子孔径间的几何关系Fig.2 Geometric relation between sub-apertures

解该方程，可以得到理论上所需的子孔径个数n。实际中，n须为整数，因此取子孔径个数为N = [ n]+1([n]表示向零取整）。

根据三角余弦定理，子孔径的圆心所在圆半径ρ满足：

根据确定的子孔径位置依次设置子孔径自准直平面镜，进行子孔径波前数据的采集。

1.2 子孔径数据去倾斜

子孔径的倾斜误差会对检测结果造成重要影响[15]，为了提高检测精度，在对子孔径数据进行拼接处理前，需要先进行子孔径数据的去倾斜处理，一般采用平面拟合法。

定义z = α x + β y + γ 为笛卡尔坐标系下的一个平面，α、β、γ为平面系数，x和y为采样点对应的坐标。设采集到的子孔径波前数据为W，利用最小二乘法处理子孔径波前数据，拟合得到一个形式为z = α x + β y + γ 的倾斜平面，由此可以获得子孔径波前数据中所具有的倾斜量。将子孔径波前数据与相应的平面值相减可以去除子孔径数据中含有的倾斜量，即去倾斜后的子孔径数据W′为

1.3 子孔径拼接

拼接算法对子孔径拼接检测的效果有重要影响[16]。进行子孔径数据拼接处理时，由于检测过程中子孔径自准直平面镜的旋转和移动，使得两相邻子孔径的重叠区波前数据只能在最小二乘意义下一致。假设获得的两相邻子孔径重叠区域的波前数据分别为和，令，则有：

式中aΔ为z方向的相对平移系数；bΔ为x方向的相对倾斜系数；cΔ为y方向的相对倾斜系数。通过对上式的求解即可得到拼接系数aΔ、bΔ、cΔ。

1.4 重叠区数据的优化

由于两子孔径的重叠区数据即便进行了拼接拟合也不可能完全一致，进行波前重构时可能存在重叠区与两子孔径非重叠区的不平滑过渡，出现不平滑拼接[17]，如图3所示。

图3 子孔径间的不平滑拼接Fig.3 Sub-aperture stitching with saltation

为解决上述问题，可以在波前重构时对重叠区数据进行优化，即利用重叠区采样点的位置为该点的波前数据取值配置权重。采样点与子孔径中心的位置关系如图4所示，O1、O2分别为相邻两子孔径中心，P为两子孔径重叠区的一个采样点，其坐标为，设为波前重构时P点波前数据对应的取值权重，其值由点P与的距离决定，与为两子孔径经过拼接处理后在P点处的波前数据，则优化后P点处的波前数据取值为

优化后的效果如图5所示，重叠区的波前数据经过优化处理可以与两子孔径非重叠区的波前数据平滑过渡，实现相邻子孔径间的平滑拼接。

图4 采样点与子孔径中心的位置关系Fig.4 Relation between sample point and sub-aperture centerr

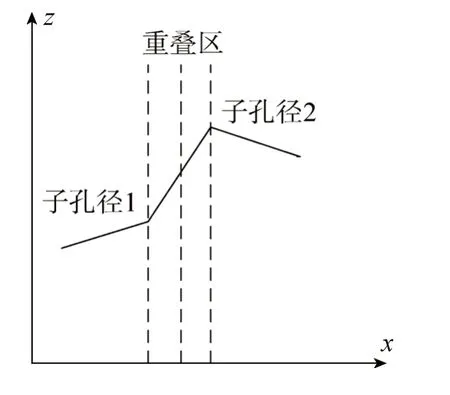
图5 子孔径平滑拼接Fig.5 Sub-aperture stitching without saltation

2 仿真实验

利用ZEMAX软件建立一个口径为3.2m的超大型光学遥感器系统，对该光学系统首先进行全口径波前检测，波前图如图6所示，经计算得到的波前峰谷值（PV值）为0.06015λ（λ为波长），RMS值为0.01293λ。

利用口径为1.8m的自准直平面镜对该光学系统进行子孔径拼接检测。根据子孔径布局原理进行优化计算，可得当子孔径单圈中心对称分布时需要的子孔径个数为7个，子孔径布局如图7所示。

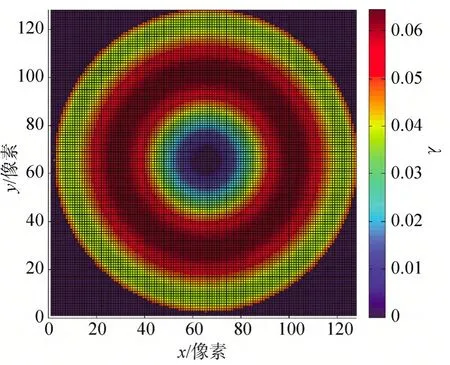
图6 全口径检测得到的波前Fig.6 Wavefront of whole aperture test

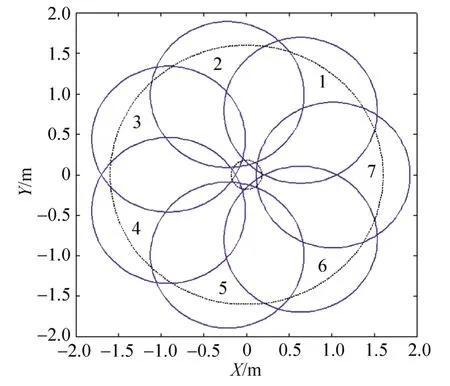
图7 子孔径布局Fig.7 Distribution of sub-apertures

按照确定的子孔径位置，依次设置子孔径自准直镜进行系统检测。在每次进行子孔径自准直镜位置的设定时，都随机加入一定量的倾斜量，分别采集每个子孔径的波前数据。对子孔径波前数据进行去倾斜处理，得到的平面系数α、β、γ见表1。

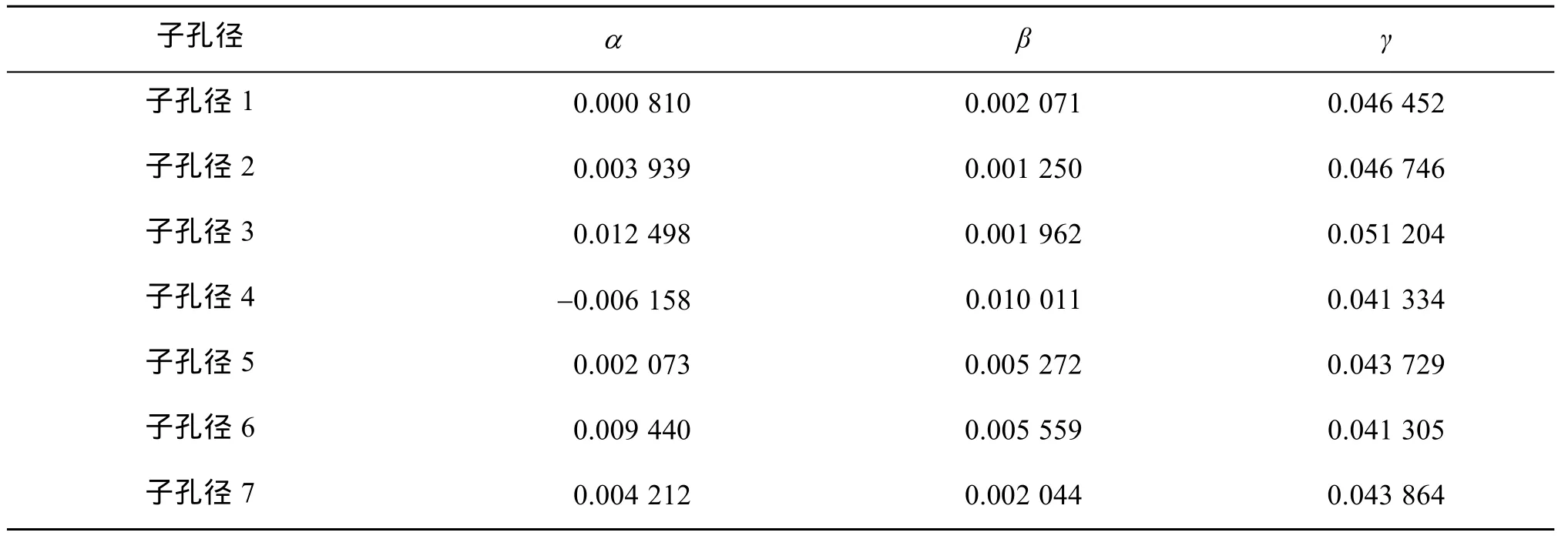
表1 平面系数Tab.1 Plane coefficients

将去倾斜后的数据进行拼接计算，可以得到拼接系数Δa、Δb、Δc，见表2。

进行子孔径平滑拼接就可以得到重构的波前，其PV值为0.06631λ，RMS值为0.01342λ。由于子孔径间的依次拼接会造成误差的积累，故得到的波前数据中含有累积误差。为了消除累积误差的影响，将得到的全口径波前数据进行一次去倾斜处理，得到最终的全口径波前，其PV值为0.06433λ，RMS值为0.01326λ。

表2 拼接系数Tab.2 Stitching coefficients

将子孔径拼接检测结果与全口径检测结果进行对比，见表3，其PV值相差0.00418λ，RMS值相差0.00033λ。可以看出，子孔径拼接检测结果与全口径检测结果相差不大，因此子孔径拼接法检测超大型光学遥感器具有理论可行性。

表3 检测结果比较Tab.3 Comparisonofresults

3 结束语

子孔径拼接法可以实现超大型光学遥感器的系统检测。本文分析了光轴竖直状态下子孔径单圈中心对称分布时，使用子孔径拼接法检测超大型光学遥感器的基本原理，并进行了相关仿真实验。将最终得到的子孔径拼接法检测结果与全口径波前检测法检测结果进行对比，验证了该方法的理论可行性和准确性。未来可以针对子孔径自准直平面镜的机械运动误差、光学加工误差等目前研究中尚未考虑的误差进行仿真分析。

References)

[1]陈晓丽,傅丹鹰.大口径甚高分辨率空间光学遥感器技术途径探讨[J].航天返回与遥感,2003,24(4):19-24.CHEN Xiaoli, FU Danying. Solutions for Space Optical Remote Sensor with Large Aperture and Ultrahigh Resolution[J].Spacecraft Recovery Remote Sensing, 2003, 24(4): 19-24. (in Chinese)

[2]胡君,王栋,孙天宇.现代航天光学成像遥感器的应用与发展[J].中国光学与应用光学,2010,3(6):519-533.HU Jun, WANG Dong, SUN Tianyu. Application and Development of Recent Space Optical Imaging Remote Sensors[J].Chinese Journal of Optics and Applied Optics, 2010, 3(6): 519-533. (in Chinese)

[3]岳涛,李博,陈晓丽,等.空间光学发展现状和未来发展[J].航天返回与遥感,2011,32(5):1-9.YUE Tao, LI Bo, CHEN Xiaoli, etal. The Current and Future Development of Space Optics[J]. Spacecraft Recovery Remote Sensing, 2011, 32(5): 1-9. (in Chinese)

[4]刘智颖,张磊,胡原.子孔径拼接技术应用的研究[J].应用光学,2008,29(6):1009-1012.LIU Zhiying, ZHANG Lei, HU Yuan. Application of Sub-aperture Stitching Technique[J]. Journal of Applied Optics, 2008,29(6): 1009-1012. (in Chinese)

[5]闫力松,王孝坤,罗霄,等.基于非理想标准镜的子孔径拼接干涉检测技术研究[J].红外与激光工程,2014,43(1):178-183.YAN Lisong, WANG Xiaokun, LUO Xiao, etal. Sub-aperture Stitching Interferometry Based on Non-ideal Standard Mirror[J].Infrared and Laser Engineering, 2014, 43(1): 178-183. (in Chinese)

[6]苏云,李博.子孔径拼接检测方法的目标函数优化[J].航天返回与遥感,2008,29(1):55-58.SU Yun, LI Bo. Optimizing the Object Function in Sub-aperture Stitching[J]. Spacecraft Recovery Remote Sensing, 2008,29(1): 55-58. (in Chinese)

[7]侯溪,伍凡,杨力,等.子孔径拼接干涉测试技术现状及发展趋势[J].光学与光电技术,2005,3(3):50-53.HOU Xi, WU Fan, YANG Li, etal. Status and Development Trend of Sub-aperture Stitching Interferometric Testing Technique[J]. Optics Optoelectronic Technology, 2005, 3(3): 50-53. (in Chinese)

[8]Michael B. Stitching Interferometer for Large Plano Optics Using a Standard Interferometer[J]. Proc. of SPIE, 1997, 3134:39-50.

[9]Jon F, Paul D, Paul E M, etal. An Automated Sub-aperture Stitching Interferometer Workstation for Spherical and Aspherical Surfaces[J]. Proc. of SPIE, 2003, 5188: 296-307.

[10]Andrew K, Paul M, Michael D. Measurement of High-departure Aspheres Using Sub-aperture Stitching with the Variable Optical Null[J]. Proc. of SPIE, 2010, 7655: 121-124.

[11]郭红卫,陈明仪.圆柱坐标下多孔径扫描拼接技术的迭代方法[J].光学学报,2000,20(8):1047-1052.GUO Hongwei, CHEN Mingyi. An Iterative Algorithm of Multi-aperture Transformation and Connection Technique in Cylindrical Coordinates[J]. Acta Optical Sinica, 2000, 20(8): 1047-1052. (in Chinese)

[12]程刚,蒋世磊.大口径光学件误差均化拼接技术[J].光电工程,2006,33(6):118-129.CHENG Gang, JIANG Shilei. Large Aperture Optical Components of Stitching Technique by Error Averaging[J].Opto-Electronic Engineering, 2006, 33(6): 118-129. (in Chinese)

[13]闫力松,王孝坤,郑立功,等.大口径反射镜子孔径拼接自检验精度分析[J].红外与激光工程,2014,43(6):1920-1924.YAN Lisong, WANG Xiaokun, ZHENG Ligong, etal. Large-diameter Mirror Stitching Accuracy Analysis Based on Self-test[J]. Infrared and Laser Engineering, 2014, 43(6): 1920-1924. (in Chinese)

[14]李新南,张明意.大口径光学平面的子孔径拼接检验研究[J].光学技术,2006,32(4):514-517.LI Xinnan, ZHANG Mingyi. Study on the Sub-aperture Stitching Interferometry for Large Plano-optics[J]. Optical Technique, 2006, 32(4): 514-517. (in Chinese)

[15]张蓉竹,杨春林,许乔,等.子孔径拼接干涉检测中去倾斜处理技术[J].强激光与粒子束,2004,16(7):879-882.ZHANG Rongzhu, YANG Chunlin, XU Qiao, etal. Anti-tilting Technology of the Sub-aperture Stitching Interferograms[J].High Power Laser and Particle Beams, 2004, 16(7): 879-882. (in Chinese)

[16]丁凌艳,戴一帆,陈善勇.平面子孔径拼接测量研究[J].光学精密工程,2008,16(6):978-985.DING Lingyan, DAI Yifan, CHEN Shanyong. Experiments of Sub-aperture Stitching Interferometry for Flat Mirrors[J]. Optics and Precision Engineering, 2008, 16(6): 978-985. (in Chinese)

[17]闫公敬,张宪忠,李柱.子孔径拼接检测光学平面反射镜技术[J].红外与激光工程,2014,43(7):2180-2184.YAN Gongjing, ZHANG Xianzhong, LI Zhu. Technology of Sub-aperture Stitching Testing Optical Flat Mirror[J]. Infrared and Laser Engineering, 2014, 43(7): 2180-2184. (in Chinese)