多视场遥感图像虚拟焦面拼接理论误差分析

岳春宇 何红艳 鲍云飞 邢坤 周楠

（北京空间机电研究所，北京100094）

0 引言

随着遥感对地观测技术的发展，国土调查、地图测绘等应用领域对增大遥感图像覆盖范围的要求不断提高，因此，扩大视场、获得大宽幅数据是空间光学遥感发展的一个重要方向。由于空间相机受卫星平台、空间环境等因素制约，以及CCD器件工艺的限制[1]，一般采用多相机多视场图像拼接的方式来获取满足较高空间分辨率且大幅宽的图像[2]。在遥感应用领域，目前遥感图像拼接主要是通过图像匹配，寻找同名信息建立图像间的空间对应关系，建立空间转换模型，再将遥感图像转换到同一坐标系下[3-5]。这种拼接方式需要在待拼接图像中找到同名信息，当待拼接图像重叠区域提取同名特征困难时，则无法准确拼接[6]。而且这种方法计算量大，不同的待拼接图像处理结果不同，不具有普遍性，不能够实现标准化生产。数据生产单位更希望通过成像几何关系直接对不同相机图像进行拼接，这样避免了复杂费时的图像匹配，同时可以按照统一流程高效生产图像数据产品。

本文从遥感图像虚拟焦面拼接原理出发，推导图像拼接理论误差公式，研究影响多视场遥感图像拼接精度的因素，并通过仿真实验对图像拼接误差进行分析。

1 多视场遥感图像拼接

多视场遥感图像拼接需要建立数学转换模型，将不同相机图像通过坐标转换以及重采样，变换到拼接图像坐标系下。在常规遥感图像产品生产过程中，地面点坐标转换到图像坐标系下，需要经过多次坐标转换。

1.1 多视场遥感图像拼接空间坐标系确定

地面点P由物方坐标计算其图像坐标的流程为[7]：

1）根据成像时刻，从星历文件中获得的卫星位置及速度矢量参数，计算地心直角坐标系到卫星轨道坐标系的变换矩阵，将P点物方坐标转换到卫星轨道坐标系下，得到P点在成像时所对应的卫星轨道坐标系坐标；

2）根据成像时刻星历记载的成像时卫星姿态参数，计算卫星轨道坐标系与卫星本体坐标系间的正交变换矩阵，将P点的卫星轨道坐标系坐标转换到卫星本体坐标系，得到P点在卫星本体坐标下坐标；

3）根据相机安置矩阵，得到从卫星本体坐标系到像空间坐标系的正交变换矩阵，将P点卫星本体坐标转换到相机坐标系下，得到P点的像空间坐标；

4）根据摄影比例尺，将P点的像空间坐标投影到像平面坐标，即得到地面点P的图像坐标。

在上述转换过程中，第1、2步只与卫星平台有关，坐标转换关系适用于待拼接的各台相机；第3、4步是相机与卫星本体和相机内部之间的坐标转换。在建立成像几何模型时，由于待拼接各台相机第 3、4步中的坐标转换矩阵不同，所以本文在讨论多视场遥感图像拼接误差时，将成像几何模型简化为由共线条件方程表示的卫星本体坐标系到像空间坐标的转换过程。

为了方便后续讨论，不考虑轨道坐标系与地心坐标系之间的转换。对于两台相机拼接的情况（如图1所示），将各相机摄影中心、地面点统一到一个物方坐标系(O - XYZ)中，将各图像统一到一个像空间坐标系(O - x yz)中，则物方坐标和图像坐标就在两个坐标系下转换，满足经典摄影测量共线方程的条件。(O - XYZ)与(O - xyz)的原点重合，为左右摄影中心 SL及 SR的中点，Y轴与y轴指向飞行方向，Z轴与z轴指向地心相反方向，X轴与x轴分别垂直于YOZ与yOz平面，并构成右手坐标系。

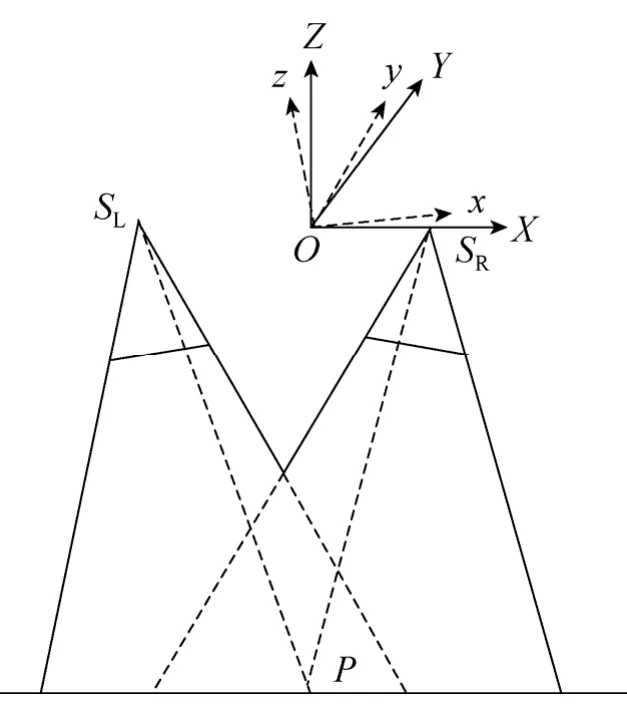
图1 图像拼接坐标系Fig.1 Imagemosaiccoordinatesystem

1.2 多视场遥感图像拼接原理

为方便讨论，本文以两幅图像拼接为例进行研究分析。对于同一地面点P(X,Y,Z)，在两幅图像上的图像坐标由共线方程计算得到[8]：

式中 (xL, yL)与(xR,yR)分别为地面点P在左右图像像空间坐标系下坐标； fL、 fR为左右图像摄影主距。在以虚拟摄影中心为原点的像空间辅助坐标系中，他们的空间坐标分别为和分别为左右图像的摄影中心物方坐标；分别为左右图像外方位角元素的方向余弦参数，构成的旋转矩阵为：此时地面点P和左右图像的摄影中心在同一物方坐标系下。

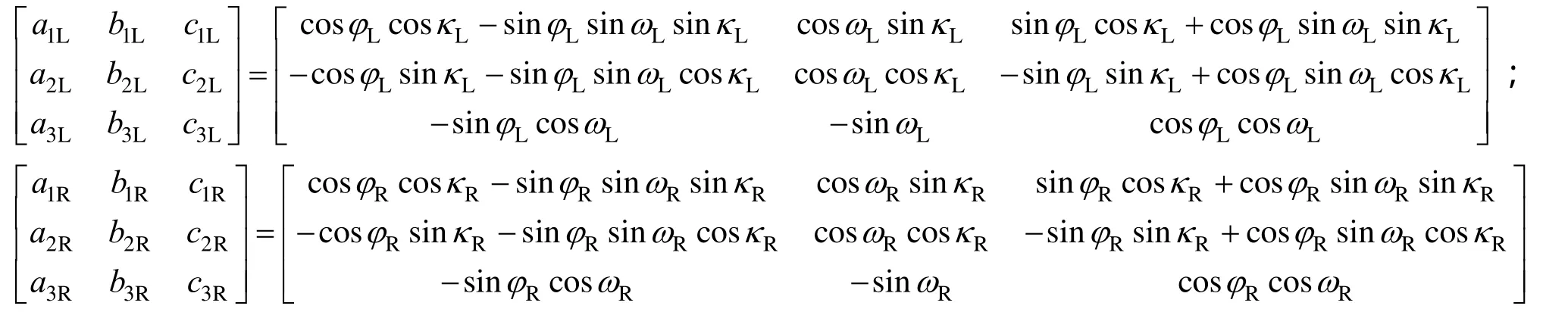
所有左右图像上的点由共线方程投影到像空间坐标系中的过 ( 0,0,- fM)点且平行于平面xOy的平面上，即得到了虚拟拼接图像。与作为地面点P在左右图像中的同名点，投影到像空间坐标系中的高程为 - fM的平面上，图像坐标的差异即是拼接误差。

2 多视场遥感图像拼接误差

2.1 基于像方的图像拼接误差

基于像方的拼接方案就是将待拼接不同图像所在的像空间坐标系坐标投影到虚拟拼接图像焦面上。首先建立虚拟拼接图像坐标系，一般原点为摄影基线中点，然后找到待拼接图像像空间坐标系与虚拟拼接图像坐标系之间的转换关系，最后将待拼接图像所有像素坐标投影到虚拟拼接图像焦面上。

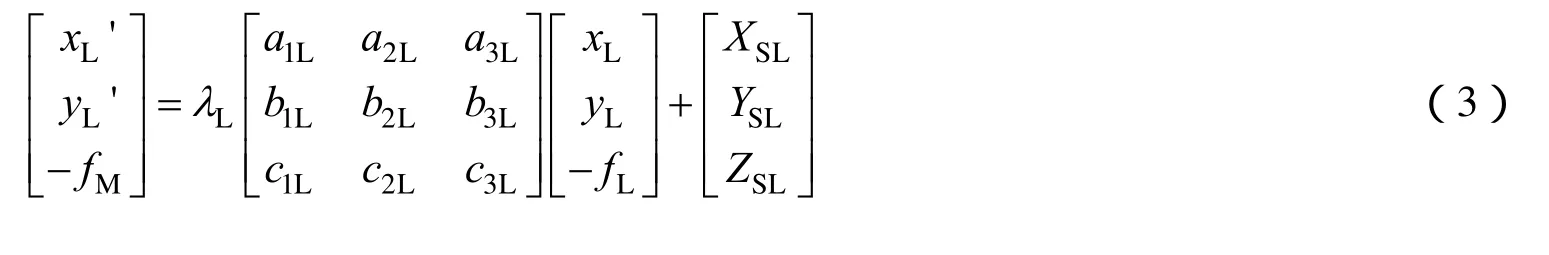
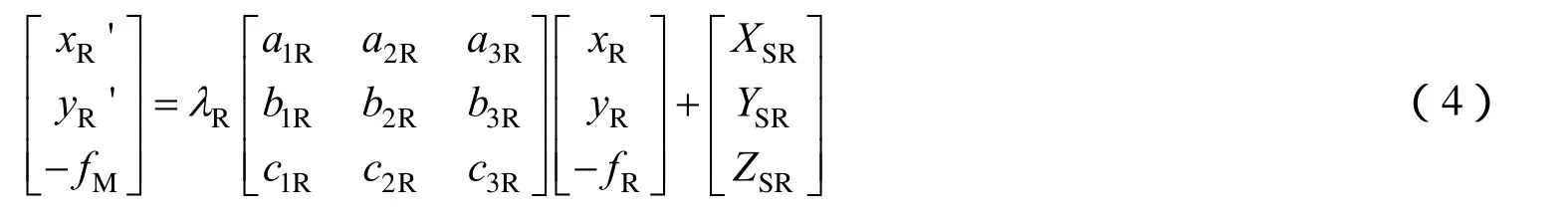
式中Lλ与Rλ分别为左右图像的摄影比例尺，消除摄影比例尺，整理得：

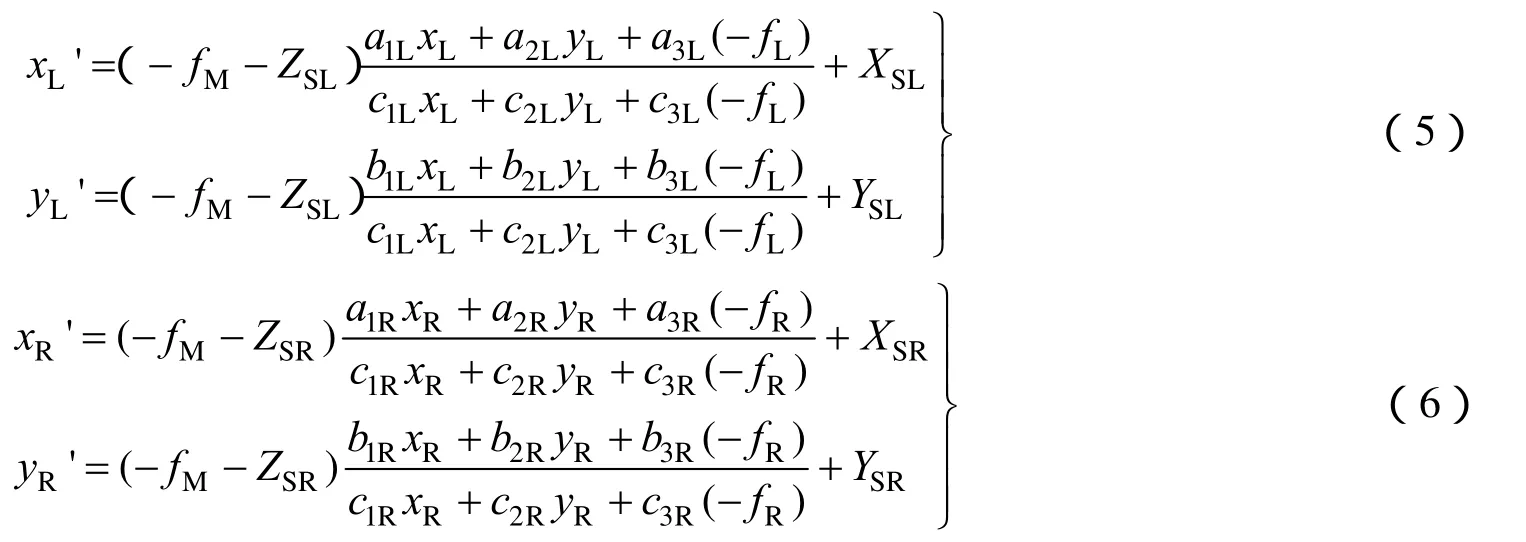
将式（1）、（2）带入式（5）、（6）得，

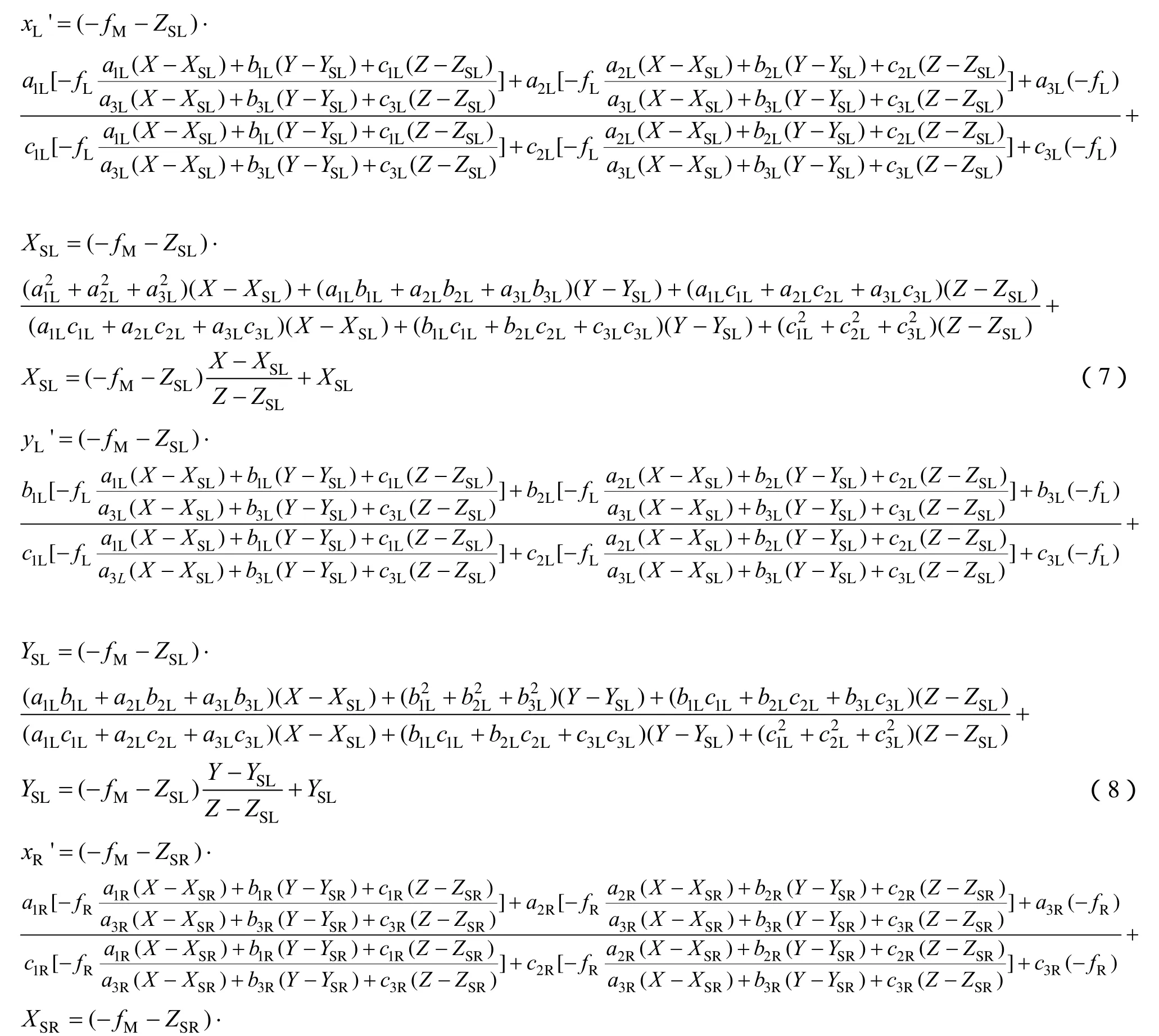
将左右图像的坐标归化到虚拟拼接图像坐标，才可以进行比较。由于左右图像的像主点在虚拟拼接图像中的坐标分别为和，所以与在虚拟拼接图像中满足多视场遥感图像像方拼接在x方向上误差，在y方向上误差

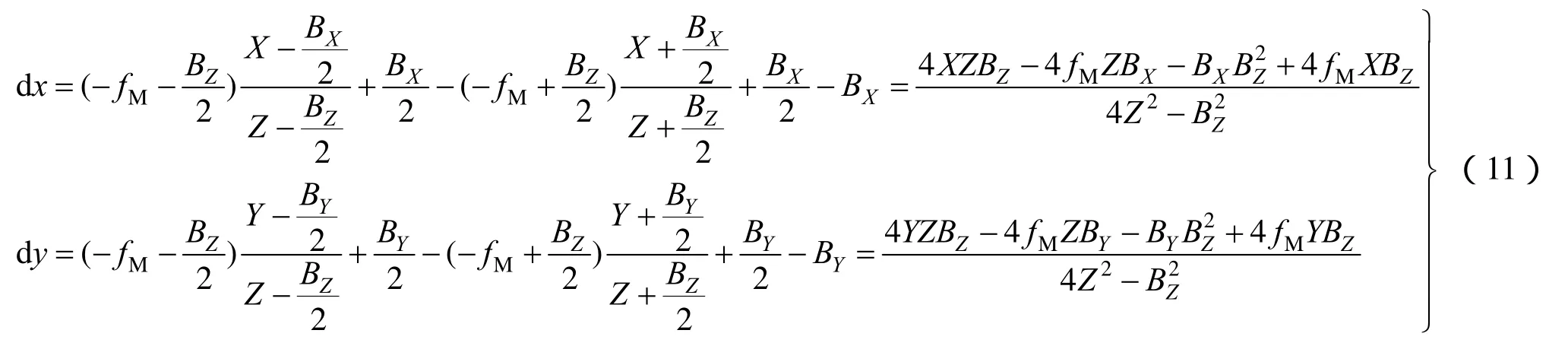
从式（11）可以看出，像方拼接图像的误差源为地面点坐标、摄影基线及虚拟拼接图像主距，在投影到虚拟像平面时，当待拼接图像主距与虚拟图像主距相等的情况下，相机的姿态角及主距不产生拼接误差。考虑到实际成像时一般垂直摄影，两台相机摄影中心没有高差，可以认为摄影基线B在Z方向上的分量此时基于像方的图像拼接误差为，

2.2 基于物方的图像拼接误差

生产单位一般采用基于物方的图像拼接。基于物方的拼接方案首先将待拼接图像投影到物方的某一高程面上，一般为覆盖地区的平均高程，即给定物方投影面的坐标 ZM，再由物方坐标(X ,Y,ZM)根据待拼接图像的严格成像模型计算其在图像中的图像坐标与，重采样原始图像，即得到系统几何校正图像，最后根据系统几何校正后图像像素的地理坐标进行图像拼接。

考虑到图像坐标系与物方坐标系之间的转换关系，此时

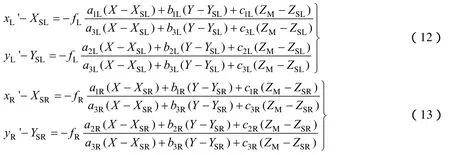
考虑到实际成像时一般垂直摄影，卫星没有俯仰、偏航和侧摆。令为左右摄影中心连线的中点，摄影基线为，为了计算方便，令即待拼接的两台相机摄影时摄影中心高程值相同。此时式（12）、（13）简化为

基于物方的拼接只进行了一次投影变换，多视场遥感图像像方拼接在x方向上误差在y方向上误差

从上式可以看出，基于物方拼接图像的误差源为摄影基线、拼接图像主距及物方投影高程。当待拼接相机垂直成像且无侧摆时，且待拼接图像主距与虚拟图像主距相等的情况下，基于物方的图像拼接误差大小与基于像方的拼接方法相同。

3 仿真实验及分析

根据上述理论推导及分析，采用仿真数据实验，对图像拼接误差进行仿真实验分析。设定两台框幅式遥感相机，摄影基线垂直于飞行方向的分量为0.2m，即摄影基线X方向上的分量 BX= 0 .2m，摄影基线平行于飞行方向的分量为0.01m，即摄影基线Y方向上的分量 BY= 0 .01m，BX、BY是相机安装前后不对齐造成的。仿真实验中模仿待拼接的两台相机的摄影中心连线垂直于飞行方向，安装时有0.01m的误差，物方空间坐标系下左右摄影中心坐标分别为，，地面点P物方坐标，基于像方拼接的虚拟拼接图像主距Mf=2000mm，垂直摄影情况下航高 500H= km，即摄影比例尺为1∶250000，焦面CCD像元数为60000×60000个，像元分辨率为2.5m，图像重叠区为4000个像元，基于物方拼接的物方投影高程为50m，则投影面MZ =–499950m，相机安装侧摆角为0°，CCD尺寸为10μm×10μm。选择平面坐标分布均匀地面点，在高程不同时，同名点在基于像方拼接图像上的坐标差异由式（11）计算，计算结果见表1和表2。同名点在基于物方拼接图像上的坐标差异由式（16）计算，计算结果为dx=8.0×10–7m=0.08像元，dy=0.4×10–7m=0.004像元。

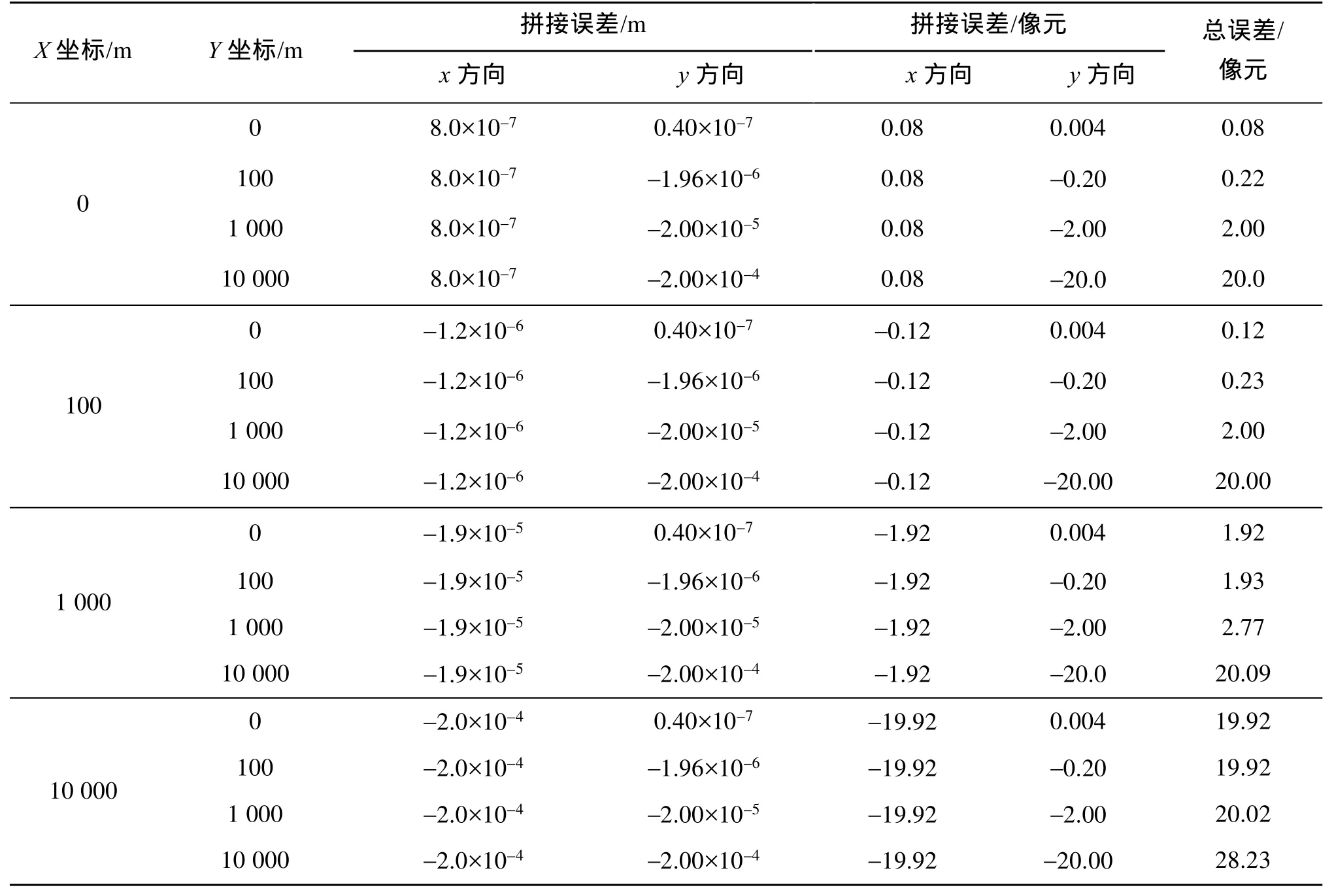
表1 高程为100m时地面点位置对基于像方拼接误差的影响Tab.1 Influences of ground point position on virtual image geometric mosaic error with elevation value 100m

实验中选择16个地面点（见表1和表2），在高程分别为100m和1000m时的32种情况下来分析基于像方拼接的理论误差。由于基于像方拼接直接将待拼接图像坐标投影到虚拟拼接图像焦面上，地面点高程的影响较小。随着地面点在拼接区内远离虚拟拼接图像主点，拼接误差增大；x方向与y方向的拼接误差变化规律一致。当地面坐标中X或Y偏离拼接物方坐标系原点100m（即40个像元）时，拼接误差为0.2个像元左右，可以直接根据两幅图像成像几何模型计算同一地面点的像点坐标进行拼接。当地面坐标X或Y偏离物方坐标系原点1000m（即400个像元）时，拼接误差为3个像元左右，不能对待拼接图像进行直接拼接。当地面坐标X或Y偏离物方坐标系原点10000m（即4000个像元）时，拼接误差已达到20像元左右。随着地面坐标的变化，其在待拼接图像中对应的同名点投影到虚拟拼接图像焦面上的坐标也变化，且主要与地面点平面位置变化有关。一般图像间重叠区域为100个像元，即百米级，此时拼接误差不超过1个像元，所以当待拼接图像成像几何模型稳定，经过系统几何校正消除系统误差后，可以将同名点根据成像几何模型投影到虚拟图像中直接拼接。当严格检校出摄影基线B后，可以根据式（11）计算待拼接图像中同名点在虚拟拼接图像中的拼接误差值，进而对拼接区重叠像元数设计提供参考。

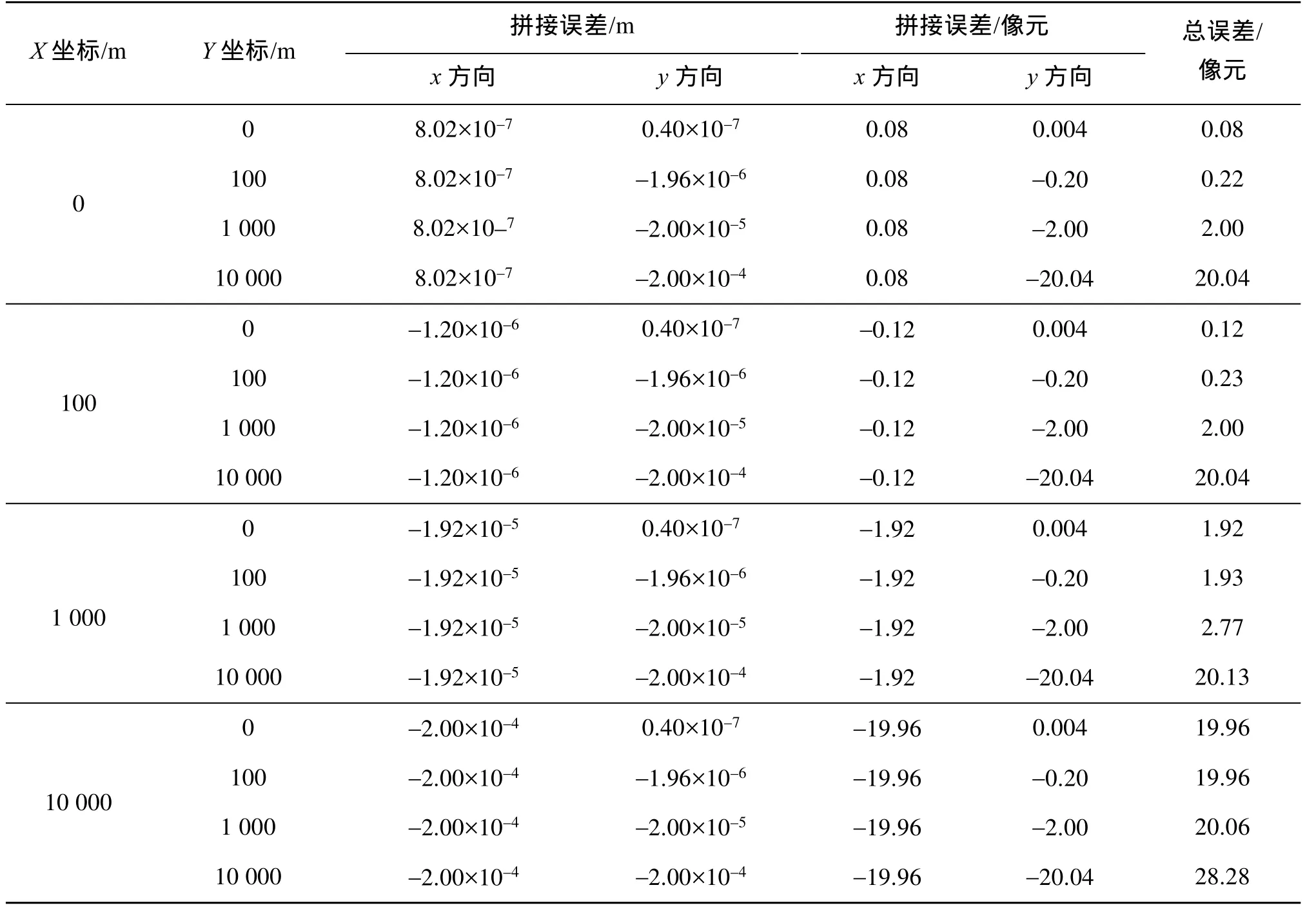
表2 高程为1000m时地面点位置对基于像方拼接误差的影响Tab.2 Influences of ground point position on virtual image geometric mosaic error with elevation value 1 000m

通过仿真实验分析得出，当垂直摄影且待拼接图像主距等于虚拟拼接图像主距时，在重叠区为100个像元左右的情况下，如果成像几何模型稳定，基于像方和物方的拼接方法拼接误差都不到1个像元，且拼接误差具有系统性，通过拼接理论误差推导，可以计算基于像方及物方的拼接方法拼接理论误差，经过系统误差校正，可以大幅降低，不影响目视判读。

4 结束语

本文由严格共线方程几何定位模型推导了不同视场图像基于虚拟焦面的拼接误差。拼接图像可以通过将待拼接图像投影到虚拟像平面或物方高程面获得。将待拼接图像投影到虚拟像平面的基于像方的拼接方法，需要将待拼接图像投影后坐标，转换到虚拟像平面所在的图像坐标系下。拼接误差主要受地面点坐标、摄影基线及虚拟拼接图像主距影响，当待拼接图像主距与虚拟图像主距相等的情况下，待拼接图像的姿态角及主距不产生拼接误差。将待拼接图像投影到物方高程面的基于物方的拼接方法直接给定地面点高程，计算地面点在虚拟拼接图像中的图像坐标进行拼接，拼接误差主要受摄影基线、待拼接图像主距及物方投影高程面影响。

基于物方的图像拼接方法，待拼接图像中的同名点投影到固定高程面上，在不考虑俯仰、翻滚及侧摆的影响时，拼接误差是一个系统值，仅与摄影基线、虚拟拼接图像主距和虚拟投影高程面有关，这三个因素都可以进行地面标定。仿真结果显示，基于物方的图像拼接方法误差较小，在模型稳定的情况下，可以直接根据成像几何模型计算待拼接图像的像点坐标在虚拟拼接图像中的坐标位置，进行图像拼接。下一步的研究应重点关注相机几何定位模型误差及相机状态变化时对拼接误差的影响，以及对不同地区真实遥感图像进行实验分析对理论进行验证。

References)

[1]杜延峰.一种新型大面阵CCD航测相机等效中心投影影像生成技术研究[D].西安:长安大学,2010.DU Yanfeng. Study on Equivalent Center Projection Image Generation Technology on a New Large Array CCD Aerial Camera[D]. Xi’an: Chang’an University, 2010. (in Chinese)

[2]白照广.高分一号卫星的技术特点[J].中国航天,2013,8:5-9.BAI Zhaoguang. GF-1 Satellite Technique Characteristics[J]. Aerospace China, 2013, 8: 5-9. (in Chinese)

[3]HUA Shungang, ZENG Lingyi, OU Zongying. Fast Algorithm for Cylindrical Panoramic Image Mosaic[J]. Journal of Data Acquisition＆Processing, 2006, 21(4): 434-438.

[4]ZHANG Jing, HU Zhiping, LIU Zhitai. Image Automatic Mosaics Based on Contour Phase Correlation[J]. Frontiers of Mechanical Engineering in China. 2007, 2(2): 228-234.

[5]周清华,潘俊,李德仁.遥感图像镶嵌接缝线自动生成方法综述[J].国土资源与遥感,2013,25(2):1-7.ZHOU Qinghua, PAN Jun, LI Deren. Overview of Automatic Generation of Mosaicking Seamlines for Remote Sensing Images[J]. Remote Sensing For Land Resources, 2013, 25(2): 1-7. (in Chinese)

[6]岳春宇,郑永超,陶宇亮.星载激光测高仪辅助卫星摄影测量浅析[J].航天返回与遥感,2013,34(4):71-76.YUE Chunyu, ZHENG Yongchao, TAO Yuliang. Study on Space-borne Laser Altimeter Supported Satellite Photogrammetry[J]. Spacecraft Recovery Remote Sensing, 2013, 34(4): 71-76. (in Chinese)

[7]张过.缺少控制点的高分辨率卫星遥感影像几何纠正[D].武汉:武汉大学,2005.ZHANG Guo. Rectification for High Resolution Remote Sensing Image Under Lack of Ground Control Points[D]. Wuhan: Wuhan University, 2005. (in Chinese)

[8]余俊鹏.高分辨率卫星遥感影像的精确几何定位[D].武汉:武汉大学,2009.YU Junpeng. Accurate Geometric Positioning of High Resolution Satellite Remote Sensing Imagery[D]. Wuhan: Wuhan University, 2009. (in Chinese)

[9]高颖慧,沈振康.航空摇摆图像组的配准拼接算法[J].红外与激光工程,2009,38(1):170-174.GAO Yinghui, SHEN Zhenkang. Registration and Stitching Algorithm for Aviation Swaying Image Set[J]. Infrared and Laser Engineering, 2009, 38(1): 170-174. (in Chinese)

[10]王慧,吴云东,张永生.面阵CCD数字航测相机影像几何拼接误差模型与分析[J].测绘学院学报,2003,20(4):257-262.WANG Hui, WU Yundong, ZHANG Yongsheng. Modeling and Analyzing of Geometric Joint Error for CCD Matrix Images of Digital Aerial Camera[J]. Journal of Institute of Surveying and Mapping, 2003, 20(4): 257-262. (in Chinese)

[11]王慧.面阵CCD航测相机成像模型与处理技术[D].郑州:解放军信息工程大学,2006.WANG Hui. Imaging Model and Processing of Large Format CCD Aerial Camera[D]. Zhengzhou: PLA University of Information Engineering, 2006. (in Chinese)

[12]徐彭梅,杨桦,伏瑞敏,等.CBERS-1卫星CCD相机的光学拼接、配准和定焦[J].航天返回与遥感,2001,22(3):12-15.XU Pengmei, YANG Hua, FU Ruimin, etal. Optical Butting, Registration and Focus-fixing of CCD Camera for CBERS-1 Satellite[J]. Spacecraft Recovery Remote Sensing, 2001, 22(3): 12-15. (in Chinese)

[13]温红艳.遥感图像拼接算法研究[D].武汉:华中科技大学,2009.WEN Hongyan. Study on Remote Sensing Images Mosaic[D] Wuhan: Huazhong University of Science and Technology, 2009. (in Chinese)

[14]阮鹏.多图像拼接算法研究[D].长沙:中南大学,2009.RUANPeng.Studyon Images Mosaic[D].Changsha:Zhongnan University,2009.(inChinese)

[15]严磊.基于特征匹配的全自动图像拼接算法研究[D].合肥:中国科学技术大学,2009.YAN Lei. Automatic Image Mosaic Method Based on Feature Matching[D]. Hefei: University of Science and Technology of China, 2009. (in Chinese)